Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2651. |
A candle is placed in front of a concave lens. a. Draw the course of the light ray through lens and study the nature of the image formed. b. If it possible for the concave lens to form a real image ? c. If possible draw the corresponding ray diagram. |
Answer» Solution :a. 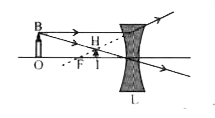 b. YES. Whith incident BEAM HIGHLY CONVERGING . 
|
|
| 2652. |
Derive the expression for the torque tau acting ona rectangular current loop of area A placed in a uniform magnetic field B. Show thatvec tau=vecmxx vec B where vecm is the moment of the current loop given by vecm =vecIA. |
Answer» Solution :Consider a rectangular coil PQRSsuspended in a uniform magnetic field `vecB`, with its axis perpendicular to the field.  Let `I=` current flowing through the coil PQRS `a,b=` sides of the coil PQRS ` A= ab= `AREA of the coil. ` theta =` angle between the direction of `vecB` and normal to the plane of the coil. According to Fleming's left hand rule, the magnetic forces on sides PS and QR are equal, OPPOSITE and collinear (along the axis of the loop), so their resultant is zero. The side PQ experiences a normal inward force equal to lbB while the side RS experiences an equal normal outward force. These two forces form a couple which exerts a troque given by. ` tau=` force x perpendicular distance `=lbBxx asin theta =lBA sin theta` If the rectangular loop has N turns, the torque increases N times i.e., `vec tau =NIBA sin theta` But `NIA =m`, the magnetic moment of the loop , so ` tau =mB sin theta` In vector NOTATION, the torque`vectau` is given by ` vectau=vecmxx vecB`. |
|
| 2653. |
In Young.s double slit experiment with monochromatic source of light of wavelength 6000 A^(2), if the path difference at a point on the screen is 6xx 10^(-6)m, the number of the bright band formed at that point is |
| Answer» ANSWER :D | |
| 2654. |
The energy required to establish a current of 4A in a self-inductance of L = 200mH is: |
|
Answer» 0.16J |
|
| 2655. |
A conducting wire of 100 turns is wound over and near the centre of a solenoid of 100cm length and 2cm radius having 1000 turns. Calculate the mutual induction of the two coils. |
| Answer» SOLUTION :`157.75muH` | |
| 2656. |
In a silicon transistor a change of 7.89 mA in the emitter current produces a change of 7.8 mA in the collector current . What is the change in the base current necessary to produce an equivalent change in the collector current ? |
| Answer» SOLUTION :`89.94 MU A` | |
| 2657. |
What are the characteristics to be taken care of while doping a semiconductor? Justify your answer. |
|
Answer» Solution :(a) The SIZE of the dopent atom should be such that it do not distort the pure semiconductor labtice. (b) It can easily contribute a CHARGE CARRIER on FORMING covalent bond withh pere Si or Ge. |
|
| 2659. |
A proton and an alpha=particle are accelerated using the same potential difference.How are the de-Broglie wavelengths lambda_(p) and lambda_(a) related to each other? |
|
Answer» Solution :ACCORDING to FORMULA ,`lambda=(h)/(p)=(1)/(sqrt(2mK))=(1)/(sqrt(2Vqm))` Here V is same and so, `therefore (lambda_(p))/(lambda_(a))=sqrt((q_(ALPHA)m_(alpha))/(q_(p)m_(p)))=sqrt(((2e)(4m_(p)))/((E)(m_(p))))=sqrt(8)=2sqrt(2)` |
|
| 2660. |
Calculate the binding energy per nucleon for a ._(6)C^(12) nucleus. Atomic mass of._(6)C^(12) = 12am u, mass of a photon = 1.007825 amu, mass of a neutron = 1.008665 amu. |
|
Answer» |
|
| 2661. |
Two slits in Young's double slit experiment are illuminated by two different lamps emitting light of the same wavelength will you observe the interference pattern ? |
| Answer» Solution :No, The light waves EMITTED by two different lamps cannot be coherent . So, the condition of maxima and MINIMA of INTENSITY will RAPIDLY on the screen, producing UNIFORM illumination. | |
| 2662. |
Obtain the relation between magnetisation overset(to)((m) ) and magnetic intensity overset(to) ((H)) for a solenoid. |
|
Answer» Solution :Consider a long solenoid of n turns per UNIT length and CARRYING a current I. The magnetic field in the interior of the solenoid `overset(to) (B_0) = mu_(0) nI ""…(1)` If the interior of the solenoid is filled with a material with non-zero magnetization, the field inside the solenoid will be greater than `overset(to) (B_0)`. The net `overset(to) (B) ` field in the interior of the solenoid may be expressed as, `overset(to) (B) = overset(to)(B_0) + overset(to) (B_m) ""...(2)` where `overset(to) (B_m)` is the field contributed by the material core. It turns out that this additional field `B_m` is proportional to the magnetisation `overset(to) (M)` of the material and is expressed as `overset(to) (B_m) prop overset(to) (M)` `overset(to) (B_m) = mu_(0) overset(to) (M) ""...(3)` where `mu_0` is same CONSTANT (permeability of vacuum) that appear in Biot-Savart.s law. It is convenient to introduce another vector field H called the magnetic intensity which is defined by, `overset(to) (H) = (overset(to) (B) )/( mu_0) - overset(to) (M) ""...(4)` where `overset(to) (H)` has the same dimension as `overset(to) (M)` and is measured in units of `Am^(-1)`. Thus, the total magnetic field `overset(to) (B)` is written as, `overset(to) (B) = mu_(0) ( overset(to) (H) + overset(to) (M) )""...(5)` The total magnetic field inside the sample is DIVIDED into two PARTS : (1) Due to external factors such as the current `overset(to) (H)` in the solenoid. (2) The other is due to the specific nature of the magnetic material namely `overset(to) (M)`. |
|
| 2663. |
A uniform tube of length 60.5 cm is held vertically with its lower end dipped in water. A sound source of frequency 500 Hz sends sound a waves into the tube. When the length of tube above water is 16cm and again when it is 50cm, the tube resonates with the source of sound . Two lowest frequencies to which tube will resonate when it is taken out of water are, |
|
Answer» 281562 |
|
| 2664. |
If L=20.04 m pm 20.01 m B= 2.52 m pm 0.02 m What are the values of (LxxB)and ( L/B) ? |
|
Answer» Solution :Given errors are ABSOLUTE erors, while the rule SAYS that PERCENTAGE error x are to be added. Hence, the first STEP will be to convert the given absolute errosinto percentage errors. `L= 20.04 m PM (0.01)/(20.04) xx10% = 20.04m pm 0.05 %` `B = 2.52 m pm (0.02)/(2.52)xx100% = 2.52 m pm 0.79 % ` |
|
| 2665. |
If l_1 and l_2are the lengths of air column for the first and second resonance when a tuning fork of frequency n is sounded on a resonance tube, then the distance of the displacement antinode from the top end of the resonance tube is, |
|
Answer» `2(l_1 - l_1)` |
|
| 2666. |
In which case is the power being delivered by a given progressive sinusoidal wave on a given string is doubled? Material of the string is unchanged. |
|
Answer» The wave amplitude is doubled (keeping the frequency the same). |
|
| 2667. |
Two concentric rings placed in a gravity free region in yz-plane one of radius R carries a + Q and second of radius 4R and charge –8Q distributed uniformly over it. Find the velocity with which a point charge of mass m and charge +q should be projected from a a distance 3R from the centre of rings on its axis so that it will reach to the centre of the rings. |
|
Answer» `K_i+U_i=K_f+U_f` `or 1/2mv^2+(+Q)V_i=0(+q)V_f` or `v=sqrt((2q)/m(-V_i+V_f))` `sqrt((2a)/m[(-Q)/(sqrt(10)R)+(8Q)/(5R)+Q/R-(8Q)/(4R)] 1/(4piepsilon_0))` `=sqrt((Qq)/(2piepsilon_0mR) ((3sqrt(10)-5)/(5sqrt10)))` |
|
| 2668. |
A de source of emf E_1 = 100 V and internal resistance r =0.5 Omega ,a storage battery of emf E_2 =90 V and an external resistance R are connected as shown in figure. For what value of R no current will pass through the battery ? |
|
Answer» `5.5Omega ` |
|
| 2669. |
A: l amu = 931.48 MeV R: The statement follows the E = mc^(2) equation. |
|
Answer» Both ASSERTION and REASON are TRUE and the reason is CORRECT EXPLANATION of the assertion. |
|
| 2670. |
Find the velocity of image in the shown below |
|
Answer» SOLUTION :`n_(2)/v-n_(1)/u=(n_(2)-n_(1))/R` `RARR n_(2)/v=(n_(2)-n_(1))/R+n_(1)/u` `rArr n_(2)/v=((n_(2)-n_(1))u+n_(1)R)/(R u)` `rArr v=(n_(2) Ru)/((n_(2)-n_(1))u+n_(1)R)=90` cm `n_(2)/v-n_(1)/u=(n_(2)-n_(1))/R` |
|
| 2671. |
Four particles of masses 5kg,3kg,2kg and 4kg are placed in the X-Y plane at the points A (1,6), B(-1,5), C(2,-3) ,D(-1,-4)respectively. the coordinates of CoM are |
|
Answer» |
|
| 2672. |
A radioactive substance X decays into another radioactive substance Y. Initially only X was present. lamda_(x) and lamda_(y), are the disintegration constants of X and Y. N_(x) and N_yare the number of nuclei of X and Y at any time t. Number of nuclei N_ywill be maximum when |
|
Answer» `(N_y)/(N_(X)-N_(y))=(lamda_(y))/(lamda_(x)-lamda_y)` |
|
| 2673. |
In a Young'sdouble slit experiment the fringes are displaced by a distance x when a glass plate of refractive index 1.5 is introduced in the path of one of the bemas.When this plate is replaced by another plate of the same thickness, the shift of fringes is (3)/(2) x.The refractive index of the second plate is : |
|
Answer» 2.25 shift of FRINGE due to path difference `lambda` is `beta = (D)/(d) lambda` Fringe shift in FIRST case is `X = (beta)/(lambda)(mu - 1) t` ...(i) Fringe shift in second case is `3/2x = (beta)/(lambda)(mu. - 1)t` `therefore (x)/(3/2x) = ((beta/lambda)(mu - 1) t)/(beta/lambda)(mu. -1)t = (mu - 1)/(mu. - 1)` then `mu . = 1.75` `because mu = 15` |
|
| 2674. |
lamda_pand lamda_(alpha) be the wavelengths of proton and alpha-particle of equal kinetic energy, then |
|
Answer» `lamda_p = (lamda_(alpha))/4` m = MASS of a particle K = kinetic energy of a particle For proton`lamda_p=h/(sqrt(2m_pK_p)) ""...(i)` For `alpha` - particle , `lamda _(alpha) = (h)/(sqrt(2m_(alpha)K_(alpha))` `lamda_(alpha) = h/(sqrt2(4m_p) K_p)"" ( :. K_p = K_(alpha)) ` `lamda_(alpha) = h / (2 sqrt(2m_p K_p))""...(ii)` DIVIDING (i) by (ii) , we get `lamda_p/lamda_(alpha)=(h/(sqrt(2m_pK_p)))/(h/(2sqrt(2m_pK_p)))` `lamda_p/lamda_(alpha)=2, " or " lamda_(p) = 2lamda_(alpha)` |
|
| 2675. |
Equipotential surfaces |
|
Answer» are closer in regions of large ELECTRIC fields COMPARED to regions of LOWER electric fields. |
|
| 2676. |
A resistance is connected to a capacitor in AC are the phase differece is (pi)/(4) between current and voltage. Whe the same resistance is connected to an inductor, phase difference becomes tan^(-1)(2). Power factor of the circuit when both capacitor and inductor are connect to the resistance will be |
|
Answer» 1 |
|
| 2677. |
A current of 0.5 A in the primary coil of a transfomer is reduced to zero at a uniform rate in 0.1 second. If the coefficient of mutual inductance is 3H, what is the emf induced in the secondary coil and charge in the magnetic flux per turn in the secondary coil if it has 50 turns? |
|
Answer» <P> Solution :DATA: `(dI_(P))/(DT) = -(0.5a)/(0.1 s) = -5A//s, M=3H, N_(s)= 50`(i) The emf induced in the secondary COIL `=-M(dI_(P))/(dt) = -3 xx (-5) = 15 V` (ii) `E_(S) = -N_(S)(dPhi_(S))/(dt)` `THEREFORE dPhi_(S) = -(E_(s)dt)/(N_(S)) = -(15 xx 0.1)/50 = -0.03` Wb This gives the change in the magnetic flux per turn in the secondary coil. |
|
| 2678. |
यदि द्विघात बहुपद p(x)=x^2+15x+44 के शून्यक alpha ,betaहो तो alpha^2+beta^2-alpha.beta का मान होगा - |
|
Answer» -357 |
|
| 2679. |
Whichof the following is themost suitable mateial for making permanent magnet ? |
|
Answer» Steel |
|
| 2680. |
A narrow beam of whit light goes through a slab having parallel faces. |
|
Answer» The light neve SPLITS in DIFFERENT colours. |
|
| 2681. |
A ball is shot from the ground into the air. At the height of 9.1 m, its velocity is v = (7.6 m//s)hati + (6.1 m//s)hatj, withhat ihorizontal and j upward. (a) To what maximum height does the ball rise? (b) What total horizontal distance does the ball travel? What are the (c) magnitude and (d) angle (below the horizontal) of the ball's velocity just before it hits the ground? |
|
Answer» Solution :We DESIGNATE the given velocity `v = (7.6 m//s)hati + (6.1 m//s)hatj` as `vecv_1`, as opposed to the velocity when it reaches the max height, `vecv_2` or the velocity when it returns to the ground `vecv_3`, and take y, as the launch velocity, `vecv_0`as usual. The origin is at its launch point on the ground. Different approaches are available , but since it will be be useful (for the rest of the problem ) to FIRST find the initial y velocity , that is how we will proceed . using eq. we have . `v__(1_y)^2 = (v_0y)^2 -2g DELTA y` substituting values , we have `(6.1 m//s)^2 = v_(0y)^2- 2 ( 9.8 m//s^2) (9.1 m)` Which yields `v_(0y) = 14.7 m//s` . Knowing that `v_(2y)` must equal 0 , we use eq. again but now with `Delta y = h` for the maximum height: `v_(2y)^2 = v_(0y)^2 - 2gh rArr 0 = (14.7 m//s)^2 - 2 (9.8 m//s^2) h` which yield h = 11 m (b) Recalling the derivation of eq. but using `v_(0y)` for `v_0 sin theta_0` and `v_(0x) cos theta_0` we have. `0 = v_(0y) t - 1/2 "gt"^2 , R = v_(0x) t` Which leads to` R = 2v_(0x) v_(0y)lg ` . noting that `v_(0x) = v_(1x) = 7.6 m//s`, we plug in values and obtain `R = 2 (7.6 m//s) (14.7 m//s) (9.8 m//s^2) = 23m` (c ) since `v_(3x) = v_(1x) = 7.6 m//s " and " v_(3Y) = -v_(0y) = -14.7 m//s` , we have `v_3 = sqrt(v_(3x)^2+ v_(3y)^2) = sqrt( (7.6 m//s)^2 + (-14.7 m//s)^2) = 17 m//s` (d) The angle (measured from horizontal for `vecv_3` is one of these possibilities : `tan^(-1) ((-14.7 m)/(7.6m)) = - 63^@ or117^@` |
|
| 2682. |
When a 15 V dc source was applied across a choke coil then a current of 5 Amp flows in it. If the same coil is connected to a 15 V, 50 rad/s ac source a current of 3 Amp flows in the circuit. Determine the inductance of the coil. Also find the power developed in the circuit and its resonance frequency if a 2500 muf capacitor is connected in series with the coil |
|
Answer» Solution :coil,`Z=sqrt(R^(2)+omega^(2)L^(2))` `I=(V)/(Z)=(V)/sqrt(R^(2)+omega^(2)L^(2))` For DE SOURCE, `omega = 0` `I=(V)/(R)impliesR=(15)/(5)=3Omegaldots|(i)` When ac is applied`I=(V)/(Z)` i.e.`Z=(15)/(3.0)=5Omega` `thereforeR^(2)+X_(L)^(2)=25` `X_(L)^(2)=25-9=16OmegaimpliesX_(L)=4Omega` `L=(4)/(40)=0.08Henry` Now when the CAPACITOR is connected is series`thereforeX_(C)=(1)/(omegaC)=(1)/(50xx2500xx10^(-6))=8Omega` `Z=sqrt(R^(2)+(X_(L)-X_(c))^(2))=sqrt(3+(48)^(2))=5Omega` `therefore`I=(15)/(5)=3A` `therefore ` `P_(av)=V_(RMS)I_(rms)COSPhi=I_(rmms)^(2)R=(3)^(2)xx3=27W` Resonance frequency f`f=(1)/(2pisqrt(LC))` `=(1)/(2pisqrt((0.08)xx2500xx10^(-6)))=(1000)/(2pixx5xx2sqrt2)` `(25sqrt2)/(pi)=11.25Hz` |
|
| 2683. |
Column A gives a list of possible set of parameters measured in some experiments . The variations of the parameters in the form of graphs are shown in column B. |
|
Answer» |
|
| 2684. |
Deduce the expression for the electrostatic energy stored in a capacitor of capacitance C and having charge Q. How will the The electric field inside the capacitor be affected when it is completely filled with a dielectric meterial of dielectric constant k? |
|
Answer» Solution :When the capacitor is filled COMPLETELY with a dielectric material of dielectric constant k, then capacitance BECOMES, C' = kC. Changed POTENTIAL difference, `V' = (Q)/(C')""[:. Q = " constant "]` `= (Q)/(kC)= (V)/(k)` Changed electric field, `E' = (V')/(d)= (V)/(kd)= (E)/(k)` The FINAL electric field will be `(1)/(k)` times of its previous value. |
|
| 2685. |
Electric force on alpha-particle placed in electric Field of 20 xx 10^4 N/C is ....... |
|
Answer» `3.2 XX 10^(-14)` N `=20 xx 10^(4) xx 2 xx 1.6 xx 10^(-19) = 6.4 xx 10^(-14)` N |
|
| 2686. |
Suppose that the particle in the above question is an electron projected with velocity v_x = 2.0 xx 10^(6) m s^(–1). If E between the plates separated by 0.5 cm is 9.1 xx 10^(2) N//C, where will be the electron strike the upper plate? (|e|=1.6 xx 10^(-19) C, m_e = 9.1 xx 10^(–31) kg). |
|
Answer» Solution :Velocity of the particle, `V_(X)=2.0xx10^(6)m//s` Separation of the TWO plates, d = 0.5 cm = 0.005 m Electric FIELD between the two plates, E = `9.1xx10^(2)N//C` Charge on an electron, q = `1.6xx10^(-19)C` Mass of an electron, `m_(e)=9.1xx10^(-31)` kg LET the electron STRIKE the upper plate at the end of plate L, when deflection is s. Therefore, `s=(qEL^(2))/(2mv_(x)^(2))` `L=sqrt((2dmv_(x)^(2))/(qE))` `=sqrt((2xx0.005xx9.1xx10^(-31)xx(2.0xx10^(6))^(2))/(1.6xx10^(-10)xx9.1xx10^(2)))` `=1.6xx10^(-2)` = 1.6 cm Therefore, the electron will strike the upper plate after travelling 1.6 cm. |
|
| 2687. |
A concave lens of glass, refractive index 1.5, has both surfaces of same radius of curvature R. On immersion in a medium of refractive index 1.75, it will behave as a, |
|
Answer» CONVERGENT LENS of FOCAL length 3.5 R f. = 3.5 R. |
|
| 2688. |
The width of a rectangular glass slab is 5 cm. From a point on its bottom surface, length rays are incident on its top face and after total reflection form a circle of light of radius 8 cm. What is the refractive index of the glass slab? |
|
Answer» Solution :Let O be a bright point at the bottom face of the rectangular slab. Light RAYS staring from O return to the bottom face after total reflection from the upper face of the slab. As a result, a circle of light of RADIUS OA = OB = 8cm is formed on the bottom face. So angle of incidence on the upper face is `theta_(c)` (critical angle) [Fig. 2.60]. According to the figure `OP = sqrt(OC^(2) + PC^(2)) = sqrt((4)^(2) + (5)^(2)) = sqrt(41) cm` `therefore " " "refractive index"` `mu= (1)/(sintheta_(c)) = (1)/((OC)/(OP)) = (OP)/(OC) = (sqrt41)/(4) = 1.6` 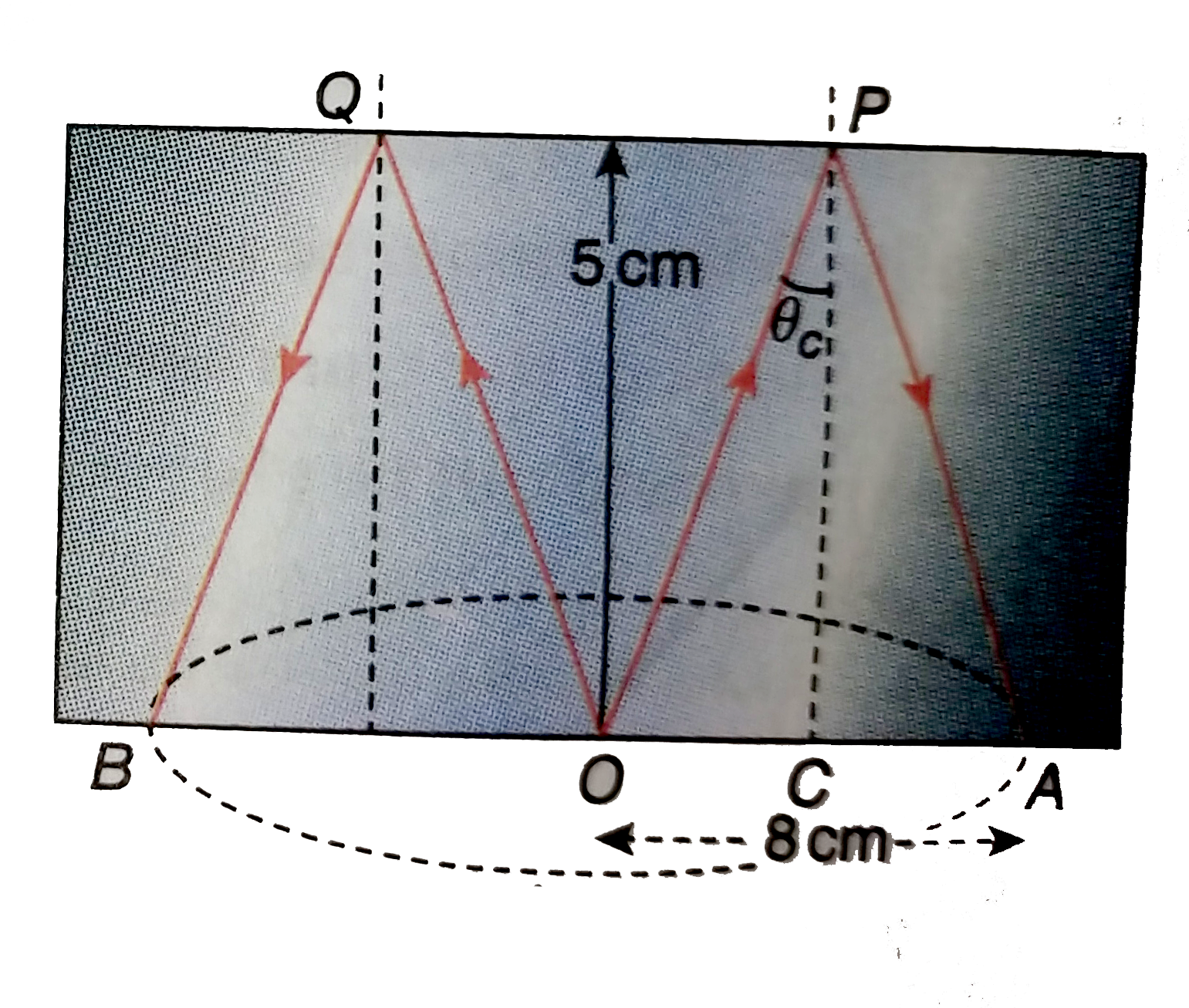
|
|
| 2689. |
An equilateral tringular loop ADC having some resistance is pulled with a constant velocity v out of a uniform magnetic field directed into the paper. At time t=0, side DC of the loop is at edge of the magnetic field. |
|
Answer»
`(AH)/(AE)=(GH)/(EC)` :. `GH=((AH)/(AE))EC` or `GH+((b-VT))/(b).a` `=a-((a)/(b)vt)` :. `FG=2GH=2[a-(a)/(b)vt]` Induced emf, `e=Bv(FG)=2Bv(a-(a)/(b)vt)` :. Induced current `i=(e)/(R )=(2Bv)/(R )[a-(a)/(b)vt]` or `i=k_(1)-k_(2)t` Thus `i-t` graph is a straight line with negative slope and positive intercept. 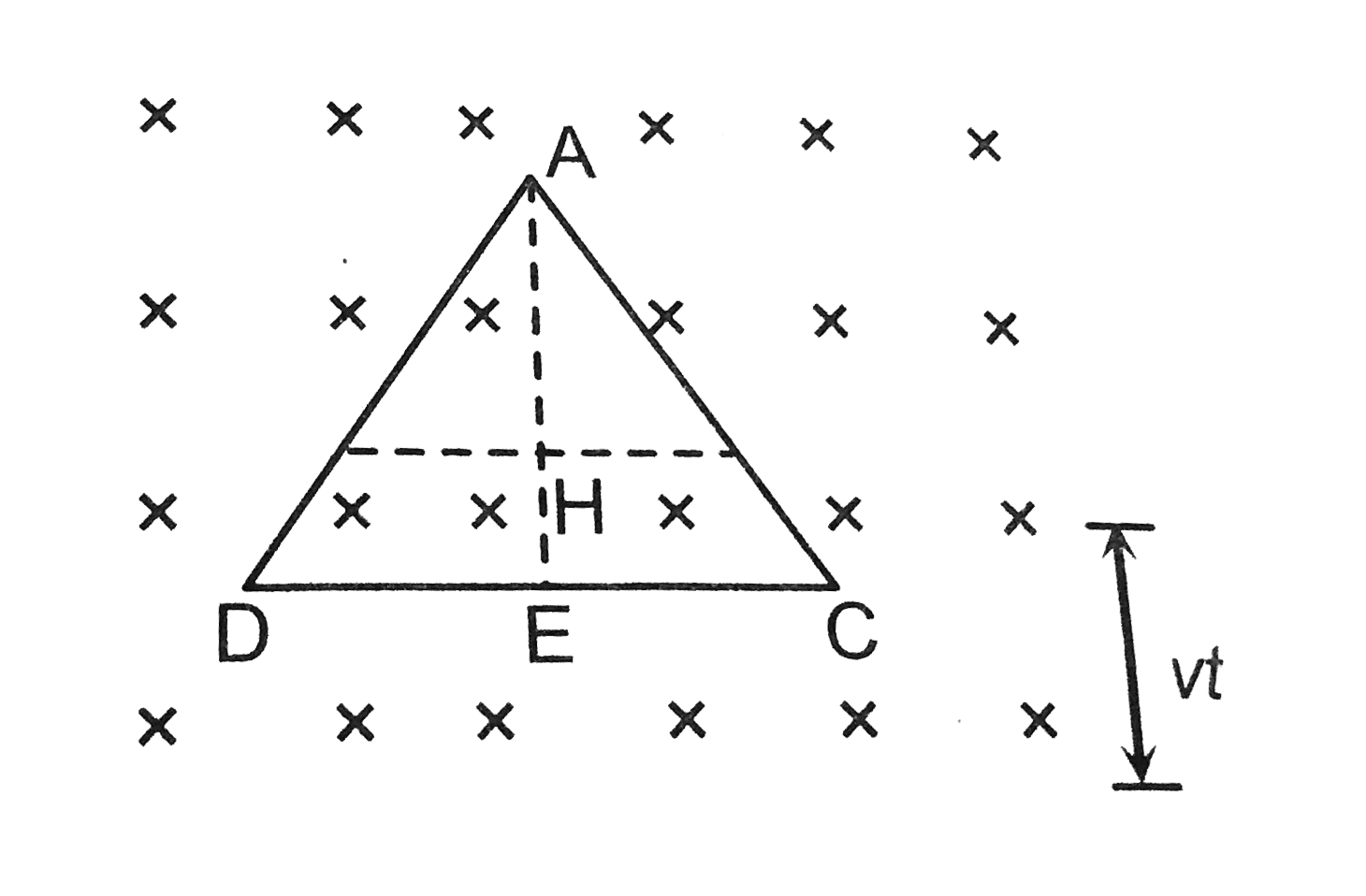
|
|
| 2690. |
The equation of an alternating voltage is V = 100 sin 100 pit volt. Its peak value and frequency are |
| Answer» Answer :A | |
| 2691. |
The R.I. of vaccum is_____and RI for air is_____ |
| Answer» SOLUTION :[1,1,003] | |
| 2692. |
Give Biot - Savart formula in vector form. |
|
Answer» `dvecB=mu_(0)/(4pi)(I(dveclxxvecr))/r^(2)` `bar(dB)=mu_(0)/(4pi)(VEC(Idl)xxvecr)/r^(3)` |
|
| 2693. |
A positive point charge q is placed at a distance 2 R from the surface of a metallic shell of radius R. the electric field at centre of shell due to indouced charge has magnitude |
|
Answer» zero |
|
| 2694. |
A set of n identical resistors,each of resistance R ohm when connected in series, have effective resistance X ohm and when connected in parallel the effective resistance is y Ohm. The relation between R,X and Y is given by |
|
Answer» `R=sqrt(XY)` When connected in series , `Y=R/n` So, `XY=nRtimesR/n=R^2` `thereforeR=sqrt(XY)` |
|
| 2695. |
The region inside a current carrying torodial winding is filled with tungsten of susceptibility 6.8 xx 10^(-5). What is the percentage increase in the magnetic field in the presence of the material with respect to the magnetic field without it ? |
|
Answer» Solution :The magnetic field in the current carrying torodial WINDING without TUNGSTEN is `B= muH` `THEREFORE (B- B_0)/( B_0) = (MU-mu_(0 ) )/( mu_(0) ) ""…(1)` But `mu= mu_(0)(1+ chi_(m) ) ` `therefore (mu)/( mu_0) = 1+ chi_(m) ` `therefore (mu)/( mu_0) -1 = chi_(m)` `therefore (mu- mu_0)/( mu_0) = chi_m` `therefore` Using this equation, `(B- B_0)/( B_0) = chi_m` `therefore` Percentage increase in the magnetic field in presence of tungsten is `(B- B_0)/( B_0) xx 100 = (6.8 xx 10^(-5) )xx 100` `= 6.8 xx 10^(-3)`% |
|
| 2696. |
Name the scientist who proved the missing link in differential equations of electromagnetic waves. |
|
Answer» Hertz |
|
| 2697. |
If critical frequency is 20 MHz for ionosphere, calculate the angle of transmission if 30 MHz frequency is transmitted. |
|
Answer» `cos ^(-1)((2)/(3))` |
|
| 2698. |
A light rigid wire of length 1 m is attached to a ball A of mass 500 g to one end. The other end of the wire is fixed, so that the wire can rotate freely in the vertical plane about its fixed and At the lowest point of the circular motion, the ball is given a horizontal velocity 6 m/s. Determined the radial component of the acceleration of the ball, when this rigid wire makes an angle 60^@ with the upward vertical (Takeg = 10 m//s^2) |
|
Answer» `10m//s^2` length of a rigid wire, l= 1 m mass of the ball, m = 500 g=0.5kg VELOCITY of ball at a point, C =v m/s  Motion of body in vertical plane is shown in the figure. In` DELTA BOC` ` cos 60^2 = (OB)/(OC)` `1/2 = h/1` ` RARR h = 1/2 m` ` therefore AB = OA + OB = l + h = 1+ 1/2 ` `AB= 3/2 m`....(i) According to the laws of CONSERVATION of energy, (KE+PE) at a point A= (KE + PE) at point C `1/2 "mu"^2 + 0 + 1/2 mv^2 + mg (AB)` `u^2 = v^2 + 2g . 3/2 ` ` 6^2 = v^2 + 2 xx 10 xx 3/2 ` ` v^2 = 6` ` therefore ` Radial component of acceleration of the ball ` a_C = (v^2)/(l) = 6/1 =6m//s^2` |
|
| 2699. |
Current coming from the battery and ammeter reading are |
|
Answer» `3/8A ,1/8 A` |
|
| 2700. |
An electron revolves round a nucleus of charge Ze. In order to excite the electron from the state n =2 to n =3, the energy required is 47.2 eV. Then Z is equal to : |
|
Answer» 3 |
|




 (
(