Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3351. |
At what angle should the axes of two polaroids be placed so as to reduce the intensity of the incident unpolarized light to (a) 1/4 (b) 1/2? |
| Answer» SOLUTION :`(a) 45^@, (B) 0^@ " or " 180^@` | |
| 3352. |
Imagine removing one electron form He^(4) and He^(3). Their energy levels, as worked out on the basis of bohr model will be very close. Explain why. |
| Answer» Solution :Imagine ONE electorn removed form `._2He^(4) and _2He^(3)`. As both the residual NUCLEI are very heavy compared to the mass of ELECTRON removed, therefore, their energy LEVELS, WORKED out on the basis of bohr model, will be very close. | |
| 3353. |
Choose the correct alternative: (a) Alloys of metals usually have (greater/less) resistivity than that of their consituent metals. (b) Alloys usually have much (lower/higher) temperature coefficients of resistance than pure metals. The resistivity of the alloy manganin is nearly independent of/increases rapidly with increase of temperature. The resistivity of a typical insulator (e.g., amber) is greater than that of a metal by a factor of the order (10^(22) // 10^(23)). |
|
Answer» Solution :(a) GREATER (b) Lower (C ) Nearly independent `10^(22)` |
|
| 3354. |
A cylindrical bar magnet is placed along the axis of a circular coil, will there bea current induced in the coin of the magnet is rotated about it's axis give reason. |
| Answer» SOLUTION :No, because the magnetic flux linked with the CIRCULAR coil does not CHANGE when the magnet is ROTATED about it.s axis. | |
| 3355. |
In L-C oscillatios of a circuit , which of the following is true at t=3T//4 (T=time period of the oscillation). Assume that at t=0, the capacitor is fully charged? |
|
Answer» Energy STORED in then inductor is ZER, while in CAPACITOR is MAXIMUM |
|
| 3356. |
A compound microscope consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective should an object be placed in order to obtain the final image at (a) the least distance of distinct vision (25 cm), and (b) at infinity? What is the magnifying power of the microscope in each case ? |
|
Answer» SOLUTION :`V_(e)=-25cm` `f_(e)=6.25cm.` Using lens formula, `(-1)/(25)-(1)/(u_(e))=(1)/(6.25) rArr (1)/(u_(e))=(-1)/(25)-(1)/(6.25)` `u_(e)=-5cm` Now `V_(0)=15-5=10cm` `f_(0)=2.0cm` `(1)/(upsilon_(0))=(-1)/(u_(0))=(1)/(f_(0))rArr (1)/(10)-(1)/(mu_(0))=(1)/(2)` `(1)/(u_(0))=(1)/(10)-(1)/(2)=(-5+1)/(10)=(-4)/(10)` `u_(0)=(-10)/(4)=-2.5cm.` Magnifying power `=(v_(0))/(1u_(0)1)(1+(D)/(f_(e)))` `=(10)/(2.5)xx(1+(25)/(6.25))` `=4(1+4)=20` B) `u_(0)=-6.25cm` `upsilon_(0)=15-6.25=8.75cm` `f_(0)=2.0cm` `(1)/(upsilon_(0))-(1)/(u_(0))=(1)/(f_(0)) rArr(-1)/(u_(0))=(1)/(f_(0))(-1)/(upsilon_(0))` `(1)/(mu_(0))=(1)/(2)-(1)/(8.75)=27//70` `u_(0)=-2.59cm` Magnifying power `M=(upsilon_(0))/(|u_(0)|)xx(D)/(f_(e))=(upsilon_(0))/(|u_(0)|)xx(25)/(6.25)` `M=(8.75xx27)/(8)xx(25)/(6.25)=13.51cm` |
|
| 3357. |
A body of mass 'm' is travelling with a velocity 'u' . When a constant retarding force 'F' is applied , it comes to rest after travelling a distance s_1 . If the initial velocity is 2u , with the same force F , the distance travelled before it comes to rest is s_(2) . then |
|
Answer» `s_2=2s_1` `:.S_2=4S_1` |
|
| 3358. |
The magnetic field within cylindrical region whose cross - section is indicated starts increasing at a constant rate alpha tesla/sec . The graph showing the variation of induced field with distance r from the axis of cylinder is : |
|
Answer»
|
|
| 3359. |
The separation between conduction bandof electromagnetic radiationrequired to generate an electronholepair in ti |
| Answer» SOLUTION :`1.74 XX 10^(-6) m` | |
| 3360. |
x-y plane separates two media. z gt= 0contains a medium of refractive index 1 and z lt= 0contains amedium of refractive index 2. A ray of light is incident from first medium along a vector hati + hatj + hatk ,the unit vector along refracted ray is |
|
Answer» `(1)/(2SQRT3) hati + (1)/(2sqrt3) hatj - sqrt(5/6) hatk` |
|
| 3361. |
A cube of side b has a charge q at each of its vertices. The electric field due to this charge distribution at the centre of the cube is |
|
Answer» `(Q)/(b^(2))` |
|
| 3362. |
In the laboratory method for measuring the latent heat of stream, the steam is passed through the device shown below. The function of the device is |
|
Answer» to PREVENT CONDENSED steam from reaching the calorimenter |
|
| 3363. |
The sum of the heights of transmitting and receiving attennas in line of sight of communication is fixed at h, find the height of two antennas when r ange is maximum. |
|
Answer» `h//2` `v=sqrt(2Rh_(T))+sqrt(2Rh_(R))` Given `h_(T)+h_(R)=h` and LET `h_(T)=H`, then `h_(R)=h-H` `therefore r=sqrt(2R)[sqrt(H)+sqrt(h-H)]` For r to be MAXIMUM, `(dr)/(dH)=sqrt(2R)[(1)/(2sqrt(H))+(1)/(2sqrt(h-H)(-1))]=0` or `(1)/(2sqrt(H))-(1)/(2sqrt(h-H))=0` or `H=h-H` or `H=(h)/(2)` |
|
| 3364. |
Which of th efollowing statements are correct? |
|
Answer» A ray of light is incident on a plane MIRROR and gets reflected. If the mirror is rotated through an angle `theta`, then the reflected ray gets deviated through angle `2theta` `=2i-(2i-2theta)=2theta`  Total deviation `DELTA=delta_(1)+delta_(2)` `=(180^(@)-2theta)+180^(@)-2(alpha-omega)` `=360^(@)-2ALPHA` 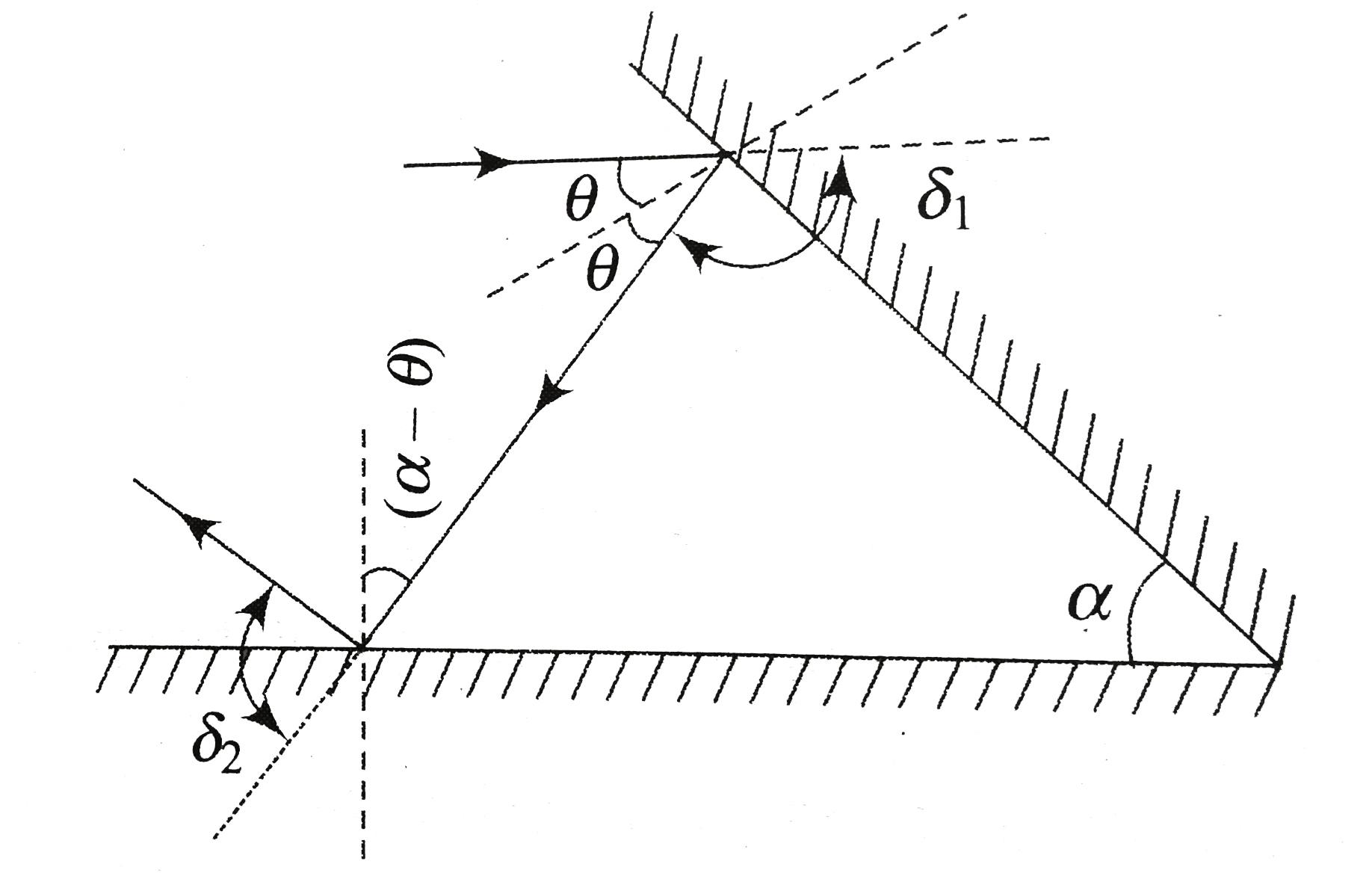 which is independent of angleof incidence. c. Power of a plane mirror is zero. d. Velocity of the image toward the object `=v+v=2v.` |
|
| 3365. |
The four Maxwell's equations and the Lorentz force law (which together constitution the fundations of all the classical electromagnetism) are listed below: (i) oint vecB.vec(ds)=q//(in_0) (ii) oint vecB.vec(ds)=0 (iii) oint vecE.vec(dl)=-d/(dt) int_svecB.vec(ds) (iv) oint vecB.vec(dl)=mu_0I+mu_0d/(dt)int_s vecb.vec(ds) Lorentz force law: vecF=q(vecE+vecvxxvecB) Answer the following question regarding these equation: (a) Give the name (s) associated with some of the four equation above. (b) Which equations above contain source vecE and vecB and which do not? what do the equations reduce to in a source-free region? (c) Write down Maxwell's equations for steady (i.e. time independent) electric and magnetic fields. (d) If magnetic monopoles existed, which of the equations would be modified? Suggest how they might be modified? (e) Which of the four equations shown that magnetic field lines cannot start from a point nor end at a point? (f) Which of the four equations show that electrostatic field lines cannot form closed loops? (g) The equations listed above refer to integrals of vecE and vecBover loops/surfaces Can we write down equations for vecE and vecB for each point in space? (h) Are the equations listed above true for different types of media: dielectrics, conductors, plasmas etc.? (i) Are the equation true fora arbitrarily high and low values of vecE,vecB,q,I? |
|
Answer» Solution :(a) (i) Guss's law in electrostatics. (ii) Guss's law in magnetostatics. (iii) Faraday's law of electromagnetic induction (iv) Ampere's Circutal law with Maxwell's modification. (b) Equations (i) and (iv) contain the source Q, I: equations (ii) and (iii)do not. To obtain equations in source free region, simply put `q=0` and `I=0`. Then `oint vecE.vec(ds)=0`[from eqn(i)] and `oint vecE.vec(dl)=mu_0in_0d/(dt)int_svecE.vec(ds)` [From eq(iv)] (c) Maxwell's equations will be TIME independent if the derivative of the physical quantity involved with time is zero. Putting this concept on the right hand side of EQUATION (iii) and (iv), we have Maxwell's equations as: `oint vecE.vec(ds)=Q/(in_0)oint vecE.vec(ds)=0` `oint vecE.vec(dl)=0oint vecE.vec(dl)=mu_0I` (d) Equation (ii) and (iii) would be modified . Equation (ii) is based on the fact that monopoles do not exist. If the monopoles exist, the right hand side would contain a term say `q_m` representing magntic dipole strength, analogous to Gauss's law, in electrostatics, we would have `oint vecE.vec(ds)=q_mxxcostant.` Further equation (iii) would also be modified. An additional term `I_m` representing the current due to flow of magnetic charge would have to be included on the right hand side of equation (iii) analogous to the electric charge current of equation (iv), we would have `oint vecE.vec(dl)=I_mxxconstant-d/(dt)int_svecB.vec(ds)` All this is of COURSE, based on the expection of symmetry of from of the equaitons for E and B. Nature may never show up monopoles or else even if monopoles exist, the actual modification of Maxwell's equations might be very different. (e) Equation (ii) only (f) Equation (i) shows that the elctrostatic field lines cannot from closed loops, as electrostatic field field lines cannot pass through conductors. (g) Yes, we can. Maxwell's equations can be cast as different equations valid at every POINT in space and at every instant. (h) Maxwell's equations are true in all media. But in macroscopic media, it is usually convenient to write down equations for average of `vecE and vecB` over regions which are small macroscopically but large enough to contain a very large number of atoms etc. The resulting macroscopic Maxwell's equtions are of great practical use. (i) Maxwell's equations are the basic laws of classical electromagnetism. They are true in all media and for any value of E,B,q,I ect. whithin the domain of validity of classical electromagnetism. The precise domain of validity is hard to specify and need not concern us here. |
|
| 3366. |
A : In Young.s interference experiment the incident light used is white. When one slit is convered with red filter and the other with blue filter, the phase difference at any point on the screen will continuously change and producing uniform illumination. R : Two independent sources of light would no longer act as coherent sources. |
|
Answer» Both A and R are true and R is the CORRECT EXPLANATION of A |
|
| 3367. |
To form a jeep, two squares of side length 10cm & 20cm and two circles of perimeter 15cm each are connected as shown. The centre of bigger square is at origin and x-y axes are as shown. The x coordinate of centre of mass of this model is :- |
|
Answer» `X=-5cm` `x=(80xx0+40xx(-15)+15xx(-15)+15xx5)/(80+40+15+15)` `=-5cm` |
|
| 3368. |
In the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by r=(mv)/(qB)...(1) Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency f_(osc) of the electrical oscilliator, or f=f_(osc)("resonance condition")...(2) This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency f_(osc) that is equal to the natural frequency f at which the proton circulates in the magnetic field. Combining equation 1 and 2 allows us to write the resonance condition as qB=2pimf_(osc)..(3) For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency f_(osc)We then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam. Ratio of radius of successive semi circular path |
|
Answer» `sqrt1:sqrt2:sqrt3:sqrt4..` for second time `KE_(2)=3/2qV` for third time `KE_(3)=5/2qV` hence the ratio of RADII are `r_(1):r_(2):r_(3):....::sqrt(2mqv)/(qB):sqrt(2m3qv)/(qB):...` `r_(1):r_(2):r_(3):....::sqrt1:sqrt3:sqrt5 ...` |
|
| 3369. |
In the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by r=(mv)/(qB)...(1) Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency f_(osc) of the electrical oscilliator, or f=f_(osc)("resonance condition")...(2) This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency f_(osc) that is equal to the natural frequency f at which the proton circulates in the magnetic field. Combining equation 1 and 2 allows us to write the resonance condition as qB=2pimf_(osc)..(3) For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency f_(osc)We then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam. Change in kinetic energy of charge particle after every time period is: |
| Answer» Solution :N//A | |
| 3370. |
In the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by r=(mv)/(qB)...(1) Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency f_(osc) of the electrical oscilliator, or f=f_(osc)("resonance condition")...(2) This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency f_(osc) that is equal to the natural frequency f at which the proton circulates in the magnetic field. Combining equation 1 and 2 allows us to write the resonance condition as qB=2pimf_(osc)..(3) For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency f_(osc)We then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam. If q//m for a charge particle is 10^(6),frequency of applied AC is 10^(6)Hz.Then applied magnetic field is |
|
Answer» `2pi` tesla |
|
| 3371. |
In the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by r=(mv)/(qB)...(1) Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency f_(osc) of the electrical oscilliator, or f=f_(osc)("resonance condition")...(2) This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency f_(osc) that is equal to the natural frequency f at which the proton circulates in the magnetic field. Combining equation 1 and 2 allows us to write the resonance condition as qB=2pimf_(osc)..(3) For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency f_(osc)We then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam. Distance travelled in each time period are in the ratio of: |
|
Answer» `sqrt1+SQRT3:sqrt5+sqrt7:sqrt9+sqrt11` |
|
| 3372. |
In the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by r=(mv)/(qB)...(1) Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency f_(osc) of the electrical oscilliator, or f=f_(osc)("resonance condition")...(2) This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency f_(osc) that is equal to the natural frequency f at which the proton circulates in the magnetic field. Combining equation 1 and 2 allows us to write the resonance condition as qB=2pimf_(osc)..(3) For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency f_(osc)We then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam. For a given charge particle a cyclotron can be "tune" by: |
|
Answer» changing applied `A.C.` voltange only |
|
| 3373. |
A person cannot see beyond a distance of 50 cm.The power of corrective lens required to see distant object is |
|
Answer» −1.5 D |
|
| 3374. |
a. What type of biasting is used here ? b. What happens to the depletion region ? c. Will the diode conduct or not ? |
| Answer» SOLUTION :a . REVERSE biasingb. BECOMES thickerc. No | |
| 3375. |
An unknown frequency x produces 8 beats per second with a frequency of 250 Hz 12 betas with 270 Hz source, then x is : |
|
Answer» 258 hz also v= 270 `pm 12 "" rArr v = 258 or 282 `Hz. hence v = 258 Hz. CORRECT choice is (a) . |
|
| 3376. |
A convex lens of focal length f is placed some - where in between the object and a screen. The distance between object and screen is x. If magnification produced is m, the focal length of the lens is : |
|
Answer» `(mx)/((m+1)^(2))` `f = (uv)/(u+f)` `f=(uv[(v+u)/(u^(2))])/((v+u)[(v+u)/(u^(2))])=((v+u)(v)/(u))/(((v+u)/(u)))` `therefore "" f=((v+u)(v)/(u))/(((v)/(u)+1))` `therefore v + u = x and (v)/(u) = m` `therefore f = (x.m)/((m+1)^(2)).` |
|
| 3377. |
A rod resistor obeys non-linear relationship between V and l-according to I = sqrtV//10 This rod is connected in series with a resistance to a 20 V battery of practically no resistance. Find this series.resistance for the following cases(a) the current in the circuit is 0.4 A. (b) the power dissipated in the rod is twice that dissipated in the resistance |
|
Answer» SOLUTION :`10OMEGA` 10sqrt((10)/(3))OMEGA` |
|
| 3378. |
From Bohr's theory obtain the de Broglie wavelength of an electron orbiting around the nucleus. |
|
Answer» Solution :From Bohr.s QUANTISATION angular momentum `mvr=nh//2pi ,2pir=nh//mv 2pi r=n LAMBDA` `THEREFORE lambda=2 pir//n` |
|
| 3379. |
A fuse F_(1) is connected across a source of variable voltage and the voltage is increased gradually. The fuse blows out just when the reading of the voltmeter and ammeter reaches 1.0 V and 1.0 A respectively (see figure (i)). The experiment is repeated with another fuse F_(2) and the reading of the voltmeter and ammeter when it blows out is 2.4V and 1.2 A respectively. (a) The two fuses are connected in parallel as shown in figure (ii). Voltage is increased gradually. find the reading of the ammeter when any one of the fuses blows out. (b) The two fuses are connected in series as shown in figure (iii). find the reading of the voltmeter at the point one of the fuses blows out. |
|
Answer» (B) 3.0 V |
|
| 3380. |
a. What type of biasting is used here ? b. What happens to the depletion region ? c. Will the diode conduct or not ? |
| Answer» SOLUTION :a. FORWARD biasingb. BECOMES thinnerc. YES | |
| 3381. |
The magnetic intensity H at a point lying on the axial line of a bar magnet of magnetic moment M and effective length '2l' is approx : |
|
Answer» `M/d^2` |
|
| 3382. |
A screen is at a distance of 2m from narrow slits that are illuminated with light of 589 nm. The 10th minimum lies at 0.005mon either side of the central maximum, then the distance between the slits will be |
|
Answer» `0.024 MM` |
|
| 3383. |
Photographs of the ground are taken from an aircraft at an altitude of 2000 m by a camera with a lens of focal length 0.50m. The size of the film in the camera is 0.18m xx 0.18m. What area of the ground can be photographed by this camera in a single shot? |
|
Answer» Solution :`-U=2000m "" F=0.50m` Size of the image`0.18m xx 0.18m` Using the formula, `(1)/(f)=(1)/(V)-(1)/(u)` We get,`(1)/(0.50)=(1)/(v)+(1)/(2000), v=0.50m` `THEREFORE` Image will be formed at the focus. `m=(v)/(u)=(0.5)/(2000)=0.00025` `therefore ` Size of the object on the ground will COVER an area of`(0.18)/(0.00025)xx(0.18m)/(0.00025)` i.e., Area on the ground`=720m xx 720m`. |
|
| 3384. |
Referring to the previous illustration (a) What is the significance of positive and negative values of instantaneous velocities?(b) What are the distance covered and displacement during t= 2 sec? |
|
Answer» Solution :(b) x=t(t-1)`rArr` v=2t-1`rArr`v=0at `t=1//2sec` Displacement =`OVERSET(2)underset(0)intvdt`=`overset(2)underset(0)int(2t-1)dt=(t^(2)-t)` `overset(2)underset(0)int=4-2=2m` Displacement=`overset(V2)underset(0)int|v|dt+overset(2)underset(v2)int|v|dt=(t^(2)-t)|_(0)^(v2)+|(t^(2)-t)|_(0)^(v2)+|=|(1)/(4)-(1)/(2)|+|4-2-(1)/(4)+(1)/(2)|rArr(1)/(4)+2(1)/(4)=2.5m` |
|
| 3385. |
Two long straight parallel wires A and B separated by a distance d, carry equal current I flowing in same direction as shown in the figure. (a) Find the magnetic field at a point P situated between them at a distance x from one wire. (b) Show graphically the variation of the magnetic field with distance x for 0 lt x lt d. |
|
Answer» Solution :(a) Magnetic field at POINT due to current I in wire A, `B_A= (mu_(0) I)/(2pi x) uparrow` and magnetic field due to current I in wire B, `B_(B)=(mu_(0) I)/(2pi (d-x)) downarrow` Net magnetic field `B=(B_(A)-B_(B)) uparrow =(mu_(0)I)/(2pi) [1/x-(1)/((d-x))] ` `rArr B=(mu_(0)I)/(2pi) (d-2pi)/(x(d-x)) uparrow`  (b) Variation of magnetic field B with DISTANCE x is shown here. For `x=d/2` magnetic field B=0. For `x lt d/2` magnetic field B is directed UPWARD and for `x gt d/2` magnetic field B is directed downward. |
|
| 3386. |
How is a galvanometer converted into a voltmeter? |
Answer» Solution :A galvanometer can be converted into a voltmeter by CONNECTING a high resistance in series with it.  In figure, p.d. across AB is `V=(R+G)I_g` `R=V/I_g-G` To convert a galvanometer into a voltmeter , a high resistance is connected in series with the coil. The galvanometer with this modification is called a voltmeter. The value of the high resistance R to be connected in series with the coil depends on the maximum potential difference to be measured . If `I_g` be the current for a FULL SCALE DEFLECTION then, `V=I_g(G+R)` G is the resistance of the galvanometer.  `therefore R=V/I_g-G` Since G and R are constants , the scale can be graduated to read potential differences directly. A voltmeter is used for measurement of potential difference . It should be connected in parallel in a circuit. |
|
| 3387. |
An image I is formed of point object O by a lens whose optic axis is AB as shown in figure. (a) State whether it is a convex lens or concave? (b) Draw a ray diagram to locate the lens and its focus. |
|
Answer» SOLUTION : (i) Concave lens always forms an erect IMAGE. The given image I is on the other SIDE of the optic axis. Hence, the lens is convex. (ii) Join O with I. LINE OI cuts the optic axis AB at optical centre (P) of the lens. The dotted line shows the position of lens.  From point O, DRAW a line parallel to AB. Let it cut the dotted line at M. Join M with I. Line MI cuts the optic axis at focus (F) of the lens. |
|
| 3388. |
Explain the superposition principle for static electric forces and write its general equation. |
|
Answer» Solution :To find force acting on a charge by other charges, principle of superposition is also used with Coulomb.s law. "When more than one Coulombian forces are acting on a charge, the resultant coulombian force acting on it is equal to the vector sum of the individual forces."  Suppose `q_(1), q_(2)` and `q_3` are charges of a system as shown in figure. Let `r_(1), r_(2)`and `r_3` are their respective position vectors from ORIGIN .O.. If `vecF_(12)` is force acting on `q_(1)`by `q_(2)`, then `vecF_(12) = 1/(4piepsilon_(0)).(q_(1)q_(2))/r_(12)^(2).hatr_(12)`..........(1) And `vecF_(13)` is force acting on `q_(1)` by `q_(3)`, then `vecF_(13) = 1/(4pi epsilon_(0)).(q_(1).q_(2))/r_(13)^(2).vecr_(13)`.........(2) Where `vecr_(12)` is vecor in direction along `q_(2)` to `q_(2)`. `therefore vecr_(12) = vecr_(2)-vecr_(1)` and `vecr_(13)` is vector in direction along `q_(3)` to `q_(1)`. `therefore vecr_(13) = vecr_(3) - vecr_(1)` If `VECF` is force on `q_(1)` by `q_(2)` and `q_(3)`, then `vecF = vecF_(12) + vecF_(13)` `=1/(4pi epsilon_(0)).(q_(1)q_(2))/r_(12)^(2) + 1/(4pi epsilon_(0)).(q_(1).q_(3))/r_(13)^(2).hatr_(13)` Resultant force on a charge due to more thai three charges is shown in figure (b).  In general, if in system of `q_(1), q_(2), q_(3)`,........... `q_(n)`, force acting on `q_(1)` by other charges. `vecF_(1) = vecF_(12) + vecF_(13) + vecF_(14) +`............ `vecF_(n)` `=1/(4piepsilon_(0)) [ (q_(1).q_(2))/vecr_(12) + (q_(1)q_(3))/r_(13)^(2).r_(13) +....(q_(1)q_(2))/r_(1N)^(2).hatr_(1n)]` `=q_(1)/(4pui epsilon_(0)) sum_(i=2)^(n_(1)).q_(1)/r_(1I)^(2).r_(1i)` {where i=1,2,3,.......n) The vector sum is obtained as usual by the parallelogram law of addition of vectors. All of electrostatics is basically a consequence of Coulomb.s law and superposition principle. |
|
| 3389. |
The electromagnetic waves have wavelength range ? |
| Answer» SOLUTION :It RANGES from `6xx10^-13m` to more than `10^+44m`. | |
| 3390. |
A Ge specimen is doped with Al. The concentration of acceptor atoms is 10^21 atoms//m^3. The intrinsic concentration of electron hole pairs is ~10^19//m^3. What is the concentration of electrons in the specimen ? |
|
Answer» `10^17//m^3` |
|
| 3391. |
The speaker of a public address system emits 20 kW power, considering it a point source. What is the sound intensity level at a point 4.00 m away ? |
| Answer» ANSWER :B | |
| 3392. |
A planet is revolving round the sun in elliptical orbit. Its closest distance is r and farthest distance is R. If the orbital velocity closestto the sun is v, then velocity v at farthest point is : |
|
Answer» `(vr)/(R )` `therefore I_(1)omega_(1)=I_(2)omega_(2) or MR_(1)^(2)omega_(1)=MR_(2)^(2)omega_(2)` Now `omega_(1)=(v)/(r ) and omega_(2)=(V)/(R )` `therefore r^(2)xx (v)/(r )=R^(2)xx(V)/(R ) or vr=V.R` or `V=(vr)/(R )`. CORRECT choice is (a). |
|
| 3394. |
What is the nature of final image in a compound microscope? |
| Answer» SOLUTION :It is VIRTUAL and INVERTED. | |
| 3395. |
If the escape velocity of the body which is thrown from earths surface is V_e, then the escape velocity of the body if it is thrown at an angle theta from horizontal earths surface is |
|
Answer» `V_e` |
|
| 3396. |
In the figure shown, at what distance (a) E_2 will appear to E_1 (b) E_1 will appear to E_2 |
|
Answer» (B) `h_(app)=10+(1.5)(10)=25 cm` |
|
| 3397. |
What is the modulation index of AM, if the voltage amplitude of the carrier wave is 2kV and side band voltage amplitude is 200V. |
| Answer» SOLUTION :`A_s=(muA_c^<)/2, MU= (2A_s)/A_c =(2*2000)/2000=0.2` | |
| 3398. |
Two bodies A ( of mass 1 kg ) and B (of mass 3 kg ) are dropped from heights of 16m and 25m respectively. The ratio of time taken by them to reach the ground is |
|
Answer» `4/5` |
|
| 3399. |
When electrons drift in a metal from lower to higher potential, does it mean that all the 'free' electrons of the metal are moving in the same direction ? |
| Answer» Solution :All the free ELECTRONS are not MOVING in the same direction. In fact, the drift VELOCITY is SUPERPOSED over the large random velocities of electrons. | |
| 3400. |
A ray of light travelling in water is incident on a glass plate immersed in it. When the angle of incident is 51^(@) the reflected ray is totally plane polarized. Find the refractive index of glass. Refractive index of water is 1.33. |
|
Answer» SOLUTION :Angle of incidence `=theta_(p)=51^(@)` 51° Since at this incidence angle, reflected ray is totally plane POLARIZED, using Brewster.s law, refractive index of GLASS W.r.t. water is, `n.=tantheta_(p)=tan51^(@)=1.235` But `n.=("refractive index of glass "(n_(g)))/("refractive index of water "(n_(g)))` `:.n_(g)=n.n_(w)=1.235xx1.33=1.64` |
|



