Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3301. |
Given that the angle of minimum deviation for a colour is 43^(@)48' and its RI = 1.588, Calculate refracting angle of the prism. |
|
Answer» SOLUTION :`D=43^(@)48., n=1.588` `n=(SIN((A+D)//2))/(sinA//2)` `=(sin(A//2+(43^(@)48.)//2))/(sinA//2)` `=(sin(A//2 +21^(@)54.))/(sinA//2)` `1.588=(siniA//2cos21^(@)54.+sin21^(@)54.cosA//2)/(sinA//2)` `1.588=cos21^(@)54.+sin21^(@)54.+sin21^(@)54. (1)/(tanA//2)` `=0.9278+0.3730+(1)/(tanA//2)` `0.6602=0.3730xx(1)/(tanA//2)` `tanA//2=0.5649` `A//2=29^(@)28.` `therefore A=58^(@)56.` |
|
| 3302. |
Radiation of wavelength 180 nm eject photoelectrons from a plate whose work function is 2.0 eV. If a uniform magnetic field of flux density5.0xx10^(-5)T is applied parallel to plate, what should be the radius of the path followed by electrons ejected normally from the plate with maximum energy: |
|
Answer» 0.074 m Here `lambda= nm=180xx10^(-19)m` `w=2*0eV=2*0xx1*6xx10^(-9)J` `:.E=7*8xx10^(-19)J` Also `(1)/(2) mv^(2)=E:. V= sqrt((2E)/(m))` So `v=sqrt((2xx7*8xx10^(-19))/(9*1xx10^(-31)))=1*31xx10^(6)m//s` Radius r in a magnetic field of induction B is given by `BEV=(mv^(2))/(r) or r=(mv)/(eB)` Using `B=5xx10^(-5)T` Then `r=0*149m` |
|
| 3303. |
water flow alonga horizontal pipe of variable cross section. At a point where the velocity of flow is 0.3 m/s , the pressure is 1400N/m^2 . What is the pressure at the point where the velocity of flow is 0.6 m/s ? |
|
Answer» Solution :A =` 0.01m^2 x = 0.2cm = 0.002 m v = 0.03 ms^-1`Horizontal force to move the plate `F = (etaAv)/(x) = (1.55 XX .01 xx 0.03)/(.002)` = 0.2325 N. |
|
| 3304. |
Repeal above exercise for a proton which is made of two up and one down quark. |
Answer» Solution :For proton two up and ONE down quark 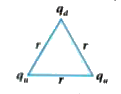 `q_(d)= -(1)/(3)e` `q_(u) = +(2)/(3) e` `r=10^(-15)` m `:.` Potential energy of system `U =k[(q_(u)q_(u))/(r)+(q_(u)q_(d))/(r)+(q_(u)d_(d))/(r)]` `=k[((2)/(3)exx(2)/(3)e)/(r)+((2)/(3)exx(-(1)/(3)e))/(r)+((2)/(3)exx(-(1)/(3)e))/(r)]` `=(k)/(r)[(4)/(9)e^(2)-(2)/(9)e^(2)-(2)/(9)e^(2)]` `=(ke^(2))/(9R)[4-2-2]` `=(ke^(2))/(9r)[0]` =0 `:.` Ratio of potential energy of proton to iti mass is zero |
|
| 3305. |
Two independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L_(2) by a plane passing through a diameter. L_(1) is kept above the axis and L_(2) below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S_(2) , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L_(2) is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L_(2) . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416. QDistance between the images Si and S_(2) will be |
|
Answer» 1 mm |
|
| 3306. |
The coil of dynamo is rotating in a magnetic field. The devloped induced e.m.f. changes and the number of magnetic lines of force also changes. Which of the following conditions is correct? |
|
Answer» Linesof force mnimum but induced e.m.f.Is ZERO |
|
| 3307. |
Two independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L_(2) by a plane passing through a diameter. L_(1) is kept above the axis and L_(2) below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S_(2) , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L_(2) is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L_(2) . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416. Q0.25 mm |
|
Answer» 7200 Å |
|
| 3308. |
A beam of light is partially reflected and partially refracted from a surface. The angle between the reflected and refracted light is 90^@. The angle of refraction is 30^@. The angle if incidence must be : |
| Answer» Answer :B | |
| 3309. |
Two independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L_(2) by a plane passing through a diameter. L_(1) is kept above the axis and L_(2) below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S_(2) , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L_(2) is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L_(2) . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416. Q Phase difference between the light waves 0.1 mm from along the screen, where intensity is half the maximum value, is |
|
Answer» ) tt/2 |
|
| 3310. |
Maxwell’s equation laws of |
|
Answer» ELECTRICITY only |
|
| 3311. |
If g_(E ) and 8_(M) are the accelerations due to gravity on the surfaces of the earth and the moon respectively and if Millikan oil drop experiment could be performed on the two surfaces, one will find the ratio("electronic charge on moon")/("electroniccharge on earth") to be: |
|
Answer» 0 `THEREFORE ("Electronic charge on moon")/("Electronic charge on earth")=1` So correct choice is (d). |
|
| 3312. |
What happened when the grandmother didn't pray for the first time? |
|
Answer» She fell ILL the next day |
|
| 3313. |
When your friend chewsa wintergreen life saver in a darkroom, you see a faint flash of blue light from his mouth. How? |
| Answer» Solution :This DISPLAY of light is OFTEN calledsparking. It occurs dueto ELECTRIC discharge of the electrostatic changes produced in CHEWING the wintergreenlife saver. | |
| 3314. |
State Biot- Savart law. Use to obtain the magnetic field at a point due to a long, staright current carrying wire. |
|
Answer» Solution :For statement of Biot - Savart law, refer to point Number 6 under the heading "Chapter At A Glance". LET CD be a long, staright current carrying wire and P be a point situated at a normal distance R from the wire. Consider a current element `I vecdl` situated at a distance OA = I. If AP = r, then due to `DB = (mu_0)/(4pi) (I dl sin theta)/(r^2)` As PER figure `sin theta = sin (90^@ - phi) = cos theta` `:. I = R tan phi` `:. dl = R SEC^2 phi CDOT d phi` and `r = R sec phi` `:. dB = (mu_0)/(4pi)cdot ((R sec^2 phi_2.d phi)cos phi)/((R sec phi^2)) = (mu_0)/(4pi) cdot (I cos phi cdot d phi)/(R)` Therefore, the magnetic field due to whole wire CD will be `B = (mu_0 I)/(4 pi R) int_(-phi_1)^(phi_2) cos phi . d phi = (mu_0 I)/(4 pi R) [sin phi_2 - sin (-phi_1)] = (mu_0 I)/(4 pi R) [ sin phi_2 + sin phi_2]` Here `phi_2` has been taken +ve but `phi_1` has been taken -ve because it is in a direction opposite to that of `phi_2` For a long long wire (or infinitely long wire) `phi_1 = phi_2 = 90^@`, therefore `B = (mu_0 I)/(2 pi R)` 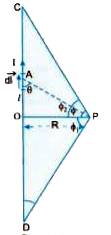
|
|
| 3315. |
Two bodies of mass 2 kg and 5 kg have position (1 m, 2 m, 1 m) and (3 m, 2 m, -1 m) respectively. The position vector of centre of mass is |
|
Answer» `(frac{17}{7}HATI + 2hatj - frac{3}{7}hatk)m` |
|
| 3316. |
One mole of an ideal gas at an initial temperature of TK does 6 R joule of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of the gas will be: |
|
Answer» `(T+4)K` `6R =(R )/((5)/(3)-1)(T-T_(2))` `T_(2)=(T-4)K`. `THEREFORE` Correct choice is (c ). |
|
| 3317. |
Two identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is: |
|
Answer» v From `vecv_(cm) = (m_1vecV_1 + m_2vecV_2)/(m_1 + m_2) , ""vecV_(cm) = (m xx 2V - mv)/(m + m) = v/2` [The direction of motion of the first particle is taken as positive.]So the velocity of the centre of mass of the system is v/2 in the direction of motion of the particle having LARGER SPEED. 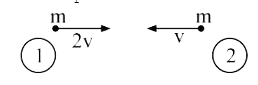
|
|
| 3318. |
A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north up pointing down at 22^@ with the horizontal. The horizontal component of the earth's magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth's magnetic field at the place. |
Answer» Solution : Horizontal COMPONENT of Earth.s magnetic field, `B_(h) B COS PHI` `therefore B= (B_(h) ) /( cos phi) ` `therefore B= (0.35)/( cos 22^(@) )` `therefore B= (0.35) /( 0.9272) ` `therefore B= 0.3775` G (Gauss) |
|
| 3319. |
Photoelectrons from metal do not come out with same energy . Most appropriate explanation is |
|
Answer» Someelectrons of a metal is average energy required to pull out electrons |
|
| 3320. |
A constant force actson a body of mass m, at rest and produces a velocity 'v' over a displacement 's_1'. The same force acts on another body of mass m_2 at rest and produces the same velocity. 'v' over a displacement 's_2'. The ratio of the displacements is |
|
Answer» `m_1 : m_2` |
|
| 3321. |
Mention the function of any two of the following used in communication system : (i) Transducer (ii) Repeater (iii) Transmitter (iv) Bandpass Filter [Any two] |
|
Answer» Solution :(i) Transducer : A transducer is a device which converts one form of energy into another. In electronic communication SYSTEMS, an electrical transducer is used. (ii) Repeater : When the distance of destination from the TRANSMITTER is very large or when the TRANSMITTED SIGNAL is OBSTRUCTED by mountains, etc., repeaters are installed along the path of the signal. |
|
| 3322. |
sigma and rhoare surface and volume charge densities respectively of a charged sphere, so,...... |
|
Answer» `rho=0, sigma=0` |
|
| 3323. |
A uniform meter scale balance s at the 40-cm mark when weihgt of10g and 20g are suspended from the 10-cm and 20-cm marks respectively. The weight of the meter scale is |
|
Answer» 50G |
|
| 3324. |
A particle with rest mass M_0 , splits up into two identical fragments which fly apart in opposite directions at speeds of 0.90c. Find the rest mass of each fragment. |
|
Answer» `m_0=1/2M_0sqrt(1-beta^2)` Substituting the speed we OBTAIN the rest mass of the fragment. |
|
| 3325. |
A magnet is suspended so that it may oscillate in the horizontal plane. It performs 20 oscillation per minute at a place where the angle of dip is30^@ and 15 oscillations per minute , where the angle of dip is 60^@. Compare the earth's total magnetic field at these two places . |
|
Answer» Solution :we known that frequency, `V=(1)/(2PI)sqrt((MB_H)/(I)) or v prop sqrt(B_H) or v prop sqrt(B cos delta)` ` or B? cos delta prop v^(2) or B prop (v^(2))/(cos delta)` `(B_1)/(B_2) = (v_1^(2))/(cos delta_1) xx ( cos delta_2)/(v_2^(2)) = (20 xx 20 xx cos 60^@)/(cos 30^(@) xx 15 xx 15 ) = (16)/(9 sqrt(3))` |
|
| 3326. |
An isolated conducting spherical shell carries a negative charge. What will happe if a positively charged metal object is placed in contact with the shell interior? Assume that the positive charge is (a) less than (b) equal to (c ) greater than the negative charge in magnitude. |
|
Answer» SOLUTION :Net charge will come on the outer surface of the SPHERICAL shell (a) if the positive charge is less than the NEGATIVE on the conducting spherical shell, the net charge will be negative. (B) if the charge is equal to negative charge the net charge is zero. (c ) if the charge is GREATER than the negative charge , net charge is positive |
|
| 3327. |
If you were asked to design a capacitor of small size and large capacitance, what factors would be imperiant in your design? |
| Answer» SOLUTION :AREA, SEPARATION and DIELECTRIC CONSTANT. | |
| 3328. |
The maximum acceleration of a body moving in S.H.M. is a_(0) and maximum velocity is v_(0). The amplitude is given by : |
|
Answer» `(v_(0)^(2))/(a_(0))` `:.""(v_(0)^(2))/(a_(0))=(r^(2)omega^(2))/(omega^(2)r)=r`. THUS correct choice is (a). |
|
| 3329. |
Infra-red spectrum lies between |
|
Answer» RADIO WAVE and microwave region |
|
| 3330. |
Write down the formula for distance between two consecutive bright fringes or two consecutive dark fringes. |
|
Answer» Solution :For fringes of constructive interference (bright), `x_(n)=(nlamdaD)/(d)` for `n^(TH)` ORDER of bright fringe. Now for `(n+1)^(th)` order of bright fringe. `x_(n+1)=((n+1)lamdaD)/(d)` DISTANCE between TWO consecutive bright fringes `x._(n+1)-x._(n)=(2n+3)(lamdaD)/(2d)-(2n+1)(lamdaD)/(2d)` `=(lamdaD)/(2d)[2n+3-2n-1]` `=(lamdaD)/(2d)[2]` `:.beta=(lamdaD)/(d)` Hence, the distance between two consecutiv bright or the distance between two consecutiv dark fringe (s) are same. This is the equation width of fringe also. |
|
| 3331. |
State two characteristic properties of nuclear forces. |
|
Answer» SOLUTION :(i) Nuclear forces are EXTREMELY SHORT range forces. (II) These are charge INDEPENDENT. |
|
| 3332. |
In an induction coil, the coefficient of mutual inductance is 4 henry. If a current of 5 ampere in the primary coil is cut-off in (1)/(1500)s, the e.m.f. at the terminals of the secondary coil will be |
|
Answer» `15kV` |
|
| 3333. |
Graphical soluton of a two body head on collision A block A of mass m moving with a uniform velocity v_(0) strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum. So mv_(0)=mv_(A)mv_(B) (v_(A) and v_(B) are the velocities of the blocks after collision) :. v_(0)=v_(A)+v_(B).........(i) If the collision is perfectly elastic 1/2 mv_(0)^(2)=1/2 mv_(A)^(2)+1/2 mv_(B)^(2) impliesv_(0)^(2)=v_(A)^(2)+v_(B)^(2)......(ii) Both the above equation (i) and (ii) are plotted on v_(A)-v_(B) plane as shown in figure (ii). This plot can be used to find the unknowns v_(A) and v_(B). For example the solution of the situation in figure (i) is v_(A)=0,v_(B)=v_(0) (point y in the plot) Because v_(A)=v_(0), v_(B)=0 (point x in the plot) is not physically possible. If the collision is perfectly inelastic, then the v_(A)-v_(B) plot is |
|
Answer»
|
|
| 3334. |
NAND gate is combination of ….. gate and …….. gate. |
|
Answer» OR, NOT NOT + AND = NAND |
|
| 3335. |
Graphical soluton of a two body head on collision A block A of mass m moving with a uniform velocity v_(0) strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum. So mv_(0)=mv_(A)mv_(B) (v_(A) and v_(B) are the velocities of the blocks after collision) :. v_(0)=v_(A)+v_(B).........(i) If the collision is perfectly elastic 1/2 mv_(0)^(2)=1/2 mv_(A)^(2)+1/2 mv_(B)^(2) impliesv_(0)^(2)=v_(A)^(2)+v_(B)^(2)......(ii) Both the above equation (i) and (ii) are plotted on v_(A)-v_(B) plane as shown in figure (ii). This plot can be used to find the unknowns v_(A) and v_(B). For example the solution of the situation in figure (i) is v_(A)=0,v_(B)=v_(0) (point y in the plot) Because v_(A)=v_(0), v_(B)=0 (point x in the plot) is not physically possible. In a situation block A is moving with velocity 2m//s an strikes another identical block B kept at rest. The v_(A)-v_(B) plot for the situation is shown. m and l are the intersection points whose v_(A), v_(B) coordinaes are given in the figure. The coefficient of restitution of the collision is |
|
Answer» `1/2` |
|
| 3336. |
A ray of light incident at 60^(@) on a prism undergoes a deviation of 20^(@). If the angle of the prism is 40, S.T. the emergent ray is normal to the second face of the prism. |
|
Answer» SOLUTION :`d=(i_(1)+i_(2))-A` `20^(2)=60^(@)+i_(2)-40^(@)` `THEREFORE i_(2)-0`. Hence, emergent ray is normal to the face of the prism. |
|
| 3337. |
A string of linear mass density 4 g/cm is vibrating according to equation - y = A sin (120pit) cos ((2pi)/(5) x) Where x is in centimeters. Find the tension in the string |
| Answer» Answer :A | |
| 3338. |
The long distance transmission of electrical energy is done at |
|
Answer» HIGH POTENTIAL and LOW CURRENT |
|
| 3339. |
Who, according to Mandela is not free? |
|
Answer» oppressor |
|
| 3340. |
On which factors does the self-inductance of a coil depend? |
| Answer» SOLUTION :The self-inductance of a COIL depends on (i) the number of turns per UNIT length of the coil, (II) the length and area of solenoid coil, and (iii) RELATIVE permeability of the core of solenoid coil. | |
| 3341. |
In which orientation, a dipole placed in a uniform electric field is in (i) stable (ii) unstable equilibrium ? |
|
Answer» Solution :A dipole placed in a uniform ELECTRIC FIELD is in a stable equilibrium when angle between `vecp` and `vec E` is `0^@`. (ii) For unstable equilibrium the angle between `vec p and vec E` should be `pi` radian. |
|
| 3342. |
The graph of time period (T) of simple pendulum versus its length (l) is |
|
Answer»
|
|
| 3343. |
If electric field is (a) vec E = 2 a x y hat(i) + a(x^(2) - y^(2)) hat(j) (b) vec(E ) = ay hat(i) + (ax + bz) hat(j) + by hat(k)) Find potential. |
|
Answer» Solution :(a) `DV = -vec(E ). D vec(r ) = -(E_(X) dx + E_(y) dy)` `= - [2 a x y dx + a(x^(2) - y^(2))dy]` `= -[2a x y dx + AX^(2) y - ay^(2) dy]` `int 2a xy dx = 2ay int xdx = 2 ay (x^(2))/(2) = ax^(2) y` `int ax^(2) dy = ax^(2) int dy = ax^(2) y` `2 a x y dx + ax^(2) dy= d (ax^(2) y)` `V = - int vec(E ) . d vec(r ) = - int d(ax^(2) y) - a y^(2) dy` `= - [ ax^(2)y - (ay^(3))/(3)] + C` (b) `dV = -[aydx + (ax + BZ)dy + by DZ]` `= - [a(y dx + xdy) + b(zdy + ydz)]` `-[ad(xy) + bd(yz)]` `V = - int vec(E ) . d vec(r) = - [ int ad(xy) + bd(yz)]` `= -(axy + byz) + C` |
|
| 3344. |
A series combination of a coil of inductance L and a resistor of resistance 12Omega is connected across a 12 V, 50 Hz supply. Calculate L if the circuit current is 0.5 A. |
|
Answer» Solution :Impedance, `Z=(E)/(I)=(12)/(0.5)=24Omega` `and Z=sqrt(R^(2)+OMEGA^(2)L^(2))` `or Z^(2)=R^(2)+omega^(2)L^(2) or L^(2)=(Z^(2)-r^(2))/(omega^(2))` Here `omega=2piv=2xx(22)/(7)xx50` `="314 rads"^(-1) and R=12Omega` `L^(2)=((24)^(2)-(12)^(2))/((314)^(2)) or L=(12sqrt3)/(314)=0.066H` |
|
| 3345. |
Two identical moving coil galvanometers have 10Omega resistance and full scale deflection at 2muA current. One of them is converted into a voltemeter of 100 m V full scale reading and the other into an Ammeter of 1mA full scale current using appropriate resistors. These are then used to measure the voltage and current in the Ohm's law experiment with R =1000Omegaresistor by using an ideal cell . Whichof the following statement (s) is //are correct ? |
|
Answer» The resistance of the Ammeter will be `0.02Omega` (round off to `2^(ND)` decimal place) |
|
| 3346. |
Under what condition the sum and difference of two vectors will be equal magnitude ? |
| Answer» SOLUTION :When TWO vectors are equal in MAGNITUDE and perpendicular to each other. | |
| 3347. |
A simple pendulum is executing simple harmonic motion with a time period T. If thelength of pendulumis increased by 21 %, the % increase in the time period of the pendulum of increased length is : |
|
Answer» 0.1 `:.""T_(2)=(11)/(10)T_(1)` %INCREASE in time PERIOD `=(T_(2)-T_(1))/(T_(1))XX100` `=((11)/(10)T_(1)-T_(1))/(T_(1))xx100=10%`. Correct choice is (a). |
|
| 3348. |
What is considered as a 'Blue Planet' in the poem? |
|
Answer» Mars |
|
| 3349. |
A convex mirror of focal length f forms an image which is (1)/(n) times the object. The distance of the object from the mirror is |
|
Answer» `(N-1)F` |
|
| 3350. |
A sonometer wire resonates with a given tuning fork forming standing waves with three antinodes between the two bridges when a mass of 16 Kg is suspended from the wire. When this mass is replaced by a mass .9 kg. the wire resonates with the same tuning fork for .p. antinodes for the same positions of the bridges. Then .p. is |
|
Answer» |
|