Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3201. |
Two waves of nearly same amplitude, same frequency travelling with same velocity are superimposing to give phenomenon of interference. If alpha_1 and alpha_2be their respective amplitudes, omegabe frequency for both, 'v' be the velocity for both and Delta phiis the phase difference between the two waves then |
|
Answer» the resultant intensity VARIES periodically with time and DISTANCE. |
|
| 3202. |
The de-Broglie wavelength of the electron in the ground state of the hydrogen atom is (radius of the first orbit of hydrogen atom =0.53Å |
|
Answer» `1.67Å` `mvr=(NH)/(2pi)` or `(h)/(MV)=(2pir)/(n) ""...(i)` de-Broglie wavelength `lambda=(h)/(mv) ""...(ii)` From EQS (i) and(ii), we get Wavelength `lambda=(2pir)/(n)` `=(2pxx PI xx0.53Å)/(1)` `=3.33Å` |
|
| 3203. |
Time taken by the sunlight to pass through a slab of thickness 4 mm and refractive index 3 is ........ sec. |
|
Answer» `4 xx 10^(-11)` s `therefore t= (nd)/(c)=(3xx4xx10^(-3))/(3xx10^8)=4xx10^(-11)` s |
|
| 3204. |
A spherical conducting shell of inner radius r_1 and outer radiusr_2has a charge Q. A charge q is placed at the centre of the shell. Find out the surface charge density on the inner and outer surface of the shell. Is the electric field inside a cavity (with no charge ) zero. Independent of the fact wheather the shell is spherical or not ? Explain. |
|
Answer» Solution :When cahrge Q is GIVEN to spherical conducting shell, whole of it spreads uniformaly on the outer surface of shell. Onplacing a charge +q at the centre of the shell , a charge -q is induced on the inner surface of shell and in turn charge +q is induced on its outer surface. ` therefore ` Surfacecharge density of inner surface of the shell. ` "" sigma _("inner")=(-q)/( 4 pi r_1^(2)) ` and Surface charge density of outer surface of the shell. ` "" sigma _("outer")=((Q+q))/( 4 pi r_2^(2)) ` (II) Electric field inside a cavity (with no charge)is ALWAYS zero, whether the shell is spherical or of any other shape. It is accordance with Gauss.s theorem in electrostatics. As charge enclosed by the cavity is zero, hence TOTAL electric flux and consquently ,the field intensity inside a cavity MUST be zero. ` (##U_LIK_SP_PHY_XII_C01_E10_026_S01.png" width="80%"> |
|
| 3205. |
Rain is falling vertically with a speed of 20 ms^(-1)A person is running in the rain with a velocity of 5 ms^(-1)and a wind is also blowing with a speed of 15 ms^(-1). (both from the west). The angle with the vertical at which the person should hold his umbrella so that he may not get drenched is: |
Answer» Solution : `vecV_("rain") =vecV_(R) =20(-hatk)` `vecV_("man") =vecV_(M) =5hati` RESULTANT velocity of rain and wind = `vecV_(RM) =-20vecK + 15hati` Now, Velocity of Rain relative to man= `vecV_(RM) -vecV_(M) = (-20 hatK +15 HATI)-(5hati)` `=-20hatK + 10hati` `tan alpha =1/2 rArr alpha =tan^(-1) 1/2` |
|
| 3206. |
An A.C. of frequency f is flowing in a circuit containing only a choke coil of inductance L. If V_(0) and I_(0) represent the peak values of the voltage and the current respectively, then the average power given by the source to the choke is equal to |
|
Answer» `I_(0)V_(0)//2` `therefore Z=sqrt(R^(2)+4pi^(2)f^(2)L^(2))` `because P = epsilon_(rms)I_(rms)COS phi=epsilon_(rms)I_(rms)(R )/(sqrt(R^(2)+X_(L)^(2)))` For idea CHOKE coil, `cos phi = 0` and R = 0 `therefore P = 0` |
|
| 3207. |
The thermo emf of a hypothetical thermocouple varies with the temperature 0 of hot junction as E = atheta + btheta^2 in volts, where the ratio a/bis 700^@c. If the cold junction is kept at 0^@c, then the neutral temperature is |
|
Answer» `700^@c` `P=(dE)/(dtheta) =(d(atheta + btheta^(2)))/(dtheta) =a+2btheta` At, Neutral temperature, `theta=t_(n)`, P becomes zero `a+2bt_(n)=0` `THEREFORE t_(n)=- a/(2b) = - a/b . 1/2` `=-700. 1/2 `[Given, `a/b=700^@C]` `-350^@C` Option not available |
|
| 3208. |
Net capacitance of three identical capacitors in series is 1 muF. What will be their net capacitance if connected in parallel ? Find the ratio of energy stored in the two configurations if they are both connected to the same source. |
|
Answer» Solution :It is given that `C_1 = C_2 =C_3 =C` (SAY) Then their equivalent capacitance in series `C_s = C/3 =1 MU F` `rArr C = 3muF` `:.` Net capacitance in parallel arrangement `C_p = 3C = 3 xx 3 muF = 9 muF` Let the capacitor combination be CONNECTED, in both configurations, to a given source of voltage V. Then net energy stored in series combination `u_s = 1/2 C_s.V^2` and net energy stored in parallel combination `u_p = 1/2 C_p V^2 rArr u_s/u_p = C_s/C_p = (1 muF)/(9muF) =1/9`. |
|
| 3209. |
A circuit contains an ideal battery , three resistors, and tow ideal ammeters. The ammeters read 0.2 A and 0.3 A. After two of the resistors are switched, the readings of the ammeters did not change. Find the battery current. |
|
Answer» If `R_2 = R_1, I_1 = I_2 = 0.15 A` and `I_3 = 0.05A`. As the ammeters are ideal, we can conclude that the three resistors `R_1, R_2, and R` are actually CONNECTED in parallel, the equivalent resistance being `R_(EQ) = (R_1R_2R_3)/(R_1R_2+R_1R_3 + R_2R_3)` In the figure, the electric CURRENTS on each resistors and battery are shown. The readings of the two ammeters are different and, consequently, by SIMPLE symmetry considerations, resistors `R_1 and R_3` are NECESSARILY different. In other words, if we interchange `R_1 and R_3`, the readings of the ammeters will also be interchanged. Therefore, we have two possible alternatives. `R_2= R_1` (if resistors `R_2 and R_1` switched, the readings of the ammeters do not vary) or `R_2 = R_3 (R_2` and `R_3` can be switched and the ammeters do not change.) The two solutions are : If `R_2 = R_1` we obtain `I_2 = I_3 = 0.1A` and `I_1 = 0.2A`, and the battery current is `I = 0.4A`. |
|
| 3210. |
A wire carrying a current of 125 A is bent into the form of a circle of radius 5 cm. Calculate the flux density at the centre of the coil. |
| Answer» SOLUTION :`157 XX 10^(-5) Wb//m^2` | |
| 3211. |
Two concentric cyclinder have radii a and 2a. The charges on the cyclinders are +q and -q respectively. Two dielectric, each filling half the cyclinder length-wise is introduced in between the cyclinders. The dielectric constants are K and K/2.The capacitance of the arrangement (consider the innermost and outermost points) is |
|
Answer» `(piLepsi_(0)K)/(l n 2)` |
|
| 3212. |
The velocity with which a projectile must be fired so that it escapes earth's gravitation, does not depend on : |
|
Answer» mass of the earth It is INDEPENDENT of the mass of the body to be ESCAPED. Thus correct choice is (c ). |
|
| 3213. |
There is a small hole in a table. A string of length lm passes through it. Two bodies of masses 70g and 100 g are attached at its ends. The lOOg mass hangs freely at a depth of 60 cm from the table. If this mass is to be in equilibrium, the other mass should rotate in a circle with a frequency equal to |
|
Answer» `(4PI//140)` HZ |
|
| 3214. |
An external harmonic force F whose frequency can be varied, with amplitude maintained constant, acts in a vertical direction on a ball suspended by a weightless spring. The damping coefficient is eta times less than the natural oscillation frequency omega_(0) of the ball. How much, in per cent, does the mean power ( :P: ) developed differ from themaximum mean power ( :P: )_(max)? Averaging is performed over one oscillation period. |
|
Answer» Solution :Given ` beta = omega_(0)//eta` . Then from the previous problem `lt Pgt =(F_(0)^(2)omega_(0))/( etam). (1)/( ((omega_(0)^(2))/(OMEGA)-omega)^(2)+ 4 ( omega_(0)^(2))/( eta^(2)))` At displacement resonance ` omega=sqrt(omega_(0)^(2)-2 beta^(2))` `lt P gt_(res)=(F_(0)^(2)omega_(0))/( etam)(1)/((4 beta^(4))/( omega_(0)^(2)- 2 beta^(2))+(4 omega_(0)^(2))/( eta^(2)))=(F_(0)^(2)omega_(0))/( eta m)(1)/((4 omega_(0)^(4)//eta^(4))/( omega_(0)^(2)(1-(2)/( eta^(2))))+4( omega_(0)^(2))/( eta^(2)))` `=(F_(0)^(2))/( 4 eta m omega_(0))(n^(2))/((1)/( n^(2)-2)+1)=(F_(0)^(2)eta)/( 4 m omega_(0))(n^(2)-2)/( n^(2)-1)` while `lt P gt_(MAX)=(F_(0)^(2)eta)/(4 m omega_(0))`. THUS `(lt P gt_(max)- lt P gt _(res))/(lt P gt_(max))=(100)/(eta^(2)-1)%` |
|
| 3215. |
Both mass and charge are scalars and hence got the additive property. However, in adding charges it is not enough to just add the amount of charges. Why? |
| Answer» Solution :Unlike mass, CHARGES are of TWO DIFFERENT kind, positive and negative. | |
| 3216. |
Ifthe length of a cylinder is measured to be 50 cm with an error of 0.25 cm. The percentage error in the measured length is |
|
Answer» `0.4%` |
|
| 3217. |
The passenger of example slept with his head towards the engine and feet towardsthe guard's coach. If he measured 6 ft in the train frame, how tall is he in the ground frame ? |
|
Answer» Solution :In the ground frame, the passanger is moving with a velocity c / 10 . His length is thus contacterd. Thelength measured in the train frame is the rest length of the passenger as the passenger is at rest in the train. Thus , his length in the ground frame is ` L' = 6 FT (SQRT 1 - (1 / 10 )^(2)) =6 ft (sqrt 99 / 100 ) = 5 FEET 11.6 inches`. |
|
| 3218. |
Three chargesq,-2q andqareplacedatthreevertices ofanequilateraltriangle.Determinethe equivalentdipolemomentof the system. |
Answer» Solution :The givensystemisacombination at twodipolesat an angle` 60 ^@ `with eachother. Letthe dipole moment of onedipoleis`p _ 1`and thatofanotherdipolesis` p _ 2` , thelengthof eachside of theequilateraltriangleisa. `THEREFORE ` Equivalentdipolemoment, ` p =p _ 1cos 30 ^@+p _ 2COS 30^@` [` because ` since COMPONENTS canceleachother ] `= 2qa cos 30 ^@ ""[ becausep _ 1=p _ 2= qa ]` `=2q axx( SQRT3 ) /( 2 )=sqrt 3 qa ` |
|
| 3219. |
Match the following |
Answer» SOLUTION :
|
|
| 3220. |
You are given a 2 mu F parallel plate capacitor. How would you establish an instantaneous displacement current of 1mA in the space between its plates ? |
|
Answer» Solution :Charge on PLATE, q = CV `I_(d)dt=CdV` `therefore I_(d)=C(dV)/(dt)` `therefore (dV)/(dt)=(I_(d))/(C )=(10^(-3))/(2xx10^(-6))` `therefore (dV)/(dt)=500(V)/(s)` By APPLYING variable p.d. of `500(V)/(s)` we can obtain displacement CURRENT of desired value. |
|
| 3221. |
In a.c. circuits, the a.c. meters measure the : |
|
Answer» MEAN values |
|
| 3222. |
A resistance R and a capacitor C are joined to a source of ac of constant emf and variable frequency. The potential difference across C is V. If the frequency of ac is gradually increased, V will |
|
Answer» INCREASE |
|
| 3223. |
State Brewster's law . Show that the reflected and refracted rays are normal to each other at the polarising angle of incidence. |
Answer» SOLUTION :The tangent of the polarising angle is equal to the refractive INDEX of the medium.  From Brewster.s law `n=tanthetap=(sintheta_(p))/(costheta_(p))=(sintheta_(p))/(cos(90-theta_(p)))`……………..`(1)` From Snell.s law `n=(sini)/(cosr)=(sintheta_(p))/(cosr)`.............`(2)` From `(1)` & `(2)` we GET `sin(90-thetap)=SINR` `90-thetap=r` or `thetap+r=90^(@)` But angle `MON=180^(@)`, Hence reflected and reffracted rays are PERPENDICULAR. |
|
| 3224. |
Two coils are placed closed to each other. The mutual inductance of the pair of coils depends upon ........ |
|
Answer» the rates at which currents are changing in TWO coils |
|
| 3225. |
Draw a graph showing variation of induced emf over a cycle in an ac generator. Also indicate peak value of emf. |
| Answer» SOLUTION :DISC THROWN up in to AIR. | |
| 3226. |
A student performs the melde's experiment in parallel and perpendicular position and draws the conclusion . A) number of loops in perpendicular position is equal to twice the number of loops in parallel position B) the wavelength in perpendicular position is equal to twice the wave lengthof the wave in parallel position C) of the period of the wave on the string in parallel position D) the ratio of frequency of vibrating string in parallel to perpendicular position is 2:1 The correct statement is / are |
| Answer» Answer :B | |
| 3227. |
A closely wound solenoid of 800 turns and area of cross section 25 xx 10^(-4)m^(2) carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment? |
|
Answer» Solution :Current carrying solenoid ACTS like a bar magnet placed on its axis with `overset(to) (m) bot overset(to) (A)` (where `overset(to) (A) =` area vector of cross-section of current carryingsolenoid). Now, magnetic dipole moment of current carrying solenoid is given by, `overset(to) (m_(s) ) = NIoverset(to) (A) ""...(1)` `therefore m_(s) = NIA ""...(2)` `therefore m_(s) = (800) (3) (2.5 XX 10^(-4) )` `therefore m_(s) = 0.6 J//T (= Am^(2) )""...(3)` Here direction of `overset(to) (A)` is determined from the sense of current by using LAW of right handed screw.  Here, magnetic fields produced by coaxial current carrying solenoid and bar magnet shown in above figure have same patterns. |
|
| 3228. |
The objective lens of a compound microscope produces magnification of 10. In order to get an over all magnification of 100 when image is formed at 25 cm from the eye, the focal length of the cye lens should be in cm) |
|
Answer» 4 |
|
| 3229. |
The first excitation potential of given atom is 10.2 eV. Then the ionization potential must be: |
|
Answer» 20.4 V |
|
| 3230. |
Determine the value of the current in the solenoid so that the magnetic field at the center of the loop is zero tesla. |
|
Answer» `1.4xx10^(-1)`A |
|
| 3231. |
A charged particle with a velocity 2xx10^(3)ms^(-1) passes undeflected through electric field and magnetic fields in mutually perpendicular directions. The magnetic field is 1.5T. The magnitude of electric field will be: |
|
Answer» `1.5xx10^(3)NC^(-1)` or `EV B sin theta =eE` Given `v=2xx10^(3) ms^(-1)` `B=1.5T` and `theta=90^(@)` HENCE `E=v B sin theta` `=2xx10^(3)xx1.5 sin 90^(@)` `=3xx10^(3)V//m` |
|
| 3232. |
The mass of a lift is 500 kg. What will be the tension on it's cable when it is going up with an acceleraion 20m/s^2 |
|
Answer» 5000 N |
|
| 3233. |
A horizontal force applied on a body on a rough horizontal surface produces an acceleration 'a'. If co-efficient of friction between the body & surface which is m is reduced to m/3, the acceleration increases by 2 units. The value of m is |
|
Answer» 2/3 G |
|
| 3234. |
Find the percent increase in the magnetic field B when the space within a current-carrying toroid is filled with aluminium. The susceptibility of aluminium is 2.1 xx 10^(-5) |
|
Answer» Solution :In ABSENCE of aluminium, the magnetic field is `B_(0) = μ_(0)H` .As the space INSIDE the toroid is filled with aluminium, the field becomes `B=mu_(H)=mu_(0)(1+chi)H` The percent increases is `(B-B_(0))/(B_(0))xx100=(mu_(0)chiH)/(mu_(0)H)xx100` `=chixx100=2.1xx10^(-3)` |
|
| 3235. |
A string of length 0.4m and mass 10^(-2)kg is tightly clamped at its ends. The tension in the string is 1.6N..Identical wave pulses are produced at one. end al equal intervals of time Deltat - The minimum value of Deltat , which allows constructive interferenceIf between successive pulses is |
|
Answer» 0.05 s |
|
| 3236. |
A rat is running on ice with speed v=pims^(-1). Suddenly he decides to turn by 90^(@) and want of keep running with the same speed throughout. What is the least amount of time (in seocnds) he needs for such a turn? Suppose that rat's feet can move independently. Coefficieny of friction between rat's feet and ice is 0.125. ("Given : "pi^(2)=g) |
|
Answer» |
|
| 3237. |
Three charges Q, +q and +q are placed at the vertices of a right angle triangle (isosceles triangle) as shown. If the net electrostatic potential energy of the configuration is zero, value of Q is |
|
Answer» `(+Q)/( 2 +SQRT(2))` |
|
| 3238. |
An unpolarized beam of light has intensity I_(0) . It is incident on to ideal polarizing sheets . The angle between the axes of polarization of these sheets is theta . Find theta ifthe emerging light has intensity I_(0)//4) |
|
Answer» `sin^(-1)(1//2)` |
|
| 3239. |
Let vecF be the force acting on a particle having position vector vecrandvectau be the torque of this force about the origin. Then : |
|
Answer» `vecr.vectau=0 and vecF.vectau=0` Now, `vecr.vectau=vecr.(vecFxxvecr)=R(FR)COS90^(@)`= Zero. Similarly `vecF.vectau` = zero |
|
| 3240. |
Same current i=2 A is flowing in a wire frame as shown in the figure. The frame is a combination of two equilateral triangles ACD and CDE of side 1 m. It is placed in uniform magnetic field B=4 Tacting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is |
|
Answer» 24 N |
|
| 3241. |
The colours that one sees when a CD is viewed is due to ____effects. |
| Answer» SOLUTION :DIFFRACTION | |
| 3242. |
The inverse square law in electrostatic is |F|=(e^(2))/((4pi epsi_(0))*r^(2)) for the force between an electrona nd a proton. The ((1)/(r)) dependence of |F| can be understood in quantum theory as being due to the fact that the particle of light (photon) is massless. If photons had a mass m force would be modified to |F|=(e^(2))/((4pi epsi_(0))r^(2))[(1)/(r^(2))+(lambda)/(r)] exp(-lambdar) where lambda=(m_(p)c)/(h) and h=(h)/(2pi). Estimate the change in the ground state energy of a H-atom if m_(p) were 10^(-6) times the mass of an electron |
|
Answer» SOLUTION : As per the statemen, `lambda=(m_(p)c)/(h)=(2pi m_(p)c)/(h)=(2pi (10^(-6)m_(e))c)/(h)` `:. Lambda=(2xx3.14xx10^(-6)xx9.1xx10^(-31)xx3xx10^(8))/(6.625xx10^(-34))` `:. Lambda=2.588xx10^(6)m^(-1)...(1)` Note here `lambda=(m_(p)c)/(h)` is not wavelength but it is only constant. (Because its unit in `m^(-1))`. Now Bohar radius `r_(B)=0.53Å=5.3xx10^(-11)m` `:. lambda gt gt r_(B) ...(2)` ACCORDING to statement, `|vecF|=(e^(2))/(4pi epsi_(0)) ((1)/(r^(2))+(lambda)/(r))e^(-lambdar) ....(3)` Since `vecF` is a CONSERVATIVE force, `|vecF|=(dU)/(dr)` `:.dU=|vecF|dr` `:.U= int|vecF|dr= int (e^(2))/(4pi epsi_(0))((1)/(r^(2))+(lambda)/(r))e^(-lambdar)dr ....(4)` Suppose `x=(e^(-lambdar))/(r)=(1)/(r)xxe^(-lambdar)` `:.(dx)/(dr)=(1)/(r) (e^(-lambdar)) (-lambda)+e^(lambda-r)(-(1)/(r^(2)))` `:.dx=(-(lambda)/(r)e^(-lambdar)-(e^(-lambdar))/(r^(2))dr` `:.dx=-((lambda^(-lambdar))/(r)+(e^(-lambdar))/(r^(2)))dr` `rArr int (lambdae^(lambda-r))/(r)+(e^(-lambdar))/(r^(2))-dr=- intdx=-x=-(e^(-lambdar))/(r)....(5)` From equation (4) and (5), `U=(e^(2))/(4pi epsi_(0))(-(e^(-lambdar))/(r))` `:.U-(e^(2))/(4pi epsi_(0))((e^(-lambdar))/(r))....(6)` Now, according to Bohr.s first postulate, for n=1 `mvr=(h)/(2pi)` `:.v=(h)/(2pi mr)....(7)` Here `F=(e^(2))/(4pi epsi_(0))((1)/(r^(2))+(lambda)/(r))e^(-lambdar)` `:.(MV^(2))/(r)=(e^(2))/(4pi epsi_(0))((1)/(r^(2))+(lambda)/(r)) ( :. e^(-lambdar)~~1)` `:. (m)/(r)xx(h^(2))/(4pi^(2)m^(2)r^(2))=(e^(2))/(4pi epsi_(0))((1)/(r^(2))+(lambda)/(r))` [ From equation (7)] `:. (h^(2))/(4pi^(2)mr^(3))=(e^(2))/(4pi epsi_(0))((1)/(r^(2))+(lambda)/(r))` `:.(h^(2))/(4pi^(2)m)=(e^(2))/(4pi epsi_(0))(r+lambdar^(2)) ...(8)` Since no radiation is emitted for `r=r_(B)`, taking `lambda=0` from above equation `m_(p)=0` `(h^(2))/(4pi^(2)m)=(e^(2))/(4pi epsi_(0))(r_(B)) .....(9)` Comparing equation (8) and (9), `r_(B)=r+lambda r^(2).....(10)` Suppose `r=r_(B)+dr ....(11)`(where dr is diffrentially small) Now, `(e^(-lambdar))/(r)=(e^(-lambda(r_(B)+dr)))/(r_(B)+dr)` `=(1)/(r_(B)+dr){1-lambda (r_(B)+dr)}` `=(1-lambdar_(B)-lambdadr)/(r_(B)+dr)` `~~(1-lambda r_(B))/(r_(B)(1+(dr)/(r_(B)))) ( :. lambda dr` is negligible) `:.(e^(-lambdar))/(r)=((1-lambdar_(B))/(r_(B)))(1+(dr)/(r_(B)))^(-1)` `=((1-lambdar_(B))/(r_(B)))(1-(dr)/(r_(B)))` `=(1-lambdar_(B))((1)/(r_(B))-(dr)/(r_(B)^(2)))` `=(1-0)((1)/(r_(B))-0)` `( :. lambdar_(B) lt lt TL lt 1 and (dr)/(r_(B)^(2))` is negligible) `=(1)/(r_(B)) ....(12)` From equation (6) and (12), `U=-(e^(2))/(4pi epsi_(0))((1)/(r_(B)))` `=-(ke^(2))/(r_(B))( :. k=(1)/(4 pi epsi_(0)))` `=-((9xx10^(9))(1.6xx10^(-19))^(2))/((0.53xx10^(-10))` `=-4.374xx10^(10-38+10)J` `=-4.374xx10^(-18)J` `:.U=-(4.374xx10^(-18))/(1.6xx10^(-19))eV` `=-2.717xx10^(1)eV` `:.U=-27.17eV` In the present, case, kinetic energy of electron `K=(1)/(2)mv^(2)=(1)/(2)m((h^(2))/(4pi^(2)m^(2)r^(2)))` [ from equ. (7)] `:.K= (h^(2))/(8 pi^(2)mr^(2))` `=(h^(2))/(8pi^(2)m(r_(B)+dr)^(2))` `=(h^(2))/(8pi^(2)m{r_(B)(1+(dr)/(r_(B)))}^(2))` `=(h^(2))/(8pi^(2)mr_(B)^(2))(1+(dr)/(r_(B)))^(-2)` `:.K=(h^(2))/(8 pi^(2)mr_(B)^(2))(1-(2dr)/(r_(B)))....(14)` (According to binomial theorem) From equation `(10),r_(B)=r+lambdar^(2)` But according to equation (11), `r=r_(B)+dr` and so `r_(B)=r_(B)+dr+lambda(r_(B)+dr)^(2)` `:.0=dr+lambdar_(B)^(2)+2lambdar_(B)dr+lambda dr^(2)` `:. 0~~ dr+lambdar_(B)^(2)` `( :.2lambdar_(B)dr and lambda dr^(2)` are negligible here) `:.dr =-lambda_(B)^(2)....(15)` From equation (14) and (15) `K=(h^(2))/(8pi^(2)mr_(B)^(2)){1-(2)/(r_(B))(-lambda_(B)^(2))}` `:.K=(h^(2))/(8pi^(2)mr_(B)^(2))(1+2lambdar_(B))` `:.K=13.6(1+2lambdar_(B))....(16)` `( :. (h^(2))/(8pi^(2)mr_(B)^(2))=13.6eV)` Adding equation (13) and (16), total energyin final condition, `E_(f)=13.6(1+2lambdar_(B))-27.2eV` but `E_(i)=-13.6eV` Required change of total energy, `DeltaE=E_(f)-E_(i)` `=13.6(1+2lambdar_(B))-27.2-(-13.6)` `=13.6(1+2lambdar_(B))-13.6` `=13.6+27.2lambdar_(B)-13.6` `:.DeltaE=27.2lambdar_(B)eV` |
|
| 3243. |
In what kind of AC circuit, the current lays behind the voltage ? |
| Answer» Solution :In AC CIRCUIT containing PURE inductance. | |
| 3244. |
State Gauss's law. Derive an expression for electric intensity at a point outside the uniformly charged shell. |
Answer» Solution :Gauss.s theorem: "The total outward electric flux passing through a closed surface in air is `(1/epsilon_0)` times the total charge enclosed by it..  Let +Q. be the charge enclosed by a hollow conductor of RADIUS .R.. Let .p. be a point at a distance .r. from the centre of the conductor Let .ds be a small element of area SURROUNDING the point. A normal drawn from the point coincides with the direction of E. HENCE cos `0^@=1`. From Gauss. theorem, `TOEF=phi=(1/epsilon_0)Q` ...(1) by definition `phi=E cos theta sum ds`. where `sumds=4pir^2 , cos theta=cos 0^@ =1` Hence , `phi=E. 4pir^2` ...(2) Comparing (1) and (2) we write `E=(1/(4piepsilon_0))Q/r^2` For a point on the surface , r =R . `E=(1/(4piepsilon_0))(Q/R^2)` . This electric field INTENSITY is maximum. Since electric flux depends on the charge enclosed, and electric field intensity depends on the electric flux, electric field remains ZERO at all points inside the spherical hollow conductor. |
|
| 3245. |
For the circuit shown in figure, determine the voltage across 4Omega resistors in volt ? |
|
Answer» |
|
| 3246. |
The pair of equations x = a and y =b graphically represents lines which are |
|
Answer» Parallel |
|
| 3247. |
Consider the situation shown in figure. The plates of the capacitor have plate area 1A = lb1 and are clamped in the laboratory. The dielectric slab is released from rest with length a inside the capacitor. Neglecting any effect of friction or gravity, show that the slab will execute periodic motion and find its time period. |
|
Answer» |
|
| 3248. |
The work function of cesium metal is 2.14 eV .When light of frequency 6 xx 10^(14) Hz is incident on the metal surface.phtoemission of electrons occurs. What is the : (a) maximum kinetic energy of the emitted electrons, (b) stopping potential , and (c) maximum speed of the emitted photo - electrons ? |
|
Answer» SOLUTION :Here, `phi_(0) = 2.14 eV, upsilon = 6 xx 10^(14) Hz` (a) `K_(max) = hupsilon-phi_(0) = 6.63 xx10^(-34) xx 6 xx 10^(14 )J -2.14 eV` `= (6.63 xx 6 xx 10^(-20))/(1.6 xx 106(-19)) eV - 2.14 eV` `= 2.48 - 2.14 = 0.34 eV` (b) As `eV_0 = K_(max) = 0.34 eV` `:.` Stopping potential `V_0 = 0.34eV` (c) `K_(max) = 1/2 mv_(max)^2 = 0.34 eV` `= 0 .34 xx 1.6 xx 10^(-19) J` or `v_(max_^(2) = (2 xx 0.34 xx 1.6 xx 10^(-19))/m` ` = (2xx 0.34 xx 1.6 . 10^(-19))/(9.1 xx 10^(-31)) = 119560 .4 xx10^(6)` or `v_(max) = 345.8 xx 19^(3) ms^(-1) = 345 .8 kms^(-1)` |
|
| 3249. |
In an intrinsic semiconductor the energy gap E_(g) is 1.2eV. Its hole mobility is much smaller than electron mobility and independent of temperature. What is the ratio between conductivity at 600K and that at 300K ? Assume that the temperature dependence of intrinsic carrier concentration n_(i) is given by n_(i)=n_(0)"exp"(-(E_(g))/(2k_(B)T)) where n_(0) is a constant. |
|
Answer» Solution :Suppose `n_(i)=n_(0)"exp"(-(E_(g))/(2k_(BT)))` Here, `n_(0)` is constant. Conductivity of semiconductor `sigma=e(n_(e )mu_(e )+m_(H)mu_(h))` `therefore sigma=n_(i)e(mu_(e )+mu_(h))` (`because` For intrinsic semiconductor `n_(i)=n_(e )=n_(h)`) and the mobility of the electrons is much higher than that of the mobility of hole, means `mu_(e ) gt gt mu_(h)` `therefore sigma=n_(i)e mu_(e )` but `n_(i)=n_(0)"exp"[(-Eg)/(2k_(B)T)]` is given. `therefore sigma=n_(0)"exp"[(-Eg)/(2K_(B)T)]e mu_(e )` but `e mu_(e )n_(0)` in independent to temperature hence putting constant `sigma_(0)` for it. `sigma=sigma_(0)"exp" [(-Eg)/(2k_(B)T)]` `therefore` At `T_(1)=600K, sigma_(1)=sigma_(0)"exp"[(-Eg)/(2k_(B)T_(1))]` and at `T_(2)=300K, sigma_(2)=sigma_(0)"exp"[(-Eg)/(2k_(B)T_(2))]` `therefore (sigma_(1))/(sigma_(2))=("exp"[(-Eg)/(2k_(B)T_(1))])/("exp"[(-Eg)/(2k_(B)T_(2))])="exp"[(Eg)/(2k_(B)){(1)/(T_(2))-(1)/(T_(1))}]` `="exp"[(1.2)/(2xx8.62xx10^(-5)){(1)/(300)-(1)/(600)}]` `="exp"[(0.6xx10^(5))/(8.62)xx(1)/(600)]` `therefore (sigma_(1))/(sigma_(2))="exp"(11.6)` `=e^(11.6)` `=(2.718)^(11.6)` `"LOG"(sigma_(1))/(sigma_(2))=11.6log(2.718)` `=11.6xx0.4343` `=5.1247` Antilog of 0.1247 `therefore (sigma_(1))/(sigma_(2))=1.1332 xx 10^(5)` `~~1.1xx10^(5)` Therefore, the ratio between the conductivities is `1.09xx10^(8)`. The ratio shows that conductivity of semiconductor increases rapidly with temperature. |
|
| 3250. |
A coherent beam light of intensity I and absolute wavelength lambda= 5000Å is being incident on the slits making an angle 30^@ with horizontal. If screen is placed at a distance D=1 m from the slits and the separation between- the slits is 3 xx 10^(-4) m. A thin film of glass mu_(g)= 3/2 and thickness 0.41 mm is placed near one slit as shown in the figure, find (a) the position of central maxima. (b) the intensity at'point O. |
|
Answer» SOLUTION :Let central amxima lies at a point P at a distance x from the central line. Then optical path diffenrece `Delta`p at a point P is: `(S_(2)P - t) + tmu_(g) - mu_(w)dsintheta - S_(1)p` `implies S_(2)P - S_(1)P + (mu_(g) -1) t - mu_(w)dsintheta` `implies (xd)/D + (mu_(g) -1 )t - mu_(w)dsintheta` For central maxima `Deltap=0` `x=D/d[(mu_(w)dsintheta) - (mu_(g)-1)t]` `1/(3xx10^(-4)) [4/3 xx3 xx10^(-4) xx 1/2 -0.5 xx 0.41 xx10^(-3)]` `= (5xx10^(-6))/(3xx10^(-4)) = -1.66xx10^(-2)m=-1.66m` So central maxima lies at a distance 1.66 cm below the central line (b) At POINTO , optical path difference is `(mu_(g)-1)t - mu_(w)dsintheta=-5xx10^(-6)m` So intensity at 0, `I_(0) =I + I + 2sqrt(II) "cos" (2pi)/(5xx10^(-7))(-5xx10^(-6))=4I` 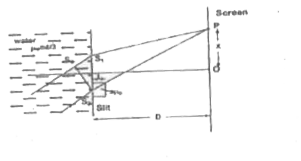
|
|