Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 39451. |
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror. |
|
Answer» SOLUTION :Here, `f=4.5 cm, u=-12 cm` and f= + 15 cm, hence as per MIRROR formula `1/v+ 1/u = 1/f`, we have `1/v =1/f -1/u =1/(+15) =1/15 + 1/12 = (4+5)/60 = 9/60 = 3/20 rArr v=+20/3 cm = + 6.7 cm` Again, `m=h^(.)/h =-v/u`, hence, `h. =-v/u xx h =-(6.7)/(-12) xx 4.5 = +2.5 cm` and magnification `m=h^(.)/h = (2.5 cm)/(4.5 cm) = 0.55` As the needle is MOVED farther from the mirror, the image moves from the side of pole towards (but NEVER beyond) the principal focus of the mirror. Moreover, magnification `m to 0` |
|
| 39452. |
If an electron and a photon propagate in the form of waves having the same wavelengths,it implies that they have same : |
|
Answer» Energy |
|
| 39453. |
Electric charges q, q, -2q are placed at the corners of an equilateral triangle ABC of side 1. The magnitude of electric dipole moment of the system is |
| Answer» Answer :C | |
| 39454. |
Electric potential inside hollow charged sphere of radius .r. is ______ [k = (1)/(4pi epsilon_(0))] |
|
Answer» zero |
|
| 39455. |
If I_(1), I_(2) and l_3 are wave lengths of the waves giving resonance with fundamental, first and second over tones of closed organ pipe. The ratio of wavelengths I_(1): I_(2) : I_(3) is……………… |
|
Answer» `1:2:3` |
|
| 39456. |
The focal length of a converging lens is measured for violet, green and red colours. If is f_(v), f_(G) and f_(R) respectively. We will get |
|
Answer» `f_(v) = f_(G)` |
|
| 39457. |
The radionuclide " "^(11)C decays according to " "_(6)^(11)C (to) " "_(5)^(11)B + e^(+) +nu : T_(1/2) = 20.3min The maximum energy of the emitted positron is 0.960 MeV. Given the mass values: m(" "_(6)^(11)C) =11.011434u and m(" "_(6)^(11)B) = 11.009305u, Calculate Q and compare it with the maximum energy of the positron emitted. |
|
Answer» Solution :Q-value=[`" "^(m)N(" "^(11)C)-{m_(N)(" "^(11)B) + me} ]u XX 931.5 MeV = [{m(" "_(6)^(11)C) -6m_(e)}-{m(" "_(5)^(11)B)-5 m_(e) + m_(e)}]u xx 931.5 MeV=[ m(" "_(6)^(11)C) - m(" "_(5)^(11)B) - 2m_(e)]u xx 931.5 MeV= [11.011434 -11.009305 - 2 xx 0.000548] xx 931.5 MeV = 0.961 MeV` The maximum energy of the positron (0.960 MeV) is ALMOST equal to Q-value. |
|
| 39458. |
You are supplied with a 1m long uniform resistance wire of resistance 3Ω and a cell of emf 1.5v.How can you modify above arrangement to mea sure a p.d. in the range 0-1mV with a least count of 0.15mV. |
| Answer» SOLUTION :To get least COUNT of 0.15mV, 10M WIRE has to be USED | |
| 39459. |
Two particles moving in a laboratory frame of reference along the same straight line with the same velocity v=(3//4)c strike against a stationary target with the time interval Deltat=50ns. Find the proper distance between the particles prior to their hitting the target. |
|
Answer» SOLUTION :In the frame K in which the particles are at rest, their positions are A and B whose coordinates may be taken as, `A: (0, 0, 0), B=(l_0, 0, 0)` In the frame `K^'` with RESPECT to which K is moving with a velocity v the coordinates of A and B at TIME `t^'` in the moving frame are `A=(vt^', 0, 0) B=(l_0sqrt(1-beta^2)+vt^',0,0), beta=v/c` Suppose B hits a stationary target in `K^'` after time `t_B^'` while A hits it after time `t_B+Deltat`. Then, `l_0sqrt(1-beta^2)+vt_B^'=v(t_B^'+Delta t)` So, `l_0(vDelta t)/(sqrt(1-v^2//c^2))` 
|
|
| 39460. |
The dimensions of intensity of wave are : |
|
Answer» `[ML^(2)T^(-3)]` `=("ENERGY")/("areaxxtime")=(ML^(2)T^(-2))/(L^(2)T)=[ML^(0)T^(-3)]` Hence correct choice is `(b)`. |
|
| 39461. |
The p-n junction diode is used as |
|
Answer» an amplifier |
|
| 39462. |
Explain in detail the effect of a dielectric placed in a parallel plate capacitor. |
|
Answer» Solution :(i) When the capacitor is disconnected from the battery: Consider a capacitor with two parallel plates each of cross - SECTIONAL area A and are separated by a distance d. The capacitor is charged by a battery of voltage `V_(0)` and the charge stored is `Q_(0)` . The capacitance of the capacitor without the dielectric is `C_(0)= (Q_(0))/(V_(0))` The battery is then disconnected from the capacitor and thedielectric is inserted between the plates . The introduction of dielectric between the plates will decrease the electric field . Experimentally it isfound that the modifed electric field is given by `E = (E_(0))/(epsilon_(0))` 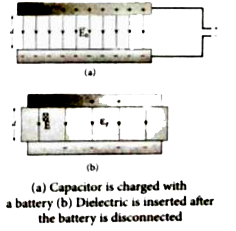 Here `E_(0)`is the electric field inside the CAPACITORS when there is no dielectric and `epsilon_(r)` is the relative permeability of the dielectric or simply known as the dielectric constant . Since `epsilon_(r) gt 1` the electric field `E lt E_(0)` . As a result the electrostatic potential difference between the plates ( V - Ed) is also reduced . But at the same time the charge `Q_(0)` will remain constant one the battery is disconnected. Hence the new potential difference is `V =Ed = (E_(0))/(epsilon_(0)) d = (V_(0))/(epsilon_(r))` We know that capacitance is inversely proportional to the potential difference . Therefore as V decreases C increases . Thus new capacitance in the presence of a dielectric is `C = (Q_(0))/(V) = epsilon_(0) (Q_(0))/(V_(0)) = epsilon_(r) C_(0)` Since `e_(r) gt 1` we have `C gt C_(0)` . Thus insertion of the dielectric `epsilon_(r)` increases the capacitance . Using equation . `C= (epsilon_(0)A)/(d) ` `C= (epsilon_(r)epsilon_(0)A)/(d) = (epsilonA)/(d)` where `epsilon= epsilon_(r)epsilon_(0)` is the permittivity of the dielectric medium . The energy stored in the capacitor before the insertion of a dielectric is given by `U_(0)=(1)/(2) (Q_(0)^(2))/(C_(0))` After the dielectric is inserted the charge `Q_(0)` REMAINS constant but the capacitance is increased . As a result the stored energy is decreased . `U = (1)/(2) (Q_(0)^(2))/(2C) =(1)/(2) (Q_(0)^(2))/(2epsilon_(r)C_(0))= (U_(0))/(epsilon_(r))` Since `epsilon_(r) gt 1 ` we GET `U lt U_(0)` . There is a decrease in energy because when the dielectric is inserted the capacitor spends some energy in pulling the dielectric inside . (ii) When the battery remains connceted to the capacitor : Let us now condsider what happens when the battery of voltage `V_(0)` remains connceted to the capacitor when the dielectric is inserted into the capacitor . The potential difference `V_(0)` across the plates remains constant . But it is found experimentally ( first shown by Faraday ) that when dielectric is inserted the charge stored in the capacitor is increased by a fatcor `epsilon_(r)` . `Q= epsilon_(r) Q_(0)` Due to this increased charge the capacitance is also increased . The new capacitance is `C= (Q)/(V_(0))= epsilon_(r) (Q_(0))/(V_(0))= epsilon_(r)C_(0)` 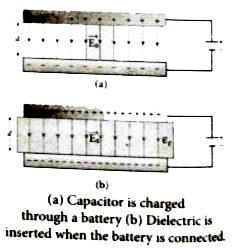 However the reason for the increase in capacitance in this case when the battery remains connected is diferent from the case when the battery is disconnected before introducing the dielectric . Now `C_(0)= (epsilon_(0)A)/(d) ` and `C= (epsilon_(0)A)/(d)` The energy stored in the capacitor before the insertion of a dielectric is given by `U_(0)=(1)/(2)C_(0)V_(0)^(2)` Note that here we have not used the expression `U_(0)=(1)/(2)(Q_(0)^(2))/(C_(0))` because here both charge and capacitance are changed whereas in equation 4 `V_(0)` remains constant . After the dielectric is inserted the capacitance is increased hence the stored energy is also increased . `U =(1)/(2) CV_(0)^(2) = (1)/(2)epsilon_(r)CV_(0)^(2)= epsilon_(r)U_(0)` Since `e_(r) gt 1` we have `U gt U_(0)` It may be noted here that since voltage between the capacitor `V_(0)` is constant the electric field between the plates also remains constant . |
|
| 39463. |
A body of mass 2 kg moving along north east direction with a speed of sqrt 2 m/s . A force of 0.2 N is applied on the body due west for 10 sec. The final velocity of the body is |
|
Answer» `1 m/s `due NORTH |
|
| 39464. |
Two charges of 1.0xx10^(-6) coulombare separated bya distance 10 cm . Where will the electric field be zero on the line joining the two charges ? |
|
Answer» Solution :This is clear that such a point should be some where between the CHARGES because in that case only , electric field will be in opposite direction . Suppose that pointis at a distance x from the charge `q_(1)` , THEREFORE this distance from the charge `q_(2)` will be `(10-x)`. `thereforeE_(1)=(1)/(4piepsilon_(0))(q_(1))/(x^(2))` and `E_(2)=(1)/(4piepsilon_(0))(q_(2))/((r-x)^(2))` But ACCORDING to the problem `E_(1)=E_(2)` `therefore(1)/(4piepsilon_(0))(q_(1))/(x^(2))=(1)/(4piepsilon_(0))(q_(2))/((r-x)^(2))` or , `(1.0xx10^(-6))/(x^(2))=(2.0xx10^(-6))/((10-x)^(2))` or , `(1)/(x)=(sqrt(2))/((10-x))`(Taking positive sign) |
|
| 39465. |
if a charged body is brought near a charged electroscope, then |
|
Answer» The leaves will further diverge the charge on he body is OPPOSITE to that on the eletroscope |
|
| 39466. |
In Young.s double slit experiment 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength 600 nm is used . If the wavelength of light is changed to 400 nm , number of fringes observed in the same segment of the screen is given by |
|
Answer» 18 |
|
| 39467. |
Two wires a and b, each of length 40 m and area of cross-section 10^(-7) m^(2) , are connected in series and a potenital difference of 60 V is applied between the ends of this combined wire. Their resistances are respectively 40 and 20 Omega. Determine for each wire (i) specific resistance, (ii) electric-field and (iii) current-dentsity. |
|
Answer» |
|
| 39468. |
For a metal the maximum wavelength required for photoelectron emission is 340 nm, find the work function. If the radiation of wavelength 250 nm falls on the surface of the given metal. Find the maximum kinetic energy of emitted photo electrons in eV. Given Planck's constant = 6.625 xx 10^(-34) Js, velocity of light in vacuum is 3 xx 10^(8)ms^(-1). |
|
Answer» Solution :`W=(hc)/(lambda_(0))` `W=(6.625 xx 10^(-34) xx 3 xx 10^(8))/(340 xx 10^(-9))` `W=5.84 xx 10^(-34)` or `W=3.65 eV` `E=(hc)/(lambda)` `=(6.625 xx 10^(-34) xx 3 xx 10^(8))/(250 xx 10^(-9))` `=7.95 xx 10^(-19)J` or `E=4.96 eV` `(K.E)_("max")=E-W` `K.E_("max")=2.11 xx 10^(-19)J` or 1.31 eV |
|
| 39469. |
A particle is executing linear simple harmonic motion of amplitude A. At what displacement is the energy of the particle half potential and half kinetic? |
|
Answer» `A/4` KINETIC energy, `K = 1/2 momega^(2) (A^(2)-x^(2))` POTENTIAL energy, `U = 1/2 momega^(2)x^(2)` Total energy,`E = 1/2 momega^(2) A^(2)` As `U = E/2, therefore 1/2 momega^(2) x^(2) =1/2 [1/2 momega^(2) A^(2)]` `x^(2) = A^(2)/2` or `x =A/sqrt(2)` |
|
| 39470. |
A projectile thrown at an- angle of 45^@ to the horizontal has a range 19.6m. Itsvelocity at the highest point is g = 10m/s^2. |
|
Answer» 19.6m/s |
|
| 39471. |
A current l amperes flows through a loop abcdefgha along the edge of a cube of width l metres as shown in figure. One corner 'a' of the loop lies at origin. Now if a uniform external magnetic field is overset-B=B_(0)hatj is switched on, then the unit vector in the direction of torque due to external magnetic field overset(-B) acting on the current carrying loop (abcdefgha) is |
| Answer» Answer :D | |
| 39472. |
A current l amperes flows through a loop abcdefgha along the edge of a cube of width l metres as shown in figure. One corner 'a' of the loop lies at origin. The unit vector in the direction of magnetic field at the centre of cube abcdefgh of width lamda is given by |
|
Answer» `HATI` |
|
| 39473. |
A current l amperes flows through a loop abcdefgha along the edge of a cube of width l metres as shown in figure. One corner 'a' of the loop lies at origin. Thish current path (abcdefgha) can be treated as a superposition of three square loops carrying current l. Choose the correct option? |
|
Answer» fghaf,fabef,ebcde |
|
| 39474. |
Which of the following pairs of physical quantities does not have same units |
|
Answer» IMPULSE and momentum |
|
| 39476. |
A block of mass m slides with constant speed down a ramp whose incline angle is theta. If F_(1) is the magnitude of the gravitational force acting parallel to the ramp and F_(2) is the magnitude of the normal force acting on the block, what is the value of F_(1)//F_(2)? |
|
Answer» m TAN `THETA` |
|
| 39477. |
The speed (v) of ripples on the surface of water depends on surface tension (sigma), density (rho) and wavelength (lambda). The square of speed (v) is proportional to |
|
Answer» `SQRT((GAMMA a)/(RHO))` |
|
| 39478. |
A positive charge q is placed in front of a conducting solid body at a distance d from its center. (a) Find the electric field at the center of the cube due to the charges appearing on its surface. (b) Does the body have to be spherical for the answer to be true ? |
| Answer» Solution :(a) `(Q)/(4pi epsilon_(0)d^(2))`, (b) no | |
| 39479. |
A recatangular loop made of a very thin and flexible wire is kept on a table. The two ends of the wire are connected with two joining screws and a high directe current is allowed to pass through the wire. What will be the shape of the wire and why ? |
Answer» Solution :The rectangular loop is shown in Fig. 1.85. the DIRECTIONS of current in the partsAB and CD are parallel and opposite in directionand hence these two parts repel each other. If the current is too high, the loop will TAKE almost the shape of a circle, that shape is shown by dotted LINE in the figure. 
|
|
| 39480. |
In a p-n junction diode, the depletion region is 400 nm wide and an electric field of 5xx10^(5)V//m exists in it. The minimum kinetic energy of a conduction electron which can diffuse from n side to p side is |
|
Answer» Solution :The p.d ACROSS the junction V = Ed But change in K.E. = work done `therefore` the K.E required to CONDUCT electron from n SIDE to p side = V electron VOLTS `5xx10^(5)xx400xx10^(-9)=0.2eV` |
|
| 39481. |
A wave is described by the equation y = (1.0 mm)sin pi(x/(2.0cm) - 1/(0.01s)) What are the speeds of the particles at x = 1.0 cm at t = 0.012 and 0.013 s? |
| Answer» SOLUTION :18 cm/s, 25 cm/s | |
| 39482. |
What is meant by radio communication ? |
| Answer» Solution :Transmitting and RECEIVING a message in the FORM of a radiowave signal between TWO STATIONS without connecting them with WIRES is known as wireless radio communication. | |
| 39483. |
If the effective value of current on 50 Hz a.c. circuit is 5.0 A. What is (i) peak value of current, (ii) the mean value of current over a half a cycle and (iii) the value of current 1/300 s after it was zero? |
|
Answer» Solution :DATA supplied , `I_m = 5A , V = 50 Hz` i. `i_m = sqrt(2) I_(rms) = sqrt(2) XX 5 = 7.07A` II.`i_m= 2/pi i_m = 0.636 xx 7.07 = 4.5 A` iii.`I = i_m sin 2pi v t = 7.07 xx sin (2pi xx 50 xx 1/300) = 7.07 sin pi/3 = 7.07 x (sqrt3)/(2) = 6.12A` |
|
| 39484. |
Power supplied to a particle of mass 2 kg varies withtime as P =(3t^2)/2W,where t is in seconds. If velocity of particle at t=0 is zero, then the velocity of particle at t=2 s will be |
|
Answer» 1 m `s^(-1)` `therefore K_f-K_i = INT P DT` `rArr 1/2 mv^2-0 = int_0^2 (3/2t^2) dt rArr1/2(2) v^2=3/2 [t^3/3]_0^2 =4` `therefore` Velocity of the particle at t=2 s will be , v=2 m `s^(-1)` |
|
| 39485. |
Arrive at the expressionfor theimpedanceof a seriesLCR circuitusingphasordiagrammethodand hence writethe expressionfor the currentthroughthe circuit . |
|
Answer» Solution :consider a resistance R, an INDUCTOR of self-inductanceL anda capacitor of capacitanceC connectedin seriesacross an AC source. The appliedvoltageis given by , `v=v_0 sin omegat` …(1) 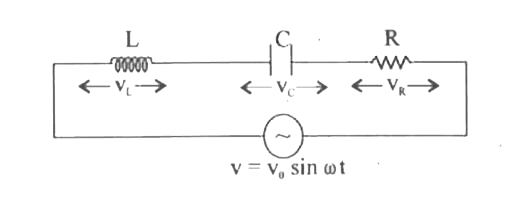 where, v is the instantaneousvalue, `v_0` is the peak VALUE and `omega =2pif` , F being the frequencyof AC. If i be theinstantaneous current at time t, theinstantaneousvotages across R,L and C arerespectivelyiR, `iX_L` and `iX_C`. The vectorsum of the voltageamplitudesacrossR,L , C equalsthe amplitude`v_0`of the voltage applied. Let `V_R, V_L` and `V_C` be the voltageamplitudes acrossR, L and C respectivelyand `I_0` the currentamplitude . Then `V_R=i_0R` is in phasewith `i_0` . `V_L=i_0X_L=i_0(omegaL)` LEADS `i_0` by `90^@` . `v_C=i_0X_C=i_0(1/(omegaC))` lags behind `i_0` by `90^@`. The currentin a pureresistoris PHASE with the voltage, whereas the current in a pure inductorlags thevoltage by `pi/2` rad. The currentin a purecapacitorleads the voltageby `pi/2`rad. For `V_L > V_C` , phaseangle `phi` betweenthe voltageand thecurrentis positive. From theright angled triangle OAP, 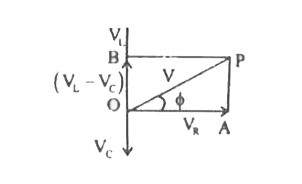 `OP^2=OA^2+AP^2=OA^2+OB^2 ( because AP=OB)` `V^2=V_R^2 +(V_L-V_C)^2 =(iR)^2 +(iX_L-iX_C)^2` `=i^2(R^2 + (X_L-X_C)^2)` `i=V/sqrt(R^2 +(X_L -X_C)^2)=V/Z` and `Z=sqrt(R^2+X_L-X_C)^2` Where Z is the impedanceof the circuit . Phase angle between v & i. tan `phi=(V_L-V_C)/V_R=(X_L-X_C)/R_L` ,`phi=tan^(-1)((X_L-X_C)/R)` |
|
| 39486. |
At a particular instant, a stationary observer on the ground sees a package falling with a speed v_(1) at an angle theta to the vertical. To a pilot flying horizontally with a constant speed v relative to the ground, the package appears to be falling verically with a speed v_(2) (at that same instant). The speed of the pilot relative to the ground (v) is |
|
Answer» `(V_(1)^(2)+v_(2)^(2))^(1//2)` |
|
| 39487. |
In photoelectric effect, the current depends on the |
|
Answer» frequency of LIGHT, but is INDEPENDENT of intensity |
|
| 39488. |
The magnetic flux through a coil is 4xx10^-4Wb/m^2 at time t = 0. It reduces to 10% of its original value in 't' seconds. If the induced e.m.f. is 0.72mV, then what is the time t? |
|
Answer» SOLUTION :`E = (-dphi)/DT = phi_2-phi_1/dt` and `phi_2 = 1phi_1/10` `THEREFORE phi_1-phi_2` = 9phi_1/10` `therefore dt = phi_1-phi_2/e= 9/10xx4xx10^-4//72xx10^-5` = 1/2 = 0.5s |
|
| 39489. |
Helium (He), a monatomic gas, fills a 0.010 m^3 container. The pressure of the gas is (6.2 xx10^5 Pa). How long would a 0.25 hp engine have to run (1 hp = 746 W) to produce an amount of energy equal to the internal energy of this gas? |
|
Answer» `1.0 XX 10^1 s` |
|
| 39490. |
A glass hemisphere of radius R and of material having refractive index 1,5 is silvered on its flat face as shown in Fig. A small object of height h is located at distance 2R from the surface of hemisphere as shown in the figure. The final image will form |
|
Answer» at a DISTANCE of R from silvered surface, on the right side |
|
| 39491. |
A sinusoidal transverse wave of wavelength 18 cm travels along a string in the positive direction of an x axis. The displacement y of the string particle at x= 0) is given in Fig. 16-41 as a function of time t. The scale of the vertical axis is set by y_1= 4.0 cm, The wave equation is to be in the form y(x,t)= y_(nI) sin(kx pm omega t+phi). (a) At t= 0), is a plot of y versus x in the shape of a positive sine function on a legative sinc function? What are (b) y_(nI) (c) k, (d) omega (e) phi, (f) the sign in front of omega, and (g) the speed of the wave? (h) What is the transverse velocity of the particle at x=0 when t=5.0 s? |
Answer» SOLUTION :(a) 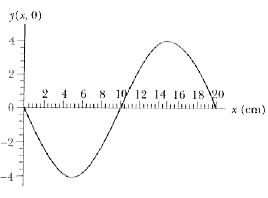 (c) 4.0 cm, (c) 0.35 rad/cm, (d) 0.63 rad/s (e) pi (f) The SIGN is minus since the wave is TRAVELLING in the (H) -2.5cm/s |
|
| 39492. |
The Maxwell’s equation intvecB.vecdl=mu_(0)[I+epsilon_(0).(dphi_(epsilon))/(dt)]is a statement of |
|
Answer» FARADAY’s LAW of induction |
|
| 39493. |
Obtain an expression for effective Capacitance of two Capacitors Connected in series. |
Answer» Solution : ` V = V_1 + V_2` ` V = (Q)/(C_1)` and `V_2 = (Q)/(C_2)` and susbtituting to GET`V = Q =[ (1)/(C_1) +(1)/(C_2)]` ` RARR (1)/(C_5)= (1)/(C_1) + (1)/(C_2)` |
|
| 39494. |
Arjun Dev Charan was........by profession. |
|
Answer» TEACHER |
|
| 39495. |
An object is place 20 cm from a diverging lens. If the distance between the lens and the image is 8 cm, what is the magnification? |
|
Answer» `(1)/(15)` |
|
| 39496. |
For an amplitude modulated wave, the maximum amplitude is found to be 2 V. The modulation index is |
|
Answer» `(2)/(3)` |
|
| 39497. |
At room temperature (27.0^@C)the resistance of a heating element is 100 Omega . What is the temperature of the element if the resistance is found to be 117Omega, given that the temperature coefficientof the material of the resistor is 1.70 xx 10^(-4) ""^@C^(-1) ? |
|
Answer» Solution :Here `T_1 = 27.0^@C , R_1 = 100OMEGA , R_2 = 117 Omega " and " alpha = 1.70 xx 10^(-4) ""^@C^(-1)` `because R_2 =R_1 [1 + alpha (T_2 - T_1) ]` ` therefore 117 = 100 [1+1.7 xx 10^(-4) (T_2 -27) ]` ` RARR T_2 - 27 = (117 - 100)/(100 xx 1.7 xx 10^(-4)) = 1000^@C` `T_2 = 1000+27 = 1027^@C` |
|
| 39498. |
A plane mirror reflecting a ray of incident light is rotated through an angle theta about an axis through the point of incidence in the plane of the mirror perpendicualr to the plane of incidence, then |
|
Answer» The reflected ray does not rotate 
|
|
| 39499. |
Dalton's Atomic theory was not able to explain |
|
Answer» Law of GASEOUS volumes |
|
| 39500. |
Two nuclei have mass number in the ratio 1:64. What is the ratio of their nuclei radii? |
| Answer» SOLUTION :`R_1/R_2=(A_1/A_2)^(1/3)=(1/64)^(1/3)=1:4` | |