Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 40201. |
Two concentric thin metallic spheres of radii R_1 and R_2(R_1 gt R_2) bear charges Q_1and Q_2 respectively. Then the potential at radius r between R_1and R_2 will be (k =1//4 pi in_0) |
|
Answer» `K((Q_1 +Q_2)/(R ) )` |
|
| 40202. |
(a) A particle having a charge of 10 muC and a mass 20 mg is projected with a speed 2 km//sec in a region having a uniform magnetic field of 1 kT. Find the radius of the circle formed by the particle and also time period. (b) A proton, deuteron and alpha-particle enter a region of constant magnetic field perpendicularly. If r_(p), r_(d) and r_(alpha) denote respectively the radii of the trajectories of these particles, then find ratio r_(p):r_(d):r_(alpha) if they enter with same (i) speed, (ii) linear momentum, (iii) kinetic energies. ( c) A charged particle is accelerated through a potential difference V_(0) and acquires a speed of v. It is then injected perpendicular into a magnetic field B. Find the radius of the circle described by it. |
|
Answer» Solution :(a) `q = 10 umC=10^(5)C, m = 20 mg = 20 xx 10^(-6)kg` `v = 2 km//sec = 2 xx 10^(3) m//sec, B = 1 kT = 10^(3)T` `R = (mv)/(Bq) = (20 xx 10^(-6) xx 2 xx 10^(3))/(10^(3) xx 10^(-5)) = 4 m` (b) (i) `r = (mv)/(Bq)`, PROTON `(e, m)`, deutron `(e, 2 m), alpha`-particle `(2e, 4m)` `r_(p):r_(d):r_(alpha) = (mv)/(Be):(2mv)/(Be):(4mv)/(B(2e))` `= 1:2:2` (ii) `r = (p)/(Bq)` `r_(p):r_(d):r_(alpha) = (p)/(Be):(p)/(Be):(p)/(B(2e)) = 1:1:(1)/(2)` `= 2:2:1` (III) `r = (sqrt(2mK))/(Bq)` `r_(p):r_(d):r_(alpha) = (sqrt(2 xx 2mK))/(Be):(sqrt(2 xx 2mK))/(Be):(sqrt(2 xx 4mK))/(B.2e)` `= 1:sqrt(2):1` (c ) When a charged particle of mass `m` having charge `q` is acceleration by a potential `V_(0)`, its kinetic ENERGY `K` is given by `K = qV_(0) = (1)/(2)mv^(2) rArr (q)/(m) = (v^(2))/(2V_(0))` `R = (mv)/(Bq) = (v)/(B).(2V_(0))/(v^(2)) = (2 V_(0))/(Bv)` |
|
| 40203. |
What is the moment of inertia and K.E. of a thin uniform ring of mass 2 kg and diameter 1 m rotating about the axis passing through its centre and perpendicular to the plane of the ring? |
|
Answer» `0.5kgm^(2)` `I=2xx((1)/(2))^(2)=0.5kgm^(2)` |
|
| 40204. |
A nonumiform but spherically symmetric distribution of charge has charge densityprop given as follow - prop =prop_0 (1 - r //R) for prop le R lt brgtprop =0 for r le R whereprop_0 = 3 Q // pi R^3 is a constant ( a) Show that the total charge contained in the charge distrubution is Q. (b)Show that , for the region defined byr le R, the electric field is identical to that produced by a point charge Q. Obtain an expression for the electric field in the regionr le R. (d) Compare your results in part (b) and (c ) r=R. |
|
Answer» `q = INT RHO d v rArr q = int rho_0 ( 1 - r/R ) ( 4 PI r^2 dr ) = rho_0^x` ` 4 pi int_0^R (r^2 - r^3/R) dr` `q =rho_0 4 pi [R^3 /3 - R^4 /(4R) ] = rho 4 pi [R^3 /(12)]` …(1) put `rho _0 = (3Q)/(piR^3)` in EQUATION (1) `q = (3 Q)/(pi R^3) xx ( pi R^3)/3 = Q` (b) From gauss theorem for `r le R` `r le R oint vec E.s vec S = (sumq)/(varepsilon_0) E(4 pi r^2) = (sumq)/(varepsilon_0)` Since `sin q = Q` for `r le R` so `E = 1/( 4 pi in_0) Q/r^2` (C) `E = (sumq)/(4 pi varepsilon_0 r^2)` ...(1) `sum q = int rho d V = int_0^r rho 4 pi r der = rho_0 xx 4 pi int_0^r (r^2-r^3)/(R) dr` ` = (3Q)/(piR^2) xx 4 pi [ r^2 /3 - r^2 /(4R)]` ` q = ( 12Q)/R^2 (r^3 /3 - r^4 /(4R))` ...(2) Sub. (2) in (1) ` E = ( 12 Q)/( 4 pi varepsilon_0r^2 xx R^3) ( r^3 /3 - R^4 /(4 R) ) = (KQr)/R^3 ( 4 - (3r)/R)` (d) In (b) `r =R rArr E = (KQ)/R^2` in ( c) `r = R rArr E = (KQ)/R^2`. |
|
| 40205. |
Huygen.s principle of secondary wavelets can be used to a) deduce the laws of rectraction of light b) deduce the laws of refraction of light c) explain the transverse nature of light waves d) predict the location of a wavefront as time passes |
| Answer» Answer :C | |
| 40207. |
A particle performing uniform circular motion has angular momentum L. If its angular frequency is doubled and its kinetic halved, then the new angular momentum is : |
|
Answer» Solution :Here `E=(1)/(2)Iomega^(2)=(1)/(2)Iomega.omega` `E=(1)/(2)xxL.omega` or `L=(2E)/(omega)orLprop(E)/(omega)` Similarly `L.=(2E.)/(omega.)=(2xx(E)/(2))/(2omega)=(2E.)/(4OMEGA.)=(E)/(2omega)` `therefore (L.)/(L)=((E)/(2omega))/((2E)/(omega))=(1)/(4)` or `L.=(L)/(4)` |
|
| 40208. |
There are two wires of the same material . Their radius and length are in the ratio 1:2 If the extension produced are equal, what is the ratio of the loads |
| Answer» ANSWER :B | |
| 40209. |
An alternating current of rms value 10 A is passed through a 12 Omega resistor. The maximum potential difference across the resistor is |
|
Answer» 20 V The maximum current is `I_(m)=sqrt(2)I_(rms)=sqrt(2)(10)=10sqrt(2)A` Maximum POTENTIAL DIFFERENCE is `V_(m)=I_(m)R` `=10 sqrt(2)xx12 =169.68` V. |
|
| 40210. |
The table gives four sets of values for the circuit elements in Fig 27.33. Rank the sets according to (a) the initial current (as the switch is closed on a) and (b) the time required for the current to decrease to half its initial value, greatest first. |
|
Answer» |
|
| 40211. |
An infinite line charge of uniform charge density lambda is held fixed along the Z-axis of a cartesian cordinate system.A point electric dipole intially kept at the point A (_a, 0 , 0) with the dipolemoment coordinate system. vec(p) along the negative X-direction is moved to the point B(+2a, 0 , 0) and rotated so that its dipolemoment is along the positive X-direction. The work done by the external agent on the dipole in the entire process is |
|
Answer» `-(LAMBDA)/(2PI epsilon_(0)a)` |
|
| 40212. |
The pressure exerted by an emw of intensity 1 (watt//m^2) on a non-reflecting surface is [C is the velocity of light]: |
|
Answer» `IxxC` |
|
| 40213. |
The power is transmitted from a power house on high voltage a.c. because |
|
Answer» electric current travels FASTER at higher volts. |
|
| 40214. |
What will be the path of a charged of a charged particle moving along the direction of uniform magnetic field ? |
| Answer» SOLUTION :As `theta=0, F_m=qvBsintheta=0`. The CHARGED particle moves ALONG it.s original path. | |
| 40215. |
0.6 kg of ice at -10^(@)C is place in a copper calorimeter at 350^(@)C. After some time when thermal equilibrium is attained, calorimeter contains 550 g of ice with some water. Find the water equivalent of the calorimeter. Given that the specific heat of copper is 420 J/kgK, and that of ice 2100J//kg^(@)C and latent heat of ice is 3.32xx10^(-5)J//kg check the answer |
|
Answer» |
|
| 40216. |
A charged hollow sphere does not produce an electric field at any |
|
Answer» inner point |
|
| 40217. |
What amount of heat will be generated in a coil of resistance R due to a charge q passing through it if the current in the coil decreases down to zero uniformly during a time interval t_(0) ? |
|
Answer» `(4)/(3)(q^(2)R)/(t_(0))` |
|
| 40218. |
State the essential conditions which must be satisfied for two light waves to be coherent. |
|
Answer» Solution :They must be of same FREQUENCY the two light waves should be either in PHASE or should have a CONSTANT phase DIFFERENCE. |
|
| 40219. |
A pith ball of mass 9 xx 10^(-5) kg carries a charge of 5muC. What must be charge in another pith ball placed directly 2 cm above the given pith ball such that they held in equilibrium? |
|
Answer» `3.2 xx 10^(-11)C` |
|
| 40220. |
Find the electric field at an arbitrary point of a sphere carrying a charge uniformly distributed over its volume. |
|
Answer» Solution : Let the volume density of the charge `rho=(Q)/(V)=(3Q)/(4pi R^(3))`, where R is the RADIUS of the sphere. Choose a point M Inside the spliere al a distance `r lt R` from its centre and consider a concentric sphere through it. From the results obtained in Problem 24.13 it is evident that the spherical layer lying outside point M does not create a field at this point. The field is created solely by the charge`q=(4)/(3) pi r^(3) rho` CONTAINED inside the smaller sphere. By the result of the previous problem, the field at the SURLACE of this sphere, 1.e. at point M, will be `E=(q)/(4pi epsi_(0)r^(2))=(4pi r^(3) rho)/(3xx 4pi epsi_(0)r^(2))=(rhor)/(3epsi_(0))` We SEE that the field inside the sphere increases in proportion to the radius, at the centre its i tensity is zero, and on the surface it is `E_("sur")=(rhoR)/(3epsi_(0))=(Q)/(4pi epsi_(0)R^(2))` This dependence is plotted in Fig. 24.15. 24.16. The feld potentials on the surfaces of both spheres are `varphi=q//(4pi epsi_(0)R), varphi_(0)=q//(4pi epsi_(0), R_(1))` respectively. The potential difference is `varphi-varphi_(1)=(q)/(4pi epsi_(0))((1)/(R)-(1)/(R_(1)))=(qR(_(1)-R))/(4pi epsi_(0)R R_(1))` The Capacitance is`C=(q)/(varphi-varphi_(1))=(4pi epsi_(0) R R_(1))/(R_(1)-R_(2))` If `d=R_(1)-R lr lt R`, we obtaine the approximation `C=(4pi epsi_(0)R^(2))/(d)=(epsi_(0)S)/(d)` which is the expression for the capacitance of a plane capacitor. The error is `delta=(C_(sp)-C_(pl))/(C_(ap))=(R_(1)-R)/(R)=(d)/(R)` 
|
|
| 40221. |
In the circuit shown in Fig. the capacitor has capacitance C = 20 muF and is initially charged to 100 V with the polarity shown. The resistor R_(0) has resistance 10 Omega. At time t = 0, the switch is closed. The smaller circuit is not connected in any way to teh larger one. the wire of the smaller circuit has a resistance of 1.0 Omega m^(-1) and contains 25 loops. the larger circuit is a rectangle 2.0 m by 4.0 m, while the smaller one has dimensions a = 10.0 cm and b = 20.0 cm. the distance cis 5.0 cm. (The figure is not drawn to scale.) Both circuit are held stationary. Assume that only the wire nearest to teh smaller circuit produces. an appreciable magnetic field through it. The direction of current in the smaller circuit is |
|
Answer» (a) CLOCKWISE `tau = RC = (10 Omega)(20 xx 10^(-6)F) = 200 mus`. Thus, the currnt as a function of time is `I = ((100 V)/(10 Omega))e^((-t)/(200mus))` At `t = 200 ms`, we obtain `I = (10 A)(e^(-1)) = 3.7 A`. Assuming that only the long wire nearest the small loop produces an appreciable magnetic flux through the small loop, `Phi_(B) = int_( c)^(c + a)(mu_(0)ib)/(2pi)dr = (mu_(0)ib)/(2pi)1n(1 + (a)/(c ))` ltbr. So the emf induced in the small loop at `t = 200 ms` `epsilon = -(dPhi)/(dt) = -(mu_(0)ib)/(2pi)1n(1 + (a)/(c ))(DI)/(dt)` `= -(((4pi xx 10^(-7)(Wb))/(A xx m^(2)))(0.200 m))/(2pi) xx 1n (3.0)(-(3.7 A)/(200 xx 10^(-6) s))` Thus, the induced current in the small loop is `i = (epsilon)/(R ) = (0.81 MV)/(25(0.600 m)(1.0 Omega//m)) = 54 muA`. ltbr. Initially current in large loop is maximum and afterwards decreases. Hence flux through the SMALLER loop decreases with time. The induced current willact to oppose the decreases in flux from the large loop. Thus, the induced current flows counterclockwise . |
|
| 40222. |
In the circuit shown in Fig.the capacitor has capacitance C = 20 muF and is initially charged to 100 V with the polarity shown. The resistor R_(0) has resistance 10 Omega. At time t = 0, the switch is closed. The smaller circuit is not connected in any way to teh larger one. the wire of the smaller circuit has a resistance of 1.0 Omega m^(-1) and contains 25 loops. the larger circuit is a rectangle 2.0 m by 4.0 m, while the smaller one has dimensions a = 10.0 cm and b = 20.0 cm. the distance cis 5.0 cm. (The figure is not drawn to scale.) Both circuit are held stationary. Assume that only the wire nearest to teh smaller circuit produces. an appreciable magnetic field through it. The curent in the smaller circuit 200 mus after closing S is |
|
Answer» (a) `54 muA` `TAU = RC = (10 Omega)(20 xx 10^(-6)F) = 200 MUS`. Thus, the currnt as a function of time is `I = ((100 V)/(10 Omega))e^((-t)/(200mus))` At `t = 200 ms`, we obtain `I = (10 A)(e^(-1)) = 3.7 A`. Assuming that only the long WIRE nearest the small loop produces an appreciable magnetic flux through the small loop, `Phi_(B) = int_( c)^(c + a)(mu_(0)ib)/(2pi)dr = (mu_(0)ib)/(2pi)1n(1 + (a)/(c ))` ltbr. So the emf induced in the small loop at `t = 200 ms` `epsilon = -(dPhi)/(dt) = -(mu_(0)ib)/(2pi)1n(1 + (a)/(c ))(di)/(dt)` `= -(((4pi xx 10^(-7)(Wb))/(A xx m^(2)))(0.200 m))/(2pi) xx 1n (3.0)(-(3.7 A)/(200 xx 10^(-6) s))` Thus, the induced current in the small loop is `i = (epsilon)/(R ) = (0.81 mV)/(25(0.600 m)(1.0 Omega//m)) = 54 muA`. ltbr. Initially current in large loop is maximum and afterwards decreases. Hence flux through the smaller loop decreases with time. The induced current willact to oppose the decreases in flux from the large loop. Thus, the induced current flows COUNTERCLOCKWISE . |
|
| 40223. |
In the circuit shown in Fig. the capacitor has capacitance C = 20 muF and is initially charged to 100 V with the polarity shown. The resistor R_(0) has resistance 10 Omega. At time t = 0, the switch is closed. The smaller circuit is not connected in any way to teh larger one. the wire of the smaller circuit has a resistance of 1.0 Omega m^(-1) and contains 25 loops. the larger circuit is a rectangle 2.0 m by 4.0 m, while the smaller one has dimensions a = 10.0 cm and b = 20.0 cm. the distance cis 5.0 cm. (The figure is not drawn to scale.) Both circuit are held stationary. Assume that only the wire nearest to teh smaller circuit produces. an appreciable magnetic field through it. The current in the circuit 200 ms after closing S is |
|
Answer» (a) `(5)/(e) A` `tau = RC = (10 Omega)(20 xx 10^(-6)F) = 200 mus`. Thus, the currnt as a function of time is `I = ((100 V)/(10 Omega))e^((-t)/(200mus))` At `t = 200 ms`, we obtain `I = (10 A)(e^(-1)) = 3.7 A`. Assuming that only the long wire nearest the small loop produces an appreciable MAGNETIC flux through the small loop, `Phi_(B) = int_( c)^(c + a)(mu_(0)ib)/(2pi)dr = (mu_(0)ib)/(2pi)1n(1 + (a)/(c ))` ltbr. So the emf induced in the small loop at `t = 200 ms` `epsilon = -(dPhi)/(dt) = -(mu_(0)ib)/(2pi)1n(1 + (a)/(c ))(di)/(dt)` `= -(((4pi xx 10^(-7)(Wb))/(A xx m^(2)))(0.200 m))/(2pi) xx 1n (3.0)(-(3.7 A)/(200 xx 10^(-6) s))` Thus, the induced current in the small loop is `i = (epsilon)/(R ) = (0.81 mV)/(25(0.600 m)(1.0 Omega//m)) = 54 muA`. ltbr. Initially current in large loop is maximum and afterwards decreases. Hence flux through the smaller loop decreases with time. The induced current willact to oppose the decreases in flux from the large loop. Thus, the induced current FLOWS counterclockwise . |
|
| 40224. |
Give the expression for the impedance of an LCR circuit and obtain the expression for the resonant frequency. What is the power factor of the resonant circuit? |
|
Answer» Solution :Impedance of a series LCR circuit is given by `Z=sqrt(R^(2)+(X_(L)-X_(C))^(2))=sqrt(R^(2)+(omegaL-(1)/(omegaC))^(2))` Where, `omega=2pif`, f being frequency of ac. i.e., `omega_(0)^(2)LC=1` `therefore omega_(0)=(1)/(sqrt(LC))or2pif_(0)=(1)/(sqrt(LC))` `therefore f_(0)=(1)/(2pisqrt(LC))`, where `f_(0)` is known as the resonant frequency. Power FACTOR = cos R/Z and Z = R at resonant frequency. Power factor = cos R/R = 1. VOLTAGE is in PHASE with CURRENT. |
|
| 40225. |
Name the material used for making standard resistance. Give reasons. |
| Answer» Solution :The alloys such as MANGANIN, CONSTANTAN or nichrome are USED for making standard resistance. For the reasons that they possess high resistivity and low TEMPERATURE co.efficient of resistance. | |
| 40226. |
As the mass number A increases, which of the following quantities related to a nucleus do not change ? |
|
Answer» BINDING energy |
|
| 40227. |
The magnifying glass is made of combination of lenses of power +20 D and -4D. If the distance of distinct vision is 25 cm, calculate the size of an object 2 cm high seen through the magnifying glass. |
|
Answer» |
|
| 40228. |
An ideal solenoid having 40 turns/cm has an aluminium core and carries a current of 2.0 A. Calculate the magnetization l developed in the core and the magnetic field B at the centre. The susceptibility X of aluminimum = 2.3 xx 10^(-5). |
|
Answer» SOLUTION :The magnetic intensity H at the centre of the solenoid is H = ni = 4000 turns/m `xx 2.0 A= 8000 A//m` the MAGNETIZATION is `I=etaH` `=2.3xx10^(-5)xx8000A//m=0.18A//m` The magnetic field is `B=mu_(0)(H+I)` `=(4pixx10^(-7)T-m//A)[800+0.18]A//m=3.2pixx10^(-4)T` Note that H >>I in case of a paramagnetic core |
|
| 40229. |
(a) Define the current sensitivity of a galvonometer . (b) The coil area of a galvonometer is 16 xx 10^(-4) m^(2). It consists of 200 turns of wire and is in a magnetic field of 0.2 T. The restoring torque constant of the suspended fibre is 10^(-6) N m per degree . Assuming the magnetic field to be radial, calculate the maximum current that can be measured by the galvanometer if the scale can acomodate 30^@ deflection. |
|
Answer» SOLUTION :(b) Here area `A = 16 xx 10^(-4) m^(2)`, no. of turns `N = 200`, magnetic field B = 0.2 T, torque constant `k = 10^(-6) N - m` PER DEGREE and maximum DEFLECTION `phi = 30^@`. Hence, maximum current that can be `I = k/(N A B) phi= (10^(-6) xx 30)/(200 xx (16 xx 10^(-4)) xx 0.2) = 4.7 xx 10^(-4) "or" 0.47 mA`. |
|
| 40230. |
A receiver and a source of sonic oscillations of frequency v_(0)=2000Hz are located on the x axid. The source swings harmonically along that axis with a circulat frequency bandwidth registered by the stationary receiver be equal to Delta v=200 Hz ? The velocity of sound is equal to v=340 m//s. |
|
Answer» Solution :Obviosuly the maximum FREQUENCY will be HEARD when the source is moving with maximum velocity towards the receiver and minimum frequency will be ehard when the source recedes with maximum velocity. As the source swing harmonically its maximum velocity equals `a OMEGA`. Hence `v_(max)=v_(0)(v)/( v- a omega)` and `v_(min )=v_(0)(v)/(v+a omega)` So the frequency band width `DELTA v = v_(max) - v _(min)= v_(0) v ((2 a omega)/( v^(2)-a^(2) omega^(2)))` or, `(Deltava^(2))omega^(2)+(2 v_(0)v a ) omega - Delta v v ^(2) = 0 ` so, `omega=(-2 v_(0)v a +- sqrt(4 v _(0)^(2) v ^(2) a ^(2) + Delta v^(2) a ^(2) v^(2)))/( 2 Delta v a ^(2))` On simplifying ( and taking `+` SIGN as `omega rarr0` if `Delta v rarr0)` `omega = ( v v_(0))/( Deltava)(sqrt(1+ ((Deltav)/( v_(0)))^(2))-1)` |
|
| 40231. |
What is attenuation in communication system ? |
| Answer» Solution :It REFERS to LOSS of STRENGTH of a signal during propagation of a signal. | |
| 40232. |
The circuit is in a steady state. The charge in capacitor C_3 is |
|
Answer» `10 muC` 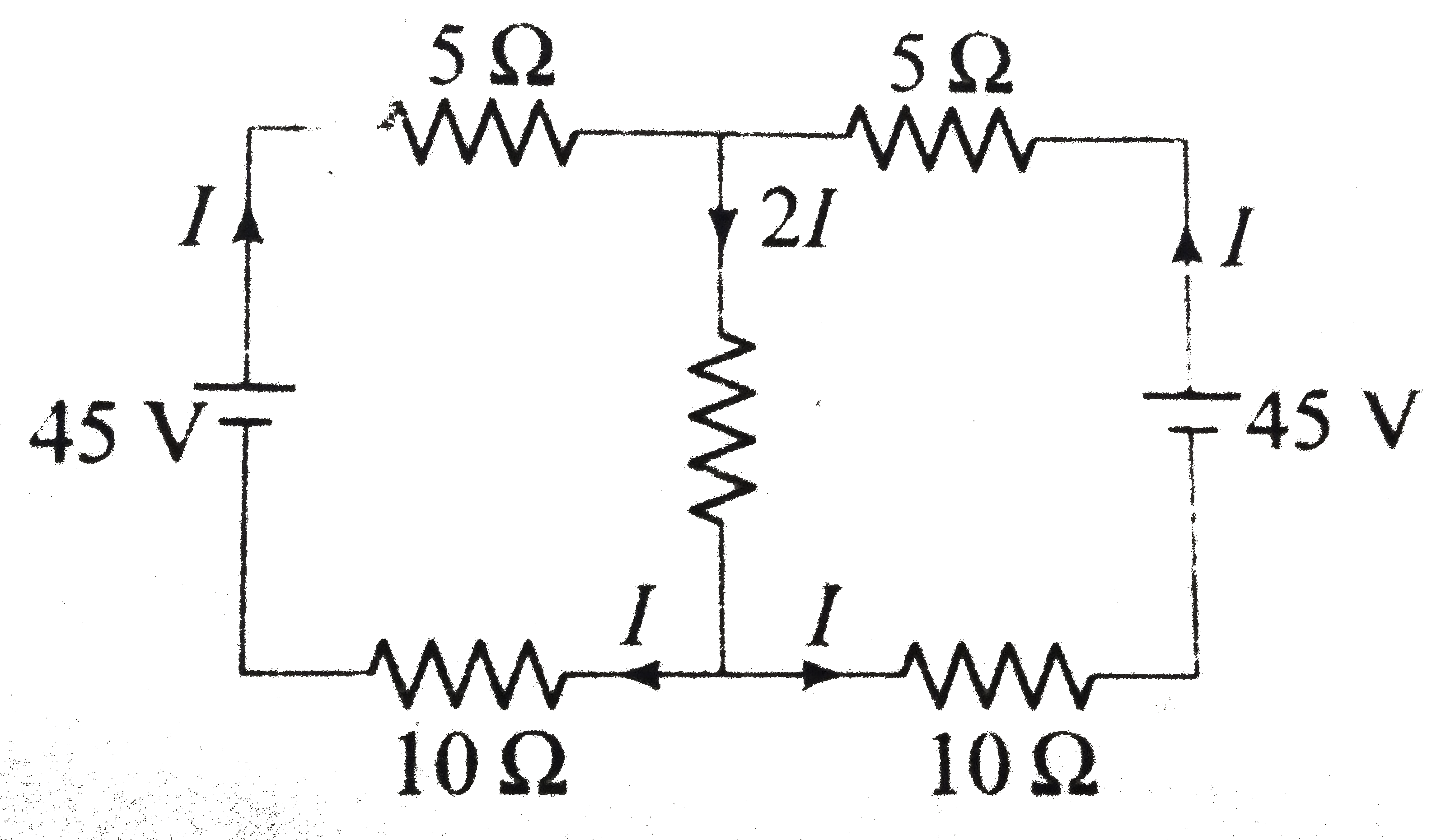 Using Kirchhoff's law, we can calculate `I = 1A` . Further using Kirchhoff's law in original circuit, we can calculate charges on different CAPACITORS. |
|
| 40233. |
An n-p-n transistor is connected in common - emitter configuration as shown in V_(BE)=0.6V,V_(CE)=3 and common - emitter current amplification factor is 50, then the values of R_(1) and R_(2) are respectively. |
|
Answer» `1 K OMEGA, 74 kg Omega` `rArr"" R_(B)=R_(1)=(V_("CC")-V_("BE"))/(i_B)` As,`i_(B)= (i_c)/(Beta)= (5 XX 10^(-3))/(50)=1 xx 10^(-4)A` `rArrR_(1)= (8-0.6)/(1 xx 10-4) = 7.4 xx 10^4 = 74 xx 10^3 Omega=74 k Omega` and by KVL in closed collector loop, we get `V_("CC")=i_(C)R_(L)+V_(CE)` `rArr "" R_(L)= V_("CC"-V_("CE"))/(i_C)` `= (8-3)/(5 xx 10^(-3))` So,`R_(2)= R_(L)=1.0 k Omega` |
|
| 40234. |
The distortion in the transmission and processing of signals is called |
|
Answer» INTERFERENCE |
|
| 40235. |
A bulb of 220V and 300 W is connected across 110v circuit .The percentage reducation in it's power is : |
| Answer» ANSWER :D | |
| 40236. |
What type of phenomenon can be used as a measure of time ? Give two examples. |
| Answer» Solution :Any phenomenon that happens regularly with TIME can be made use of as a STANDARD of time Examples are periodic vibration of pendulum, oscillation of CERTAIN crystals, DECAY of radioactive substance etc. | |
| 40237. |
Consider an arbitrary electrostatic field configuration. A small test total is placed at a null point (i.e,whereoversetto E=0)of the configuration. Show that the equilibriumof the testchargeis necessarilyunstable. (b)Verify this result for the simpleconfiguration of two charges of the same magnitudeand sign placed a certaindistance apart. |
|
Answer» Solution :Let uspresume that the equilibriumof the test chargesat the NULL-pointis stable .Then the testchargesdisplacedslightly in anydirectionmustexperience a restoringforcetowards the null-point.It meansthat all field lines NEAR the null-point should be directedinwardstowardsthe null-pointHowever , by Gauss.s lawthe electricfluxthrough a surfacenot enclosing any CHARGES, mustbe zero -Henceor presumption is wrongor itmeans that the equilibriumof thetest charge at the null-pointis necessaryunstable. (b)We know that if two charges of same magnitude and sign are placed a certaindistance apart, the mid-pointof the line joining two charges is a ull-point.Displace the testcharges placed at NEUTRAL point slightlyin a normal direction. Wefind that the a net forceacts now on the test charges and takes it away from the neutral point i.e., testchargesdoes not returnto the null- point . It showsthat the equilibriumis a UNSTABLE equilibrium. |
|
| 40238. |
When polaroid is rotated intensity of light increases and decreases but never becomes zero, so we can say that incident light is ....... |
|
Answer» completely plane polarised |
|
| 40239. |
A source of sound and an observer are approaching each other with the same speed, which is equal to 1/10 times the speed of sound. The apparent relative change in frequency of source is: |
|
Answer» 22.2% INCREASES |
|
| 40240. |
When there is resonance in an a.c. circuit containing L,C,R the circuit: |
|
Answer» is zero |
|
| 40241. |
The dimensions of 'resistance' are same as those of. . . . . . . . .Where h is the Planck's constant e is the charge . |
|
Answer» `(h)/(E^(2))` Dim. Of `(h)/(e^(2))=(ML^(2)T^(-1))/(A^(2)T^(2))=[ML^(2)T^(-3)A^(-2)]` So CORRECT choice is `(a). |
|
| 40242. |
How does the angular separation between fringes in single-slit diffraction experiment change when the distance of separation between the slit and screen is doubled ? |
| Answer» SOLUTION :No CHANGE. | |
| 40243. |
A copper wire of length 50.0 cm and total resistance of 1.1 xx 10^(-2) Omegais formed into a circular loop and placed perpendicular to a uniform magnetic field that is increasing at the constant rate of 10.0 mT/s. At what rate is thermal energy generated in the loop? |
|
Answer» `1.32 xx 10^(-8) W` `R = 1.1 xx 10^(-2) Omega ` `(DB)/(DT) = 10.0 mT//s= 10 xx 10^(-3) T//s` Let r the radius of a circular loop `therefore2pir = I. r = (L)/(2pi) = (50 xx 10^(-2))/(2pi) m = (1)/(4PI) m` Magnetic flux linked with the loop is `phi= BA cos theta = Bpi r^2 cos 0^@= Bpi r^2` Emf induced in the loop is `|epsi| = (dphi)/(dt) = pi r^2(dB)/(dt)` Rate at which thermal energy generated in the loop is `P = (|epsi|^2)/( R) = ((pi r^2)^2 ((dB)/(dt))^2)/( R)` Substituting the GIVEN values ,we GET `P = (pi^2 xx ((1)/(4pi))^4 xx (10 xx 10^(-3))^2)/(1.1 xx 10^(-2) ) = 3.62 xx 10^(-6) W` |
|
| 40244. |
Consider the following statements (A) The refractive index of the extraordinary ray depends on the angle of incidence in double refraction (B) The vibractions of light waves acquire one -sideness for both ordinary and extraordinary rays in double refraction (C ) Diffraction fringes will be always unequally spaced . |
|
Answer» A and B , are TRUE |
|
| 40245. |
Photo electric effect supports quantum nature of light because |
|
Answer» There is a minimum FREQUENCY below which no photo electrons are emitted |
|
| 40246. |
The horizontal range of an oblique projectile is equal to the distance through which a projectile has to fall freely from rest to acquire a velocity equal to the velocity of projection in magnitude. The angle of projection is |
| Answer» ANSWER :A | |
| 40247. |
A small bar magnet has a dipole moment 1.2 A m^2. The magnitude of magnetic field at a distance of 0.1 m on its axis will be |
|
Answer» `1.2xx10^(-4)T` |
|
| 40248. |
(a) Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of 500 V with respect to the emitter. Ignore the small initial speeds of the electrons. The specific charge of the electron, i.e., its e/m is given to be 1.76 xx 10^(11) C kg^(-1) . (b) Use the same formula you employ in (a) to obtain electron speed for an collector potential of 10 MV. Do you see what is wrong ? In what way is the formula to be modified? |
|
Answer» Solution :(a) Use `eV=(MV^(2)//2)" i.e., "V=[(2eV//m)]^(1//2),v=1.33xx10^(7)ms^(-1)` (b) If we use the same formula with `V = 10^(7) V`, we get `v = 1.88 × 10^(9) m s^(-1)`. This is clearly wrong, since nothing can move with a speed greater than the speed of light `(c = 3 xx10^(8) m s^(-1))`. Actually, the above formula for kinetic energy `(m v^(2)//2)` is valid only when `(v//c) lt lt 1`. At very high speeds when (v/c ) is comparable to (though always less than) 1, we come to the relativistic domain where the following formulae are valid: Relativistic momentum `p = m v` Total energy `E = m c^(2)` Kinetic energy `K = m c^(2) - m_(0) c^(2)` , where the relativistic mass m is given by `m=m_(0)(1-(v^(2))/(c^(2)))^(-1//2)` `m_(0)`is called the rest mass of the particle. These relations also imply: `E=(p^(2)c^(2)+m_(0)^(2)c^(4))^(1//2)` Note that in the relativisitc domain when v/c is comparable to 1, K or energy `ge m_(0)c^(2)` (rest mass energy). The rest mass energy of ELECTRON is about 0.51 Mev. Thus a kinetic energy of 10 Mev, being MUCH greater than electron’s rest mass energy, implies relativistic domain. Using relativistic formulas, v (for 10 Mev kinetic energy) `= 0.999 c`. |
|
| 40249. |
A body of height 1m stands in front of a convex mirro. His distance from the mirror is equal to its focal length. The height of his image is |
|
Answer» `0.25m` |
|
| 40250. |
(a) Using Bohr's second postulate of quantization of orbital angular momentum, show that the circumference of the electron in the nth orbital state in hydrogen atom is n times the de-Broglie wavelength associated with it. (b) The electron in hydrogen atom is initially in the third excited state. What is the maximum number of spectral lines which can be emitted when it finally moves to the ground state ? |
|
Answer» <P> SOLUTION :According to Bohr.s second postulate`mvr_(n)=(nh)/(2pi)` `rArr 2pir_(n)=(nh)/(mv)` But `(H)/(mv)=(h)/(p)= lambda` But `(h)/(mv)=(h)/(p)=lambda` `:. 2pi r_(n)=n lambda` (b) For third excited state, `n=4` for ground state `n=1` Hence possible transitions are `n_(f)=4 "to" n_(i)=3,2,1` `n_(f)=3 "to" n_(i)=2,1` `n_(f)=2"to" n_(i)=1` otal NUMBER of transitions = 6 |
|