Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 40701. |
A particle, which is constrained to move along the x-axis, is subjected to a force in the same direction which varies with the distance of the particle from the origin as F(x)=-kx+ax^(3). Hence k and a are positive constants. For 20. the functional form of the potential energy U(x) of the particle is: |
|
Answer»
Also, we know that `F(x)=-(dU)/(dx)` `:.P.E., U=-intF.dx` =`-INT(-kx+ax^3)dx` `U=(kx^2)/(2)-(ax^4)/(4)` This follows that U=0 at two valves of x i.e. `(kx^2)/(2)-(ax^4)/(4)=0` `(x^2)/(2)[k-(ax^2)/(2)]=0` `:.` x=0 and`x=sqrt((2k)/(a))`. This means the graphs (b) and (C) are not possible. Further U is maximum or minimum, when `(dU)/(dx)=0`. i.e. `-(-kx+ax^3)=0` `kx-ax^3=0` `x(k-ax^2)=0` `:.` EITHER x=0 or `x=sqrt(k/a)`. For the value of `sqrt(k/a)=x`, U will be max., Where `(d^2U)/(dx^2)lt0` Now `(d^2U)/(dx^2)=(d)/(dx)(kx-ax^3)=k-3ax^2` =`k-3a(sqrt(k/a))^2=-2k` THUS, U is max. at `x=sqrt(k/a)` and minimum NEGATIVE for `xgtsqrt((2k)/(a))`.Hence graph (a) is also ruled out. |
|
| 40702. |
The vertical plane dip circle is perpendicular to the magnetic meridian.The dip needle reads |
|
Answer» 0-0 |
|
| 40703. |
Two rods having the same proper length l_0 move lengthwise toward each other parallel to a common axis with the same velocity v relative to the laboratory frame of reference. What is the length of each rod in the reference frame fixed to the other rod? |
|
Answer» Solution :The VELOCITY of one of the rods in the reference FRAME FIXED to the other ROD is `V=(v+v)/(1+v^2/c^2)=(2V)/(1+beta^2)` The length of the moving rod in this frame is `l=l_0sqrt(1-(4v^2//c^2)/((1+beta^2)^2))=l_0(1-beta^2)/(1+beta^2)` |
|
| 40704. |
A) It is possible to have mutual inductance with out self-inductance B) If the current in an inductor is doubled, the stored energy in it is quadrupled C) One can have an inductance without a resistance |
|
Answer» A & B are false |
|
| 40705. |
In a transformer no. of turns in a primary is 140 and that in the secondary is 280. If current in the primary is 4A then the current in the secondary is, |
|
Answer» 2A |
|
| 40706. |
When an ideal capacitor is charged by a d.c. battery, no current flows. However, when an a.c. source is used, the current flows continuously. How does one explain this, based on the concept of displacement current ? |
|
Answer» Solution :When an ideal capacitor is fully CHARGED by a d.c. battery, the electric field `vecE` between the plates of capacitor does not CHANGE with TIME. Therefore, displacement current is ZERO. When an a.c. source is applied between the plates of an ideal capacitor, the electric charge on plates and consequently electric field `vecE` between the plates of capacitor is CONTINUOUSLY changing with time. Consequently a displacement current is set up and we say that a current is flowing through the capacitor. |
|
| 40707. |
Statement (A): Alkali metals exhibit photo electric effect when they illuminated with visible light. Statement (B): Photoelectric emission is also like thermionic emission. |
|
Answer» A is TRUE, B is FALSE |
|
| 40709. |
Radioactive ""_(27)^(60)Co is transformed into stable ""_28^60Ni by emitting two gamma - rays of energies |
|
Answer» A) `1.33 MEV and 1.17 MeV` is succession |
|
| 40710. |
Is it possible that a nucleus has negative mass defect? |
| Answer» Solution :No, negative mass defect is not possible. This would MEAN creation of mass as well as BINDING ENERGY which would violate the PRINCIPAL of energy CONSERVATION. | |
| 40711. |
A thick rope of rubber of density 1.5 kg//m^(3) and Y = 5 xx 10^(6) Nm^(-2) 8 metres in length when hung vertically will increase in length by : (g = 10 ms^(-2)) |
|
Answer» `9.6 xx 10^(-5)` m `therefore` Only HALF the length ofrope gets extended. `Y=F/A.((L//2))/(Deltal)` `thereforeDeltal=(Mg)/(AY).L/2=(ALpg.h)/(2Ay)=(L^(2)pg)/(2Y)` `=(64xx1.5xx10)/(2xx5xx10^(6))=9.6xx10^(-5)m` So, the CORRECT choice is (a). |
|
| 40712. |
A body of uniform cross-sectional area floats in a liquid of density thrice its value. The portion of exposed height will be : |
| Answer» Answer :A | |
| 40713. |
Y (x,t) = (0.8)/([(4x + 5t)^2 + 5])represents a moving pulse where x and y are in metre and t is in second. Then |
|
Answer» PULSE is moving in POSITIVE x-direction |
|
| 40714. |
A fraction f_1 of a radioactive sample decays in one mean life, and a fraction f_2 decays in one half life. Then |
|
Answer» `f_1 gt f_2` and half life , `T_(1//2)="In2"/lambda=0.693/lambda` `therefore tau gt T_(1//2)`. GREATER fraction will decay in longer time. Hence, fraction DECAYED in one mean life MUST be greater than the fraction decayed in one half life i.e. `f_1 gt f_2`. |
|
| 40715. |
Here are examples of how to use Newton's second law for a quck when one or two forces act on it. Parts (a), (b), and ( c ) of Fig. 5-3 show three situations in which one or two forces act on a puck that moves over frictionless ice along an x axis, in one-dimensional motion. The puck's mass is m = 0.20 kg. Forces vec(F)_(1) and vec(F)_(2) are directed along the axis and have magnitudes F_(1)=4.0 N and F_(2)=2.0 N. Force vec(F)_(3) is directed at angle theta=30^(@) and has magnitude F_(3)=1.0 N. In each situation, what is the acceleration of the puck ? |
|
Answer» Solution :In each situation we can relate the ACCELERATION `vec(a)` to the net force `vec(F)_("net")` acting on the puck with Newton.s second law, `vec(F)_("net")=m vec(a)`. However, because the motion is along only the x axis, we can simplify each situation by writing the second law for x components only: `F_("net.x")=ma_(x).""(5-4)` The free-body diagrams for the three situations are also given in FIG. 5-3, with thee puck represented by a dot. Calculations : Situation A: Foor Fig. 5-3b, where only one horizontal force acts, Eq. 5-4 gives us `F_(1)=ma_(x)`, which, with given data, yields `a_(x)=(F_(1))/(m)=(4.0N)/(0.20kg)=20" m"//"s"^(2)`. The positive answer indicates that the acceleration is in the positive direction of the x axis. Situation B: In Fig. 5-3d, two horizontal forces act on the puck, `vec(F)_(1)` in the positive direction of x and `vec(F)_(2)` in the NEGATIVE direction. Now Eq. 5-4 gives us `F_(1)-F_(2)=ma_(x)`, which, with given data, yields `a_(x)=(F_(1)-F_(2))/(m)=(4.0N-2.0N)/(0.20kg)=10" m"//"s"^(2)`. Thus, the net force accelerates the puck in the positive direction of the x axis. Situation C: In Fig. 5-3f, force `vec(F)_(3)` is not directed along the direction oof the puck.s acceleration, only x component `F_(3,x)` is. (Force `vec(F)_(3)` is two-dimensional but the motion is only one-dimensional.) Thus, we write Eq. 5-4 as 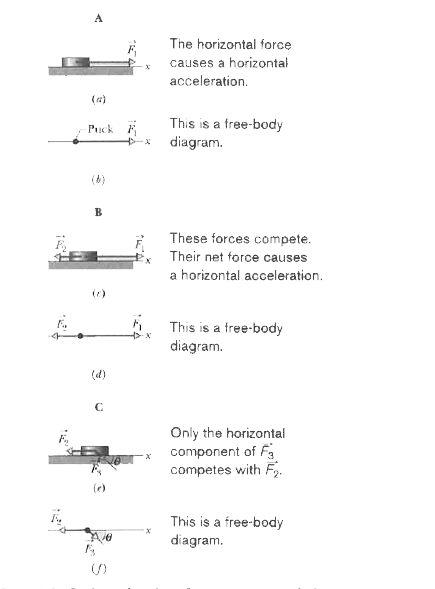 FIGURE 5-3In three situations, forces act on a puck that moves along an x axis. Free-body diagrams are also shown. `F_(3,x)-F_(2)=ma_(x).""(5-5)` From the figure, we see that `F_(3,x)=F_(3)cos theta`. Solving for the acceleration and substituting for `F_(3,x)` yield `a_(x)=(F_(3,x)-F_(2))/(m)=(F_(3)cos theta-F_(2))/(m)` `=((1.0N)(cos 30^(@))-2.0N)/(0.20kg)=-5.7" m"//"s"^(2).` Thus, the net force accelerates the puck in the negative direction of the x axis. |
|
| 40716. |
What is the minimum number of vectors to give zero resultant. |
|
Answer» 3 |
|
| 40717. |
Two positive charges of magnitude q are placed at the ends of a side (side 1 )of square of side 2a. Twonegative cahrges of the same magnitude ar kept at the other comers. Starting from rest, if the charge Q moves from the middle of side (1)to thecentre of square , its kinetc energy at the centre of square is |
|
Answer» `1/(4 PI in_(0)) (2qQ)/a (1 - 1/(sqrt(5))) ` AC = AD = a ` AE = AF = sqrt(a^(2)+ (2a)^(2))` `= sqrt(5) a ` `BC = BD= BE= BF = sqrt2 a` Potential at pointA is ` V_(A)( 1/(4 pi in_(0)) q/(AC)+ 1/(4 pi in_(0)) q/(AD) -1/(4 pi in_(0)) q/(AE) - 1/(4 pi in_(0)) q/(AF))` `= 1/(4 pi in_(0) q/a + 1/( 4 pi in_(0)) q/a - 1/(4 pi in_(0)) q/(sqrt(5a)) - 1/(4 pi in_(0)) q/(sqrt(5a)))` `V_(A) = 2 (1/(4 pi in_(0) q/a)) -2 1/(4 pi in_(0)) q/(sqrt(5a)) = 1/(4 pi in_(0)) (2q)/a ( 1- 1/sqrt(5))` Potenital at pointB is ` V_(B)( 1/(4 pi in_(0)) q/(BD)+ 1/(4 pi in_(0)) q/(BE) -1/(4 pi in_(0)) q/(AE) - 1/(4 pi in_(0)) q/(BF))` ` (1/(4 pi in_(0))q/sqrt(2a) + 1/(4 pi in_(0)) q/(sqrt2a)- 1/(4 pi in_(0)) q/(sqrt(2 a)) - 1/(4 pi in_(0)) q/(sqrt(2a))` `V_(B)= 2 1/( 4 pi in_(0) q/(sqrt(2)a))- 2 (1/(4 pi in_(0))q/(sqrt(2)a) = 0` ` thereforeV_(A)-V_(B)= 1/(4 pi in_(0) (2q)/a (1-1/sqrt5)` Kineticenergyat the centre of squareof charge Q = WORK done on CHARGEQ fromA to B is ` W = Q (V_(A)-B-V_(B)) = 1/( 4pi in_(0)) ( 2 qQ)/a ( 1- 1/sqrt(5))` 
|
|
| 40718. |
What is the outcome of Davission Germer Experiment? |
| Answer» Solution :Davisson GERMER EXPERIMENT CONFIRMS that electrons in motion BEHAVE as a WAVE. | |
| 40719. |
The work function of a metallic surface in 5.0/eV. Photoelectrons are emitted when light of lamda=2000Å falls-on it. The P.D. to stop fastest photoelectrons is : |
|
Answer» 1.2 V `-1.2 V` on SOLVING |
|
| 40721. |
source emitting a sound of frequency V is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v. |
|
Answer» `(V v^2)/(2Vv - a)` |
|
| 40723. |
What must be the relative velocity of a source and an aboserber consisting of freeIr^(191) nuclei to observe the maximum absorption of gamma quanta with energy epsilon=129keV? |
Answer» Solution :For maximum (resonant) absorption, the absorbing nucleus MUST be MOVING with enough SPEED to cancel the momentum of the oncoming photon and have just right enrgy `(epsilon= 129keV)` availiable for transition to excited STATE  Since `deltaE_(gamma)OVERSET~-(epsilon^(2))/(2Mc^(2))` and momentum of the photon is `(epsilon)/(c )`, these condition can be satisfied if the velocity of the nucleus is `(epsilon)/(Mc)=c(epsilon)/(Mc^(2))= 218m//s= 0.218 km//s` |
|
| 40724. |
A magnt of magnetic dipole moment M is released in a uniform magnetic field of induction B from the position shown in the figure. Find : will it perform SHM? oscillation ? Periodic motion ? What is its amplitude ? |
|
Answer» SOLUTION :SINCE `'theta'` is not small. `therefore`the MOTION is not S.H.M. but it is oscillatory and periodic AMPLITUDE is `120°`. |
|
| 40725. |
What is absolute refractive Index ? |
| Answer» SOLUTION :The absolute RI of a medium is DEFINED as `mu`=C/v. where C= Velocity of LIGHT through vaccem.and v = velocity of light through medium. | |
| 40726. |
A sample of 100 millicurie of krypton gas consists of a mixture of the active isotope .^(85)Kr & the stable isotope .^(84)Kr. If the volume of the mixtures 10 cm^(3) at STP & half-life of .^(85)Kr is 10 years. Calculate the % by weight of .^(85)Kr present in the mixture. |
|
Answer» |
|
| 40727. |
An isolated conducting sphere of radius 6cm has a charge of 1.5 muC. Calculate the energy stored in the field of this charged conductor and the energy density at the surface of the sphere. |
|
Answer» |
|
| 40728. |
A magnt of magnetic dipole moment M is released in a uniform magnetic field of induction B from the position shown in the figure. Find : its maximum kinetic energy during the motion. |
|
Answer» Solution : K.E. will be maximum where P.E. is MINIMUM. P.E. is minimum at `theta=0^(@)`. Now apply energy conservation between `theta=120^(@)andtheta=0^(@)`. `-mBcos120^(@)+0` `=-mBcos0^(@)+(KE)_(max)` `(KE)_(max)=(3)/(2)MB`. The K.E. is max at `theta = 0°` can also be proved by TORQUE METHOD. From `theta = 120°` to `theta = 0°` the torque always acts on the dipole in the same direction (here it is clockwise) so its K.E. keeps on increases till `theta=0°`. Beyond that reverses its direction and then K.E. starts decreasing `THEREFORE theta=0^(@)`is the orientation of M to here the maximum K.E. |
|
| 40729. |
A stream of electrons accelerated by a potential difference V falls on the surface of a metal whose inner potential is V_(i)= 15V. Find: (a) the refractive index of the metal for the electrons accelerated by a potential difference V= 150V, (b) the values of the raito V//V_(i) at which the refracticve index differs from unity by not more than eta=1.0%. |
|
Answer» Solution :Inside the metal, there is a negative potential energy of `-eV_(i)`. (This potential energy prevents electron from leaking out and can be measured in photoelectric EFFECT ets.)An electron whose `K.E` is `eV` outside the metal will FIND its `K.E` increased to `e(V+V_(i))` in the metal. Then (a) de Broglie wavelength in the metal `=lambda_(m)=(2piħ)/(sqrt(2m e (V+V_(i))))` Also DEBROGLIE wavelength in Vacuum `=lambda_(0)=(2PI ħ)/(sqrt(2 mVe))` Hence refractive index `n=(lambda_(0))/(lambda_(m))=sqrt(1+(V_(i))/(V))` Substituting we get `n=sqrt(1+(1)/(10))~=1.05` (b) `n-1= sqrt(1+(V_(i))/(V))-1leeta` then `1+(V_(i))/(V)LE(1+eta)^(2)` or `V_(i)leeta(2+eta)V` or `(V)/(V_(i))ge(1)/(eta(2+eta))` For `eta= 1% = 0.01` we get `(V)/(V_(i))ge50` |
|
| 40730. |
A magnt of magnetic dipole moment M is released in a uniform magnetic field of induction B from the position shown in the figure. Find : Its kinetic energy at theta=90^(@) |
|
Answer» Solution :Apply ENERGY CONSERVATION at `theta=120^(@)andtheta=90^(@)` `-MBcos120^(@)+0` `=-MBcos90^(@)+(K.E)` `KE=(MB)/(2)` |
|
| 40731. |
The work function of caesium is 2.14 ev. Find (a) the threshold frequency for caesium, and (b) the wavelength of the incident light if the photocurrent is brought to zero by a stopping potential of 0.60 V. |
|
Answer» Solution :For the cut-off or threshold frequency, the energy h `ν_(0)` of the incident radiation must be equal to work FUNCTION `phi_(0)`, so that `v_(0)=(phi_(0))/(h)=(2.14ev)/(6.63xx10^(-34)Js)` `=(2.14xx1.6xx10^(-19)J)/(6.63xx10^(-3)Js)=5.16xx10^(14)Hz` Thus, for frequencies less than this threshold frequency, no photoelectrons are ejected. (b) Photocurrent reduces to zero, when MAXIMUM kinetic energy of the emitted photoelectrons EQUALS the potential energy `e V_(0)` by the retarding potential `V_(0)` . EINSTEIN’s Photoelectric equation is `eV_(0)=hv-phi_(0)=(hc)/(lambda)-phi_(0)` `or, lambda=hc//(eV_(0)+phi_(0))` `=((6.63xx10^(-34)Js)xx(3xx10^(8)m//s))/((0.60ev+2.14eV))` `=(19.89xx10^(-26)JM)/((2.74eV))` `lambda=(19.89xx10^(-26)Jm)/(2.74xx1.6xx10^(-19)J)=454nm` |
|
| 40732. |
The decay constant of a radioactive isotope is lambda. If A_1 and A_2 are its activites at time t_1 and t_2 respectively, then the number of nuclei which have decayed the time (t_1-t_2) |
|
Answer» `A_1t_1-A_2t_2` `A_2=lambdaN_2` at time `t_2` Therefore, number of NUCLEI DECAYED during time INTERVAL `(t_1-t_2)` is `N_1-N_2=((A_1-A_2))/lambda` |
|
| 40733. |
Show the time period of oscillation when a bar magnet is kept in a uniform magnetic field is T = 2pi sqrt((l)/(p_(m)B)) . In second, where I represents moment of inertia of the bar magnet, p_(m) is the magnetic moment and is the magnetic field. |
|
Answer» Solution :The magnitude of deflecting torque ( the torque which makes the object rotate ) acting on the bar MAGNET which will tend to align the bar magnet parallel to the direction of the uniform magnetic field `vec(B)` is `|vec(tau)| = p_(m) B"sin" theta` The magnitude of restoring torque acting on the bar magnet can be WRITTEN as `|vec(tau)| = I (d^(2) theta)/(dt^(2))` Under equilibrium conditions, both magnitude of deflecting torque and restoring torque will be equal but act in the opposite directions, which means `I (d^(2) theta)/(dt^(2)) = - p_(m)" B sin " theta` the negative sign implies that both are in opposite directions. the above equation can be written as `(d^(2) theta)/(dt^(2)) = - (p_(m) B)/(I) sin theta` this is non-LINEAR second order homogeneous differential equation. In order to make it linear. we use small ANGLE approximation. i.e., sin `theta approx theta` , we get `(d^(2) theta)/(dt^(2)) = - (p_(m) B)/(I) theta` this inear second order homogeneous differential equation is a simple Harmonic differential equation. therefore, comparing with simple Harmonic Motion (SHM) differential equation `(d^(2)X)/(dt^(2)) = -omega^(2) x ` where `omega` is the angular frequency of the osxillation . `omega^(2) = (p_(m)B)/(I) rArr omega = sqrt((p_(m)B)/(I))` T = `2pi sqrt((I)/(p_(m)B))` T = `2pi sqrt((I)/(p_(m)B_(H)))` in second where, `B_(H)` is the horizontal component of Earth.s magnetic field. |
|
| 40734. |
State and explain Gauss's theorem in Electrostatics. |
|
Answer» Solution :Statement :The TOTAL electric flux through a CLOSED surface in free space is EQUAL to 1/`epsilon_(0)` 0 TIMES the net charge enclosed by the surface. Explanation: Let .q. be d1e total charge enclosed by the surface. Then, from Gauss.s .law total electric flux `phi=(q)/(epsilon_(0))` . Where `epsilon_(0)` = Permitivity of free space. |
|
| 40735. |
Why are resistances connected in series and in parallel ? |
| Answer» SOLUTION :In series to INCREASE the RESISTANCE and in PARALLEL in DECREASES. | |
| 40736. |
A slit of width d is placedinfront infront of a lensof localm the 0.5 m is determine with ligt wavelength5.89 xx10^(-2) m . The first diffraction minima on eithersideofthe centraldiffractionminimum are separatedby 2xx10^(-3) m . The fifthof the slit is : |
|
Answer» `2.945 xx10^(-4)`m |
|
| 40737. |
By "ignoring visitors", what is the poet trying to say? |
|
Answer» TIGER KNOWS his POWER is restricted |
|
| 40740. |
A string with tension T and mass per unit length mu is clamped down at x=0 and at x=L. at t=0, the string is at rest and displaced in the y-direction y(x,0)=2"sin"(2pix)/(L)+2"sin"(pix)/(L) Q. What is the total energy at t=0? |
|
Answer» `(25Tpi^(2))/(4L)` |
|
| 40741. |
In the above question the percentage loss of kinetic energy of the body during its collision with the ground is : |
|
Answer» 0.25 `Loss=("K.E. before COLLISION-K.E. sfter collision")/("K.E. before collision")XX100` =`(1/2mv_1^2-1/2mv_2^2)/(1/2mv_1^2)xx100``(because v_1=2v_2)` =`((2v_2)^2-v_2^2)/(4v_2^2)xx10` =`(3v_2^2)/(4v_2^2)xx100=3/4xx100=75%` |
|
| 40742. |
Two short bar magnets with magnetic moments 400 ab– "A cm"^2 and 800 ab – A cm^2are placed with their axis in the same straight line with similar poles facing each other and with their centres at 20 cm from each other. Then the force of repulsion is |
|
Answer» 12 DYNE |
|
| 40743. |
Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by B=0.72 (mu_(0)NI)/(R) approximately. [Such an arrnagement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils. ] |
|
Answer» Solution :Radius of two parallel co-axial coils = R, number of turns =N Current =I Let the mid pints between the coils is at point O and P be the point around the mid point O. Suppose, the distance between OP=d which is very less than `R(d LT lt R)` For the coil A, `O_(A)P=(R)/(2)+d` the magnetic field at point P DUE to coil A. `B_(A)=(mu_(0))/(4pi).(2pi nI R^(2))/((O_(A)P^(2)+R^(2))^(3//2))` `=(mu_(0))/(2). (NIR^(2))/({(Rl_(2)+d)^(2)+R^(2)}^(3//2))=(mu_(0)NIR^(2))/(2[(R^(2))/(4)+d^(2)+Rd+R^(2)]^(3//2))` as according to the question `d lt lt R`, so neglect turn `d^(2)`. `B_(A)=(mu_(0)NIR^(2))/(2[(5R^(2)=)/(4)+Rd]^(3//2))=(mu_(0)NIR^(2))/(2xx((5R^(2))/(4))^(3//2)[1+(Rxxdxx4)/(5R^(2))]^(3//2))` `=(mu_(0) NIR^(2)(1+(4d)/(5R))^(-3//2))/(2((5R^(2))/(4))^(3//2))rarr(1)` The direction of `B_(A)` is along `PO_(B)`. According to Maxwell's right hand rule for the coil `B,O_(B)P=(Rl_(2)-d)` The magnetic field at point P due to coil B `B_(B)=(mu_(0))/(4pi).(2pi NIR^(2))/((O_(B)P^(2)+R^(2))^(3//2))=(mu_(0))/(2).(2NIR^(2))/(([(R)/(2)-d]^(2)+R^(2))^(3//2))` `=(mu_(0)NIR^(2))/(2[(R^(2))/(d)+d^(2)-Rd+R^(2)]^(3//2))=(mu_(0)NIR^(2)(1-(4d)/(5R))^(-3//2))/(2((5R^(2))/(4))^(3//2))` The direction of magnetic field `B_(B)` is TOWARDS `PO_(B)`. S0, the resultant magnetic field at P due to coil A and coil B is `B=B_(A)+B_(B)=(mu_(0)NIR^(2))/(2((5R^(2))/(4))^(3//2)).[(1+(4d)/(5R))^(-3//2)+(1-(4d)/(5R))^(-3//2)]` Now, use binomial theorem and neglect higher power as `d lt lt R` `B=(mu_(0)NIR^(2))/(2((5R^(2))/(4))^(3//2))[1-(3)/(2)xx(4d)/(5R)+1+(3)/(2)xx(4d)/(5R)]` `=(mu_(0)NI)/(2R)((4)/(5))^(3//2)xx2` `=((4)/(5))^(3//2).(mu_(0)NI2)/(2R)=(2mu_(0)NI)/((5)^(3//2).2R)(4)^(3//2)` `=0.72. (mu_(0)NI)/(R)` 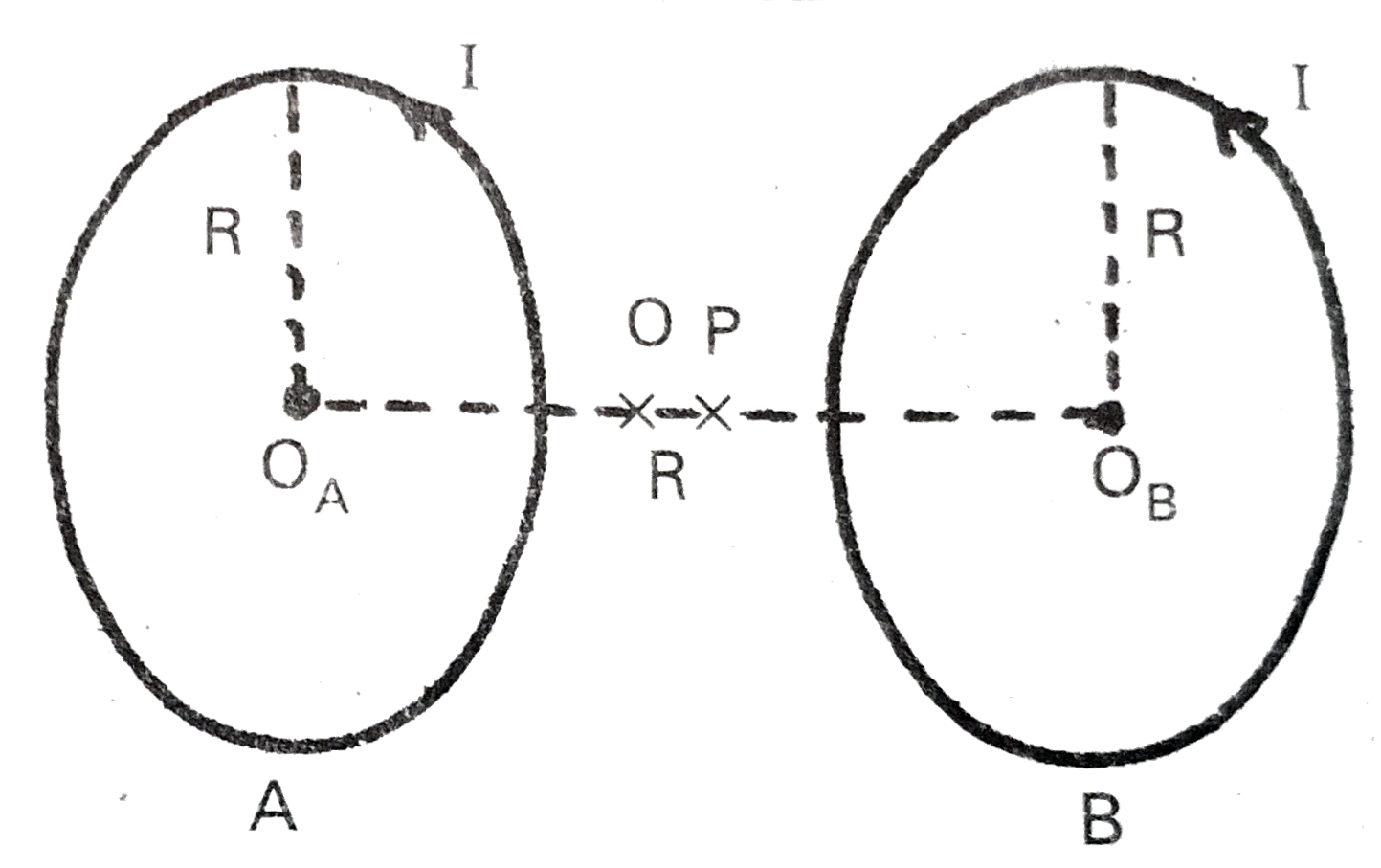
|
|
| 40744. |
A wire in the form of a square side a carries a current I. Then the magnetic induction at the centre of the square is (magnetic permeability of freespace=mu_(0)) |
|
Answer» `(mu_(0)i)/(2pia)` |
|
| 40745. |
The simplified Y output of the given logic circuit is |
|
Answer» `BAR(A). B + A .bar(B)` |
|
| 40746. |
The possible quantum numbers for 3d electrons are |
|
Answer» `n=3, l=1, m_(1)=+1, m_(s)=-1/2` |
|
| 40747. |
Obtain the equation of magnification for compound microscope. |
Answer» Solution : Linear MAGNIFICATION due to the objective, `m_0=(h.)/(h)` where h. is dimension of first image. `h_0` is dimension of object. Here,tan`beta=(h)/(f_0) implies h= f_0tan beta ` … (1) and `tan beta=(h.)/(B_1B.)` `implies h.=L tan beta`...(2) [`because B_1B.=L]` `therefore m_0=(h.)/(h)=(Ltan beta)/(f_0tan beta)=(L)/(f_0)` `therefore m_0 =(L)/(f_0)` ...(3) When the FINAL image is formed at the near point is, `m_e=1+(D)/(f_e)` when the final image is formed at infinity, the angular magnification due to the eyepiece, `m_e=(D)/(f_e)` ...(4) Thus, the total magnification, `m=m_0m_e=((L)/(f_0))((D)/(f_e))` To ACHIEVE a large magnification of a small object (hence the name microscope), the objective and eyepiece should have small focal lengths. VARIOUS other factors such as illumination of the object contribute to the quality and visibility of the image. In modern microscopes, multicomponent lenses are used for both the objective and the eyepiece to improve image quality by minimising various optical ABERRATIONS (defects) in lenses. |
|
| 40748. |
अभिकथन: चंद्रमा पर गुरुत्वीय त्वरण धरती की तुलना में छठवाँ भाग होता है। तर्कः गुरुत्वाकर्षण का नियम, चंद्रमा एवं धरती दोनों पर ही समान है | |
|
Answer» अभिकथन और तर्क दोनों सही हैं तथा तर्क, अभिकथन की सही व्याख्या करता है। |
|
| 40749. |
What is the de Broglie wavelength of the electron accelerated through a potential difference of 100 volt ? |
|
Answer» `12.27 Å` |
|
| 40750. |
What is logic gate? |
|
Answer» SOLUTION :A logic GATE called the digital circuit of something more important than certain types of logic functions. A gate is a digital circuit that followscertain logical relationship between the input and output voltages. They are known as logic gates. Gates because they control the flow of information. The five common logic gates used are NOT, AND, OR, NAND, NOR. Each logic gate is indicated by a symbol and its FUNCTION and its behaviour is understandable with this truth table. Means, truth table is useful for understanding the behaviour of logic gate. Truth table: It is a table that shows all possible input combinations and the CORRESPONDING output combination for a logic gate. The Boolean equation is called the logic representation of a particular types of logic gate operation. SEMICONDUCTOR devices are useful to understand the function of logic gate. |
|



