Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 40751. |
When photons of energy 5 eV fall on the surface of a metal, the emitted photoelectrons are stopped by a cut off potential of 1.6V. The work function of given metal is______. |
| Answer» Solution :3.4 EV. [Work FUNCTION `phi_(0)=E-eV_(0)=5eV-1.6eV=3.4eV`]. | |
| 40752. |
Write the expression for the half life of a radioactive element. |
|
Answer» Solution :After ONE half LIFE `t=T_(1//2) rArr N= N_(0) //2` USING the RELATION `N= N_(0) e^(-lambda t)` `rArr N_(0) //2 = N_(0) e^(- lambda T_(1//2) )` `rArr 1//2 = e^(-lambda T_(N))` `rArr lambda T_(1//2) = log_(n) 2` `rArr lambda T_(1//2) = 0.693 ` Arriving at `T_(1//2) = (0.693)/(lambda) ` |
|
| 40753. |
A charge of 2 xx 10^(-2)C moves at 30 revolutions per second in a circle of diameter 80 cm. The current linked with the circuit is ..... |
|
Answer» Solution :0.60 A `omega = 30 " rad /s "= 60 PI" rad /s"` `I= (Q)/(T) = (Q omega)/(2 pi)"" [ because T = (2pi)/(omega) ] ` `therefore I = ( 2 XX 10^(-2) xx 60 pi)/(2 pi ) = 60 xx 10^(-2) A = 0.6 A ` |
|
| 40754. |
The ratio of radii of planets A and B in K_(1) and ratio of accelerations due to gravity on them is K_(2). The ratio of escape velocities from them will be |
|
Answer» `K_(1)K_(2)` Given `R_(1)//R_(2)=K_(1),(g_(1))/(g_(2))=K_(2)` `:. (v_(1))/(v_(2))=sqrt((2Rg_(1)g_(2))/(2R_(2)g_(2)))=sqrt((R_(1))/(R_(2)).(g_(1))/(g_(2)))=sqrt((K_(1)K_(2)))` |
|
| 40755. |
Three amplifiers each with a voltage gain of 10 are connected in series. Then overall amplification is : |
|
Answer» `10/3` `=10xx10xx10` = 1000 `:.` OVERAL amplification = 1000 |
|
| 40756. |
Photocell is kept at distance of 1 m from the source and incident radiation .Now distance from source is changed to 2m,then…. |
|
Answer» no. of PHOTOELECTRON emitted are `(1)/(4)` times intital value. Power `prop(1)/(2)impliesNprop (1)/(r^(2))` |
|
| 40757. |
मान लीजिए की R द्विआधारी संख्याa*b=1+ab,a,b in R तो संक्रिया |
|
Answer» क्रम विनिमेय है किन्तु साहचर्य नहीं है । |
|
| 40758. |
VARIATION OF BINDING ENERGY OF PER NUCLEON WITH MASS NUMBER |
|
Answer» Solution :Modulation INDEX `=A_(m)//A_(c)=20//40=0.5` The SIDE bands are. (2000+200)KHz =2020 KHz and (2000-20) KHz =1980 KHz AMPLITUDE versus w for amplitude MODULATED SIGNAL: |
|
| 40759. |
When a wire of uniform cross-section, having resistance R, is bent into a complete circle, the resistance between any two of diametrically opposite points will be |
|
Answer» `(R )/(8)` |
|
| 40760. |
If the speed of light in material A is 1.25 times its speed in material B then the ratio of he refractive indices of these materials is |
|
Answer» a. 1.5 |
|
| 40761. |
Obtain an expression for the magnetic field at a point due to an infinitely long thin conductor or wire by applying Ampere's circuital law. |
|
Answer» Solution :LET I be the current in the wire PQ. Let P be a point at a PERPENDICULAR distance r from the wire. Let dI be the element of length of the closed path. The direction of the magnetic FIELD will be tangential to the point P on the element. APPLYING Ampere's circuital law, we have `""ointvec(B).dvec(l)=mu_(0)I` i.e., `""ointBdlcos0^(@)=mu_(@)I, ""theta=0^(@)` between tangent drawn at P to the element of length dl and `vec(B)`. Thus `""Bointdl=mu_(@)I` or `""B=(mu_(0)I)/(ointdl)=(mu_(0)I)/(2pir)` Thus `""B propto 1/r` Note : B along the axis of the wire = 0 
|
|
| 40762. |
A cell has an emf of 1.5V. When short circuited, it gives a current of 3A. The internal resistanceof the cell is |
|
Answer» `0.5Omega` |
|
| 40763. |
Needle N_1 , N_2 and N_3 are made of ferromagnetic , a paramagnetic and a diamagnetic substance respectively. A magnet when brought close to them will |
|
Answer» Attract all THREE of them Needle `N_(2)` is PARAMAGNETIC Needle `N_(3)` is diamagnetic |
|
| 40764. |
For an RLC circuit driven with voltage of amplitude v_m and frequencyomega_0=1/sqrt(LC) the current exibits resonance. The quality factor, Q is given by : |
|
Answer» `(omega_0L)/R` |
|
| 40765. |
If 10^(9) electrons move out of a body to another body every second, how much time is required to get a total charge of 1 C on the other body ? |
|
Answer» Solution :If no. of electrons TRANSFERRED from first body to second body in UNIT TIME is `N/t` then total CHARGE transferred in t. time will be, `Q(N/t) xx t. xx e` `therefore 1 = 10^(9) xx t. xx 1.6 xx 10^(-19)` `therefore t. =1/(1.6 xx 10^(-10)) = 10^(10)/1.6s` `therefore t. = 198.2` year |
|
| 40766. |
Although ordinary rubber is insulator, the rubber tyres of air crafts are made slightly conducting. Why? |
| Answer» Solution : During the take off and LANDING, the friction between TYRES and the run-way CAUSES ELECTRIFICATION of tyres. If the tyres are non-conducting, excessive charge will accumulate on the tyres which may cause sparking. If the material of the tyres is slightly conducting, the accumulated charge can flow to earth, thus eliminating any danger of fire. | |
| 40768. |
Aninfinitenumber of charges each of value Q are palced on thex-axisat distances of1, 2, 4, 8, ….. meterfrom the origin. If the charges are alternately positiveand negativefind the electric field (Intensity of electricfield) at origin. |
|
Answer» Solution :The electric field `E = (Q)/( 4 pi in_(0)) (1- (1)/(2^(2)) +(1)/(4^(2))-(1)/(8^(2)) + ……) ` `= (Q)/( 4 pi in_(0)) (1)/([ 1 - ((-1)/(4))]) =(Q)/( 4pi in_(0)) . (4)/(5)` SINCE the expressionin thebracketis in GP with a common RATIO `=(1)/(2^(2)) = (1)/(4)`. `E =(4)/(5) . (Q)/( 4pi in_(0)) ` `E = (Q)/( 5 pi in_(0))` |
|
| 40769. |
A plano concave lens is silvered at the plane surface. How does it behave? |
|
Answer» SOLUTION :It BEHAVES like a convex mirror. NOTE: `(1)/(F)=- (1)/(f)+(1)/(f_(m))- (1)/(f)` `(1)/(F)= (2)/(f)"" because r =OO, f_(m)=oo` for a plane surface `F=(-f)/(2)` |
|
| 40770. |
If a coil of area 0.15m^(2) and 50 turns is perpendicular to a magnetic field, which changes from 5xx10^(-3) to 2xx10^(-3)T in 30 ms. Calculate the induced e.m.f. |
|
Answer» SOLUTION :`A=0.15m^(2),N=50,dt=30xx10^(-3)s` `dB=2xx10^(-3)-5XX10^(-3)=-3XX10^(-3)T` `dphi_(B)=A.dB=0.15xx(-3xx10^(-3))=-0.45xx10^(-3)Wb` `varepsilon=-N(dphi_(B))/(dt)=(-50xx(-0.45xx10^(-3)))/(30xx10^(-3))=0.75V` |
|
| 40771. |
A black body at a temperature of 127^(@)C radiates heat at the rate of 5 cal/cm^(2)s at a temperature of 927^(@)C, its rate of emission in units of cal/cm^(2) s will be nearly |
|
Answer» 405 `E_(2)=81xx5=405`. |
|
| 40772. |
A plane light wave wityh wavelength 0.60 mu m falls normally on a long opaque strip 0.70 mm wide. Behind it a screen is placed at a distance 100cm. Using Fig. find the ratio of intensities of light in the middle of the diffraction pattern and at the edge of the geometrical shadow. |
Answer» Solution :We shall use the equation written down in `5.103`, the Fresnel-Huyghens FORMULA.  Suppose we want to find the intensity at `P` which is such that the corrdinates of the edges (x-coordinates) with respect to `P` are `x_(2)` and `-x_(1)`. Then, the amplitude at `P` is `E = intK(varphi) (a_(0))/(r )e^(-ikr) dS` We write `dS = dxdy, y` is to integrated from `-oo + 0 + oo`. We write `r = b + (x^(2) + y^(2))/(2b) .......(1)` `(r` is the disatnce of the element of surface on `I` from `P`. It is `sqrt(b^(2) +x^(2) + y^(2))` and hence appoximately (1)). Wer then get `E = A_(0)(b) [int_(0)^(oo) e^(-ikx^(2)//2b) dx + int_(-oo)^(-x_(1))e^(-ikx^(2)//2b)dx]` `= A'_(0)(b) [int_(v_(2))^(oo) e^(-i)(piu^(2))/(2)du+ int_(-oo)^(-v_(1)) e^(-ipiu^(2)//2 du)]` where `v_(2) = sqrt((2)/(b lambda))x_(2), v_(1) sqrt((2)/(b lambda))x_(1)` The intensity is the SQUARE of the amplitude. In our case, at the centre `v_(1) = v_(2) = sqrt((2)/(b lambda)).(a)/(2) = sqrt((a^(2))/(2b lambda)) = 0.64` `(a =` width of the STRIP `= 0.7 mm, b = 100CM, lambda = 0.60mu m)` At, say, the lower edge `v_(1) = 0, v_(2) = 1.28` Thus `(I_(centre))/(I_("edge")) =|(int_(0.64)^(oo) e^(-IPI u^(2)//2)du + int _(-oo)^(0.64)e^(-ipiu^(2)//2) du)/(int_(1.28)^(oo) e^(-ipi u^(2)//2)du + int_(-oo)^(0)e^(-ipiu^(2)//2) du)|^(2) = 4(((1)/(2)-C(0.74))^(2) + ((1)/(2)-S(0.64))^(2))/(1-C(1.28)^(2)+(1-S(1.28))^(2))` where `C(v) = int_(0)^(v) cos .(piu^(2))/(2)du` `S(v) = int_(0)^(v) sin. (piu^(2))/(2)du` Rough evaluation of the intergrals using corn's spiral gives `(I_(centre))/(I_("edge")) ~~2.4` (We have used `int_(0)^(oo) cos. (piu^(2))/(2)du =int_(0)^(oo) sin. (piu^(2))/(2)du = (1)/(2)` `C(0.64) = 0.62, S(0.64) = 0.15` `C(1.28) = 0.65 S(1.28) = 0.67` |
|
| 40773. |
A person wit a normal near point (25 cm) using a compound microscope with objective of focal length 8.0 mm and an eyepiece of focal length 2.5 cm can bring object placed at 9.0 mm from the objective in sharp focus. What is the separation between the two lenses ? Calculate the magnifying power of the microscope. |
|
Answer» Solution :`F_(0) = 8 mm= 0.8, f_(e) = 2.5 `cm D = 25 cm , `v_(e) - D = - 25 cm, u_(e) = - 9MM = 9.0 `cm `m_(e) = (v_(e))/(u_(e)) = 1 + (D)/(f_(e)) "" (-25)/(u_(e)) = 1 + (25)/(2.5) = 11"" therefore u_(e) = (-25)/(11) cm` `(1)/(v_(0)) - (1)/(u_(0)) = (1)/(f_(0))` `(1)/(v_(0)) = (1)/(f_(0)) + (1)/(u_(0)) = (1)/(0.8) + (1)/(-0.9) "" therefore v_(0) = 7.2 ` cm Separation between lenses = `|u_(e)| + |v_(e)| = (25)/(11) + 7.2 = 9.47 cm ` `M = (v_(0))/(-u_(0))[ 1 + (D)/(f_(e)) ]= (72)/(0.9) (1 + (25)/(2.5) ) = 88` |
|
| 40774. |
A capacitor of capacity 2muF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 0.2mH. At an instant when potential difference across the capacitor is 6v |
|
Answer» current in the circuit is 1.04A |
|
| 40775. |
What is tringe width ? |
| Answer» Solution :The distance between any two MAXIMA or minima in CONSTRUCTIVE or distructive INTERFERENCE is CALLED fringe width given by `beta = (lambda D)/d`. | |
| 40776. |
1 curie represents |
|
Answer» `3.7 xx 10^7` DISINTEGRATIONS per SECOND |
|
| 40777. |
In the figure shown. Find the e.m.f. varepsilon for which charge on 2mu F capacitor is 4 mu C. |
|
Answer» |
|
| 40778. |
Define the term: magnetic dipole moment of a current loop. Write the expression for the magnetic moment when an electron revolves at a speed v around an orbit of radius r in hydrogen atom. |
|
Answer» Solution :The product of the current in the LOOP to the area of the loop is the magnetic dipole MOMENT of a current loop. The magnetic moment of electron `BAR(mu)= - (e )/(2) (overset(to) (R ) xx overset(to) (V) ) = - (e )/(2m_(0)) (overset(to)(r ) xx overset(to) (p) )=- (e)/(2m_(0)) overset(to)(l)` |
|
| 40779. |
The frequency response curve for the filter circuit used for production of AM wave should be |
|
Answer» (i) FOLLOWED by (ii) |
|
| 40780. |
Which of the following is compared to senses? |
|
Answer» DEEPEST fear |
|
| 40781. |
State Lenz.s Law. A metallic rod held horizontally along east-west direction, is allowed to fall under gravity. Will there be an emf induced at its ends? Justify your answer. |
|
Answer» Solution :The polarity of induced EMF is such that it TENDS to produce a current which opposes the change in magnetic FLUX that produced it. YES, as the magnetic flux due to vertical component of Earth.s magnetic field keeps on CHANGING as the metallic rod falls down. |
|
| 40782. |
The unit of radioactivity decay rate is |
|
Answer» Curie |
|
| 40783. |
The study of trends in human population growth and the prediction of the detailed Information of population with different age group is known as- |
|
Answer» Sociology |
|
| 40784. |
The activity of a radioactive sample is measures as N_0 counts per minute at t = 0 and N_0//e counts per minute at t = 5 min. The time (in minute) at which the activity reduces to half its value is. |
|
Answer» `log_e2/5` `R=R_0e^(-lambdat)` …(i) where, `R_0`=initial activity at t=0 R=activity at time t `lambda`=decay constant According to GIVEN problem, `R_0=N_0` counts per minute `R=N_0/e` counts per minute t=5 minutes Substituting these VALUES in equation (i), we get `N_0/e=N_0e^(-5lambda)` `e^(-1)=e^(-5lambda)` `5lambda=1` or `lambda=1/5` per minute At `t=T_(1//2)` , the activity R reduces to `R_0/2`. where `T_(1//2)` = half life of a radioactive sample From equation (i), we get `R_0/2=R_0 e^(-lambdaT_(1//2))` `e^(lambdaT_(1//2))=2` Taking natural logarithms on both sides of above equation, we get `lambdaT_(1//2) = log_e2` or `T_(1//2)=(log_e 2)/lambda=(log_e 2) /((1/5))=5 log_e 2` minutes |
|
| 40785. |
A series LCR circuit is connected to an a.c. source having voltage V=V_(m) sin omega t Derive the expression for the instantaneous current I and its phase relationship to the applied voltage. Obtain the condition for resonance to occur. Define 'power factor'. State the conditions under which it is (i) maximum, (ii) minimum. |
Answer» Solution : Let as shown in Fig. 7.42 an alternating voltage`V = V_(m) sin omega t`be applied across a series combination of an inductor L, capacitor C and resistance R. As all components are in series, same current I flows through them. Let `vecV_(L), vecV_(C)` and `vecV_(R)` represent the instantaneous across L,C and R respectively, where (i) `vecV_(L) = IX_(L)` and leads the current in phase by `pi/2`. (ii) `vecV_( c) = IX_( c)` and lags behind the current by `pi/2`, and (iii) `vecV_(R) = IR` in same phase as the current I. The VOLTAGES are shown in phasor diagram in Fig. 7.43. Since `vecV_(L)` and `vecV_( c)`are in mutually opposite phase, they can be combined into a single phasor having magnitude `(V_(L)-V_(C))`and leading the current by `pi/2` Resultant of `V_(R)` and `(V_(L)-V_(C))`gives the total voltage, which is equal to the voltage of a.c. source. Thus, `V = sqrt(V_(R)^(2) + (V_(L)-V_( C))^(2)) = sqrt((IR)^(2) + I(X_(L)-X_(C))^(2))` `=I sqrt(R^(2) + I(X_(L) -X_(C))^(2))` `=I sqrt(R^(2) + (X_(L)-X_(C))^(2)) = IZ`  where Z is known as the impedance of given LCR series circuit. Hence, impedance `Z = sqrt(R^(2) + (X_(L)-X_(C))^(2))` `= sqrt(R^(2) + (L omega -1/(C omega)^(2))` Moreover, the voltage leads the current (or current lags behind the voltage) by a phase angle `phi`such that `tan phi =(V_(L)-V_(C))/V_(R) =(X_(L)-X_(C))/R = (Lomega-1/(Comega))/R` Thus, current in the circuit is given by `I = V/Z sin(omega t - phi)`, where `Z= sqrt(R^(2) + (X_(L)-X_(C))^(2))` and `phi = tan^(-1) (X_(L)-X_(C))/R`. The current amplitude `I_(m) = V_(m)/Z` Condition for Resonance and Resonant Frequency : Impedance of the given a.c. circuit will be MINIMUM and the current maximum if `X_(L) = X_( C)`because then Z = R and `I =V/R`. It is called resonance condition. For resonance to happen angular frequency of a.c. should be `omega_(0)`), so that `X_(L) = (L omega_(0)) = X_(C) = (1/(C omega_(0))) rArr omega_(0) = 1/sqrt(LC)` Power factor of an a.c. circuit is the cosine of the angle (cos ) by which the current lags or leads the a.c. voltage. Power factor, `cos phi = R/sqrt(R^(2) + (Lomega - 1/(C omega)^(2))) = R/sqrt(R^(2) + X^(2))` (i) The power factor is maximum, having a value one, when either the circuit is purely resistive circuit or when `X_(L) = X_(C)`so that Z=R. (ii) The power factor is minimum, having a value zero, when no resister R is PRESENT in the circuit and impedance is purely reactive impedance |
|
| 40786. |
The magnetic field due to a current-carrying loop of radius 3 cm at a point on its axis at the distance of 4 cm from the centre is 54μ T. What will be its value at the centre of the loop ? |
|
Answer» `250muT` |
|
| 40787. |
How mean value of ac and instanttaneously current are mathematically related ? |
| Answer» SOLUTION :Arithmatic MEAN | |
| 40788. |
(i) Why does the sun appear reddish at sun-set or sun- rise ? (ii) For which colour the refractive index of prism material is maximum and minimum ? |
|
Answer» Solution :(i) At sun-set or sum-rise, the sun's rays have to pass through a larger DISTANCE in the atmosphere Most of the BLUE and other shorter WAVELENGTH are removed by scattering. The least SCATTERED light reaching our eyes , therefore, the sun looks reddish. (ii) Refractive index of prism material is (a) MAXIMUM for violet colour and (b) minimum for red colour. |
|
| 40789. |
A unifrom rope of mass 0.1kg and length 2.45 m hangs from a rigid support. The time taken by the transverse wave formed in the rope to travel through the full length of the rope is (Assume g==9.8 m//s^2) |
|
Answer» |
|
| 40790. |
In a photodiode the value of current produced, when monochromatic light of suitable is incident on the junction, depends on |
|
Answer» the frequency of incident light. |
|
| 40791. |
According to kinetic theory, the collisions between molecules of a gas are- |
|
Answer» PERFECTLY elastic |
|
| 40792. |
The following logic symbol represents |
|
Answer» an OR GATE |
|
| 40793. |
Some aliens living beneath the surface of the earth want to send a parcel to their friends just outside earth's pull. What should bethe velocity with which they must throw the parcel from a depth ofR/2? |
|
Answer» 11.2 km/s |
|
| 40794. |
In the young's double slit experiment the intensity of light at a point on the screen where the path difference is lamda is K, (lamda being the wavelength of light used). The intensity at a point where the path difference is lamda//4. Will be: |
|
Answer» K |
|
| 40795. |
Three capacitors A,B,C are connected in such a way that their equivalent capacitance is equal to the capacitance of B. The capacitances of A and B are 10 muF " and " 30muF respectively and C ne 0. Determine three possible values of C and also show how the capacitors are to be connected in the three cases. |
Answer» SOLUTION :The CAPACITOR B cannot be joined in parallel to any combination of the capacitors A and C because in that case equivalent capacitance will be greater than the capacitance of B. The following THREE combination are POSSIBLE. 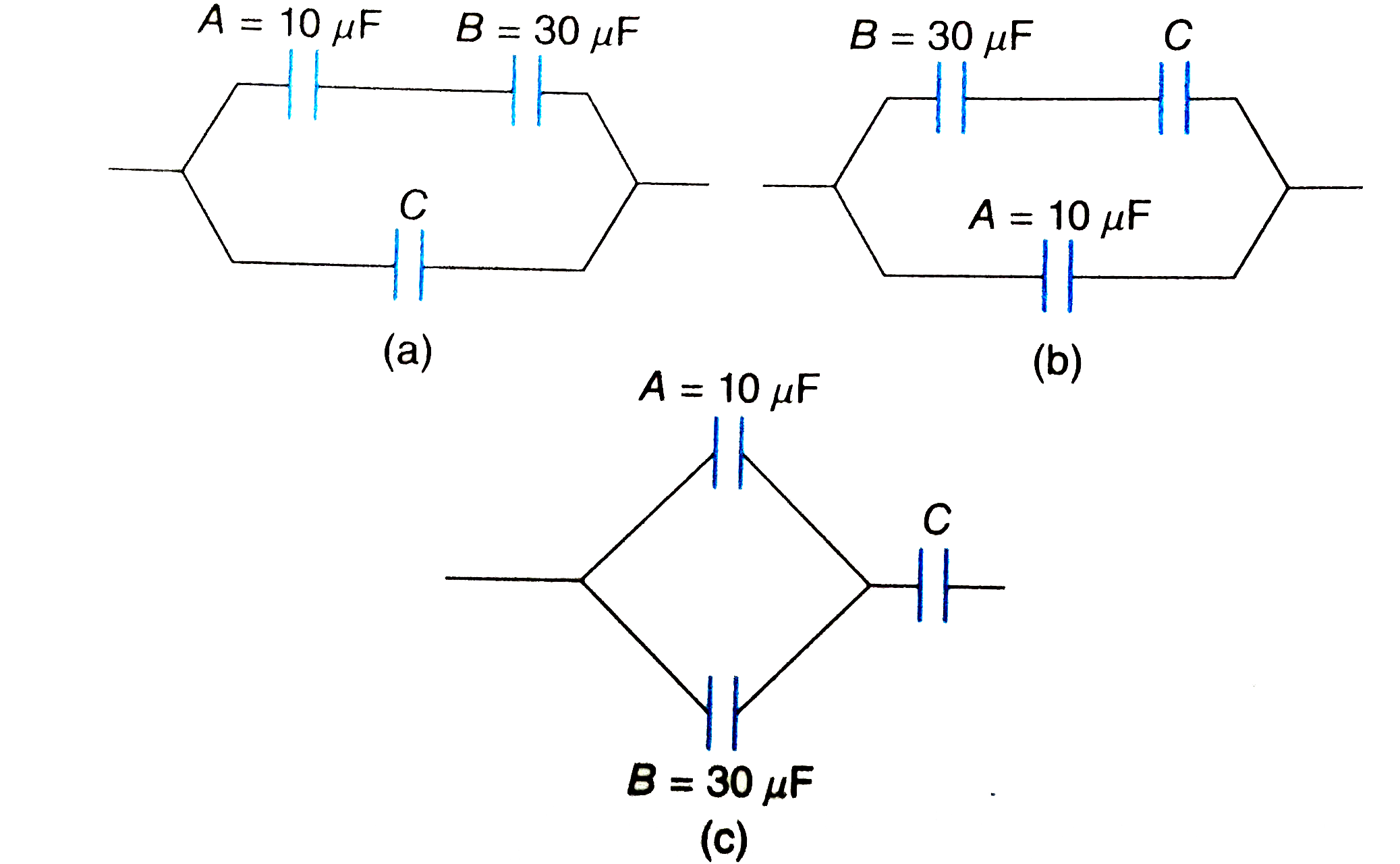 i) A and B are connected in series. Now C is connected in parallel with the series combination of A and B. ACCORDING to the question, `(10xx30)/(10+30) +C= 30 " or, "(300)/(40)+C=30` or, `C= 22.5muF` ii) B and C are connected in series. Now A is connected in parallel with the series combination of B and C. According to the question, `(30xxC)/(30+C)+10=30 " or, "(30xxC)/(30+C)=20` or, `C 60muF` iii) A and B are connected in parallel. Now C is connedted in series with the parallel combination of A and B. According to the question, `(40xxC)/(40+C)=30 " or "3(40+C) =4C " or "C= 120muF`. |
|
| 40796. |
A cone of radius r and height h is kept on a turntable rotating with an angular velocity. The friction between te table and the cone is sufficient so that the cone does not slide. The distance between the axis of the cone and the axis of turntable is R(Rgtgtr). the maximum value of omega for which the cone does not topple is sqrt((xgr)/(Rh)), calculate x. |
| Answer» Solution :`m omega^(2)R((H)/(4))=mgrrArromega=sqrt((4gr)/(Rn))` | |
| 40797. |
What produces electromagnetic waves ? |
| Answer» SOLUTION :ACCELERATED CHANGE | |
| 40798. |
The distance travelled by light in glass (refractive index =1.5)in a nanosecond will be |
| Answer» Answer :d | |
| 40799. |
Electro motive force represents |
|
Answer» force |
|
| 40800. |
Two point charges +8q) and (-2q are located at , v = 0 and ,v = L respectively. The location of a point on the v-axis at which the et electric field due to these two point charges b is zero: |
|
Answer» 4L |
|