Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 41301. |
The half-life of " "_(53)^(131)I is 8 days. Give a sample of " "_(53)^(131)I at time t = 0, we can assert that |
|
Answer» no NUCLEUS will DECAY before t = 4 days |
|
| 41302. |
A particle of mass 1 Kg and carrying 0.01 C is at rest on an inclined plane of angle 30^@ with horizontal when an electric field of (490)/(sqrt(3)) NC^(-1) applied parallel to horizontal, the coefficient of friction is |
|
Answer» `0.5` |
|
| 41303. |
A hollow cylinder is kept in 3-dimensional coordinate system of lm length and 25 cm^2 cross sectional area. Electric field in this region is vecE = 50 xhati N/C where, x is in m, then find (i) Net flux in cylinder. (ii) Net charge enclose by cylinder. |
|
Answer» |
|
| 41304. |
A 100W-220V bulb is connected to 110 V source. Calculate thepower consumed by the bulb. |
|
Answer» Solution :POWER of the BULB, `P=100W` Operating voltage, `V=200V` Resistance of the bulb, `R=(V^(2))/(P)=((200)^(2))/(100)=484Omega` Actual operating voltage, `V^(1)=100V` Therefore, power consumed by the bulb, `P^(1)-((V^(1))^(2))/(R )=((100)^(2))/(484)=25W`. |
|
| 41305. |
In RLC series AC circuit at resonance : |
|
Answer» Resitance is zero |
|
| 41306. |
In photoelectric effect for emission of electron incident light should have minimum …… |
|
Answer» wavelength |
|
| 41308. |
A vessel of volume V contains a mixture of hydrogen and helium a ta temperature T and pressure p. The mass of themixtureis equalto m . Findthe ratio of the mass of hydroge tothatof heliumin the given mixture. Takemolarmasses hydrogenand heliumot be M_(1)and M_(2)respectively . |
| Answer» SOLUTION :`[m_(1) //m_(2)= (1- a//m_(2)) //(alM_(2) - 1) = 0.50, ` WHEREA= mRt/pV] | |
| 41309. |
Nanukaka was related to the narrator,as he was his- |
|
Answer» uncle |
|
| 41310. |
When light of a certain wavelength is incident on a plane surface of a material at a glancing angle 30^@, the reflected light is found to be completely plane polarized Determine Angle of refraction. |
|
Answer» Solution :From Snell.s law `MU= (sin i)/(sin r)""therefore sqrt(3)= (sin 60^(@))/(sin r)` or `sin r = (sqrt(3))/(2)xx (1)/(sqrt(3))= (1)/(2), r= 30^(@)`. |
|
| 41311. |
Define resolving power of an astronomical refracting telescope and write expression for it in normal adjustment. Assume that light of wavelength 6000Å is coming from a star, what is the limit of resolution of a telescope whose objective has a diameter of 2.54 m? |
|
Answer» Solution :The resolving power of a TELESCOPE is its ability to show as distinct (separate) two light rays coming from nearby points of an astronomical. Mathematically, resolving power of telescope is reciprocal of its limit of resolution. In normal adjustment of an astronomical telescope resolving power `=(1)/(Delta THETA)=(A)/(1.22lambda)`, whereA is the APERTURE of telescope objective and `lambda` the wavelength of light. Here `lambda=6000Å=6000xx10^(-10)m and A=2.54m` `therefore"Limit of resolution "Delta theta=(1.22lambda)/(A)=(1.22xx(6000xx10^(-10)))/(2.54)=2.88xx10^(-7)" RAD"` |
|
| 41312. |
When a metallic surface is illuminated with radiation of wavelength lambda,the stopping potential is V.If the same surface is illuminated with radiation of wavelength 2lambda,the metallic surface is |
|
Answer» 5 `LAMBDA` `EV=(hc)/(lambda)-(hc)/(lambda_(0))` For second case `e(V)/(4)=(hc)/(2lambda)-(hc)/(lambda_(0))` `therefore eV=(2hc)/(lambda)-(4hc)/(lambda_(0))` ……..(2) By comparing (1) and (2) `therefore (hc)/(lambda)-(hc)/(lambda_(0))=(2hc)/(lambda)-(4hc)/(lambda_(0))` `therefore (hc)/(lambda)-(2hc)/(lambda)=(hc)/(lambda_(0))-(4hc)/(lambda_(0))` `therefore -(hc)/(lambda)=-(3hc)/(lambda_(0))` `therefore -(hc)/(lambda)=-(3hc)/(lambda_(0))` `therefore lambda_(0)=3lambda` |
|
| 41313. |
A particle vibrates harmonically at a frequency of 0.5 Hz. At the initial moment it is in an equilibrium position moving at a speed of 20 cm/s. Write down the equation of the vibrations. |
|
Answer» The particle.s velocity is `v=-Aomegasin(omegat+varphi)`. The initial velocity `v_(0)=-Aomegasinvarphi=0.20` is, according to the statement to the problem, a POSITIVE quantity, and this is possible only if `varphi=3pi//2`. Hence, `Aomega=0.2`. But `omega=2piv=pi` rad/s. Hence the amplitude is `A=0.20//pi=0.064m`. Knowing the amplitude, the frequency and the initial phase we MAY easily wirte down the equation of the oscillations. |
|
| 41314. |
List-IList-II a) Fresnel.s diffractione) Bring band b) Fraunhofer.s sdiffractionf) Source and screen are at finite distance c) In interference phase difference is even multiple of pig) Dark band d) In interference phase difference is odd multiple of pih) Source and screen are at infinite distance |
|
Answer» `A-F, B-H, C-E, D-G` |
|
| 41315. |
Two separate segments of equal area are isolated in the energy distribution of black body radiation (As shown in the following figure). Let us assume that the number of photons emitted by the body per unit time in the segments is n_(1) and n_(2) and the energy of the photons are E_(1) and E_(2) respectively. Then |
|
Answer» `n_(1)gtn_(2)` |
|
| 41316. |
If the angle of prism is 60^@ and angle of minimum deviation is 40^@. Then the angle of refraction is |
| Answer» ANSWER :B | |
| 41317. |
What is torque on a dipole ? |
|
Answer» Solution :When a MEGNETIC dipole is freely SUSPENDED in an UNIFORM magnetic field, it is acted upon by a TORQUE given by `tou=vec M xx vec B= MB sintheta` where M is dipole MOMENT. |
|
| 41318. |
In the following common emitter configuration an NPN transistor with current gain beta = 100 is used . The output voltage of the amplifier will be |
|
Answer» Solution :`V_("INPUT")=10^(-3)V, beta=100` `V_("out")= beta xx "Input"=100 xx10^(-3)=0.1V` |
|
| 41319. |
A circular loop of metal wire of radius r is placed perpendicular to uniform magnetic field B. Half of the loop is folded about the diameter with constant angular velocity omega. If resistance of the loop is R then current in the loop is |
|
Answer» zero, when `theta = 0` `phi= B xx (pi)/(2)+ Bxx (pir^(2))/(2) xx cos omegat` Magnitude of the emf induced can be written as follows: `E= |(dphi)/(dt)|= (Bpir^(2))/(2) xx omega sin omegat` `e= (B omegapir^(2))/(2) sin omegat` Or in terms of `theta` we can write it as follows: `e= (B omegapir^(2))/(2) sin sintheta` Current Clowing through the coil can be written as follows: `i= (e)/(R)` `implies i= (pir^(2)B omega)/(2R)sintheta` We can SEE that options (a) and (d) are correct. |
|
| 41320. |
The frequency of third overtone of a closed pipeis in unison with the fifth overtone of an open pipe. What is the ratio of their lengths/ |
|
Answer» 0.3 |
|
| 41321. |
In a single slit diffraction experiment when a tiny circular obstacle is placed in the path of light from a distance source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why ? State two points of difference between the interference pattern in Young's double slit experiment and the diffraction pattern due to a slit. |
Answer» SOLUTION :In a SINGLE slit diffraction experiment when a tiny circular obstacie is placed in the path of light from a DISTANCE source, a bright spot is seenat the centre of the shadow of the obstacle. Because the waves diffracted from the edges interfere interfere constructively at the centreof shadow thus forming bright spot there. 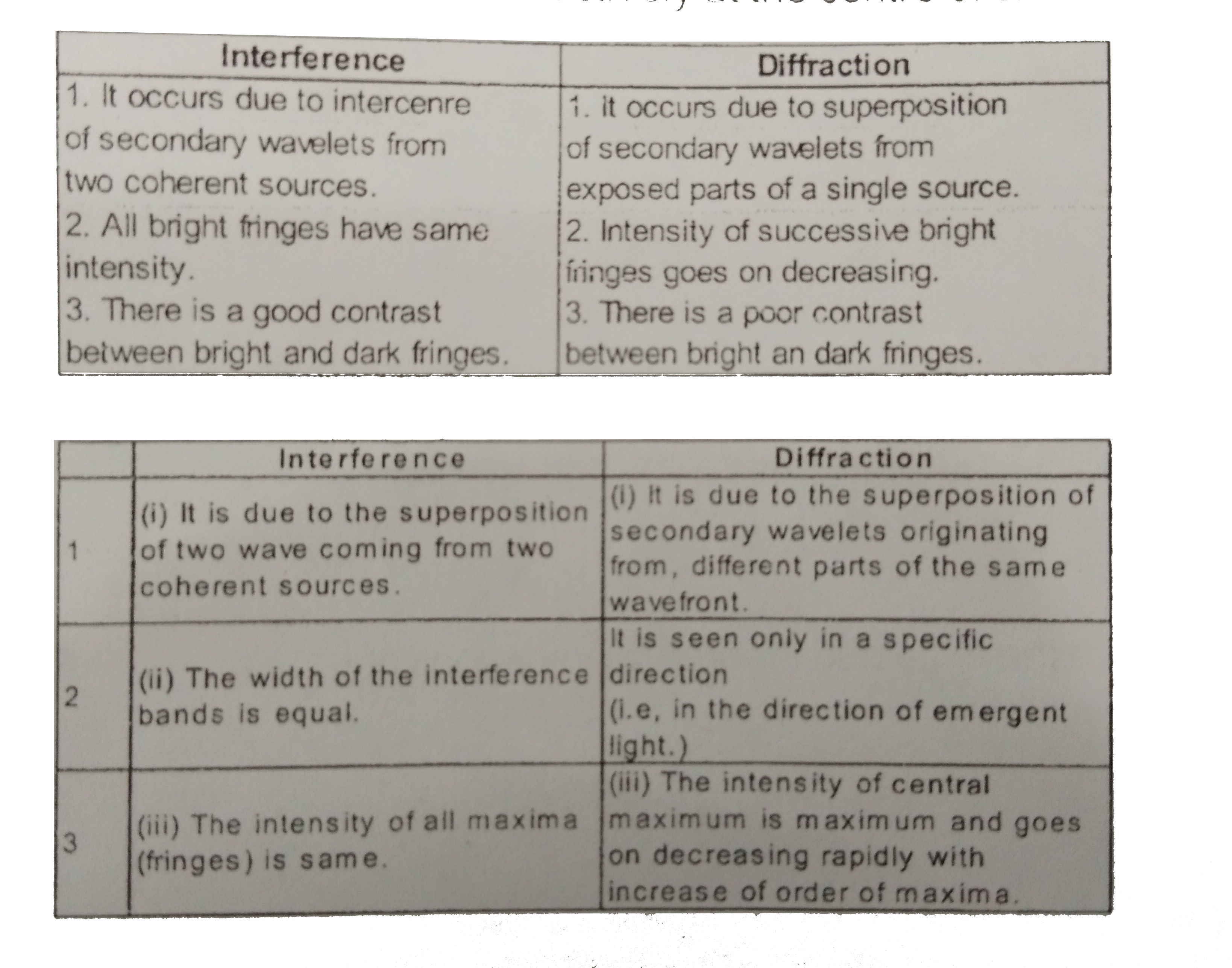
|
|
| 41322. |
The radius of a sphere is measured as (10 pm 0.02%) cm. The error in the measurement of its volume is |
|
Answer» 25.1 CC |
|
| 41323. |
An LR circuit having a time constant of 50 ms is connected with an ideal battery of emf epsilon . Find the time taken for the magnetic energy stored in the circuti to change from one fourth of the steady state value to half of the steady stae value. |
|
Answer» Solution :`t=(L/R)=50ms=0.05s` (a) `(i_0)/2=(i_0)(1-e^(-t//0.03))` `implies (1/2)=1-e^(-t//0.03)` `implies e^(-t//0.03)=(1/2)` `implies In e^(-t//0.03)=In(1/4)` (take In both sides) `impliest=0.05xx0.693` `=0.03465s` `=34.6ms=35ms` `(B) P=i^(2)R=(E^2)/(R)(1-e^(tR//L))^2` `Maximum POWER =(E^2)/(R)` so, (E^2)/(2R)=(E^2)/(R)(1-e^(tr/L)^2)` `implies1-e^(-R//L)=(1)/(sqrt(2))=0.707` `e^(-R//L)=0.293` `implies t=50xx1.2275ms` `=61.2ms` . |
|
| 41324. |
A current carrying circular coil of radius 11 cm is placed with its plane in magnetic meridian. The resultant magnetic induction at the centre of the coil is (Given current in the coil is 7A and B_(H)= 0.4 Gauss ] |
| Answer» Answer :C | |
| 41325. |
Which properties are independent of each other for waves propagating in the medium ? |
|
Answer» Velocity |
|
| 41326. |
An alpha -particle of energy 5 MeV is scattered through 180^@ by gold nucleus. The distance of closest approach is of the order of: |
|
Answer» `10^(-12)cm` `r_(0)=(1)/(4pi espi_(0)). (2Ze^(2))/(1/2 mu^(2))` `=(9 xx 10^(9) xx 2 xx 79 xx (1.6 xx 10^(-19))^(2))/(5 xx 1.6 xx 10^(-13))` `=(9 xx 2 xx 1.6 xx 1.6 xx 10^(-16) xx 79)/(5 xx 1.6)` `=455 xx 10^(-16)m` `=4.55 xx 10^(-12)cm` |
|
| 41327. |
A technician wraps wire around a tube of length 4pi^2 cm having a diameter of 8.00cm. When the windings are evenly spread over the full length of the tube, the result is a solenoid containing 1000turns of wire. If the current in this solonoid increases at the rate of 4.00A/s the self-induced emf in the solenoid is |
|
Answer» 32mV |
|
| 41328. |
The structural formula of the ore called natural magnet is |
|
Answer» `FeO_2` |
|
| 41329. |
A technician wraps wire around a tube of length 4pi^2 cm having a diameter of 8.00cm. When the windings are evenly spread over the full length of the tube, the result is a solenoid containing 1000turns of wire. If the current in this solonoid increases at the rate of 4.00A/s. the inductance of this solenoid is |
|
Answer» 32mH |
|
| 41330. |
Figure 26-24 gives the electric potential V(x) along a copper wire carrying uniform current, from a point of higher potential V= 12.0 muV at x= 0 to a point of zero potential at x= 3.00 m. The wire has a 0 radius of 2.20 mm. What is x (m) the current in the wire?. |
|
Answer» |
|
| 41331. |
Identify the part of electromagnetic spectrum to which the following wavelngth belong. (i) 10^(1)m (ii) 10^(-12)m |
| Answer» SOLUTION :MICROWAVES and MICROWAVE wovens. | |
| 41332. |
S_(1) and S_(2) are two coherent sources of frequency f each.(theta _(1)=theta_(2)=0^(@)) V_(sound)=330m//s. (i) so that constructive interfence at 'p' (ii) so that destructive interfrece at 'p' |
|
Answer» Solution :For constructive interference `K Delta x =2npi` `(2pi)/(lambda)xx2=2npi` `lambda=(2)/(n) , V=lambdaf rArr V=(2)/(n)f` `f=(330)/(2)XXN` For DESTRUCTIVE interference `K Delta x=(2n+1)PI` `(2pi)/(lambda).2=(2n+1)pi` `(1)/(lambda)=((2n+1))/(4), f=(V)/(lambda)=(330xx(2n+1))/(4)` |
|
| 41333. |
Carbon, silicon and germanium have four valence electrons each. These are characterised by valence and conduction bands separated by energy band gap respectively equal to ( E _(g))_(c ) , ( E_(g))_(Si )and ( E_(g ))_(G e ).Which of the following statements is true ? (a) (E_(g))_(Si) lt ( E_(g))_(Ge ) lt ( E_(g))_(C ) (b) ( E_(g))_(C ) lt ( E_(g))_(Ge )gt (E_(g))_(Si) (c ) (E_(g))_(C ) gt ( E_(g))_(SI) gt ( E_(g))_(Ge ) (d) ( E_(g))_(C ) = ( E_(g))_(Si) = ( E_(g))_(Ge ) |
|
Answer» `(E_(g))_(s i) LT (E_(g) )_(GE) lt (E_(g))_C ` |
|
| 41334. |
Explain the use of a junction transistor as an oscillator. |
|
Answer» Solution :An L-C circuit can be USED to produce oscillations of desired frequency. It consists of a tank circuit consisting of inductor L and capacitor C connected in parallel. The frequency of the tank circuit is given by `v=(1)/(2pisqrt(LC))` Due to the resistance of inductive coil, there occurs a small but constant energy loss and oscillations thus PRODUCED are damped. To transmit speech or music, we require undamped electromagnetic waves called carrier waves.  To do so an L-C circuit is coupled with transistor in such a way that there is a proper feedback to the L-C circuit at the proper timings so that the energy of L-C circuit REMAINS the same throughout oscillaitons. When key K is pressed, the collector attains positive POTENTIAL due to which a weak collector current will start rising in `L_(1)`. The increasing magnetic flux is linked with `L_(1)` and hence with L. |
|
| 41335. |
.Douglas went down towards the bottom |
|
Answer» only once |
|
| 41336. |
The distance from the earth's surface at which the acceleration due to gravity equals to 1m/s^2 is about |
|
Answer» Solution :MASS of the earth `VxxP=4//3pir^3rho g=GM//R^2=G/R^2(4/3piR^3rho)=4//3piRGrho` THUS, `galpharho` since R S G are constant . If `RHO` is DOUBLED, then g'=2g=2xx98=19.6m//s^2` |
|
| 41337. |
(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface. |
| Answer» Solution :(a) See Q. 25 (or) (a) 2015, DELHI Board , Set-I | |
| 41338. |
An air-cored solenoid is of length 0.3 m, area of cross section 1.2 xx 10^(-3) m^(2) and has 2500 turns. A roand its central section, a coil of 350 turns is wound. The solenoid and the coil are electrically insulated from each other. Calculate the enfinduced in the coil if the initial current of 3 A in the solenoid is reversed in 0.25s. |
|
Answer» Solution :`M=(mu_(0)N_(1)N_(2)A_(2))/(l)` `=(4pi xx 10^(-7) xx 2500 xx 350 xx 1.2 xx 10^(-3))/(0.3)H=4.4 xx 10^(-3) H` `e=M(dI)/(dt)""e=4.4 xx 10^(-3) xx (3-(-3))/(0.25)V=0.1056V` `***` If TWO solenoids are of UNEQUAL length, then length of bigger SOLENOID is to be considered. |
|
| 41339. |
The emf of a storage batery is 90 V before charging and 100 V after charging. When charging began the current was 10 A. What is the current at the end of charging if the internal resistance of the storage battery during the whole process of charging may be taken as constant and equal to 2 ohms ? |
|
Answer» 5A |
|
| 41340. |
A photograph of the moon was taken with telescope. Later on, it was found that a housefly was sitting on the objective lens of the telescope. In photograph |
|
Answer» The image of housefly will be REDUCED |
|
| 41341. |
A current of 5A passes through a long wire. Find the position of the point where it produces a magnetic field of induction0.36xx10^(-4)(Wb)//m^2 [mu_@=4pixx10^(-7) (Wb)//Am] DATA:i=5A, B=0.36xx10^(-4)(Wb)//m^2 mu_@=4pixx10^(-7) (Wb)//A To find:r=? |
|
Answer» Solution :Magnetic field B NEAR an INFINITELY long conductor `B=mu_@/(4pi)XX(2i)/r` `r=mu_@/(4pi)xx(2i)/B` `r=10^(-7)xx(2xx5)/(0.36xx10^(-4))=0.0278m=2.78cm` |
|
| 41342. |
Two capacitors of 4pF and 6pF are connected in series and a potential difference of 5 kV is applied across the combination. They are then disconnected and reconnected in paralle. The potential difference across combination is : |
| Answer» ANSWER :C | |
| 41343. |
A parallel plate capacitor with air between the plates has a capacitance of 8pF (1 pF = 10^(-12)F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6 ? |
|
Answer» Solution :Here `C = 8 pF = (epsi_0A)/d` Now `d. = d/2` and space is filled with a SUBSTANCE having K = 6. HENCE, new capacitance `C.= (K epsi_0A)/(d.) = (6epsi_0A)/((d/2)) = 12 (epsi_0A)/d = 12 xx 8 pF-96 pF.` |
|
| 41344. |
A plane polarized light is incident perpendicularly on polaroid. Taking incident light as an axis polaroid is rotated with an angular speed pi rads^(-1). If light energy incident in 1s is 4 mJ. How much energy will emerge after one rotation ? |
|
Answer» Solution :`int_(0)^(T)cos^(2)omegatdt=(pi)/(omega)` Here, `I_(0)=4mJ=4xx10^(-3)J,omega=pi" rad "s^(-1)` `I=I_(0)cos^(2)omegat` `:.` ENERGY emerging during one rotation, `=int_(0)^(T)I_(0)cos^(2)omegatdt` `=(I_(0)pi)/(omega)` `=(4xx10^(-3)xxpi)/(pi)` `4xx10^(-3)J` |
|
| 41345. |
Mean value or d.c. value of a.c. is _____ times the peak value. |
| Answer» SOLUTION :`2I_0/pi` | |
| 41346. |
The wavelength of a resonat mercury line is lambda==253.65nm. The mean life time of mercury atoms in the state of resonance excition is tau=.15 mu s. Evaluate the ration of the Doppler line broadening to the the natural linewidth at a gas temperature T=300K |
|
Answer» Solution :A short lived state of mean life `T` has an uncertainity in ENERGY of `DeltaE~( ħ)/(T)` which is transmitted to the PHOTON it emits as natural broadening. Then `Delta omega_(nat)=(1)/(T)` so `Delta_(lambda)_(nat)=(lambda^(2))/(2pic tau)` The Dopper broadening on the other hand ARISES from the thermal motion of radiating atoms. The effect is non-relativistic and the maximum brodening can be written as `Delta(lambda_(Dop))/(lambda)=2 beta=(2v_(pr))/(c )` Thus `(Deltalambda_(Dopp))/(Delta lambda_(nat))=(4piv_(pr)tau)/(lambda)` substitution gives USING `v_(pr)=sqrt((2RT)/(M))= 157 m//s` `(Delta lambda_(Dopp))/(Delta lambda_(nat))~~1.2xx10^(3)` Note:- Our formula is an order of magnitude estimate. |
|
| 41347. |
Obtain the formulas angular width and linear width of central maximum. |
|
Answer» SOLUTION :Width of central maximum is the distance between the first minimum on either side of the central maximum. Suppose, width of slit a is very SMALL (in the order of mm) and the distance between slit and screen is D (in the order of meter). This is shown in figure.  For a minimum of one side of the central maximum on the screen `theta=(lamda)/(a)` where `theta` is half the width of angular width of central maximum. `:.` Angular width of central maximum `2theta=(2lamda)/(a)` `2theta=(arc(beta_(0)))/("RADIUS"(D))` `:.beta_(0)=Dxx2theta` `=(2Dlamda)/(a)""....(1)""[:.theta=(lamda)/(a)]` Angle of `(n+1)^(TH)` order minimum `beta_(0)` is width of linear central maximum. It is minimum distance between the central maximum distance. Linear width of secondary maximum : The angular width in .n. means the least angular difference in n and (n + 1). `:.` The angle of least angular in .n., `theta_(n)=(nlamda)/(a)` Angle of `(n+1)^(th)` order minimum `theta_(n+1)=((n+1)lamda)/(Q)` `:.` Angular width of `n^(th)` secondary maximum, `theta_(n+1)-theta_(n)=(n+1)(lamda)/(a)-(nlamda)/(a)` `=(lamda)/(a)` `:.` The linear widht of `n^(th)` secondary maximum =angular width `xx` D `beta=(lamda)/(a)xxD""......(2)` `:.(beta_(0))/(beta)=2""` [ `:.` Ratio of equation (1) and (2)] `:.beta_(0)=2beta` |
|
| 41348. |
The magnetic charge -2 Am and +2 Am are seprated by a distance of 15 cm. The magnetic moment is : |
|
Answer» 0.5 `Am^2` |
|
| 41349. |
A long straight wire carrying a current of 30 A is placed in an external uniform magnetic field of induction 4xx10^(-4) T. The magnetic field is acting parallel to the direction of current. The magnitude of the resultant magnetic induction in tesla at a point 2.0 cm away from the wire is (mu=4pixx10^(-7)Hm^(-1)) |
|
Answer» `10^(-4)` |
|
| 41350. |
What is the area of the plates of a 2 F parallel plate capacitor, given that the separation between the plates is 0.5 cm? [You will realise from your answer why ordinary capacitors are in the range of µF or less. However, electrolytic capacitors do have a much larger capacitance (0.1 F) because of very minute separation between the conductors.] |
| Answer» SOLUTION :1130 `KM^(2)` | |