Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 91101. |
(a) Can a copolyer be formed in both addition and condensation polymerization ? Explain. (b) Can a homopolymer be formed in both addition and condensation polymerization ? Explain. |
|
Answer» SOLUTION :(a) YES , copolmers can be formed both in addition and condensation , polymerization. For example , Buna-S is an addition copolymer of styrene and 1,3-butadiene while nylon -6, 6, bakelite and polymer are (b) Yes, HOMOPOLYMERS can be formed both in addition and condensation polymerization. For example, POLYTHENE, PVC, PMMA, PAN. neoprene , etc. are examples of addition homopolymers while nylon -6 is an example of condensation homopolymer. |
|
| 91102. |
(a) Calculate the volume occupied at STP by (i)16.0 g of oxygen (ii) 1.5 moles of oxygen and (iii) 6.022xx10^(23) molecules of carbon dioxide |
| Answer» SOLUTION :(i) 11.20 L (II) 33.60 L (III) 22.4 L | |
| 91103. |
Calculate the standard free energy change for the following reaction occurring in the galvanic cell at 298 K. 3Mg(s)+2Al^(3+)(aq)rarr3Mg^(2+)(aq)+2Al(s) Given : E_(Mg^(2+)//Mg)^@=-2.37V and E_(Al^(3+)//Al)=-1.66 V |
|
Answer» Solution :(a) `E_(cell)=E_R^@-E_L^@` `=-1.66+2.37` =0.71 V `Delta G^@=-nFE^@ cell` `=-3 times 96500 times 0.71` `=-41090 J Or -411.09 K J` (b) BATTERY cannot be reused. |
|
| 91104. |
(a) Calculate the spin only magnetic moment of Ti^(3+)ion (Atomic number of Ti = 22).(b) Cu^(2+)salt solutions are coloured : given reason. |
|
Answer» Solution :(a) p = 7n (n + 2) `L = yJl(l + 2)=y//3` In `Zn_(2+) `, there is no unpaired electrons, HENCE it does not undergo d-d transition. Hence it is colourless. |
|
| 91105. |
(a) Calculate the standard free energy change and maximum work obtainable for the reaction. Zn(s)+Cu^(2+)(aq)hArrCu(s)+Zn^(2+)(aq) [Given E_(Zn^(2+)//Zn)^(@)=-0.76V,E_(Cu^(2+)//Cu)^(@)=+0.34V,F=96500" C "mol^(-1)] (b) also calculate the equilibrium constant for the reaction. |
|
Answer» Solution :(a) The cell may be represented as `Zn(s)|Zn^(2+)(1M)||CU^(2+)(1M)|Cu(s)` `E_(cell)^(@)=E_(RHS)^(@)-E_(LHS)^(@)=0.34-(-0.76)=1.10`volt For the given cell reaction, n=2 `DeltaG^(@)=-nFE_(cell)^(@)=-2xx96500" C "mol^(-1)xx1.10V=-212,300CV" "mol^(-1)` Thus, the MAXIMUM work that can be obtained from the Daniell cell=212.3 kJ. (b) `DeltaG^(@)=-RT" LN "K_(c)=-2.303RT" LOG "K_(c)` `therefore-212300=-2.303xx8.314xx298xxlog" "K_(c)" or "logK_(c)=(212300)/(2.303xx8.314xx298)=37.2074` `thereforeK_(c)="Antilog "37.2074=1.6xx10^(37)` |
|
| 91106. |
(a) Calculate the pressure exerted by 10^(23) gas molecules, each of mass 10^(-25) kg in a container of volume 1xx10^(-3) m^(3) and having root mean square velocity of 10^(3) ms^(-1) (b) Also, calculate total kinetic energy and (c ) temperature of the gas (b) What would be the final pressure of O_(2) in following experiment ? A collapsed polethylene bag of 30 litre capacity is partially blown up by the addition of 10 litres of N_(2) at 0.965 atm at 298 K, Subsequently enough O_(2) is pumped into bag so that at 298 K and exetrnal pressure of 0.990 atm, the bag contains 30 litre N_(2). |
|
Answer» Solution :(a) `P=(1 mNu^(2))/(3V) =(1xx10^(-25)xx10^(23) xx(10^(3))^(2))/(3xx10^(-3))` `=3.33xx10^(6) N m^(-2)` (b) Total `KE=((1)/(2) mu^(2))xx N` `=(1)/(2)xx10^(-25)xx(10^(3))^(2)xx10^(23)` `=(1)/(2)xx10^(4)` `=0.5xx10^(4)` Joule (c ) Also total kinetic energy 3/2 nRT `0.5xx10^(4)=(3)/(2)xx(10^(23))/(6.023xx10^(23))xx8.314xxT` `T=(0.5xx10^(4)xx2xx6.023)/(3xx8.314)` `=2415 K` (b) Given pressure of `N_(2)=0.965` atm Volume of `N_(2)=10` litre. Temperature of `N_(2)=298 K` `therefore` For `N_(2)` when bag is fully expanded. Volume of `N_(2)` (alone) =30 litre at 298 K `because P_(1) V_(1) =P_(2)V_(2)` `0.965xx10=P_(2)xx30 therefore P_(N_(2))` (alone) in 30 litre bag at 298 K =0.322 atm Now `P_(M)=P_(O_(2))+P_(N_(1))` `0.990 =P_(O_(z))+0.332` `therefore P_(O_(z))=0.668` atm |
|
| 91107. |
(a) Calculate the packing efficiency in hexagonal close packing arrangement. (b) Mention one consequence of metal excess defect. |
Answer» Solution :(a) 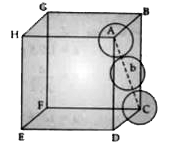 Packing Efficiency in hcp arrangement. In `Delta ABC" "AC^(2) = b^(2) = BC^(2) + AB^(2)` `b^(2) = a^(2) + a^(2) = 2a^(2) or b = sqrt(2) a` If r is the radius of the sphere, then b = 4r = `sqrt(2)` a or `a = 2 sqrt(2)r` Each UNIT cell in hcp has effectively 4 spheres. Total volume of four sphere is EQUAL to `4 xx ((4)/(3)) pi r^(3)` and volume of the cube is `a^(3) or (2 sqrt(2) r)^(3)` Packing efficiency `= ("Volume OCCUPIED by four spheres in the unit cell" xx 100)/("Total volume of the unit cell")` `= (4 xx (4)/(3) pi r^(3) xx 100)/((2 sqrt(2) r)^(3)) % = 74%` (b) It imparts colour to the crystal. |
|
| 91108. |
a) Calculate the packing efficiency of particles in a body centred cube. |
|
Answer» Solution :The number of atoms per unit cell in bcc structure is two. Each atom is considered as one sphere. Let the edge length of the unit cell = a Radius of the sphere = r Length of the body diagonal = c Length of the body diagonal = B In `DeltaEFD` `FD^(2)=EF^(2)+DE^(2)` `b^(2)=a^(2)+a^(2)=2a^(2)` Now in `DeltaAFD` `AF^(2)=AD^(2)+FD^(2)` Now in `DeltaAFD` `AF^(2)=AD^(2)+FD^(2)` `c^(2)=a^(2)+b^(2)` `c^(2)=a^(2)+2a^(2)=3a^(2)` `c =sqrt3a` `W.K.T c=4r` Therefore `=4r=sqrt3a` `a=(4r)/(SQRT3)`  `"Total volume of the unit cell "= a^(3) = ((4r)/(sqrt3))^(3)` Since bcc LATTICE contains 2 atoms per unit cell `"Volume of two spheres "=2 xx(4)/(3)pir^(3)` `"Packing efficiency "= ("Volume of the two spheres in unit cell")/("Total volume of the unit cell")xx100%` `=(2xx(4)/(3)pir^(3))/(((4r)/(sqrt3))^(3))xx100%` `=((8)/(3)pir^(3))/((64)/(3SQRT3)r^(3))xx100=68%` |
|
| 91109. |
Calcium metal crystallises in a face centered cubic lattice with edge length of0.556nm. Calculate the density of the metal. [Atomic mass of calcium 40 g/mol] [N_(A) = 6.022 xx 10^(23) " atoms/ mol"] |
|
Answer» Solution :(a) Let a be the uit cell edge length and be the face diagonal In `Delta ABC, ""AC^(2) = BC^(2) + AB^(2)` `b^(2) = a^(2) + a^(2) = 2a^(2)` `b = sqrt(2)a` if r is the radius of the sphere, we find `b = 4r = sqrt(2)a` or `a = (4r)/(sqrt(2)) = 2sqrt(2)r` f.c.c. structure has 4 spheres per unit cell and their volume is `4 xx (4)/(3) pi r^(3)` and the volume of the cube is `a^(3)` or `(2sqrt(2)r)^(3)` Therefore, Packing EFFICIENCY `= ("Volume occupied by four spheres in the unit cell")/("Total volume of the unit cell") xx 20` `= (4 xx (4)/(3)pi r^(3))/((2sqrt(2)r)^(3)) xx 100% = ((16)/(3) pi r^(3))/(16sqrt(2)r^(3)) xx 100% = 74%` (b) `d = (z xx M)/(a^(3) xx N_(A))` `d = (4 xx 40)/((0.555 xx 10^(-7))^(2)(6.022 xx 10^(23)))` `= 1.545 g//cm^(3)` or `1.545 xx 10^(3) kg//m^(3)`. |
|
| 91110. |
(a) Calculate the number of particles in Face Centred Cubic (FCC) lattice.(b) What is Frenkel defect? What is its effect on the density of a solid? |
|
Answer» Solution :(a) LET .a. : be the edge length of the cube ’b. : be the face diagonal ’r’: is the radius of the sphere b= 4r In `Delta` ABC `b^(2) = a^(2) + a^(2)` `b^(2) = 2a^(2)` `b = sqrt(2)xx a `4r= sqrt(2)xx a, a =`4/sqrt(2)r`,a=`2sqrt(2)r` • Volume of the cube = `a^(3) =(2sqrt(2)r)^(3)` • Each unit CELL of CCP structure contain 4 SPHERES. • Volume of the four spheres = `4xx4/3(PIR^(2)` • Packing efficiency = Volume of 4 atoms in the unit cell/( Total volume of the unit cell )`xx100` `=(4xx4/(3)pir^3()/(2sqrt(2)r)^(3)xx100 ` Packing efficiency= 74%. 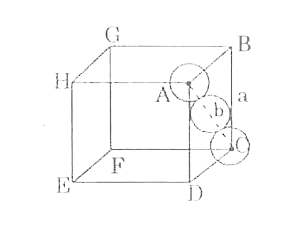
|
|
| 91111. |
(a) Calculate the packing efficiency in c ccp crystal lattice. (b) What is the number of particles per unit cell of a simple cube. |
|
Answer» Solution :(a) Let a is the edge length of the cube, Each UNIT cell in hcp (or) CCP has effectively 4 spheres. Total volume of fous sphere is equal to `4 XX (4)/(3) pi r^(3)` and volume of the cube is `a^(3) or (2 sqrt(2) ar)^(3)` Packing EFFICIENCY of ccp `= ("Volume occupied by 4 spheres in the unit cell")/("Total volume of the unit cell" (a^(3)))` `= (4 xx (4)/(3) pi r^(3) xx 100)/((2 sqrt(2) r)^(3)) = 74%` (b) 1 or one. |
|
| 91112. |
(a) Calculate number of particles in Face Centred Cubic (FCC) structure. (b) Write any two differences between Frenkel and Schottky defects. |
|
Answer» Solution :(a)Let a be the edge length of the cube ‘A’ : be the face diagonal ‘R’ : is the radius of the sphere b = 4r • In A ABC `b^(2) = a^(2) + a^(2)` `b^(2) = 2a^(2)` `b = a sqrt(2) xx a` `4r =sqrt(2) xx a` ` a =4/(sqrt(2)) implies a =(2A)//(2t)` • Volume of the cube = `a^(3) = ^2-j2r j` • Each unit cell of CCP structure contain 4 spheres. • Volume of the four spheres = 4 x — it `4/8 r^(3)` Packing efficiency =`("Volume of 4 ATOMS in the unit cel"L)/(T"otal volume of the unit cel"l)` `=(Z4x^(4)-NR^(3))/(2V2r) xx100` Packing efficiency = 74%. (b) Ionic solids showing Schottky defect -NaCl, KCl, CsCl, AgBr. Ionic solids showing Frenkel defect – ZnS, AgCl, AgBrAgl. 
|
|
| 91113. |
Calculate the number of paricles per unit cell of FCC . |
|
Answer» Solution :In `Delta ABG_3` `b^2= a^(2) +a^(2)`therefore `b^(2) = 2a^(2)`, In, `Delta AGD`, `C^(2) = a^(2)+b^(2)` = `a^(2) + 2a^(2)`therefore`C= sqrt(3A)` Radius of the atom =r Length of thee body diagonal `C= 4r` `sqrt3a `= `4r`,a= `(4r)/sqrt3` Edge length of the cube = a = `(4r)/sqrt3` volumeof the cubic UNIT cell. = `a^3 =((4r)/sqrt3)` Volume of one particle (sphere ) = `4/3pir^(3)` The number of particle per unit cell of a BCC=2 The volume occupied by two spheres = `2xx4/3 pir^(3)` packing efficiency = `("TOTAL volume occupied by the two spheres")/ ("volume of a cubic unit cell" ) xx100` `(4/3pir^3xx2)/(4/sqrt3r)^3xx100 = (8/3pi r^3)/((64)/((3)sqrt3) r^3 )xx100= 68%` (1) A face centerd cube contains 8 lattice points at theeight coner and 6 lattice point at the center of six faces. (2) A particle present at the centre of a face provides a share of 1/2 of that particle to each unit cell . (3) A particle present at the centre of a face provides a shareof 1/2 of that particle to each unit cell . (4) The number of particles presemnt in unit cell of fee = `1/8xx 8+ 1/2 xx6= 1+3 =4`. |
|
| 91114. |
(a) Calculate the packing efficiency in body centered cubic lattice. (b) What is Schottky defect? |
|
Answer» Solution :(a) In `Delta ABC` `b^(2) = a^(2) + a^(2):. b^(2) = 2a^(2)`, In `Delta AGD` `C^(2) = a^(2) + b^(2) = a^(2) + 2a^(2):. C = sqrt(3)a` RADIUS of the atom = r Length of the body DIAGONAL C = 4r `sqrt(3)a = 4r,a = 4r/sqrt(3)` Edge length of the CUBE = `a = 4r/sqrt(3)` Volume of the cubic unit cell = `a^(3) = (4r/sqrt(3))^(3)` Volume of one particle per unit cell of a BCC = 2 Total volume occupied by two spheres = ` 2 xx 4/3 pir^(3)` Packing Efficiency = ` (4/3 pir^(3) xx 2)/(4/sqrt(3)r)^(3) xx 100 = (8/3 pir^(3))/(64/3sqrt(3)r^(3)) xx 100 = 68%` (b)When equal number of cations and anions are missing from their lattice.sites, the DEFECT is called Schottky defect. |
|
| 91115. |
(a) Calculate the number of particles in BCC lattice.(b) Calculate the number of particles per unit cell in FCC. |
|
Answer» Solution :(a) The number of atoms per unit CELL in bcc structures is two. Each atom is considered as one sphere. So, the volume of two atoms (two spheres) =? `2xx4/3pir^(3)` From the figure it is clear that there are three spheres touching each other along the L. diagonal. Let a be the edge length of the cube and r be the radius of the sphere. The diagonal AF = c and face diagonal FD = b , then AF - c = 4r. In AEFD `FD^(2)= EF^(2) + ED^(2)` `b^(2) – a^(2) + a^(2) = 2a^(2)` `b = V2a ` In `Delta AFD` `AF^(2)=AD^(2)+FD^(2)c^(2)=a^(2)+b^(2)=a^(2)+2a^(2)=3a^(2)`. `c= sqrt(3)a` but c=4r therefore `sqrt(3)a=4r` a`=(4r)/sqrt(3)` volume of unit cell=`a^(3)=((4r)/sqrt(3))^(3)` Therefore Packing efficiency = `("Volume of two atoms (two spheres) in unit cell")/("Volume of the unit cell")xx100` Packing efficiency `= (8/3pir^(3))/(64/(3sqrt(3))r^(3))xx100% =sqrt(3) pi XX 100= 68%` Therefore 68% of unit cell is occupied by atoms and the rest 32% is empty space in bcc structures. The packing fraction in bcc structures = 0.68 The fraction of empty space in bcc structures = 0.32. (b) Number of particles per unit cell of FCC = `(1)/(82)`(No. of comer particles) + `(1)/(82)`(No. of facial particle) = `1/8 +1/6 = l + 3=4` 
|
|
| 91116. |
(a) Calculate the packing efficiency in a Face Centered Cubic lattice. (b) If a metal with atomic mass 209 crystallizes in a simple cubic lattice what is the edge length of its unit cell. (Given d = 91.5 kg m-3). |
|
Answer» Solution : (a) The number of atoms per unit cell in fcc structures is four. Each ATOM is considered as one sphere. So, the volume of four atoms (four spheres) - `4xx 4/3 pi r^(3) =16/3 pi r^(3)` From this FIGURE it is clear that there are three spheres touching each other ALONG the face diagonal. Let .a. be the edge length of the cube and .r. be the radius of the sphere. The face diagonal AC = b, then b = 4r. In ABC, `AC^(2) = BC^(2) + AB^(2)` `b^(2)= a^(2)+ a^(2)` ` b^(2)= 2a^(2)` `b= sqrt(2a)= 4r`` b= sqrt(2a) =4r` ` a= 4r/sqrt(2) =2sqrt(2r)` the volume of the cubic unit cell = `a_(3) = (2sqrt(2r)^(3)` therefore, packing efficiency=volume of four atoms(four spheres) in unit cell/ volume of unit cell `xx100 % ` packing efficiency =` (16/3pir^(3))/((2sqrt(2r)^(3)))xx100%` packing efficiency`=(16/3 xx22/7 r^(3))/(8(sqrt(2))^(3) r^(3)) xx100% ` packing efficiency = `(16/3xx22/7)/(8(sqrt2)^(3))xx100% =74%` therefore 74% of unit cell is occupied by atoms and the rest 26% is empty space in fcc structure . the packing fractionin fcc structure (ccp)= 0.74 the fraction the fraction of fraction of empty space in fcc structure (ccp)0.26 (b) `a^(3)= (ZM)/(N_(A)d)= (1xx209)/(6.023xx10^(23)xx91.5xx10^(-3))`, `a^(3)= 3.359xx10^(-6) cm`. 
|
|
| 91117. |
Calculate the packing efficiency in a simple cubic lattice. |
|
Answer» Solution :In a simple cubic lattice, the atoms are LOCATED only on the CORNERS of the cube. The NUMBER of atoms per unit cell in simple cube is one. Each atom is considered as one sphere. Let the edge length of the cube be `= a` The radius of each atom `= r` `a=2R`  Total volume of unit cell `=a^(3)=(2r)^(3)=8r^(3)` So, the volume of one atom (one sphere) `=(4)/(3)pi^(3)` `"Packing efficiency "=("Volume of one sphere (atom)")/("Total volume of the unit cell")xx100%` `"Packing efficiency "=((4)/(3)pir^(3))/(8r^(3))xx100=(pi)/(6)xx100=52.4%` |
|
| 91118. |
a. Calculate the packing efficiency in a Body Centered Cubic (BCC) lattice. b. Silver forms a ccp lattice. The edge length of its unit cell is 408.6 pm. Calculate the density of silver. (N_(A)=6.022xx10^(23)," Atomic mass of Ag "=108 g mol^(-1)) |
Answer» Solution : LET .a. be the edge length of unit cell .R. be the radius of each particle From `hat(EFD):b^(2)=a^(2)+a^(2)=2a^(2)` From `hat(AFD),c^(2)=b^(2)+a^(2)` `=2a^(2)+a^(2)rArr 3a^(2)` `c=4r` `4r=sqrt3a` `a=(4r)/(sqrt3)` `"Volume of cubic unit cell "=a^(3)=((4r)/(sqrt3))^(3)` `"Number of PARTICLES PER BCC unit cell"=2` `"Packing efficiency"=("Volume occupied by 2 particles "xx100)/("Volume of unit cell")=(2xx4pir^(3))/(3xx((4r)/(sqrt3))^(3))xx100=68%` b. Given : a = 408.6 pm `d=?` `M=108gmol^(-1)z=4` `N_(A)=6.022xx10^(23)` `d=(zm)/(a^(3).NA)=(4xx108)/((408.6)^(3)xx6.022xx10^(23)xx10^(-30))` `d=10.5gcm^(-1)` |
|
| 91119. |
(a) Calculate the number of unit cell in 8.1g of aluminium if it crystallises in a fcc structure. (Atomic mass of Al = 27g*mol^(-1)) (b) Give reasons: (i) In stoichiometric defects, NaCl exhibits Schottky defect and not Frenkel defect. (ii) Silicon on doping with Phosphorous forms n-type semiconductor. (iii) Ferrimagnetic substances show better magnetism than anti-ferromagnetic substances. |
|
Answer» Solution :(a) NUMBER of aluminium atoms present in 8.1 g of `Al=(8.1xx6.022xx10^(23))/27` In fcc structure, each unit cell consists of 4 Al atoms as Al crystallises in fcc structure. Therefore, number of unit cell in 8.1 g of Al `=(8.1xx6.022xx10^(23))/(27xx4)=4.5165xx10^(22)` (b) In ferrimagnetic substances, in PRESENCE of magnetic FIELD domains are aligned in opposite direction in UNEQUAL number and hence they have some NET magnetic momnet. On the other hand, in anti-ferromagnetic substances, in presence of magnetic field the domains are aligned in opposite direction in equal number. So they cancel magnetic moment completely and hence zero magnetic moment. 
|
|
| 91120. |
(a) Calculate the osmotic pressure of 0.05% urea solution in water at 20°C.Given R = 0.0821 Latm mol^(-1) K^(-1), Molar mass of urea = 60 g mol^(-1).(b) Give two general characteristics of an ideal solution of two liquids. |
|
Answer» Solution :(a) `PI = W_(2)RT/M_(2)V = xx 0.0821 xx 293/60 xx`(b) 1. Obey Raoult.s Law 2. `DELTAH` of mixing is zero. |
|
| 91121. |
(a) Calculate the number of atoms per unit cell of fcc. (b) What is ferromagnetism ? Give an example for ferromagnetic substance. (c) Give an example for molecular solid. |
|
Answer» Solution :(a) 8 corner atoms `xx (1)/(8)` ATOM + 6 face centered atoms `xx (1)/(2)` atom = 4. (B) SUBSTANCES which are strongly attracted by magnetic field. Iron or Cobalt or Nickel or `CrO_(2)` or any other. (c) `I_(2)` or any SUITABLE example. |
|
| 91122. |
(a) Calculate the mass of Ag deposited at cathode when a current of 2 amperes was passed through a solution of AgNO_3 for 15 minutes. [Given : Molar mass of Ag = 108 g mol^(-1), 1 F = 96500 C mol^(-1)] (b) Define fuel cell. |
|
Answer» SOLUTION :(a) Here, `t = 15 xx 60 =900` seconds, current =2 amperes `therefore` Charge = Current `xx` time `=2 xx 900 = 1800 C` `Ag^(+) + e^(-) to Ag(s)` We require 1F or 96500 C to deposit ONE mole or 108 g of Ag. Mass deposited with 1800 C `=108/96500 xx 1800 g = 2.0145 g` (6) Fuel cell : Galvanic cells that are designed to convert the energy of combustion of fuels like HYDROGEN, methane, methanol, etc., directly into electrical energy are CALLED fuel cells. |
|
| 91123. |
(a) Calculate the equilibrium constant for the reaction : Cd^(2+) (aq) + Zn(s) |
|
Answer» Solution :(a) `E_("cell")^(@) = E_(Cd^(2+)//Cd)^(@) -E_(Zn^(2+)//Zn)^(@) = -0.403 V - (-0.763 V) = + 0.36 V` `nFE^(@) =2.303 RT ln K` or `log K = (nFE^(@))/(2.303 RT) =(nE^(@))/((2.303 Rt)/F) =(2 xx 0.36)/0.0591 = 12.2033` or `K = 1.5969 xx 10^(12)` (b) By FARADAY.s law. Quantity of electricity = 25 x 60 x 0.75 coulombs = 1125 C = 0.01166 Faraday 0.01166 Faraday of charge deposits = 0.369 G of copper. 2 Faraday of charge deposits `=0.369/0.1166 xx 2g` of copper = 63.3 g At. mass of copper = 63.3 u ( c) We want to see if the reaction: `Ag_(2)S (s) + Zn to 2Ag(s) + ZnS` can take place `E_("cell") = E_(Ag_(2)S//Ag)^(@) -E_(Al^(3+)//Al)^(@)` `=-0.71 -(-1.66)` `=+0.95 V` As the cell emf is POSITIVE, the reaction will take place i.e., tarnish can.be removed. |
|
| 91124. |
(a) Calculate the equilibrium constant for the following reaction at 25^@C.Sn(s) + Pb^(2+)(aq) to Sn^(2+) (aq) + Pb(s)The standard emf of the corresponding voltaic cell is 0.01 V.(b) If an excess of tin metal is added to 1.0 M Pb^(2+), what is the concentration of Pb^(2+)at equilibrium? |
| Answer» SOLUTION :(a) 2.2 (B) 0.3 M | |
| 91125. |
a) Calculate the e.m.f. of the cell represented below: Ni_((s))|Ni_(0.1M)^(2+)||Ag_(0.01M)^(+)|Ag_((s))" at 298Given,"E_("cell")^(@)=1.05V, |
|
Answer» SOLUTION :Cell REPRESENTATION `Ni|Ni^(2+)||Ag^(+)|Ag` Applying nernst EQUATION, `E_("cell")=E_("cell")^(@)-(0.0591)/(n)LOG""([Ni^(2+)])/([Ag^(+)]^(2))` `=1.05-0.02955 log=(0.1)/((0.01)^(2))` `=1.05-0.02955log=(0.1)/((0.01)^(2))` `=1.05-0.02955log""(0.1)/(0.0001)` `=10.5-0.02955 log100` `=1.05-0.02955log10^(2)rArr 2LOG10` `=1.05-0.02955[2log10]` `=1.05-0.059rArr 0.459V` |
|
| 91126. |
(a) Calculate the emf of the cell in which the following reaction takes place Ni(S) + 2Ag^(+)(0.002M) rarr Ni^(2+)(0.160M) + 2Ag(S) Given that E_(cell)^(circ)= 1.05V (b) A galvanic cell after use is recharged by passing current through it. What type of cell is it? Give an example. |
|
Answer» Solution :(a) Applying Nernst Equation, `E_(CELL) = E^(circ)_(cell) - 0.0591/n log[Ni^(2+)]/[Ag^(+)]^(2)` `= 1.05 - 0.02955 log (0.160)/(0.002)^(2) = 1.05 - 0.02955log(0.16)/(0.002)^(2)` `= 1.05 - 0.02955log 4 xx 10^(4) = 1.05 - 0.02955(log10000 + log 4)` `= 1.05 - 0.02955(4 +0.6021) = 0.914V` (b) Secondary cell e.g. Lead storage BATTERY |
|
| 91127. |
(a) Calculate the emf for the given cell at 25^@C: Cr|Cr^(3+) (0.1M)||Fe^(2+) (0.01M) |Fe (b) calculate the strength of the current required to deposit 1.2g of magnesium from molten MgCl_2 in 1 hour. |
|
Answer» Solution :`E.M.E=E_(cell)^@-0.059/n log""(Products)/(Reactants)` `Cr|Cr^(3+) (0.1M)||Fe^(2+) (0.01M)|Fe` Equation, `2Cr+3Fe^(2+)to 2Cr^(3+)+3Fe` `E_(Cr^(3+)//Cr)^@=-0.74E_(Fe^(2+)//Fe)^@=-0.44V` `E_(cell)^@=E_(cathode)-E_(ANODE)` `=-0.44-(-0.74)` =0.3 `E_(cell)=0.3-0.059/n log""(0.1)^2/(0.01)^3` `=0.3-0.0098 log""0.01/0.00001` `=0.3-0.0098 log 10^4` `=0.3-0.0393` `=+0.260 V` (b) The half reaction occuring during deposition is: `Mg^(2+)+2e^(-) to Mg(s)` So to produce 1 mole of Mg we need 2 moles of ELECTRONS, 1 mol of Mg=24 G Thus 1.2g of Mg=(`1.2//24`)=0.05 moles Hence no. of moles of electrons REQUIRED to deposit `=0.05 TIMES 2=0.1 mol es` Hence no. of moles of electrons required to deposit `=0.05 times 2=0.1 mol es` Qty. of electricity passed (Q)= moles of electrons `passed times 96500` `=0.1 times 96500=9650 C` `I=Q//t` `I=9650/(60 times 60(converti ng 1 hr into seconds))` `I=9650/3600=2.68A` |
|
| 91128. |
a.Calculate the depression in freezing point (Delta T_(f)) of 0.1 m solution of ROH in cold conc. H_(2)SO_(4) . K_(f) = x K kg mol^(-1) b.Calculate the Delta T_(1) of 0.2 m solution of Ph_(3) C--OH in cold conc.H_(2)SO_(4) . K_(f) = x K kg mol^(-1) . |
|
Answer» Solution :a.ROH reacts with cold cons. `H_(2)SO_(4)` as follows: 1.`ROH + H_(2)SO_(4) rarr RO^(o+)H_(2) + HSO_(4)^(-) rarr ROSO_(2)OH` + `cancel (H_(2)O)` 2.`{:(H_(2)SO_(4)+cancel(H_(2)O)toH_(3)O^(o+)+HSO_(4)^(-)),(ulbar(ROH+2H+2H_(2)SO_(4)toROSO_(2)OH+H_(3)O^(o+)+HSO_(4)^(-))):} Number of moles of particles formed per mole of solute (i) (van't Hoff factor) = 3 (The reaction does not produce `R^(o+)`, because `R^(o+)` ion or even `R_(3)C^(o+)` ion is not stable enogh to PERSIST. `:. Delta T_(f) = i K_(f)xxM` `= 3x xx 0.1 = 0.3x K` b.`Ph_(3)C---OH` reacts with cold conc.`H_(2)SO_(4)` as follows: 1.`Ph_(3)COH + H_(2)SO_(4) rarr Ph_(3)C^(o+)` + `cancel (H_(2)O)` + `HSO_(4)^(-)` 2.`{:(H_(2)SO_(4)+cancel(H_(2)O)toH_(3)O^(o+)+HSO_(4)^(-)),(ulbar(Ph_(3)COH+2H+2H_(2)SO_(4)toPh_(3)C^(o+)+H_(3)O^(o+)+2HSO_(4)^(-))):} Number of moles of particles formed per mole of solute (i) (Van't Hoff factor) = 4 (The reaction PRODUCES stable `Ph_(3)C^(o+)` ion due to resonance stabilisation, and `Ph_(3)C^(o+)` PERSISTS in the solution.) `:. Delta T_(f) = i K_(f)xxM` `= 4x xx 0.2 = 0.8x K`. |
|
| 91129. |
(a) Calculate the electrode potential of silver electrode dipped in 0.1 M solution of silver nitrate of 298 K assuming AgNO_(3) to be completely dissociated. The standard electrode potential of Ag^(+)|Ag is 0.80V at 298K. (b) At what concentration of Ag^(+) ions will this electrode have a potential of 0.0 volt? |
|
Answer» (b) `E_(Ag^(+)//Ag)=0therefore0=0.80-(0.0591)/(1)"log"(1)/([Ag^(+)])` or `log[Ag^(+)]=-(0.80)/(0.0591)=-13.5364=overline(14).4636` or `[Ag^(+)]=2.9xx10^(-14)M` |
|
| 91130. |
(a) Calculate the degree of dissociation 'A' and 'B' are dilute . The limiting molar conductivity of 'B' increases to a smaller extent while that 'A' increase to a much larger extent comparatively . Which of the two is a strong electrolyte ? Justify your answer . (b) Solution of two electrolytes 'A' and 'B' are dilute . The limiting molar conductivity of 'B' increases to a smaller extent while that of 'A' increase to a much larger comparatively . Which of the two is a strong electrolyte ? justify your answere. |
|
Answer» Solution : According ti KOHLRAUSCH law `Lamda^(@)(CH_(3)COOH)= lamda_(H+)^(@)+lamda_(CH_(3)COO^(-))^(@)` `= 349.6+40.9=390Scm^(2)mol^(-1)` `Lamda_(m)= (Kxx1000)/(c )` `Lamda_(m)= (8.0xx10^(-5)Scm^(-1)xx1000cm^(3)L^(-1))/(0.0024molL^(-1)) = 33.33Scm^(2)mol^(-1)` `alpha=(Lamda_(m))/(Lamda_(m)^(@)` `alpha=(33.33Scm^(2)mol^(-1)/(390.5Scm^(2)mol^(-1)`= 0.085 Electrolyte B is a STRONG electrolyte . Limiting molar cinductivity increases only to a smaller extent for a strong , as on dilution the interaction are overcome . The degree if dissociation increases , therefore the number of ions in total volume of solution increases. |
|
| 91131. |
a) Calculate the charge in coulombs required for the oxidation of 2 moles of water to oxygen ? [Given 1 F = 96500 C mol^(-1) ] (b) Zinc/Silver oxide cell is used in hearing aids and watches. The following reactions occur : Zn(s) to Zn^(2+)(aq) + 2e^(-), E_(Zn^(2+)//Zn)^(@) = -0.76 V Ag_(2)O + H_(2)O + 2e^(-) to 2Ag + OH^(-), E_(Ag^(+)//Ag)^(@) = 0.344 V Calculate (i) Standard potential of the cell, (ii) Gibb's free energy: |
|
Answer» Solution :(a) `2H_(2)O (l) to O_(2)(g) + 4H^(+) (aq) + 4e^(-)` Two molecules of water release four electrons for oxidation to oxygen. Thus four Faradays of electricity is required for the oxidation of two moles of water. Charge in coulombs = 4 x 96500 coulombs = 386000 coulombs (b)(i) Zinc electrode is the anode while silver electrode is the cathode: `E_("cell")^(@) = 0.344 V - (-0.76 V) = 1.104 V` ii) Gibbs free energy can be CALCULATED as under : `DeltaG^(@) = -NFE^(@)` Substituting the values, we have `DeltaG^(@) =-2 XX 9650 C MOL^(-1) xx 1.104 V` `=-213072J mol^(-1) = -213.072 kJ mol^(-1)` |
|
| 91132. |
(a) Calculate the charge in coulombs required for oxidation of 2 moles of water to oxygen ? [Given: 1F = 96,500 C mol^(-1)] (b) Zinc/silver oxide cell is used in hearing aids and electric watches. The following reactions occur : Zn(s) to Zn^(2+) (aq) + 2e^(-), E_(Zn^(2+)//Zn)^(@) =-0.76 V Ag_(2)O + H_(2)O + 2e^(-) to 2Ag + 2OH^(-), E_(Ag^(+)//Ag)^(@) = 0.344 V Calculate (i) standard potential of the cell, (ii) standard Gibbs energy. |
|
Answer» Solution :`2H_(2)O (l) to O_(2)(g) + 4H^(+) (aq) + 4e^(-)` 2 molecules of water release 4 electrons for OXIDATION to oxygen or 4 Faradays of electricity is required for the oxidation of 2 moles of water to oxygen. Charge in coulombs required for the process = 4 x 96500 coulombs = 386000 coulombs (b)(i) Zn electrode is the anode while silver electrode is the cathode. `E_("CELL")^(@) = E_("cathode") - E_("anode")` `=0.344 V - (-0.76 V) = 1.104 V` (ii) `DeltaG^(@) =-nFE_("cell")^(@)` n=2 (Because 2 electrons each are INVOLVED in the anode and cathode reactions) F = 96500 COLUMBS `E^(@) = 1.104 `V Substituting the values, we have `DeltaG^(@) =-2 xx 96500 xx 1.104 = -213072 J mol^(-1) = -213.072 kJ mol^(-1)`. |
|
| 91133. |
a) Calculate pH of 10^(-8) M H_2 SO_4 |
|
Answer» Solution :`underset(10^-8 M)(H_2 SO_4) OVERSET(H_2O)(hArr)underset(2XX10^(-8))(2H_3O^+)+underset(10^(-8)M)(SO_(4)^(2-))` In this case the concentration of `H_2SO_4` is very low and HENCE`[H_3O^+]` from water cannot be NEGLECTED `therefore [H_3O^]=2xx10^(-8)("from" H_2 SO_4)+10^(-7)` (from water) ` = 10^(-8)(2+10)` `=12xx10^(-8)=1.2xx10^(-7)` `pH=-log[H_3 O^+]` `=-log_(10)(1.2xx10^(-7))` `=7 -log_(10)1.2` `=7-0.0791=6.9209`. |
|
| 91134. |
An element having atomic mass 63.1 g/mol has face centered cubic unit cell with edge length 3.608 xx 10^(-8) cm. Calculate the density of unit cell [Given N_(A) = 6.022 xx 10^(23) atoms/mol]. |
|
Answer» Edge LENGTH or side of a cube =a, radius of a particle = r Particles TOUCH each other ALONG the edges . `therefore a=2r`,volume of cell =`a^(3)=8r^(3)`. A simple cubic unit cell contains only 1 atom. Volume occupied =`4/3pir^(3)` Packing efficiency `=`volume of one atom //volume of the unit cell `xx100 %` =`(4//3pi r^(3))/(8r^(3))"xx100=52.4%`  (b) `d=(Z.M)/(a^3.Na)`=`(4 atoms xx63.1 g//mol) //(3.608xx10^(-8)cm)^(3) xx(6.022 xx 10^(23)) `atom =`8.92 gcm^(-3)` |
|
| 91135. |
Calculate the e.m.f. of the cell in which the following reaction takes place. Ni_((s)) + 2Ag_((0.002M))^(+) to Ni_((0.160M))^(2+) + 2Ag_((s)) , "Given "E_("cell")^@ = 1.05 V |
|
Answer» Solution :(a) From the given cell reaction and Nernst equation `E_(cell) = E^(circ)_(cell) - 0.0591/n log[NI^(2+)]/[Ag^(+)]^(2)` `= 1.05V-0.0591/2 log[0.160]/[0.002]^(2)` `1.05-0.0591/2 log(4 xx 10^(4))` `1.05 - 0.0591/2 (4.6021)` `1.05 - 0.14 = 0.91 V` = `E_(cell) = 0.91 V` (b) The amount of substance deposited at an electrode is directly proportional to QUANTITY of current passed through its solution. MATHEMATICALLY, `WQ` `WIT` `W = ZIT` Where, W = mass, I = current in ampere, t = time in second, Z = electrochemical equivalent. |
|
| 91136. |
(a) Calculate /_\G_"f"^0 of the following reaction Ag^+(aq)+Cl^(-)(aq) rarr AgCl(s) given /_\G_"f"^0 (AgCl) = -109kJ//"mole", _"f"/_\G^0(Cl^-)=-129kJ//"mole" _"f"/_\G^0(Ag^+)=77kJ//"mole" represent the above reaction in from of a cell. Calculate E^0 of the cell. Find log_10K_(SP)of AgCl (b) 6.539xx10^-2 g of metallic Zn (amu = 65.39) was added to 100 ml of saturated solution of AgCl. Calculate log_10([[Zn^(2+)]]/[Ag^+]^2) ,given that Ag^++e^(-) rarr AgE^0=0.80V , Zn^(2+)+2e^(-) rarr ZnE^0=-0.76V Also find how many moles ofAg will be formed? |
|
Answer» |
|
| 91137. |
(a) calculate packing efficiency in simple cubic lattice. (b) An element having atomic mass 107.9 u has FCC lattice . The edge length of its unit cell is 408.6 pm calculate density of the unit cell.Given, NA=6.022xx10^23 mol-1]. |
|
Answer» SOLUTION :(B) `GIVEN, NA=6.002xx1023 mol-1` `(4xx107.9xx10^3)/((408.6xx10^(-12))xx6.022xx10^22`  |
|
| 91138. |
An element having atomic mass 107.9 u has FCC lattice. The edge length of its unit cell is 408.6 pm. Calculate density of the unit cell. ["Given, "N_(A)=6.022xx10^(23)"mol"^(-1)]. |
|
Answer» Solution :(a) In simple cubic unit cell, ATOMS are located only at the corners of the cube. The PARTICLES touch one another along the edge. If the edge length of the cube = a, and radius of each PARTICLE is r, the a is related to r as,` a = 2R` The volume of the cubic unit cell `=a^3 = (2r)^3 = 8r^3` Since a simple cubic unit cell contains only 1 atom The volume of the occupied space `= 4/3 pi r^3` Packing Efficiency = `("Volume of space occupied by atom")/("Volume of cubic unit cell") xx 100` `= (4/3 pi r^2)/(8 r^2) xx 100` `= (4PI r^3)/(3 xx 8 r^3) xx 100` `= pi/6 xx 100 = 52.36%` (b) `d = (z.M)/(a^3.N_A)` `= (4 xx 107.9 xx 10^3)/((408.6 xx 10^(-12))^(3) xx 6.022 xx 10^(23))= 10.5 xx 10^(3) kg m^(-3)` 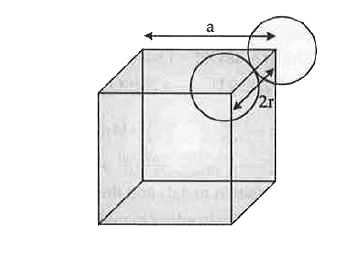
|
|
| 91139. |
i) State Kohlrausch law. ii) What is meant by limiting molar conductance. |
|
Answer» Solution :`E_("cell") = E_(CU^(2+)//Cu^(-))^(0)- E_(Mg^(3+)//mg)^(0) (RT)/(2F) "log"_(10)([Mg^(2+)])/([Cu^(2+)])` `E_("cell") = (0.34 - (2.37)) - (0.059)/(2) "log"_(10)(10^(-3))/(10^(-4))` `E_("cell") = 2.71 - (0.059)/2 "log"_(10)10` `E_("cell") = 2.68 V`. (b) (i) Limiting molar conductivity of an electrolyte can be REPRESENTED as the sum of the individual contributions of the anion and cation of the electrolyte. (ii) When concentration approaches ZERO, the molar CONDUCTANCE is known as limiting molar conductance. |
|
| 91140. |
(a) Calculate Delta_(r)G^(@) for the reaction Mg(s) + Cu^(2+) (aq) to Mg^(2+) (aq) + Cu(s) Given: E_("cell")^(@) = +2.71 V, 1F = 96500 C "mol"^(-1) (b) Name the type of cell which was used in Apollo space programme for providing electrical power. |
|
Answer» Solution :(a) Apply the relation: `Delta_(R)G^(@) =-nFE_("cell")^(@)` Here, n =2, F = 96500 C `mol^(-1)` and `E_("cell")^(@) = 2.71 V` Substituting the VALUES in the equation, we have `Delta_(r)G^(@) =-2 XX 96500 C mol^(-1) xx 2.71 V` `=-523.03 kJ mol^(-1)` (b) `H_(2) - O_(2)` fuel cell was used in Apollo space programme for providing electrical power. |
|
| 91141. |
Calculate e.m.f. of cell for the reaction : Mg_((s))+Cu^(2+)"(0.0001 M)"rarr Mg^(2+)"(0.001 M)"+Cu_((s)) Given that : E_(Mg^(2+)//Mg)^(@)=-2.37V E_(Cu^(2+)//Cu)^(@)=+0.34V |
|
Answer» Solution :CELL equatio :Mg(s) +` Cu^(2+) (aq) to Mg^(2+) (aq)+Cu(s) underset(n=2)` Nernst equaton: `E_(cell)=-0.00591/2log. [Mg^(2+)]/[Cu^(2+)]``E_(cell)=-0.00591/2log. [Mg^(2+)]/[Cu^(2+)]` EMF of the cell, the limiting molar PRODUCTIVITY electroytcan be represent as the sum of limiting molar conductivities of the individual CATION and anion . pplication : kohlraush law is appliedv to calculate the limiting molar conductivityb of any electroyt from the limitinf molar conductivity lambda@ of individual ion.s. when concentrationapproches zero,the molar conductance is KNOWN as limitiomng molar conductance. |
|
| 91142. |
(a) Calculate DeltaG^(@) for the reaction Zn(s) +Cu^(2+) (aq) to Zn^(2+)(aq)+Cu(s) Given : E^(@)" for "Zn^(2+)//Zn= -0.76V and E^(@)" for " Cu^(2+)//Cu=+0.34V R=8.314JK^(-1)"mol"^(-1) F=96500"C mol"^(-1). (b) Give two advantages of fuel cells. |
|
Answer» Solution :(a) `E_("cell")^(@)=E_(Cu^(+)//Cu)^(@)-E_(Zn^(2+)//Zn)^(@)` `=0.34-(-0.76)=1.1V` `DeltaG^(@)=-nFE_("cell")^(@)` Substituting the values, we have `DeltaG^(@)= -2xx96500"C mol"^(-1)xx1.1V` `=-212300"J mol"^(-1)` `=-212.3"kJ mol"^(-1)` (b) Advantages of fuel cell (i) Fuel cells PRODUCE electricity with an efficiency of `70%` compared to thermal PLANTS where the efficiency is `40%`. (ii) Fuel cells are pollution free as the only product formed is water. |
|
| 91143. |
(a) Calculate DeltaG_(f)^(@) of the following reaction Ag^(+)(aq) +CI^(-)(aq) rarr AgCI(s) Given: DeltaG_(f)^(@) (agCI) =- 109 kJ//"mole", DeltaG_(f)^(@)(CI^(-)) =- 129 kJ//"mole", DeltaG_(f)^(@) (Ag^(+)) = 77 kJ//"mole" Represent the above reaction in form of a cell Calculte E^(@) of the cell. Find log_(10).K_(sp) of AgCI (b) 6.539 xx 10^(-2)g of metallic Zn(amu = 65.39) was added to 100ml of saturated solution of AgCI. Calculate log_(10).([Z^(2+)])/([Ag^(+)]^(2)) given that Ag^(+) +e^(-) rarr Ag E^(@) = 0.80V, Zn^(2+) +2e^(-) rarr Zn E^(@) =- 0.76V also find how many moles of Ag will be formed? |
|
Answer» |
|
| 91144. |
(a) Calculate DeltaG^(@)and log K_( c)for the following reaction at 298 K : 2Cr(s) + 3Fe^(2+) (aq) to 2Cr^(3+) (aq) + 3Fe (s) (b) (b) Using the E° values of A and B, predict which is better for coating the surface of iron [E^(@)(Fe^(2+)//Fe) = -0.44 V] to prevent corrosion and why? Given : E_(A^(2+)//A)^(@) = -2.37 V: E_(B^(2+)//B)^(@) = -0.14 V |
|
Answer» Solution :(a) Given that `E_("cell")^(@) = +0.30 V, F = 96500 C mol^(-1)` `2Cr (s) to 2Cr^(3+) + 6E^(-)` `3Fe^(2+)(AQ)+ 6e^(-) to 3Fe (s)` Thus, n=6 Apply the relation: `Delta_(r)G^(@) =-n xx F xx E_("cell")^(@)` or `Delta_(r)G^(@)=-6 xx 96500 C mol^(-1) xx 0.30 V = -173700 J mol^(-1)` or `-173.7 kJ mol^(-1)` `log K_( c) = (nE_("cell")^(@))/0.059` or `log K_( c) = (6 xx 0.30)/0.059` or `log K_( c) = 30.5` (b) A is better for coating the surface of iron. This is because E° value for A is more NEGATIVE than that of Fe. Therefore A has greater TENDENCY for oxidation than Fe. Thus A will oxidise in preference to Fe and protect it from corrosion. |
|
| 91145. |
(a) Calcualte E_("cell")^(@) for the following reaction at 298 K 2Al(s) + 3Cu^(2+) (0.01 M) to 2Al^(3+) (0.01 M) + 3Cu(s) Given: E_("cell") = 1.98 V (b) Using the E^(@) values of A and B predict which is better for coating the surface of iron [E_(Fe^(2+)//Fe)^(@) = -0.44 V] to prevent corrosion and why? Given: E_(A^(2+)//A)^(@) = -2.37 V : E_(B^(2+)//B)^(@) = -0.14 V |
|
Answer» Solution :(a) n=6 in this case `2Al (s) + 3Cu^(2+) (0.01 M) to 2Al^(3+) (0.01 M) + 3Cu(s)` `E_("cell")^(@) = E_("cell") + (0.0591 V)/n log ([AL^(3+)]^(2))/([CU^(2+)])^(3)` `E_("cell")^(@) =E_("cell")^(2)+ (0.0591 V)/6 log ([0.01])^(2)/([0.01])^(2)` `E_("cell")^(@) = 1.98 V + 0.0098 V xx log [0.01]^(-1)` `=1.98 V + 0.0098 V xx 2` `=1.9996 V` = 2V (Rounded) (b) A Is better for coating the surface of iron. Tliis is because `E^(@)`value for A is more negative than that of Fe. THUS A has greater tendency for OXIDATION than Fe. Therefore A will get oxidised in preference to B and PROTECT it from corrosion. |
|
| 91146. |
(A) Calamine is a mineral of calcium (R) Calamine is chemically a sulphate mineral |
|
Answer» Both (A) and (R) are true and (R) is the correct EXPLANATION of (A) |
|
| 91147. |
(A) C_(7)H_(14) an organic compound decolourises Br_(2) solution to produce (B) which combines with strong base NaNH_(2) to produce (C) which does not give white ppt. with AgNO_(3)//NH_(4)OH. (A) again when treated with Hg(OA c)_(2)//H_(2)O+NaBH_(4) toproduce (D) and when treated with HBr/ROOR then OH^(-) to produce (E). Here (D) and (E) are isomeric alcohol, one is optically acetic and other is optically inactive. Q. What is optically active alcohol (E) ? |
|
Answer» `C-C-C-UNDERSET(C)underset(|)(C)-OVERSET(OH)overset(|)(C)-C` |
|
| 91148. |
A caatalyst remains unchanged chemically and physically at the end of the reaction. |
|
Answer» |
|
| 91149. |
(A) C_(7)H_(14) an organic compound decolourises Br_(2) solution to produce (B) which combines with strong base NaNH_(2) to produce (C) which does not give white ppt. with AgNO_(3)//NH_(4)OH. (A) again when treated with Hg(OA c)_(2)//H_(2)O+NaBH_(4) toproduce (D) and when treated with HBr/ROOR then OH^(-) to produce (E). Here (D) and (E) are isomeric alcohol, one is optically acetic and other is optically inactive. Q. What is (C) ? |
|
Answer» `C-C-C-UNDERSET(C-Br)underset(||)(C)-C-C` |
|
| 91150. |
A C_7H_(14)O optically active alcohol is oxidized by jonesreagent to an optically inactive (achiral) ketone. Which of the following compounds meets these facts ? |
|
Answer»
|
|