Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 93401. |
0.6 L of an ideal gas weighs 1.80 g at 27^(@)C and 1 atm pressure. Its approximate molar mass is : |
|
Answer» 36.9 |
|
| 93402. |
0.6 g of a solute is dissolved in 0.1 littre of a solvent which develops an osmotic pressure of 1.23 atm at 27^(@)C. The molecular mass of the substance is |
|
Answer» `149.5 "g mole"^(-1)` |
|
| 93403. |
0.5g of a nonvolatile organic compound (mol.wt. 65) is dissolved in 100mL of "CC"l_(4). If the vapour pressure of pure "CC"l_(4) is 143 mm, what would be the vapour pressure of the solution? (Density of "CC"l_(4) solution is 1.58g//"cc") |
|
Answer» |
|
| 93404. |
0.596g of a gaseous compound containing only boron and hydrogen occupies 484 mL at NTP. When the compound was ignited in excess of oxygen, all its hydrogen was recovered as 1.17g of H_(2)O and all the boron was present as B_(2)O_(3). Find the molecular formula of the compound (B=10.8, H=1) |
|
Answer» Solution :484mL of the gaseous compound at NTP weighs 0.596g. `therefore` molecular weight of the compound =wt. of 1 mole of the compound =wt. of 22400mL at NTP `=(0.596)/(484)XX 22400=27.6` Let the FORMULA be `B_(x)H_(y)` The reaction may be written as, `{:(B_(x)H_(y) + O_(2) ,rarr ,H_(2)O + B_(2)O_(3)),(0.596g,,1.17g):}` APPLYING POAC for H atoms, `yxx` moles of `B_(x) H_(y)=2xx` moles of `H_(2)O` `y xx (0.596)/(27.6) = (2xx 1.17)/(18)` y=6 Further, for the formula `B_(x)H_(y)`, mol wt. =27.6 `therefore 10.8x + 1y= 27.6` `10.8x + 6= 27.6` x=2 Hence the molecular formula is `B_(2)H_(6)` |
|
| 93405. |
0.58 g of hydrocarbon on combustion gave 0.9 g water. The percentage of carbon is about : |
|
Answer» 75.8 |
|
| 93406. |
0.53 gm of Na_(2)CO_(3) has been dissolved in 100 ml of a sodium carbonate solution. The normality of the solution will be |
|
Answer» `(N)/(5)` So NORMALITY of the solution will be `(N)/(10)`. |
|
| 93407. |
0.5 normal solution of a salt placed between two platnum electrodes 2.0 cm. apart and of area of cross section 4.0 sq. cm. has a resistance of 25 ohms. Calculate the equivalent conductivity of solution. |
|
Answer» Solution :1st step-Calculation of specific conductivity. here, L=2.0 cm, a=4.0`cm^(2),""R=25`ohms `therefore`CONDUCTANCE`G=(1)/(R)=(1)/(25)ohm^(-1),"Cell constant"=(1)/(a)=(2cm)/(4CM^(2))=(1)/(2)cm^(-1)` `therefore`Sp. Conductivity (`kappa`)=Observed conductance`xx`cell constant`=(1)/(25)Omega^(-1)xx(1)/(2)cm^(-1)=0.02Omega^(-1)cm^(-1)` 2nd step-Calculation of EQUIVALENT conductivity`wedge_(eq)=kappaxx(1000)/(c_(eq))` Here, `c=0.5N,kappa=0.02ohm^(-1)` (calculated above) `thereforewedge_(eq)=((0.02Omega^(-1)cm^(-1))xx(1000cm^(3)L^(-1)))/((0.5" g eq "L^(-1)))=40Omega^(-1)cm^(2)eq^(-1)` or `40" S "cm^(2)eq^(-1)` |
|
| 93408. |
0.5 mole of SO_2 gas at 27^@C is expanded in reversible adiabatic condition to make volume 8 times.Final temperature (in K) and work done by gas (in Cal) respectively are x and y.Report your answer as y/x. (Take ideal behaviour of gas, R=2 Cal/K mol and 2^(1.2)=2.3) |
|
Answer» `W=nC_v(T_2-T_1)=0.5xx3 R(150-300)=0.5xx3xx2(-150)=-450`CAL |
|
| 93409. |
0.5 mole of electron is passed though two electrolytic cells in series. One contains silber ions, and the other zinc ions. Assume that only cathode reaction in each cell is the reduction of the ion to the metal. How many gm of each metals will be deposited. |
|
Answer» |
|
| 93410. |
0.5 mole of eachH_(2),SO_(2) and CH_(4) are kept in a container. A holewas made in the container. After 3 hours, the order of partial pressures in the container will be |
|
Answer» `P_(SO_(2))gtp_(CH_(4))gtP_(H_(2))` `:.p_(SO_(2))gtp_(CH_(4))gtp_(H_(2))` |
|
| 93411. |
0.5moleof anidealmonoatomic gas atSTP conditionsundergoes a process, if the finalvolumeof gas is(22.5xxe) lit,then theentropy change in thid processin k/J/mol is .(Given: Processisobaric ) (Fill your answerby multiplyingit with (100)/(R)) |
|
Answer» Solution :`(V_(1))/(V_(2))= (T_(1))/(T_(2)) rArr (22.7//2)/(22.7. e)= (273)/(T_(2))rArr"" T_(2) = 273.(2E)` `DeltaS = nC_(p)LM.(T_(2))/(T_(1))""0.5 xx (5)/(2)R xx LN. ((273).(2e))/((273))` `= (5)/(4) R(ln 2e) =(5)/(4) R(ln 2 + ln e)""thereforeif LN2 =0.7` `= (5)/(4) Rxx(1.7) xx(100)/(R)""= 212.5` |
|
| 93412. |
0.5 mole each of two ideal gases A(C_(v)=3/2R)andB=(C_(v)=5/2R) are taken in a container and expanded reversibly and adiabatically from V = 1 L to V = 4 L starting from initial temperature T = 300 K. Find DeltaH for the process in (cal/mol). |
| Answer» SOLUTION :`-900" CALORIES"` | |
| 93413. |
0.5 mole each of H_(2), SO_(2) & CH_(4) are kept in container. A hole was made in the container. After 3 hours the order of partial pressures in the container will be: |
|
Answer» `P_(SO_(2)) GT P_(CH_(4)) gt P_(H_(2))` |
|
| 93414. |
0.5 molar NaCl and 0.8 molal urea solutions are formed to be isotonic at 27^(@)C then the degree of dissociation of NaCl under these consitions is reported as xxx10% . What is the value of 'x' ? |
|
Answer» |
|
| 93415. |
0.5 molal aqueous solution of a weak acid (HX) is 20% ionised. If K_(f) of water is 1.86 K kg "mol"^(-1) , the lowering in freezing point of the solution is : |
|
Answer» 0.56 K If `ALPHA` is the DEGREE of DISSOCIATION, then moles after dissociation. `{:(1-alpha,,,alpha,,alpha):}` TOTAL moles after dissociation `=1-alpha+alpha+alpha=1+alpha` `i=(1+alpha)/(1)=(1+0.2)/(1)=1.20` `DeltaT_(f)=iK_(f)` `=1.20xx1.86xx0.5=1.12K` |
|
| 93416. |
0.5 mol of H_(2)SO_(4) is mixed with 0.2 mol of Ca(OH)_(2) . The maximum number of moles of CaSO_(4) formed is |
|
Answer» 5 |
|
| 93417. |
0.5 mol of BaCl_2is mixed with 0.2 mol ofNa_3PO_4 . The maximum number of mol of Ba_3(PO_4)_2that can be formed is : |
|
Answer» 0.7 `3BaCl_2 + 2Na_3 PO_4 to Ba_3 (PO_4)_2 + 6NaCl` 2 mol of `Na_3PO_4` given= 1 mole of `Ba_3(PO_4)_2` 0.2 mol of `Na_3PO_4` will GIVE = 0.1 mol of `Ba_3(PO_4)_2` |
|
| 93418. |
0.5 molal aqueous solution of a weak acid (HX) is 20% ionised. If K_(f) for water is 1.86 K kg mol^(-1), the lowering in freezing point of solution will be : |
|
Answer» 0.56 For DESSOCIATION of electrolyte, `alpha=((i-1))/((n-1))or0.2=((i-1))/((2-1))` i=1+0.2=1.2 `DeltaT_(F)=I K_(f)m` `=(1.2)xx(1.86 K m^(-1))xx(0.5m)=1.12 K` |
|
| 93419. |
0.5 mol each of H_(2), SO_(2) and CH_(4) are ketp in a container. A hole was made in the container. After 3 hours, the order of partial pressure in the container will be : |
|
Answer» `pSO_(2) gt pCH_(4) gt pH_(2)` `H_(2) gt CH_(4) gt SO_(2)` `:.` the order of partial pressures in the container will be `: p SO_(2) gt pCH_(4) gt pH_(2)` |
|
| 93420. |
0.5 M glucose solution is iso-osmotic with which of the following solutions ? |
|
Answer» 0.10 M NACL |
|
| 93421. |
0.5 M ammonium benzoate is hydrolyzed to 0.25 percent, hence its hydrolysis constant is |
|
Answer» `2.5 xx 10^(-5)` According to Ostwald dilution law. `K = (ALPHA^(2)C)/(1-alpha) "" ( :. alpha = (.25)/(100))` `K = alpha^(2)C "" ( because 1- alpha = "Very SMALL")` `K = (0.25)/(100) xx (0.25)/(100)xx 0.5 , K = 3.125 xx 10^(-6)` |
|
| 93422. |
0.5 L of a saturated solution of Ag_(2)CrO_(4) is mixed with 0.5 L of 2 xx 10^(-6) M AgNO_(3). If concentration of [CrO_(4)^(2-)]after mixing is (10^(-6)/2)M and none of the ions undergo hydrolysis, then calculate a four digit number abcd where, ab = (K_(sp) of Ag_(2)CrO_(4))/(10^(-19) and cd = conductivity of final solution in terms of 10^(-8)Omega^(-1) cm^(-1). Assume temperature of the solution to be 298 K [Given data: Molar conductance at infinite dilution in Omega^(-1) cm^(2) mol^(-1) are lambda_(m)^(infty)(OH^(-)) = 200, lambda_(m)^(infty)NO_(3)^(-) = 75, lambda_(m)^(infty)Ag^(+) = 50 lambda_(m)^(infty)CrO_(4)^(2-) = 100 |
|
Answer» |
|
| 93423. |
0.5 L of 1.0 M NaCl solution is electrolysed for 965 a using a current of 5 ampere. What will be the pH of the solution after the electrolysis? |
|
Answer» Solution :`NaCl+H_(2)O OVERSET("ELECTROLYSIS")to(1)/(2)H_(2)+(1)/(2)Cl_(2)+NaOH` amount of NaCl present in 0.5 L of 1.0 M NaCl=0.5 mole QUANTITY of electricity passed=`965xx5C=4825C` 1 mole of NaCl is decomposed by 96500C `therefore4825`C will decompose `NaCl=(4825)/(96500)"mole"=0.05`mole NaOH formed in the solution will also be 0.05 mole volume of the solution`=0.5L` `therefore`Molarity of NaOH in the solution`=(0.05)/(0.5)=0.1M=10^(-1)M` `thereforepOH=1` or `pH=14-1=13`. |
|
| 93424. |
0.5 gm of an oxalate was dissolved in water and the solution raised to 100 ml. 10 ml of this solution when titrated with N/20 KMnO_4 required 10 ml of KMnO_4. Calculate the % of oxalate ion in the sample. (K = 39, Mn = 55) |
|
Answer» |
|
| 93425. |
0.5 g of NaOH is required by 0.4 gm of a polybasic acid H_(n)A (Molecular weight = 96 gm) for complete neutralisation .Value of 'n' would be : (Assume all H atom are replaced )- |
|
Answer» |
|
| 93426. |
0.5 gm of an organic substance containing phosphorous was heated with conc. HNO_(3) in the Carius tube. The phosphoric acid thus formed was precipitated with magnesia mixture (MgNH_(4)PO_(4)) which on ignition gave a residue of 1.0 gm of magnesium pyrophosphate (Mg_(2)P_(2)O_(7)). The percentage of phosphorous in the organic compound is : |
|
Answer» 0.5585 |
|
| 93427. |
0.5 g of metal nitrate gave 0.43 g of metal sulphate |
|
Answer» The equivalent wt. of the metal is `0.38` Metal sulphate ` = M_(2)(SO_(4))_(x)` Eq. of `Mn(NO_(3))_(x) = " Eq. of " M_(2)(SO_(4))_(x)` Let Eqv. Wt. of metal = `E_(M)` `(0.5)/(E_(M) + 62) = (0.43)/(E_(M) + 96/2) ` ` rArr0.5E_(M) + 0.5 xx 48 = 0.43 xx E_(M) + 62 xx 0.43` ` rArr0.5E_(M) + 24 = 0.43E_(M) + 26.66` ` RARR(0.5 - 0.43) E_(M) = 26.66 - 24` ` rArr0.07E_(M) = 2.66` ` :. E_(M) = (2.66)/(0.07) = 38` As valence of metal is x Atomic wt. = `38 x` |
|
| 93428. |
0.5 g of KCl was dissolved in 100 g of water and the solution originally at 20^@C froze at - 0.24^@C. Calculate the percentage dissociation of salt.Given : K_ffor water = 1.86 K kg/mol, At, mass : K= 39 u, Cl = 35.5 u. |
|
Answer» Solution :`Delta T_f = 0^@- (- 0.24^@C) = 0.24^@C "or" 0.24K` Apply the following equation ` M_2 = (K_f XX w_1 xx 1000)/((Delta T_f) xx w_1)` Substituting the values in this equation, we have `M_2 = (1.86 K kg "mol"^(-1) xx 0.5 g xx 1000 g kg^(-1))/(0.24 K xx 100 g) = 38.75 g "mol"^(-1)` van.t Hoff factor, i = Normal mol. mass / Abnormal mol. mass `= (74.5 g "mol"^(-1))/(38.75 g "mol"^(-1)) = 1.92` ` alpha = (i-1)/(n-1)` ,where n is the number of particles after dissociation In the case of KCL, n = 2 Substituting the values in the equation above `alpha = (1.92 - 1)/(2-1) " or " alpha = (0.92)/(1) = 0.91` Percentage dissociation = 0.92 x 100 = 92% |
|
| 93429. |
0.5 g of fuming H_(2)SO_(4) (oleum ) is diluted with water . The solution is completely neutralised by 26.7 mL of 0.4 N naOH .Find the percentage of free SO_(3) in the sample of oleum. |
|
Answer» Solution :REACTIONS involved are `SO_(3) + 2NaOH to Na_(2)SO_(4) +H_(2)O ` `H_(2)SO_(4) +2NaOH to Na_(2)SO_(4) +2H_(2)O ` Eq. wt of `SO_(3) = 80/2 = 40 ` Eq. wt of `H_(2)SO_(4) = 98/2 = 49 ` Now m.e of `SO_(3)`+ m.e of `H_(2)SO_(4)` = m.e of NaOH ` :. " eq of " SO_(3) xx 1000 eq . of H_(2)SO_(4) xx 1000 = 0.4 xx 26.7 ` Suppose the wt. of `SO_(3) ` is x G . ` :. ` wt of `H_(2)SO_(4) = (0.5 - x) g ` ` :. x/40 +((0.5 - x))/49 = 0.4 xx 26.7 x = 0.1036 g ` `:. "" % of SO_(3) = (0.1036)/(0.5) xx 100 = 20.67 % ` |
|
| 93430. |
0.5 g of fuming H_(2)SO_(4) (oleum) is diluted with water. The solution requires 26.7 ml of 0.4 N NaOH for complete neutralization. Find the % of free SO_(3) in the sample of oleum. |
|
Answer» |
|
| 93431. |
0.5 g of an organic compound containing nitrogen on Kjeldahlising required 29 mL of N/5H_2SO_4 for complete neutralisation of ammonia. The percentage of nitrogen in the compound is : |
|
Answer» 34.3 |
|
| 93432. |
0.5 g KCl was dissolved in 100 g water and the solution originally at 20^(@)C, froze at -0.24^(@)C. Calculate the percentage ionization of salt. K_(f) per 1000 g of water =1.86^(@)C. |
|
Answer» Solution :Observed mol.Mass is obtained from the given data, i.e., `w_(2)="0.5 g,"w_(1)="100 g,"M_(1)="18 g mol"^(-1)" for "H_(2)O, DeltaT_(f)=0-(-0.24)=0.24^(@)C` `M_(2)=(1000K_(f)w_(2))/(DeltaT_(f)xxw_(1))=("1000 g kg"^(-1)xx"1.86 K kg mol"^(-1)xx"0.5 g")/("0.24 K"xx"100 g")="38.75 g mol"^(-1)` Calculated (theoretical) mol mass of KCl `=39+35.5="74.5 g mol"^(-1)` `therefore"i"=("Calculated mol mass")/("Observed mol mass")=(74.5)/(38.75)=1.92` Now, KCl dissociated as `{:(,KCl,hArr,K^(+),+,CL^(-)),("Initial moles","1 mole",,0,,0),("Moles after disso.",1-alpha,,alpha,,alpha):}` `"Total no. of moles after dissociation "=1-alpha+alpha+alpha+=1+alpha""therefore""i=(1+alpha)/(1) or alpha=i-1=1.92 -1=0.92` PERCENTAGE ionization `=0.92xx100=92%`. |
|
| 93433. |
0.5 F of electric current was passed through 5 molar solution of AgNO_(3), CuSO_(4) " and " AlCl_(3) connected in series. Find out the concentration of each of the electrolyte after the electrolysis. |
|
Answer» SOLUTION :Given : Quantity of electricity, Q = 0.5 F <BR> Concentration of solution, C = 5 M Solution : (i) For `AgNO_(3)` 1 mol of `Ag^(+)=1F` `""0.5F= 0.5` mol of `AgNO_(3)` Concentration of `AgNO_(3)` after electrolysis `""=5-0.5` `""=4.5 M` (ii) For `CuSO_(4)` 1 mol of `CuSO_(4) " (or) " Cu^(2+)=2F` 2F = 1 M `CuSO_(4)` `0.5F=1/2 times 0.5=0.25M` Concentration of `CuSO_(4)` after electrolysis `""=5-0.25` `""=4.75M` (iii) For `AlCl_(3)` 1 mol of `AlCl_(3)" Br "Al^(3+)=3F` `3F=1M" "AlCl_(3)` `0.5=1/3 times 0.5` `""=0.5/3=0.167M` Concentration of `AlCl_(3)` after electrolysis `""=5-0.167` Concentration of `AlCl_(3)` after electrolysis `""=4.833M` |
|
| 93434. |
0.5 F of electric current was passed though 5 molar solutions of AgNO_(3), CuSO_(4) and AlCl_(3) connected in series. Find out the concentration of each of the electrolyte after the electrolysis ? |
| Answer» Solution :`AgNO_(3), 4.5M, CuSO_(4), 4.75M, AlCl_(3),4.839M` | |
| 93435. |
A sample of 0.50 g of an organic compound was treated according to Kjeldahl’s method. The ammonia evolved was absorbed in 50 ml of 0.5 M H_(2)SO_(4). The residual acid required 60 mL of 0.5 M solution of NaOH for neutralisation. Find the percentage composition of nitrogen in the compound. |
|
Answer» `%N= (1.4 XX "meq of ACID to neutralise" NH_(3))/("weight or organic compound(G)")` |
|
| 93436. |
0.4g of an organic compound gave 0.188g of silver bromide by a halogen estimation method. The percentage of bromine in the compound is : (at.mass of Ag=108, Br=80) : |
|
Answer» `39.8%` `=(80)/(188)xx0.188=0.80g` `%Br=(0.08)/(0.4)xx100=20%` |
|
| 93437. |
0.48 g of a volatile substance upon vapourisation gives 112 ml vapours at STP. Ratio of rate of diffusion of vapours of volatile substance to H_2(g) is (assume vapours behave ideally) |
|
Answer» `1`/`sqrt(12)` |
|
| 93438. |
0.465g of an organic compound upon combustion produced 1.32g of CO_(2) and 0.315g of H_(2)O. 0.2325g of the same compound gave 27.8 mL of dry N_(2) at NTP. If the compound contained C, H and N find its formula |
|
Answer» Solution :Moles of C in `CO_(2)=1 xx` moles of `CO_(2) = (1.32)/(44)= 0.03` moles of H in `H_(2)O=2xx` moles of `H_(2)O=2 xx (0.315)/(18)= 0.035` Moles of N in `N_(2)=2xx` moles of `N_(2)=2 xx (27.8)/(22400)= 0.0025` Now, 0.0025 mole of N is contained in 0.2325g of the compound. `therefore` moles of N in 0.465g of the compound `=0.0025 xx (0.465)/(0.2325)=0.005` `therefore` moles of `C: H: N= 0.030: 0.035 : 0.005` `=30: 35: 5` `=6: 7: 1` `therefore` empirical FORMULA is `C_(6)H_(7)N` |
|
| 93439. |
0.46 g ofan organic compound containing C,H oxygen was heatedstronglyin steam of N_(2) gas . The gaseous mixture thus obtained was passed over heated coke at 1373 K and then passed through warm solution of iodine pentoxide when 2.54 g of iodine. The percentage of O_(2) in the compound is |
|
Answer» `69.59` `= 32/254 xx (2.54)/(0.46) xx 100 = (32)/(0.46) = 69.56%` (b) , (c ) and (d) are not POSSIBLE. |
|
| 93440. |
0.45g of a dibasic organic acid upon combustion produced 0.44g of CO_(2) and 0.09g of H_(2)O. 0.76g of its silver salt when ignited gave 0.54g of pure silver. What is the fomula of the acid? (Ag=108) |
|
Answer» Solution :Moles of C in `CO_(2)=1 xx` moles of `CO_(2)` `=1 xx (0.44)/(44)= 0.01` Weight of `C= 0.01 xx 12= 0.12g` Moles of H in `H_(2)O=2 xx` moles of `H_(2)O` `2 xx (0.09)/(18)=0.01` Weight of `H= 0.01 XX1= 0.01g` Weight of O = wt. of acid - (wt. of C + wt. of H) `=0.45-(0.12+ 0.01)g` = 0.32g Mole of `O= (0.32)/(16)= 0.02` Mole of `C: H: O= 0.01 : 0.01: 0.02` `=1: 1: 2` Empirical formula is `CHO_(2)` Now 0.76g of Ag salt of the dibasic acid gives 0.54 g of pure silver, i.e., `{:("dibasic acid",rarr Ag " salt"rarr,Ag),(,0.76g,0.54g),(,"(contains2 Ag atoms)",):}` We know that the Ag salt of the dibasic acid is formed by the replacement of 2H atoms of the acid by 2Ag atoms. Applying POAC for the Ag atoms, moles of Ag atom in Ag salt= moles of Ag in the product `2XX` moles of Ag salt= moles of Ag in the product `2 xx (0.76)/("mol. wt. of Ag salt") = (0.54)/(108)` Molecular weight of the salt = 304 `therefore` molecular weight of the acid = mol. wt of salt `-2 xx` at wt of Ag + 2`xx` at. wt. of H `=304 -216+2=90` Hence, `("molecular formula weight")/(" empirical formula weight")= (90)/(45)=2` `therefore` molecular formula is `(CHO_(2))_(2)` i..e., `(COOH)_(2)` |
|
| 93441. |
0.450 gm of an aromatic organic compound (A) on ignitin gives0.905 gm CO_(2) and 0.15gm H_(2)O 0.350gm of (A) on hydrolysis with Ca(OH)_(2) yields(B) which on mild reduction gives an opticallyactive compound(C). On heating(C) with I_(2) and NaOH, iodofrom is producedalong with (D). WithHCl, (D) gives a solid, which is more soluble in hotwater thanin cold. Idenify (A) to (D) with proper explanaion. |
|
Answer» Solution :Percentage of `C = (12)/(44) xx ("Wt. of" CO_(2)xx100)/("Wt. of compound")` `= (12xx0.905xx100)/(44xx0.450) = 54.84%` Percentage of `H = (2)/(18) xx ("Wt. of" HO_(2)xx100)/("Wt. of compound")` `= (2xx0.15xx100)/(18xx0.450) = 3.7%` Percentage of `Cl = (35.5)/(143.5) xx ("Wt. of" AGCL xx 100)/("Wt. of compound")` `= (35.5xx0.574xx100)/(143.0.350) = 40.57%` Molecular mass of `(A) = 2 xx V.D. = 2xx87.5 = 175.0` 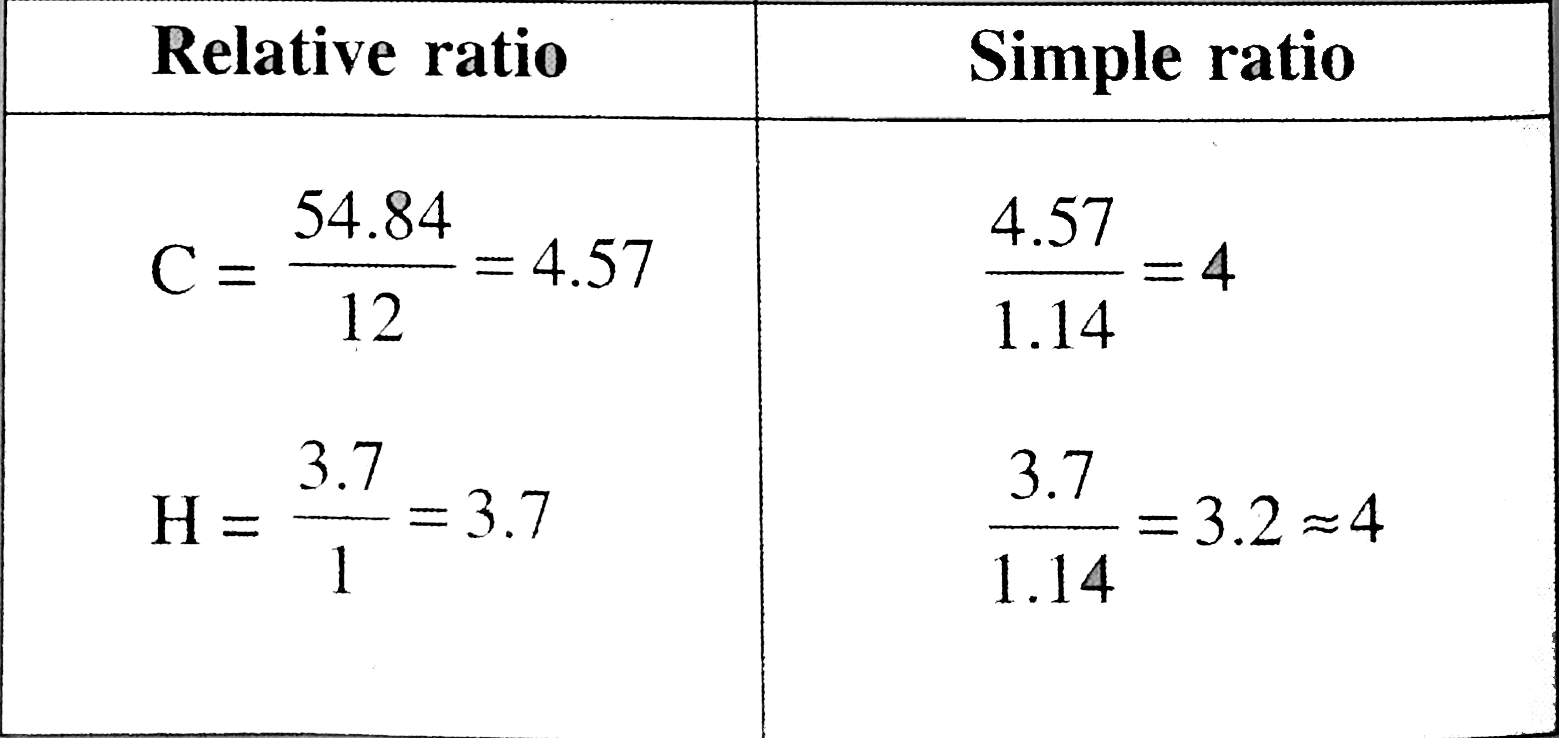  Empirical formula`= C_(4) H_(4) Cl` `N = (MFW)/(EFw) = (175.0)/(87.5) = 2` Molecular formula `= C_(8) H_(8)Cl_(2)` `D.U` in `(A) = ((2n_(C) + 2) - (n_(Cl) + n_(H)))/(2)` `= ((2xx8+2)-(2+8))/(2) = 4^(@)` `4 D.U` in `(A)` suggests benzene ring with two `Cl` and two `C` atoms. REACTIONS with`Ca(OH)_(2)` of `(A)` suggests that two `Cl`atomare in the side chain becuasethere is no `EWG` present in the ring. Two `Cl` atoms can be vicinal or gemial lodoform reaction suggests that there must be`(overset(O)overset(||)(-C-) CH_(3))` or `(CH_(3) - underset(|)(C) - OH)` group. So ketone can be OBTAINED from `(A)` when two `Cl`atoms are in gemial postion. Reaction: 
|
|
| 93442. |
0.45 g of an organic compound (A) on ignition gives 0.905 g CO_2 and 0.185 gH_2O.0.35 g (A) on boiling with HNO_3and adding AgNO_3solution gives 0.574 g of AgCl. The vapour density of (A) is 87.5. (A) on hydrolysis with Ca (OH)_2yields (B) which on mild reduction gives an optically active compound (C). On heating (C) with I_2 and NaOH, iodoform is produced along with (D). With HCI, (D) gives a solid which is markedly more soluble in hot water than in cold. Identify (A), (B), (C) and (D). |
Answer» SOLUTION :
|
|
| 93443. |
0.45 g of an acid of molecular weight 90 was neutralised by 20 mL of 0.5 N caustic potash .The basicity of the acid is |
|
Answer» 1 |
|
| 93444. |
0.45 g of an acid ( mol. Mass = 90 ) is neutralised by 20 mol of 0.5 N NaOH solution. The basicity of the acid is : |
|
Answer» 1 1000 ml of 1 N NaOH solution neutralise acid `=(0.45 xx 1000 xx 1)/(20 xx 0.5)` = 45 g EQ. WT of acid = 45 g BASICITY `=("Mol. wt")/("Eq. wt ")=(90)/(45)=2` |
|
| 93445. |
0.45 g an acid (mol wt.=90) required 20 ml of 0.5 N KOH for complete neutralization. Basicity of acid is |
|
Answer» 1 `therefore"Eq. WT"=(0.45xx1000)/(0.5xx20)=45` `therefore"BASICITY"=("Molec. Wt")/("Eq. wt")=(90)/(45)=2` |
|
| 93446. |
0.44 g of a monohydric alcohol when added to methylmagnesium iodide in ether liberates at S.T.P.,112 cm^(3) of methane. With PCC the same alcohol forms a carbonyl compound that answers silver mirror test. The monohydric alcohol is |
|
Answer» `H_3C - UNDERSET(OH)underset(|)CH-CH_2 - CH_3` |
|
| 93447. |
0.440 g of a substance dissolved in 22.2 g of benzene lowered the freezing point of benzene by 0.567^(@)C. The molecular mass of the substance (K_(f)=5.12^(@)kg C mol^(-1)) |
|
Answer» `178.9` |
|
| 93448. |
0.44 g of a monohydric alcohol when added to methyl magnesium iodide in ether liberates at STP 112 cm^3 of methane with PCC the same alcohol form a carbonyl compound that answers silver mirror test. Identify the compound. |
|
Answer» Solution :0.44g of a monohydric alcohol liberates `112 cm^3` of methane. `underset(1 "MOLE")(R- OH + CH_3MgI to underset(1" mole")(CH_4) + mgI(OR)` `:.` ass of monohydric alcohol which gives `22400 cm^3` of methane `=(22400 xx 0.44)/112= 88` `C_5H_12O` molecular formula has MASS number 88 and it shows eight possible isomers. But neopentyl alcohol reacts with PCC to form neopentyl aldehyde, which shows positive SILVER mirror test. Therefore, compound is, neopentyl alcohol (or) 2, 2-dimethyl propan-1-ol. `CH_3- underset(CH_3) underset(|)OVERSET(CH_3) overset(|)C - CH_2OH` |
|
| 93449. |
0.44 g of a monohydric alcohol when added to methyl magnesium iodide in ether lilberates at STP 112 cm^(3) of methane with PCC the same alcohol form a carbonyl compound that answers silver mirror test. Identify the compound. |
Answer» Solution :`R-OH + CH_(3) MgI to CH_(4)` +  `22400 cm^(3)` at STP is `112 cm^(3)` Mass of alcohol `=(0.44 XX 22400)/112 = 88 G` Alcohol reacts with PCC to give a carboxyl compound which answers silver mirror test. Therefore, the alcohol MUST be a PRIMARY alcohol which on oxidation GIVES aldehyde with mass of 88 g. So the probable primary alcohol is `(CH_(3))_(2)CH-CH_(2)-OH`. |
|
| 93450. |
0.44 g of a hydrocarbon on complete combustion with oxygen gave 1.8g water and 0.88 g carbon dioxide. Show that these resutls are in asccordance with the law of conservation of mass. |
|
Answer» Solution :A hydrocarbon is a compound which consists of carbon and hydrogen only. It UNDERGOES combustion FORMING carbon dioxide and water as products. Formula of Carbon dioxide=`CO_(2)`, Molecular MASS `=12+32=44g`. Formula of water `=H_(2)O`. Molecular mass =2+16=18g Mass of carbon in 0.88 g of `CO_(2)=(12)/(44)xx0.88=0.24g` Mass of hydrogen in 1.8 g of `H_(2)O=(12)/(44)xx1.8=0.20g` Mass of hydrogen in 1.8g of `H_(2)O=(2)/(18)=0.20g` TOTAL masses of carbon and hydrogen in the products `=0.24+0.20=0.44g` This is equal to the mass of hydrocarbon before combustion. Thus, the results are in accordance with the LAW of conservation of mass. |
|