InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 651. |
Differentiate the following functions with respect to x: x+ sin x = sin y |
|
Answer» |
|
| 652. |
If f(x)=int_(-1)^(x)abs(t)dt, x ge 1, then |
|
Answer» F is CONTINUOUS at x=0 but `f^(')` is not continuous |
|
| 653. |
int _(0) ^(pi//2) sin phi cos phi sqrt((a^(2) sin ^(2) phi cos ^(2)))d phi a ne b a gt 0, b gt 0) |
|
Answer» |
|
| 654. |
If f_(1)(x) = 2x + 3, f_(2)(x) = 3x^(2) + 5, f_(3)(x) = x + cos x are defined from R rarr R, then f_(1), f_(2) and f_(3) are |
|
Answer» ONE-one onto |
|
| 655. |
sinh^(-1)2+sinh^(-1)3 = x rArr "coshx"is equal to |
|
Answer» `1/2(3 SQRT(5)+2sqrt(10))` |
|
| 656. |
If I=int_(3)^(4) (1)/(3sqrt(logx))dxthen |
|
Answer» `0.92 LT I lt 1` |
|
| 658. |
Find the equation of ellipse whose vertices are (5,0) and (-5,0) and whose focus lies on the line 3x-5y=9 |
|
Answer» |
|
| 659. |
The solution set of the inequation 5^((1//4)(log5 x)^(2)) ge 5x^((1//5)(log5 x)) is |
|
Answer» `(0,5^(-2sqrt(5))]` |
|
| 661. |
If the solution of the differential equation (dy)/(dx)-y((x^(4)+3x^(2))/((x^(2)+1)^(2)))=(4x+3)e^((x^(3))/(e^(2)+1)) is in the form y =f(x) (where f(0)=1), then f(A)+f(-1) is |
|
Answer» `2sqrt(E)` `impliesye^((-x^(5))/(x^(2)+1))=int(4x+3)dx` `impliesf(x)=y=(2x^(2)+3x+1)e^((x^(3))/(x^(2)+1)` `impliesf(1)=6sqrt(e)` & `f(-1)=0` `impliesf(-1)=0` |
|
| 662. |
If X is a Poisson variate such that P(X=2)=9P(X=4)+90P(X=6), then the ordered pair (Mean (X), Variance (X) = |
| Answer» ANSWER :B | |
| 663. |
Equation of a hyperbola such that the distance between the foci is 16 and eccentricity is sqrt(2) is |
|
Answer» `x^2 - y^2 = 16` |
|
| 664. |
If a,b,c are in A.P.and f(x)=|(x+a,x^2+1,1),(x+b, 2x^2-1,1),(x+c,3x^2-2 , 1)|, thenf'(x)is : |
|
Answer» 0 |
|
| 665. |
If n is positive integer then greatest value of x(a-x)^non (0,a) is |
|
Answer» 0 |
|
| 666. |
The values of (sqrt3+i)^(1//4) are |
|
Answer» `2^(1//4)CIS[(2kpi+pi//6)/(4)],k=0,1,2,3` |
|
| 667. |
S is a sample spaceS= (x in N : 1 x le 100) and E=(x : x(+1)(x-1) in S) . Then P(E)= |
|
Answer» `1//10` |
|
| 668. |
Let f be the real valued differentiable function on R such that e^(-x)f(x)=3/(e^(2))+4e^(-x) int_(2)^(x) sqrt(2t^(2)+6t+5)dt AA x in R and let g(x)=f^(-1) (x) then [g^(')(3)]+[|g^('')(3)|] is equal to _____ (where [.] denote the greatest integer function) |
|
Answer» So, `g^(')(f(x)).f^(')(x)=1` `g^('')=(f(x))=-(f^('')(x))/((f^(')(x))^(3))` So, `g^(')(3)=1/23` and `g^('')(3)=(-43)/(5(23)^(3))` |
|
| 669. |
If O is the circumcentre and O' the orthocenter of DeltaABC prove that (i) SA+SB+SC=3SG, where S is any point in the plane of DeltaABC. (ii) OA+OB+OC=OO' Where, AP is diameter of the circumcircle. |
Answer» Solution :Let G be the centroid of `DeltaABC`, first we shall show that CIRCUMCENTRE O, ORTHOCENTER O' and centroid G are collinear and O'G=2OG. 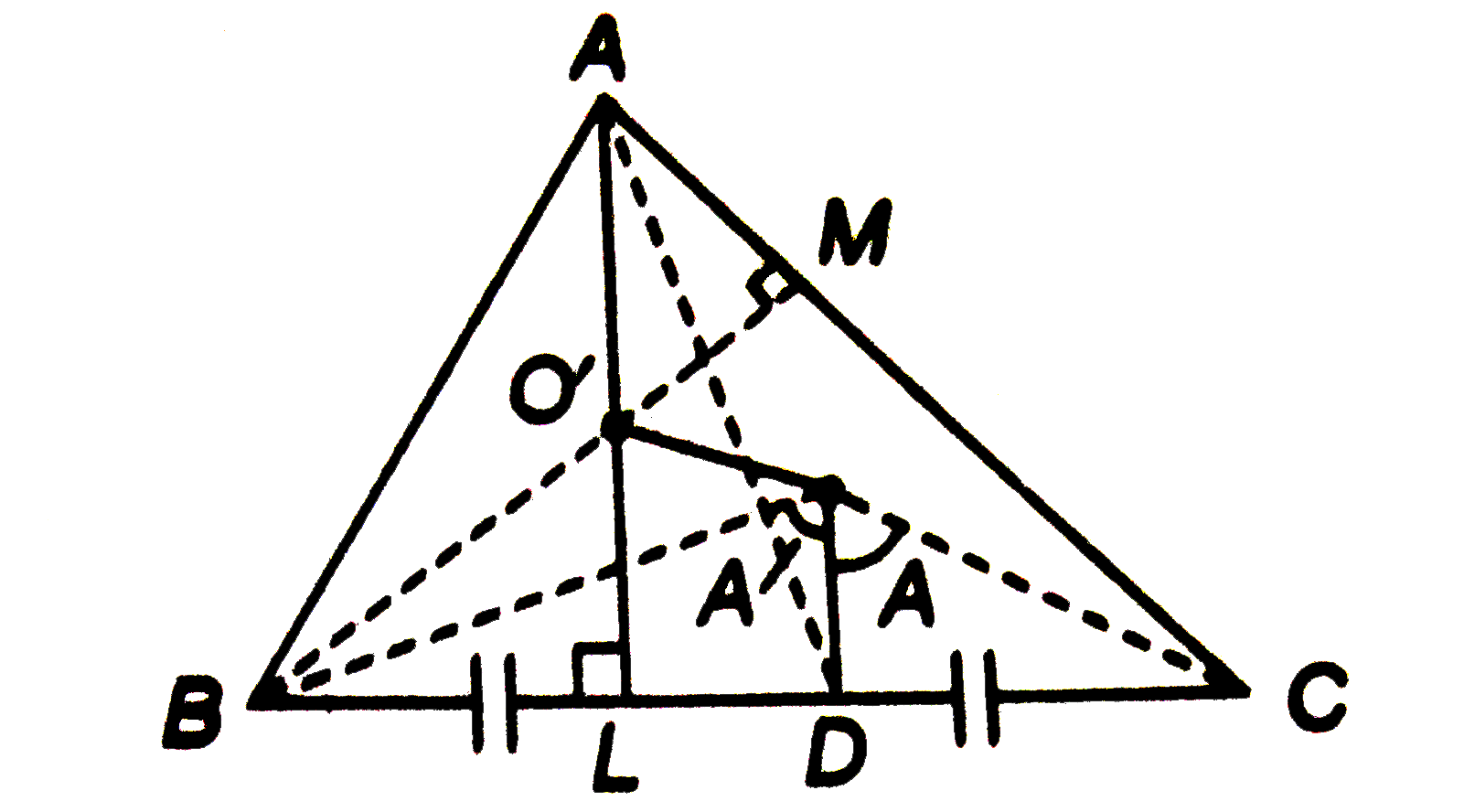 Let AL and BM be perpendiculars on the sides BC and CA, respectively. Let AD be the median and OD be the perpendicular from O on side BC. iff R is the circumradius of circumcircle of `DeltaABC`, then OB=OC=R. In `DeltaOBD,` we have OD=R cosA. . . (i) In `DeltaABM,AM=AB cos A=c cosA`. . . (ii) FORM `DeltaAO'M,AO'=AMsec(90^(@)-C)` =c cos A cosec C `=(c)/(SINC)*cosA=2RcosA ""(because(a)/(sinA)=(b)/(sinB)=(c)/(sinC)=2R)` `AO'=2(OD)`. . . (iii) Now, `DeltaAGO' and DeltaOGD` are similar. `therefore(OG)/(O*G)=(GD)/(GA)=(OD)/(AO')=(1)/(2)`[using Eq. (iii)] `implies 2OG=O'G` (i) We have, `SA+SB+SC=SA+(SB+SC)` `=SA+2SD`(`because` D is the mid-point of BC) `=(1+2)+SG=8SG`. (ii) On REPLACING S by O in Eq. (i), we get `OA+OB+OC=3OG` `=2OG+OG=GO'+OG` `=OG+GO'+O O'`. |
|
| 670. |
ABCDE is a pentagon. If the sum of the vectors bar(AB),bar(AE), bar(BC), bar(DC), bar(ED), bar(AC) is lambda bar(AC) then find the value of lambda. |
|
Answer» |
|
| 672. |
Let{:{(|x-1|+a, x lt 1), (2x+3, x ge 1):} if f(x)has a local minima at x=1 , then |
| Answer» Answer :A | |
| 673. |
p: Two circles are congruent if and only if their radii are equal. Check the validity of statement P |
|
Answer» Solution : In ORDER to prove the statement "p if and only if q", we need to show that (i) If p is TRUE, then q is true and (ii) If q is true, then p is true or show that `~q rArr ~p`. Now, Let p : Two circles are congruent. q : Radius of two circles are equal. Assume that pis true i.e., circles are congruent, we KNOW that two figures are congruent thentheir areas are also equal. Let radius of two circles be `r_1 and r_2` Now, Area of circles are equal So,`pir_1^2=pir_2^2` `rArr r_1^2=r_2^2` `rArr r_1=r_2` So, their radii are equal , so q is also true Now, soppose q is true, i.e., radius of both these circles are equal. When radius of both these circles are equal then they will of same size. So, two circles are of same SHAPE and size which i is the required criteria of congruency. Hence, both circles are congruent. So p is also true. |
|
| 674. |
Differentiate the following with respect to x: x cos x + e^(x) |
|
Answer» |
|
| 675. |
If x^(2) + 6x-27 gt 0, -x^(2) + 3x + 4 lt 0, then x lies in the interval |
|
Answer» `(-OO, -9) CUP (4, oo)` |
|
| 676. |
Which of the following in not true is a-=bx (modm)and x in Z? |
|
Answer» `a + X -=b + x` (MOD m) |
|
| 677. |
int(dx)/((x+1)sqrt(2x^(2)+3x+4)) =K logf(x) + C them |
|
Answer» `K = - (1)/(SQRT(3)), f(x)` |
|
| 678. |
Calculate magnitude of DeltaH in calorie for 1 mol of an ideal gas undergoingadiabatic reversible process from 8 atm, 300 K to 2 atm.(Given : gamma=2, R=2Cal//K//mol) |
|
Answer» <P> SOLUTION :[0600]`(T_(2))/(T_(1))=((P_(1))/(P_(2)))^((1-GAMMA)/(gamma))=((8)/(2))^((1-2)/(2))=((4)/(1))^((-1)/(2))=((4)/(1))^((1)/(2))=(1)/(2)` `T_(2)=150K` `DeltaH=1xx(gammaR)/(gamma-1)(-150)=(2xx2)/(1)xx(-150)=-600` |
|
| 679. |
STATEMENT-1 A,B,C,D are four sets such that n(A cap C)=3 and n(P(A cap C)) ne n(P(B cap D)). STATEMENT-2: If A cup B= A cap B, then it is NOT necessary that A=B. |
|
Answer» |
|
| 680. |
Equation of the tangent at theta=pi//4 to the curve x=a cos2theta,y=2sqrt(2)asintheta is |
|
Answer» `x+y=a` |
|
| 681. |
Show that "tan"^(-1)1/2+"tan"^(-1)2/11="tan"^(-1)3/4 |
|
Answer» |
|
| 683. |
Findthe areaboundedby thecurvey= sqrt(x), x= 2 y+3 in thefirstquadrantandY- axis |
|
Answer» |
|
| 684. |
If the eqution of the circle cutting orthogonally the circlesx^(2)+ y^(2) - 6x = 0 , x^(2) + y^(2) + 4x + 3y + 1 = 0and which has its its centre on the line x + 2y = 5 isx^(2) + y^(2) - 2ax - 2by + c = 0then the dessending order of a,b,c is |
| Answer» Answer :A::B | |
| 685. |
Which is the following is a homogeneous differential equation ?a)(4x + 6y + 5)dy - (3y + 2x + 4) dx = 0b) (xy) dx - (x^3 + y^3)dy = 0c)(x^3 + 2y^2)dx + 2xy dy = 0d)y^2 dx + (x^2 - xy - y^2) dy = 0 |
|
Answer» (4x + 6y + 5)DY - (3y + 2x + 4) dx = 0 |
|
| 687. |
Let veca = 2hati+hatj,vecb = -hati+3hatj+hatk and vecc = hati+2hatj+5hatk be three vectors. Find veccxxveca |
Answer» SOLUTION :
|
|
| 688. |
Let us consider one vertex and one side through the vertex along x -axis of a triangle . Now the coordinates of the vertices B,C and A of any triangle ABC (0,0) ,(a,0) and (h,k) respectively should be taken .If the altitude (AE)of the triangle in question (ii) greater than sqrt(10)and the lenght of AB and AC are of integral value , then the lenght of AC is - |
|
Answer» 3 |
|
| 689. |
If z_1=1+2i,z_2=2+3i,z_3=3+4i, " then " z_1,z_2and z_3 represents the vertices of |
|
Answer» EQUILATERAL TRIANGLE |
|
| 690. |
int_(-3pi//2)^(-pi//2)[(x+pi)^(3)+cos^(2)(x+3pi)]dx= |
| Answer» Answer :A | |
| 691. |
A coin is tossed three times. Find the probability of getting at most 2 heads |
|
Answer» `|S|=8` Let B be the event of getting almost 2 heads `thereforeB={HT T,HTH,THH,T TH,THT, HHT, T T T}` `implies |B|=7` `therefore P(B)=|B|/|S|=7/8` |
|
| 692. |
Evalute the following integrals int (1)/((x + 1)sqrt(x - 1)) dx |
|
Answer» |
|
| 693. |
If y=x^2+3x+6 then find triangley and dy when x=10, trianglex=0.01. |
|
Answer» |
|
| 694. |
Fill in the blanks in each of the following, using the answers given against each of them : The slope and x-intercept of the line 3x-y+ k = 0 are equal if k= _____ . |
| Answer» ANSWER :D | |
| 695. |
(x)/(x+1)+(1)/(2)((x)/(x+1))^(2)+(1)/(3)((x)/(x+1))^(3)+....= |
|
Answer» `LOG(1+X)` |
|
| 696. |
Write down the first three terms is the following expansions(1 + x/2)^(-5) |
|
Answer» |
|
| 697. |
Classify 20m//sec^2 measures as scalar and vector. |
| Answer» SOLUTION :The GIVEN MEASURE is a SCALAR. | |
| 698. |
An ellipse with major and minor axis 6sqrt3 and 6 respectively, slides along the coordinates axes and always remains confined in the first quardrant. If the length if arc decribed by center of ellipse is (pilambda)/6 then the value of lambda is |
|
Answer» |
|
| 699. |
Show that the circumcircle of the triangle formed by the lines ax+by+c=0,bx+cy+a=0 and cx+ay+b=0 passes through the origin if (b^(2)+c^(2))(c^(2)+a^(2))(a^(2)+b^(2))=abc(b+c)(c+a)(a+b). |
|
Answer» |
|
| 700. |
Evaluate the following integrals. int(secx)/((secx+tanx)^(n))dx |
|
Answer» |
|