Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 5501. |
The magnetic field between the plates of a capacitor when r gt R is given by: |
|
Answer» `(mu_0I_Dr)/(2piR^2)` |
|
| 5502. |
A wooden cubical block ABCDEFG of mass m and side a is wrapped by a square wire loop of perimeter 4a, carying current I. The whole system is placed at frictionless horizontal surface in a uniform magnetic field vecB=B_0hatj as shown in fig. In this situation, normal force between horizontalsurface and block passes through a point at a distance x from centre. Choose correct statement (s). |
|
Answer» The block must not TOPPLE if `Ilt (mg)/(aB_0)` For rotation equilibrium: `tau=mgx implies Ia^2B_0=mgx` `implies x=(Ia^2B_0)/(mg)` For the block not to topple: `xlta/2 implies Ilt(mg)/(2aB_0)` 
|
|
| 5503. |
When a charged particle enters perpendicular to a magnetic field, it experiences a force. What is the practical application of this effect ? |
| Answer» SOLUTION :CYCLOTRON | |
| 5504. |
De Broglie wavelength of an electron lambda = ___. |
| Answer» SOLUTION :12.270/`sqrtv` `A^@` | |
| 5505. |
When a charged particle enters perpendicular to a magnetic field, it experiences a force. What is the effect of this force on the moving particle? |
| Answer» SOLUTION :The PARTICLE MOVES in a CIRCULAR PATH | |
| 5506. |
A series RCL circuit operating at 60.0 Hz contains a 35 Omega resistor and an 8.2 muF capacitor. If the power factor of the circuit is +1.00, what is the inductance of the inductor in this circuit? |
| Answer» ANSWER :A | |
| 5507. |
A body is projected vertically up with u.Its velocity at half its maximum height is |
|
Answer» `(U)/(2)` |
|
| 5508. |
A concave mirror forms an image of a real object. Which statement is wrong? |
|
Answer» the IMAGE is real |
|
| 5509. |
A tuning fork is in resonance with a closed pipe. But the same tuning fork cannot be in resonance with an open pipe of the same length. Why ? |
| Answer» SOLUTION :For the same LENGTH of air column, and the same speed of sound, the fundamental FREQUENCY of the air column in a closed pipe half that in an open pipe. Hence, a tuning FORK in unison with the air column in a closed pipe cannot be in unison with the air column of the same length in an open pipe. | |
| 5510. |
In Karnatake , the normal domestic power supply AC is 220V, 50 Hz . Here 220 V and 50 Hz refer to |
|
Answer» Peak VALUE of voltage and frequency |
|
| 5511. |
If S={x: x is a positive multiple of 3 less than 100} and P={X:X is a prime number less than 20}. Then, n(S)+n(P) is equal to |
|
Answer» 34 |
|
| 5512. |
For a satellite moving in an orbit around the earth, the ratio of kinetic energy to potential energy is |
|
Answer» Solution :`-(GMM)/(R^(2))+momega^(2)R=0 RARR (GMm)/(R^(2))=momega^(2)R` K.E. `=(1)/(2)I OMEGA^(2)=(1)/(2)m R^(2)omega^(2)=(GMm)/(2R)` P.E. `=-(GMm)/(R )` `:. K.E. =(|P.E.|)/(2):. (K.E.)/(|P.E.|)=(1)/(2)` |
|
| 5513. |
The coil employed in a experiment similar to that of Stewart and Tolman has a diameter d=500 mm and N=400 turns of copper wire. The moment the coil stops it is connected through a pair of sliding contacts to a ballistic galvanometer Fig. The total circuit resistance is R-50 ohm. The coil is rotated at a constant speed of n=6000 r.p.m. and quickly brought to a halt, the charge passing through the galvanometer being Q=1.1xx10^(-8)C. Find the specific charge of the charge carriers in copper. |
|
Answer» |
|
| 5514. |
An n-p-n transistor power amplifier in C.E configuration gives |
|
Answer» VOLTAGE AMPLIFICATION only |
|
| 5515. |
A proton and a alpha particle are accelerated from rest through a potential difference of 100 volt. Find (i) Their KE in eV and Joule (ii) which particle will move faster. |
| Answer» Solution :` (1) 100 EV, 200 eV, 1.6 xx 10 ^(-17) J, 3.2 xx 10 ^(-17) J (II)` Proton | |
| 5516. |
The plates of a parallel plate capacitor with no dielectric are connected to a voltage source. Now a dielectric of dielectric constant K is inserted to fill the whole space between the plates with voltage source remaining connected to the capacitor. |
|
Answer» the energy stored in the capacitor will become K-times |
|
| 5517. |
A ground receiver station is receiving a signal at 100MHz transmitted from a ground transmitter at a height of 300m located at a distance of 1000km. It is coming via |
|
Answer» GROUND wave |
|
| 5518. |
An alpha particle and a proton having same momentum enter into a region of uniform magnetic field and move in circular paths. The ratio of the radii of curvature of their paths, (R_(alpha))/(R_(p)) in the field is |
| Answer» Answer :A | |
| 5519. |
Unit vector(vecA xx vecB)/(abs (vecA xx vecB)) is perpendicular to |
|
Answer» `VECA` |
|
| 5520. |
12 identical wires, each with resistance 24 Omegaare interconnected to form a cube. Find equivalent resistance of this cube across its diagonally opposite points. |
| Answer» SOLUTION :R. = 20 `OMEGA` | |
| 5521. |
When a mirror is rotated through an angletheta,the reflected from it turns through an angle of : |
|
Answer» `THETA` |
|
| 5522. |
In a diode detector, output circuit consist of R=1M ohm, C=1pF.Calculate the carrier frequency it can detect. |
|
Answer» |
|
| 5523. |
The poet stood at the intersection of? |
|
Answer» crossroads |
|
| 5524. |
The equivalent capacitance between A and B for the combination of capacitors shown in figure, where all capacitances are in microfarad is |
|
Answer» `6.0 MUF` |
|
| 5525. |
The wavelength lambda_(e) of an electron and lambda_(P) of a photon of same energy E are related by: |
|
Answer» <P>`lambda_(p)proplambda_(e)^(2)` `lambda_(e)=(h)/(sqrt(2mE))` `therefore lambda_(e)^(2)=(h^(2))/(2mE) thereforeE=(h^(2))/(2mlambda_(e)^(2))` Wavelength of photon, `lambda_(p)=(hc)/(E )=(hc)/((h^(2))/(2mlambdae^(2)))=(2mclambda_(e)^(2))/(h)` `therefore lambda_(p) prop lambda_(2)^(2) [because (2MC)/(h)="constant"]` |
|
| 5526. |
Equation showing relation between angle of polarisation and refractive index is ...... |
|
Answer» `u SIN theta_(p)=1` `:. mu=tan theta_(p)=(1)/(cot theta_(p))` `:. cot theta_(p)=1` |
|
| 5527. |
An air tight cage with are parrot sitting in it is suspended from the spring balance. The parrot starts flying. The reading of the spring balance will |
|
Answer» increase |
|
| 5528. |
Transverse wave nature of light was first proposed by |
|
Answer» Huygen |
|
| 5529. |
Derive an expression for the magnetic field at a point on the axis of a current carrying circulat loop. |
Answer» Solution :Expression for the magnetic field at a point on the axis of a current carrying circular loop :  (1) Consider 'O' is the centre of a circular coil of one turn and radius 'a'. (2) Let P is a point at a distance r from the centre, along the axis of coil. (3) The plane of the coil is `_|_^(r)` to the plane of paper. (4) Consider two ELEMENTS AB and A'B' each of length dl which are diameterically OPPOSITE. (5) Then, the magnetic fields at P due to these two elements will be DB and dB in the direction PM and PN respectively. (6) These directions are `_|_^(r)` to the lines joining the mid-points of the elements with the point P. (7) Resolve these fields into two components parallel `(dB sin theta)` and perpendicular `(dB cos theta)` to the axis of the coil. (8) The `dB cos theta` components cancel one another and `dB sin theta` components are in the same direction and add up due to the symmetric elements of the circular coil. (9) Therefore, the total magnetic field along the axis `= B = int dB sin theta` of the circular coil along PC - (I) (10) The magnetic field at 'P' due to current element of length 'dl' is `'dB' = (mu_(0))/(4pi)(I dl sin phi)/((a^(2)+ x^(2))) = (mu_(0))/(4pi) (I dl)/((a^(2) + r^(2))) - (II) [because phi = 90^(@)]` (11) From equations (I) and (II), `B = int(mu_(0))/(4pi) (I dl)/((a^(2) + r^(2))) sin theta` From `Delta^(l E)` OPE, `sin theta = (a)/(sqrt(a^(2)+r^(2)))` `RARR B = int(mu_(0))/(4pi) (I dl a)/((a^(2)+r^(2))^(3//2)) = (mu_(0) I a)/(4pi(a^(2)+r^(2))^(3//2)) int dl` But `int dl` = circumference of the coil `= 2pi a` `:. B = (mu_(0) I a)/(4pi(a^(2) + r^(2))^(3//2)) xx 2pi a = (mu_(0) I a^(2))/(2(a^(2) + r^(2))^(3//2))` (12) If the coil contains N turns, then `B = (mu_(0) NI a^(2))/(2(a^(2)+r^(2))^(3//2))` (13) AT the centre of the coil `r = 0, B = (mu_(0) NIa^(2))/(2a^(3)) = (mu_(0) NI_(A))/(2pi r^(3))` |
|
| 5530. |
A transformer is having 2100 turns in primary and 4200 turns in secondary. An A.C. source of 120 V, 10 A is connected to its primary, the secondary voltage and current are ……. |
|
Answer» 240 V, 5 A `epsilon_2/epsilon_1=N_2/N_1` `THEREFORE epsilon_2/120=4200/2100` `therefore epsilon_2`= 240 V `I_2/I_1=N_1/N_2` `therefore I_2/10=2100/4200` `therefore I_2`= 5A |
|
| 5531. |
Explain : "Increasing the current sensitivity may not necessarily increase the voltage sensitivity". |
|
Answer» Solution :1. CURRENT sensitivity is given by, `phi/I=(NAB)/k""...(1)` 2. If N `to` 2N that is we double the number of turns, then `phi/I=(2phi)/I` 3. Thus, the current sensitivity doubles. HOWEVER the resistance of the galvanometer is LIKELY to double since it is proportional the length of the wire. 4. Voltage sensitivity, `phi/V=((NAB)/k)(1/V)=((NAB)/k)1/R` If `Nto2NandRto2R` then, voltage sensitivity does not change. `phi/Vto phi/V` 5. So, it is not NECESSARY to change in voltage sensitivity by changing current sensitivity. |
|
| 5532. |
If alpha-current gain of a transistor is 0.98 . What is thevalue of beta-current gain of the transistor ? |
|
Answer» 0.49 |
|
| 5533. |
A fusion reaction is much more energetic than a fission reaction. Comment. |
| Answer» Solution :True, This is because energy released PER unit mass of FUEL is MUCH HIGHER in fusion than in FISSION. | |
| 5534. |
The most important point of Huygen's wave theory is that ...... |
|
Answer» it is APPLICABLE only to MECHANICAL WAVES |
|
| 5535. |
There is a uniform magnetic field B normal to the xy plane. A conductor ABC has length AB=l_(1), parallel to the x-axis, and length BC=l_(2), parallel to the y-axis. ABC moves in the xy plane with velocity v_(x)hat(i)+v_(y)hat(j). The potential difference between A and C is proportional to |
|
Answer» `v_(x)l_(1)+v_(y)l_(2)` 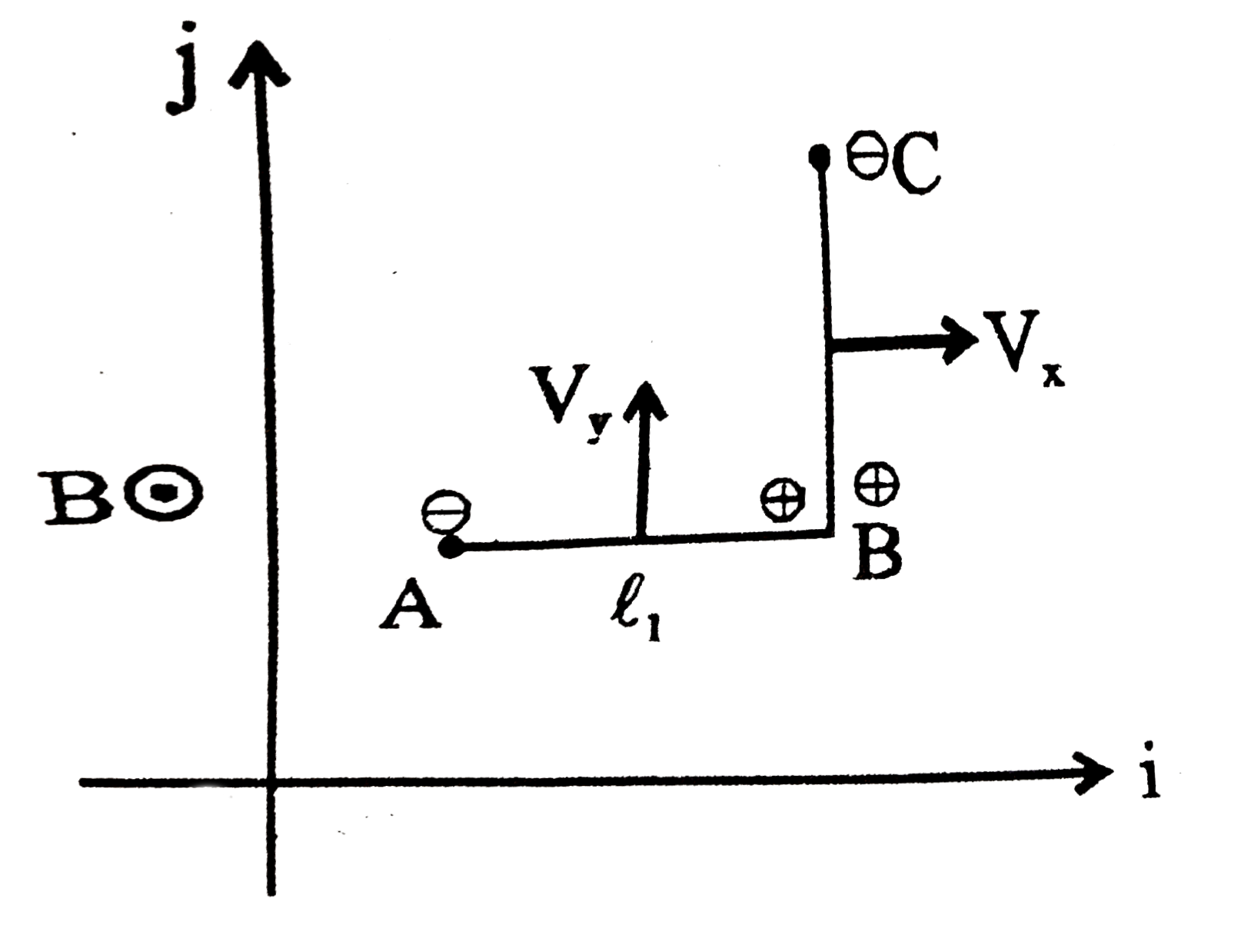 `V_(A)-V_(C )=BV_(x)l_(2)-BV_(y)l_(1)` `V_(A)-V_(C )=B(V_(x)l_(2)-V_(y)l_(1))` |
|
| 5536. |
A charged particle carrying chargeq=1 mu C moves in uniform magnetic field with velocity v_1 = 10^6 m/s at angle45^0 with x - axis in x -y plane and experiences a force F_1 = 5 sqrt(2) m N along the negative z-axis . Wen the same particle move with velocity v_2= 10^6 m/s along the z-axis it experiences a force F_2 in y - direction. Find (a) the magnitude and direction of the magnetic field (b) the magnitude of the force F_2. |
|
Answer» Solution :`F_2` is in y-direction when velocity is along z-axis Therefore, MAGNETIC field should be along x-axis. So let , `vec B = B_0 hati` a) Given `vec(V_1) = (10^6)/(sqrt(2)) hat i + (10^6)/(sqrt(2)) hat J` and `vec F_1 = - 5 sqrt(2) XX 10^(-3) hatk` From the equation, `vec F = Q(vec v xx vec B)` we have `(-5 sqrt(2) xx 10^(-3)) hat k = (10^(-6))[(10^6/sqrt(2) hat i + (10^6)/(sqrt(2)) hat j) xx (B_0 hat i) ] = - (B_0)/(sqrt(2)) hatk` `therefore (B_0)/(sqrt(2)) = 5sqrt(2) xx 10^(-3) or B_0 = 10^(-2)T` Therefore , the magneticfield is , `vec B = (10^(-2) hati) T` `b) F_2 = B_0 qv_2 " sin " 90^@` as the angle between `vecB` and `vecv` in this case is `90^@` `therefore F_2 = (10^(-2))(10^(-6))(10^6) = 10^(-2)N` |
|
| 5537. |
On what principle is an electron microscope based ? |
| Answer» Solution :As electron microscope exploits the wave NATURE of an accelerated beam of ELECTRONS (having a very small WAVELENGTH) to provide high magnifying and resolving powers. | |
| 5538. |
Using the Fresnel equations, find: (a) the reflection coefficient of natural light falling normally on the surface of glass, (b) the relative loss of luminous flux due to reflections of a paraxial ray of natural light passing through an aligned aoptical system comprising five glass lenses (secondary reflections o flight are to be neglected). |
|
Answer» Solution :We decompose the natural light into two components with intensity `I_(||) = (1)/(2)I_(0) = I_(bot)` where `||` has its electirc vector OSCILLATING parallel to the PLANE of incidence and `bot` has the same `bor^(r )` to it. By Frensel's equations for normal incidence `(I'_(bot))/(I_(bot)) = underset(theta_(1)rarr0)lim (sin^(2)(theta_(1) - theta_(2)))/(sin^(2)(theta_(1) + theta_(2))) = underset(theta_(1)rarr0)lim ((theta_(1) - theta_(2))/(theta_(1) + theta_(2)))^(2) = ((n - 1)/(n + 1))^(2) = rho` similarly `(I'_(||))/(I_(||)) = rho = ((n - 1)/(n + 1))^(2)` Thus `(I')/(I) = rho = ((0.5)/(2.5))(2) = (1)/(25) = 0.04` (b) The REFLECTED light at the first surface has the intensity `I_(1) = rhoI_(0)` Then the transmitted light has the intensity `I_(2) = (1-rho)I_(0)` At the second surface where light emerges form glass inot air, the reflection coefficient is again `rho` because `rho` is invariant under the subsitution `n rarr (1)/(n)`. Thus `I_(3) = rho(1 - rho)I_(0)` and `I_(4) = (1 - rho)^(2) I_(0)`. For `N` lenses the loss in luminous FLUX is then `(Delta Phi)/(Phi) = 1- (1- rho)^(2N) = 0.335` for `N = 5` 
|
|
| 5539. |
Resistance of a wire at temperature t^(@)C is R=R_(0)(1+at+bt^(2)) Here, R_(0) is the temperature at 0^(@)C. Find the temperature coefficient of resistance at temperature t is |
|
Answer» SOLUTION :`alpha=(1)/(R ).(dR)/(DT)=(1)/(R_(0)(1+at+bt^(2)))[R_(0)(a+2bt)]` `THEREFORE alpha=((a+2bt)/(1+at+bt^(2)))` |
|
| 5540. |
Frequency for maximum energy radiation of ideal black body at temperture T is U_m. If Wein’s constant is b and velocity of heat radiation in vacuum is c then – |
|
Answer» `U_m = b//T` |
|
| 5541. |
Find the equivalent resistance of the network shown in figure between point A and B when the p-n junction diode is ideal and: (i) A is at higher potential. (ii) B is at higher potential |
|
Answer» Solution :Equivalent RESISTANCE is (i) `10 Omega`, As DIODE is FORWARD biased. (II) `20 Omega`, diode is reverse biased. |
|
| 5542. |
Derive the formula expressing molar heat capacity of a unidimensional crystal, a chain of identical atoms, as a function of temperature T if the Debye temperature of the chain is equal ot Theta. Simplyfie the octained expression for the case Tgt Theta |
|
Answer» Solution :In the DEBYE approximation the number of modes per unit FREQUENCY interval is given by `dN= (1)/(pi v)d omega 0 LE omega le(k Theta)/(ħ)` But `(k Theta)/(ħ)= pin_(0)v` Thus `dN=(l)/(pi v)d omega, 0 le omega le pin_(0)v` The enrgy per mode is `lt E ge(1)/(2)ħ omega+(ħ omega)/(e^(ħ omega//KT)-1)` The total interval energy of the chain is `U=(l)/(pi v) int_(0)^(pin_(0)v) (1)/(2)ħ omega d omega` `+(l)/(piv)int_(0)^(pi n_(0)v)( ħ omega)/(e^( ħ omega//kT)-1) domega=(l ħ)/(4pi v)(pi n_(0)v)^(2)+(l ħ)/(4 pi v)(pi n_(0)v)^(2)+(l)/(pi v ħ)(kT)^(2) int_(0)^(Theta//T)(xdx)/(e^(x)-1)= ln_(0)k.( ħ)/(k)(pi n_(0)v).(1)/(4)` `+ln_(0)k(T^(2))/((pi n_(0)vħ//k)) int_(0)^(Theta//T)(x dx)/(e^(x)-1)` We put `ln_(0)k=R` for `1` mole of the chain Then `U=R Theta{(1)/(4)+((I)/(Theta))^(2) int_(0)^(Theta//T)(x dx)/(e^(x)-1)}` Hence the molar heat capacity is by defferentiation `C_(v)=((delU)/(delT))=R[2((T)/(Theta))int_(0)^(Theta//T)(xdx)/(e^(x)-1)-(Theta//T)/(e^(e//T)-1)]` when `T GT gt Theta, C_(v)~~R` |
|
| 5543. |
One end of a massless spring of spring constant 100 N/m and natural 0.5 m is fixed and the other end is connected to a particle of mass 0.5 kg lying on a frictionless horizontal table. The spring remains horizontal. If the mass is made to rotate at an angular velocity of 2 rad/s, find the elongation of the spring. |
|
Answer» Solution :The restoring FORCE in the spring provides the centripetal force to the mass. If .x. is the EXTENSION in the spring, then `Kx=m(L+x)omega^(2)` Putting the VALUES, we get `x=(0.5xx4xx0.5)/(100-0.5xx4)` `x=1 CM` |
|
| 5544. |
What is an expression for instantaneous value of an AC. |
|
Answer» SOLUTION :`I = I_0` sin wt. where I = INSTANTANEOUS value of AC. `I_0`= Peak value of AC `omega` = Angular FREQUENCY |
|
| 5545. |
निम्नलिखित में परिमेय संख्या ज्ञात कीजिए : |
|
Answer» `piऔर 22/7` दोनों परिमेय हैं |
|
| 5546. |
Angle (in rad) made by the vector sqrt(3)hati+hatj with the x-axis is |
|
Answer» `pi//6` |
|
| 5547. |
Almost all of naturally occurring uranium is ._92^238U with a half-life of 4.468xx10^9 yr. Most of the rest of natural uranium is ._92^235U with a half-life of 7.038xx10^8 yr.Today a sample contains 0.72% ._92^235U (a)What was this percentage 1.0 billion years ago ? (b)What percentage of the sample would be ._92^235U in 100 million years ? |
|
Answer» |
|
| 5548. |
How does the neutron - proton ratio change (increase, decrease or remains the same) during beta - decay? |
| Answer» SOLUTION :n/p RATIO DECREASES because in `BETA-`DECAY a neutron converts into proton. | |
| 5549. |
If the frequency of the input signal is f. What will be the frequency of the pulsating output signal in case of: (i) Half wave rectifier? (ii) full wave rectifier? |
| Answer» SOLUTION :Frequency of output in HALF WAVE rectifier is f and in FULL have rectifier is 2F. | |
| 5550. |
Monochromatic light of frequency 5 times 10^12 Hz travelling in vaccum enters a medium at refractive Index 15 Its wavelength in medium will be |
|
Answer» 5500A |
|