Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 5451. |
Standing waves are produced in a 10 m long stretched string. If the string vibrates in 5 segments and the wave velocity is 20 m/s, the frequency is : |
|
Answer» 2 Hz `= (10)/(5) ` = 2M `therefore (lambda)/(2) = 2m or lambda = 4m` v = 20 `ms^(-1)` `therefore n = (v)/(lambda)= (20)/(4) ` = 5 Hz. CORRECT choice is (C). |
|
| 5452. |
The radius of the smallest electron orbit in the hydrogen like atom is (0.51xx10^(-10))/4 m, then it is : |
|
Answer» HYDROGEN ATOM <BR>`He^(+)` |
|
| 5453. |
Use Gauss's law to show that due to uniformly charged spherical shell of radius R, the electric field at any point situated outside the shell at a distance r from its centre is equal to the electric field at the same point, when the entire charge on the shell were concentrated at its centre. Also plot the graph showing the variation of electric field with r, for r le R and r ge R. |
Answer» Solution :Consider a UNIFORMLY charged thin spherical shell of radius R and having a charge Q. To find electric field at a point P outside the shell situated at a distance `r(r gt R)` from the CENTRE of shell, consider a sphere of radius r as the Gaussian SURFACE. All points on this surface are equivalent relative to GIVEN charged shell and, thus, electric field `vecE` at all points of Gaussian surface has same magnitude `vecE` and `hatn` are parallel to each other.  `therefore ` Total electric flux over the Gaussian surface `phi_(E )= int vecE. hatn ds=E.4pi r^(2)"" ...(i)` According to Gauss.s theorem, `phi_(E )=(1)/(in_(0))"(charge enclosed)"=(Q)/(in_(0))"" ...(ii)` Comparing (i) and (ii), we get `E.4pi r^(2)=(Q)/(in_(0)) or E=(Q)/(4pi in_(0)r^(2))`. Thus, for any point outside the shell, the effect is, as if whole charge Q is concentrated at the centre of the spherical shell. A graph showing the variation of electric field E with r has been plotted here. 
|
|
| 5454. |
Whom we call element and compounds/mixtures. |
| Answer» Solution :Atoms containing ONE KIND are elements and containing more than one kind are COMPOUNDS. | |
| 5455. |
The frequency response curve (as shown in figure below) for the filter circuit used for production of AMwave should be |
|
Answer» i followed by II `2omega_(m)=(omega_(C)+omega_(m))-(omega_(c)-omega_(m))` it is applicable for case (i),(ii) and (iii) The (iv) will reject the REQUIRED SIGNAL for AM waves. |
|
| 5456. |
When a certain circuit consisting of a constant e.m.f. E an inductance L and a resistance R is closed, the current in, it increases with time according to curve 1. After one parameter ( E , L or R ) is changed, the increase in current follows curve 2 when the circuit is closed second time. Which parameter was changed and in what direction |
|
Answer» L is INCREASED |
|
| 5457. |
A body in motion along a straight line. From position time graph Calculate it'sTime for which the body is moving away from origin. |
| Answer» Solution :(IV) Body moves towards the origin CD Total TIME `30-20` = 10 seconds. | |
| 5458. |
A straight wire of length L is bent into a semicircular loop. Use Biot-Savart's to deduce an expression for the magnetic field at its centre due to the curretn I passing through it. |
|
Answer» Solution :As shown in FIG. consider a wire of length L bent into a semicular loop of radius `R (R = L/(pi))`. Let a current I flows through it. To calculate magnetic field at centre O of the loop, Let us consider a small curretn Idl. Then as per Biot-Savart.s law `dB = (mu_0)/(4PI) (I dl sin theta)/(R^2)= (mu_0)/(4 pi) (I dl sin 90^@)/(R^2) = (mu_0 I dl)/(4 pi R^2)` `:.` Total magnetic field at point O due to entire wire `B = (mu_0 I)/(4 pi R^2) sum dl = (mu_0 I)/(4 pi R^2) cdot pi R = (mu_0 I)/(4 R) = (mu_0 pi I)/(4L)` 
|
|
| 5459. |
What is magnetic dipole moment ? |
|
Answer» Solution :If a magnetic dipole consists of a north POLE of strength (+m) and south pole of strength (-m) and the DISTANCE between the TWO poles is 2l, then magnetic dipole moment is given by M=2L m. |
|
| 5460. |
Two metal spheres A and B of radii a & b (a lt b) respectively are at a large distance apart. Each sphere carries a charge of 100muO. the sphere are connected by a conducting wire, then |
|
Answer» Charge will FLOW from A to B |
|
| 5461. |
What is meant by critical mass in a nuclear chain reaction? |
| Answer» Solution :Critical MASS in a nuclear chain reaction is the minimum mass of FISSIONABLE material that WOULD sustain the nuclear chain reaction at a steady rate. The neutron reproduction factor K, in this CASE, becomes equal to one i.e., rate of production of NEUTRONS is just equal to the rate of loss of neutrons. | |
| 5462. |
Which of the following phenomena support the wave theory of light? (1)Scattering (2) Interference (3) Diffraction (4) Velocity of light in a denser medium is less thanthe velocity of light in the rare medium : |
|
Answer» 1, 2 and 3 |
|
| 5463. |
A gas is a mixture of two parts by volume of hydrogen and one part by volume of nitrogen. If the velocity of sound in hydrogen at 0°C is 1300 m/s. The velocity of sound in the gaseous mixture at 27^(@) Cis 325sqrt(x)m//s. Find x |
|
Answer» |
|
| 5464. |
Determine the 'effective focal length' of the combination of two lenses of focal lengths 30cm and -20 cm if they are placed 8.0 cm apart with their principal axes coincident. Does the answer depend on which side a beam of parallel light is incident ? Is the notion of effective focal length of this system useful at all ? (b) An object .15 cm in size is placed on the side of the convex lens in the above arrangement. The distance between the object and convex lens is 40 cm. Determine the magnification produced by the two lwns system and size of image. |
|
Answer» Solution :(a) Here, `f_(1) = 30 cm, f_(2) = - 20 cm, d = 8.0 cm, f = ?` Let a parallel beam be incident on the convex lens first. If 2nd lens were absent, then `:.u_(1) = oo` and `f_(1) = 30 cm` As `(1)/(v_(1)) - (1)/(u_(1)) = (1)/(f_(1)):.(1)/(v_(1)) - (1)/(oo) = (1)/(30) or v_(1) = 30 cm` This image would now act as a virtual object for 2nd lens. `:. u_(2) = + (30 - 8) = + 22 cm, v_(2) = ? f_(2) = - 20 cm` As `(1)/(v_(2)) = (1)/(f_(2)) + (1)/(u_(2)):. (1)/(v_(2)) = (1)/(-20) + (1)/(22) = (-11 + 10)/(220) = (-1)/(220)` `v_(2) = - 220 cm` `:.` Parallel incident beam would appearto diverge from a point `220 - 4 = 216 cm` from the centre of the TWO lens system. (ii) SUPPOSE a parallel beam of light from the left is incident first on the CONCAVE lens. `:.u_(1) = -oo, f_(1) = - 20cm, v_(1) = ?` As `(1)/(v_(1)) - (1)/(u_(1)) = (1)/(f_(1)):.(1)/(v_(1)) = (1)/(f_(1)) + (1)/(u_(1)) = (1)/(-20) + (1)/(- oo) = (-1)/(20)` This image acts as a real object for the 2nd lens `u_(2) = -(20 + 8) = - 28cm, f_(2) = 30cm, v_(2) = ?` As`(1)/(v_(2)) - (1)/(u_(2)) = (1)/(f_(2)):.(1)/(v_(2)) = (1)/(f_(2)) + (1)/(u_(2)) = (1)/(30) - (1)/(28) = (14 - 15)/(420)` `v_(2) = - 420 cm` `:.` The parallel beam appears to diverge from a point `420 - 4 = 416 cm`, on the left of the centre of the two lens system. From the above discussion, we observe that the answer depends on which side of the lens system the parallel beam is incident. THEREFORE, the notion of effective focal length does not seem to be useful here. (b) Here, `h_(1) = 1.5 cm, u_(1) = - 40 cm, m = ? h_(2) = ?` For the 1ST lens, `(1)/(v_(1)) - (1)/(u_(1)) = (1)/(f_(1))` `(1)/(v_(1)) = (1)/(f_(1)) + (1)/(u_(1)) = (1)/(30) - (1)/(40) = (4 - 3)/(120) = (1)/(120)` `v_(1) = 120 cm`. Magnitude of magnification produced by first lens, `m_(1) = (v_(1))/(u_(1)) = (120)/(40) = 3` The image formed by a 1st lens acts as virtual object for the 2nd lens `:. u_(2) = 120 - 8 = 112 cm, f_(2) = - 20 cm, v_(2) = ?` As `(1)/(v_(2)) - (1)/(u_(2)) = (1)/(f_(2)):. (1)/(v_(2)) = (1)/(f_(2)) + (1)/(u_(2)) = (1)/(-20) + (1)/(112) = (-112 + 20)/(112 xx 20) = (- 92)/(112 xx 20)` `v_(2) = (-112 xx 20)/(92)` Magnitude of magnification produced by second lens `m_(2) = (v_(2))/(u_(2)) = (112 xx 20)/(92 xx 112) = (20)/(92)` Net magnification produced by the combination `m = m_(1) xx m_(2) = 3 xx (20)/(92) = (60)/(92) = 0.652` `:.` Size of image, `h_(2) = mh_(1) = 0.652 xx 1.5 = 0.98 cm` |
|
| 5465. |
(a) State the working principle of a potentiometer. With the help of the circuit diagram, explain how a potentiometer is used to compare the emfs of two primary cells. Obtain the requiredexpression used for comparing the emfs.(b) Write two possible causes for one sided deflection in a potentiometer experiment. |
| Answer» Solution :(b) Two possible causes for ONE sided deflection in a potentiometer EXPERIMENT are :1. Positive terminal of PRIMARY cell source e is not connected to point A, where positive terminal of DRIVER cell (battery) has been connected.2. Emf of driver battery is LESS than the unknown emf `epsi` | |
| 5466. |
A particle of mass 3 m at rest decay Into two particles of masses m and 2m having non-zero velocities. What is the ratio of the de-Broglie wavelengths of the particle (lambda_(1)//lambda_(2)). |
|
Answer» 1:1 `lambda=h//p``therefore``lambda_(1)//lambda_(2)=1` |
|
| 5467. |
Over a solenoid of 50cm length and 2cm radius and having 500turns is would another wire of 50 turns near the centre. Calculate (i) mutual inductance of the two coils (ii) Induced emf in the second coil when the current in the primary changes from 0 to 5A in 0.02 sec. |
| Answer» SOLUTION :(i) `78.88muH`, (II) 19.72mV | |
| 5468. |
The resistivity of a material depends on____and ____ |
| Answer» Solution :number DENSITY of ELECTRONS, relaxation TIME | |
| 5469. |
A particle moves in the xy - plane with velocity v = xhati+ythatj. At t = (xsqrt(3))/(y) the magnitudes of tangential and normal accelerations respectively are |
|
Answer» `(sqrt(3Y))/(2),(y)/(2)` So`|v|=v=sqrt(x^(2)+y^(2)t^(2))` Magnitude of tangential acceleration is `a_(t)=(dv)/(DT)=(0+2ty^(2))/(2sqrt(x^(2)+y^(2)t^(2)))` or `a_(t)=(ty^(2))/(sqrt(x^(2)+y^(2)t^(2)))` Now substituting `t=(xsqrt(3))/(y)` we get `((xsqrt(3))/(y)xxy^(2))/(sqrt(x^(2)+y^(2)xx((x^(2)xx3)/(y^(2)))))` `implies a_(t)=(sqrt(3y))/(2)` Also total acceleration of particle is a `=(dv)/(dt)` `implies a=(d)/(dt)(xhati+yt hatj)` `implies a=yhatj` or magnitude of total acceleration is `a=|a|=y` Hence normal acceleration is `a_(n)=a_("total")-a_("tangential ")` So `a_(n)=|a_(n)|=` magnitude of normal acceleration `=sqrt(a^(2)-a_(1)^(2))=sqrt(y^(2)-((y^(4)y^(2))/(x^(2)+y^(2)t^(2))))` `=sqrt((x^(2)y^(2))/(x^(2)+y^(2)t^(2)))=(xy)/(sqrt(x^(2)+y^(2)t^(2))` Now with t `=(xsqrt(3))/(y)` we get `a_(n)=|a_(n)|=(xy)/(sqrt(x^(2)+y^(2).(3x^(2))/(y^(2))))=(xy)/(2x)=(y)/(2)` |
|
| 5470. |
For given metal work function is W_(0) and threshold wavelength is lambda_(0).If metal has work function (W_(0))/(2) then what will be threshold wavelength ? |
|
Answer» `(lambda_(0))/(4)` `THEREFORE (W_(0))/(W_(0))=(lambda_(0))/(lambda_(0))` `(W_(0))/(W_(0))=(lambda_(0))/(lambda_(0))` `(W_(0))/((W_(0))//(2))=(lambda_(0))/(lambda_(0)) [because W_(0)=(W_(0))/(2)]` `therefore 2lambda_(0)=lambda_(0)` |
|
| 5471. |
White light is split into a spectrum by a prism and it is seen on a screen. If we put another indentical inverted prism behind it in contact, what will be seen on the screen ? |
|
Answer» VIOLET will APPEAR where red was |
|
| 5472. |
A monochromatic light of wavelength lamda falls on a single slit. The first secondary maximum occurs at 30^(@) if the width of the slit is equal to |
|
Answer» `(LAMDA)/(2)` |
|
| 5473. |
Is the steady electric current the only source of magnetic field ? Justify your answer. |
| Answer» Solution :No, a VARYING current and a current INDUCED due to electromagnetic induction may also produce a magnetic field. | |
| 5474. |
The binding energy of a satellite of mass 50 kg in a circular orbit around the earth at a height of 600 km above the earth’s surface is |
|
Answer» a)itsK.E.is2500J |
|
| 5475. |
If' muscle times speed equals power' what will be dimensional formulae for muscle ? |
|
Answer» `MLT^-2` |
|
| 5476. |
The resultant of two forces acting at an angle of 120° is 10 kg wt and is perpendicular to one of the forces. That force is : |
|
Answer» `10sqrt(3)`KG wt 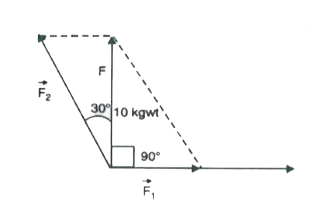 `:.F_(2)COS30^@=F` `F_(2)10/(cos30^@)=(10xx2)/sqrt(3)=20/sqrt(3)kg wt` Also `F_(2)sin30^@=F_(1)` `:.F_(1)=20/sqrt(3)xx1/2=10/sqrt(3)` |
|
| 5477. |
Kirchhoff.s junction rule is a reflection of |
|
Answer» Conservation of MOMENTUM |
|
| 5478. |
Transmission via sky waves is impossible for the frequencies |
|
Answer» LESS than 40MHz |
|
| 5479. |
Explain the phenomenon of hysteresis in magnetic materials. |
|
Answer» Solution :A complete cycle of magnetisation [i.e, graph between magnetisation M (or total magnetic field B developed in the sample) of the sample and magnetising INTENSITY H] for a given ferromagnetic material (say steel) is being shown in Fig. The curve obtained is called hysteresis curve. From this graph, we draw following conclusions: (i) Initiallyas `vecH` is raised from its zero value `vecB` also RISES from zero toa s saturation value `vecB_m` and it is being represented by the curve. OA . But the curve OA does not retrace itself as `vecH` is reduced . `vecB_m` is called "magnetic saturation" of the given sample . (iii) As `vecH` is reduced, the curve is along AB. Point B indicates the value of magnetic field B left behind even when `vecH` is reduced to zero. This value of field `vecB` , (given by OB) is called .RESIDUAL magnetism. or .retentivity. or .remanence.. 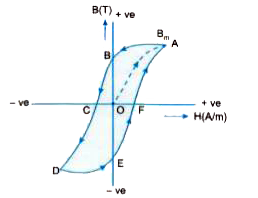 (iii) To reduce `vecB` to zero we have to increase value of `vecH` in the REVERSE direction. In figure point C represents the state of `vecB` =0 . Value of `vecH` corresponding to point C i.e. `vecH_C` is known as .coercive force. or .coercivity.. (iv) No segment OA, AB, BC, CD ... etc., of the curve is linear. It means that `vecB` is not directly PROPORTIONAL to `vecH` over any appreciable range. (v) Lagging behind of `vecB` as compared as `vecH` is known as the .Hysteresis. and the magnetisation cycle curve is known as thehysteresis curve. (iv) The area within the B-H loop represents the energy dissipated per unit volume per cycle in the material. |
|
| 5480. |
In an experiment to measure emf epsilon_(1) of a battery by a potentionmeter , the main circuituses a battery of emf epsilon_(2) . Then. |
|
Answer» `epsilon_(1) = epsilon_(2)` |
|
| 5481. |
Photoelectric emission rate is a direct function of radiation : |
|
Answer» frequency |
|
| 5482. |
When two capacitors charged to different potentialsare connected by a conducting wire, what is not true ? |
|
Answer» CHARGE LOST by one is EQUAL to charge gained by the other |
|
| 5483. |
(a) Three resistors 3Omega, 4Omega, and 12Omega are connected in parallel. What is the effective resistance of the combination? (b) If the combination is connected to a battery of emf 6V and internal resistance 0.5Omega, find the current drawn from the battery and terminal potential difference across the battery. |
|
Answer» Solution :Let `R_(1)= 3OMEGA, R_(2)= 4Omega " &" R_(3)=12Omega` are three resistances of the resistors. Effective resistance in parallel `(1)/(R_(P))= (1)/(R_(1)) + (1)/(R_(2)) + (1)/(R_(3))` `(1)/(R_(P))= (1)/(3) + (1)/(4) + (1)/(12)= (96)/(144)` `R_(P)= 1.5Omega` Current DRAWN `I= (E )/(R + r) = (6)/(1.5 + 0.5)= 3A` `V= IR_(P) = 3 Omega xx 1.5A= 4.5V` |
|
| 5484. |
What do you understand by figure of merit ? |
|
Answer» SOLUTION :Figure of merit is defined as the current required per division of deflection derivation `K = (1)/(theta)`, SI unit A/div in observation for half deflection METHOD `i_(G) = Ktheta, i_(g) = (E )/(R+G)` `k=(1)/(theta) [ (E )/(R+G)]` It enables us to FIND current required for full scale deflection. |
|
| 5485. |
The figure shows hysteresis curves for soft iron and steel. Point out the wrong statement about the magnetic properties of soft iron and steel |
|
Answer» a) retentivity of soft iron is LESS than steel |
|
| 5486. |
Show graphically, the variation of the de-Broglie wavelength (lamda) with the potential (V) through which an electron is accelerated from rest. |
|
Answer» Solution :Ad de-Broglie wavelength `lamda` of an electron accelerated with a POTENTIAL of V is GIVEN by: `lamda=(h)/(sqrt(2emV))`, HENCE `lamda-V` graph is shown in figure 
|
|
| 5487. |
The diameter ofa sphere is 4.24 m. Calculate its surface area with due regard to significant figures . |
|
Answer» Solution :Diameter d=4. 24 m Radius r `=(d)/(2) = (4.24)/(2) = 2.12` surface AREA of SPHERE = `4pi r^(2)` `= 4xx3.1428xx2.12xx2.12` In the above multiplication 2.12 has 3 significant figures. Hence 3.1428 is rounded off to have 3 + 1 =4 significant figures. It BECOMES 3.143. Surface area `=4xx3.143xx2.12xx2.12=56.50` 56.50 this to be rounded off to have 3 significant figures. `:. `Area is `56.5m^(2)` |
|
| 5489. |
The shortest wavelength of the spectrum line is that of electron being transits into atom to ion from n = 2 to n = 1 for ....... |
|
Answer» hydrogen atom `(1)/(lamda)=RZ^(2)[(1)/(n_(f)^(2))-(1)/(n_(i)^(2))]` R and `(1)/(n_(f)^(2))-(1)/(n_(f)^(2))` are constant `:.(1)/(lamda)propZ^(2)` and Z = 3 is maximum for doubly ionized lithium in a given atom. |
|
| 5491. |
Lens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as : P=(1)/(f)=(n-1)((1)/(R_(1))-(1)/(R_(2))) where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R_(1) and R_(2) are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R_(1) and R_(2) with their proper signs as per sign convention being followed by us. Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R_(1)|=|R_(2)|=R" (say)" How is result of part (d) modified if two parts are placed together as shown in Fig. (c)(ii)? |
|
Answer» Solution :HOWEVER, in the arrangment shown in figure (c) (II), the So the combination will BEHAVE as a PLANE GLASS plate. |
|
| 5492. |
A disc of radius a and mass m rests between two light rods, which are smoothly hinged together at point O with their ends A and B resting on a smooth table and are maintained in equilibrium by string AB as shown in the figure. Choose the correct option(s). |
|
Answer» The magnitude of NORMAL force acting on the rod at point `A` is `(mg)/(2)` `F_(e)=lambdaErArr` electric force `=lambda(2lambda)/(4piepsilon_(0)l)=(lambda^(2))/(2piepsilon_(0)l)` `lambdarArr` excess charge per unit length of wire `F_(m)rArr (mu_(0)l^(2))/(2pil)rArr` magnetic force According to given QUESTION `F_(@)=F_(m)` `(lambda^(2))/(2piepsilon_(0)l)=(mu_(0)I^(2))/(2pil)` `rArr ((1)/(lambda))^(2)=(1)/(epsilon_(0)mu_(0))` `rArr((ln20)/(piepsilon_(0)V)xx(V)/(R ))^(2)=(1)/(mu_(0)epsilon_(0))` `rArr R=sqrt((mu_(0))/(epsilon_(0)))((ln20)/(pi))=360Omega` 
|
|
| 5493. |
In a plane electromagnetic wave, the electric field oscillates sinusoidally at a frequency of 2.0xx10^(10) Hz and amplitude 48 V m^(-1). What is the wavelength of the wave ? |
|
Answer» SOLUTION :(a) `lamda =(c//v) =1.5 xx10^(-2) m` (B) `B_(0)=(E_(0)//c)=1.6 xx10^(-7) T` (c ) Energy density in E field: `u_(E) =(1//2)epsi_(0) E^(2)` USING `E= cB, and c=(1)/(sqrt(mu_(0) epsi_(0)), u_(E)=u_(B)` |
|
| 5494. |
Lens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as : P=(1)/(f)=(n-1)((1)/(R_(1))-(1)/(R_(2))) where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R_(1) and R_(2) are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R_(1) and R_(2) with their proper signs as per sign convention being followed by us. Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R_(1)|=|R_(2)|=R" (say)" If two lens parts obtained in (b) are joined together as shown in Fig. (c), (i) what is the net power of the combination? |
|
Answer» SOLUTION :When two PARTS cut along SECTION XX. are joined as SHOWN in figure (c) (i), then NET power `=P+P=2P=2xx"power of original biconvex lens"` |
|
| 5495. |
A carrier wave is modulated by a number of sine waves with modulation indices 0.1,0.2,0.3 The totaal modulation index (m) of the wave is |
|
Answer» `0.6` |
|
| 5496. |
A point source is situated at a distance x < f from the pole of the concave mirror of focal length f. At time t = 0, the point source starts moving away from the mirror with constant velocity. Which of the graphs below represents best, variation of image distance | v | with the distance x between the pole of mirror and the source. |
|
Answer»
|
|
| 5497. |
Describe briefly the underlying principle of a transistor amplifier working as an oscillator. Hence, use the necessary circuit diagram to explain how self sustained oscillations are achieved in the oscillator. |
Answer» Solution :A portion of output power is returned at the input in same phase as that of starting power, hence the output in the oscillator gets self sustained. This is termed as POSITIVE FEEDBACK.  As the switch `S_1` is closed, a SURGE of collector current flows through coil `T_2`, which CAUSES a changing magnetic flux around it. Hence a portion of the output is feedback to the coil `T_1` as a RESULT of the positive feedback. The emitter current, therefore, starts oscillating |
|
| 5498. |
If an object's mass and the net force it feels are both known, them newton's second law could be used to directly calculate which quantity? |
|
Answer» Displacement |
|
| 5499. |
(A): Velocity-time graph for an object in uniform motion along a straight path is a straight line parallel to the time axis. (R ):In uniform motion of an object velocity increases as the square of time elapsed. |
|
Answer» |
|
| 5500. |
Define temperature coefficient of resistance . |
|
Answer» SOLUTION :Temperature coefficient of RESISTANCE `(alpha)` : The ratio of the change in resistance per 1 `.^(@)C` RISE in temperature to the resistance at 0 `.^(@)C` is called the temperature coefficient of resistance. `alpha = (R_(i) _ R_(0))/(R_(0)t)` |
|



