Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 951. |
In a p-n junction diode, the current I can be expressed as I=I_(0)"exp"((eV)/(2k_(B)T)-1) where I_(0) is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, k_(B) is the Boltzmann constant (8.6xx10^(-5)eV//K) and T is the absolute temperature. If for a given diode I_(0)=5xx10^(-12)A and T = 300 K, then (a) What will be the forward current at a forward voltage of 0.6 V ? (b) What will be the increase in the current if the voltage across the diode is increased to 0.7 V ? (c ) What is the dynamic resistance? (d) What will be the current if reverse bias voltage changes from 1 V to 2 V ? |
|
Answer» Solution :Current passing through junction diode, `I=I_(0)["exp"((EV)/(k_(B)T))-1]` where `I_(0)=` Reverse saturated current `=5xx10^(-12)A` `T=300K` `k_(B)=8.6xx10^(-5)eVK^(-1)` `=8.6xx10^(-5)xx1.6xx10^(-19)JK^(-1)` `=13.76xx10^(-24)JK^(-1), 1 eV=1.6xx10^(-19)JK^(-1)` (a) When V = 0.6 V then `I=I_(0)["exp"((eV)/(k_(B)T))-1]""...(1)` but `(eV)/(k_(B)T)=(1.6xx10^(-19)xx0.6)/(13.76xx10^(-24)xx300)=0.23255xx10^(2)` `~~23.26` `therefore` From equation (1), `I_(1)=I_(0)["exp"(23.26)-1]A` `=5xx10^(-12)["exp"(23.26)-1]A` `=5xx10^(-12)[e^(23.26)-1]A` `=5xx10^(-12)[log(0.4343xx23.26)-1]A` `=5xx10^(-12)[1.2586xx10^(10)-1]A` Neglecting 1 compare to `1.2586xx10^(10)` `=5xx10^(-12)xx1.2586xx10^(10)A` `therefore I_(1)=0.06293 A` (b) When V = 0.7V then From equation (1), Taking `(eV)/(k_(B)T)=(1.6xx10^(-19)xx0.7)/(13.76xx10^(-24)xx300)=27.13` `I_(2)=I_(0)["exp"((eV)/(k_(B)T))-1]A` `=5xx10^(-12)[27.13log(0.4343)-1]A` `=5xx10^(-12)[6.07xx10^(11)-1]A` Neglecting 1 compare to `6.07xx10^(11)` `=5xx10^(-12)xx6.07xx10^(11)A` `therefore I_(2)=3.035A` `therefore ` Increase in current `DeltaI=I_(2)-I_(1)` `=3.0350-0.06293` `=2.97207A` `~~2.972`A (c ) `DeltaV=0.7-0.6=0.1V` and `DeltaI=2.972A` `therefore` Dynamic variable resistance, `r_(d)=(DeltaV)/(DeltaI)=(0.1)/(2.972)=0.03364Omega` `therefore r_(d)~~0.0336Omega` (d) When voltage varies from 1 V to 2V then current `I_(0)=5xx10^(-12)`A remains constant it SHOWS that in reverse bias the dynamic resistance is infinite. |
|
| 952. |
To make a p-n junction conducting |
|
Answer» the value of FORWARD BIAS should be more than the BARRIER potential. |
|
| 953. |
Consider the following statements A and B and identify the correct answer: A: Germanium is preferred over silicon in construction of Zener diode B: Germanium have high thermal stability |
|
Answer» A and B are TRUE |
|
| 954. |
The horizontal range of a projectile is times of its maximum height. Its angle of projection will be :- |
|
Answer» `45^(@)` but ,`R= 4 sqrt(3 ) H ` `(u^(2) sin2 theta) /(g)= 4 sqrt(3)((u^(2)sin ^(2)theta )/(2g))` ` sin 2 theta= 4 sqrt(3)(sin^(2)theta )/(2)` `2 sintheta cos theta =(4sqrt(3) sin ^(2)theta )/(2)` ` (1)/(sqrt(3))-(sin theta )/(cos theta ) = tan theta ` or`theta = 30^(@)` |
|
| 955. |
Three charges q each are at vertices of equilateral triangle of side r? How much charge should be placed at the centroid so that the system remains in equilibrium? |
Answer» Solution : Due to THREE identical charges kept at three corners of a triangle, null point (E = 0) is formed at centre 0. Let .Q. be the charge placed at centre of triangle then the charge .Q is in equilibrium. For system to be in equilibrium the force on each charge must be zero. Consider the forces on charge at C. Let `F_A, F_B and F_0` . be the forces on the charge at .C. due to the charges at A, B and .O. respectively. `F_A = F_B = 1/(4 pi epsilon_0) (q^2)/(a^2)` Angle between `vec(F_A)`and `vec(F_B) `is `60^@` The magnitude of RESULTANT of `vec(F_A) and vec(F_B) = sqrt(3) XX 1/(4 pi epsilon_0) (q^2)/(a^2)` The direction of resultant is along OC. The force on C due to "Q"is `vec(F_O) = 1/(4 pi epsilon_0) (Qq)/(((a)/(sqrt3))^2) = 3 xx 1/(4 pi epsilon_0) (Qq)/(a^2) ` (along CO) The resultant force on charge at C is Zero. `vec(F) = vec(F_A) + vec(F_B) + vec(F_O) = 0` `sqrt(3) 1/(4 pi epsilon_0) (q^(cancel(2)))/(cancel(r)^2) + (1)/(4 pi epsilon_0) (3Q cancel(q))/(cancel(r)^2) = 0 implies Q = - q/(sqrt(3))` Negative sign indicates that the force `vec(F_O)` . is opposite to the resultant of `vec(F_A)` and `vec(F_B)`. |
|
| 956. |
Five cells, each of emf E, are joined in parallel. The total emf of the combination is |
| Answer» Answer :C | |
| 957. |
A current carrying circular loop of radius 50 mm, made of a very thin wire has inductance 0.26 muH and is placed in the uniform magnetic field 0,5 mT. The plane of the loop is perpendicular to the magnetic field lines. The resistance of loop can be neglected. Now the magnetic field has been turned off. Find the current in the loop (approximately) |
|
Answer» 30Aa |
|
| 958. |
How long can an electric lamp of 100 W be kept glowing by fusion of 2.0 kg of deuterium ? Take the fusion reaction as " "_(1)^(2)H+ " "_(1)^(2)H to " "_(2)^(3)He+n+3.27 MeV. |
|
Answer» Solution :The amount of energy released per ACT of fusion = 3.27 MeV and a fusion required 2 nuclei of `" "_(1)^(2)H`, hence Energy released in 2.0 kg of `" "_(1)^(2)H = (("Number of atoms in 2 kg"))/2 xx ("Energy per act of fusion")=(6.023xx10^(26))/2xx 3.27 MeV =9.85 xx 10^(26) MeV = 15.76 xx 10^(13) J` LET the 100 W bulb run for t s, then total energy consumed is given by 100`xx t = 15.76 xx 10^(13) implies t =15.76xx10^(11)s= (15.76xx10^(11))/(3.154xx10^(7))year = 4.9 xx 10^(4)`year. |
|
| 959. |
A long horizontal rod has a bead which can slide along its length, and initially placed at a distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration a. If the coefficient of friction between the rod and the bead is u, and gravity is neglected, then the time after which the bead starts slipping is : |
|
Answer» `SQRT((MU)/(ALPHA))` |
|
| 960. |
The unit for the amount of work done in moving a unit positive charge in an electric field is |
|
Answer» Joule |
|
| 961. |
What will be ratio (D"/"f) in microscope where, D is the diameter of the aperture and .f. is the focal length of the objective lens? |
| Answer» Answer :C | |
| 962. |
Compare the specific binding energies of tritium and of the light helium isotope. |
|
Answer» |
|
| 963. |
Two cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Omega and 0.3Omegarespectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell. |
|
Answer» Solution :For PARALLEL grouping of two CELLS `epsi_1 = 1.5V , epsi_2 = 2.0 V , r_1 = 0.2 Omega " and " r_2 = 0.3 Omega` Internal resistance of equivalent cell `r_(eq) = (r_1 r_2)/(r_1 + r_2) = (0.2 XX 0.3)/((0.2 + 0.3)) = 0.12 Omega` and EMF of equivalent cell `epsi_(eq) = (epsi_1 r_2 + epsi_2 r_1)/((r_1 + r_2)) = (1.5 xx 0.3 + 2.0 xx 0.2)/((0.2 + 0.3)) = 1.7V` |
|
| 964. |
The maximum displacement of a particle performing S.H.M. from its mean position is |
|
Answer» AMPLITUDE of S.H.M. |
|
| 965. |
A 15.0 mu Fcapacitor is connected to a 220V, 50Hz source. Find the capacitive reactance and the current (rms and peak) in the circuit. If the frequency is doubled, what happens to the capacitive reactance and the current? |
|
Answer» Solution :The capacitive reactance is `X_C = (1)/(2pi v C) = (1)/(2pi (50)(15.0 xx 10^(-6) ) ) = 212 Omega` The rms current is = `I = (V)/(X_C) = 220/212 - 1.04 A` The peak currentis `i_m = sqrt21 = (1.41)(1.04)= 1.47 A` This current OSCILLATES between +1.47A and -1.47 A and is ahead of the VOLTAGE by `pi/2` If the frequency is DOUBLED, the capacitive reactance is HALVED and consequently, the current isdoubled. |
|
| 966. |
A metal plate of radius 20 cm is charged positively to a potential of 6000 volts and placed at a distance of 5 cm from a parallel earth connected plate .Find the total pull between the plates . |
|
Answer» |
|
| 967. |
The power radiated by a star and its mass ma are related by (P)/(P_(0))=((m)/(M_(0)))^(7//2) where P_(0) and M_(0) are power radiated by the Sun and mass of the Sun respectively. Assume that the fraction of mass lost by the star since its birth is alpha(ltlt1). Calculate the age of the star in terms of alpha,M_(0)P and P_(0). |
|
Answer» <P> |
|
| 968. |
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face ? The refractive index of the material of the prism is 1.524. |
|
Answer» Solution :Here, `angleA = 60^(@)` and n = 1.524 For a ray to suffer total internal reflection at the second FACE of the prism `angler_(2) = anglei_( c)` where `i_( c)= sin^(-1) (1/n) = sin^(-1) (1/1.524) = sin^(-1) (0.6526) = 41^(@)` As `angleA = angler_(1)+ r_(2)` Hence, `angler_(1) = angleA - angler_(2) = angleA - anglei_( c) = 60^(@) - 41^(@) = 19^(@)` As `(sin i)/(sin r_(1)) =n`, `therefore ANGLEI = sin^(-1) (0.4962) = 29.75^(@) = 30^(@) =n` |
|
| 969. |
Two chargesQ and -3Q are placed fixed on x-axis separated by a distance 'd' Where should a third charge 2Q be placed such that it will not experience any force? |
|
Answer» SOLUTION :Let CHARGES Q and -3Q be placed at POINT A and Bseparated by a distance d. The third charge 2Q should be placed at point p on extension of LINE BA never the smaller charge of Q at distance x from it. As net FORCE on 2Q charge is zero. ` therefore "" oversetto (F_(F)) =oversetto (F_(A)) +oversetto (F_(B)) =0 or oversetto (F_(A)) = oversetto (F_(B)) ` ` rArr ""(1)/(4 pi in _0) .(Q(2Q))/(x^(2)) =(1)/(4 piin _0)((-3Q)(2Q))/((x+d) ^(2))` ` rArr ""(1)/(x^(2)) =(3)/((x+d)^(2)) rArr x=(d)/((sqrt(3-1)) ) ` 
|
|
| 970. |
What does author want? |
|
Answer» A violence free nation |
|
| 971. |
Out of blue and red light which is deviated more by the prism ?Give reason. |
| Answer» SOLUTION :The DEVIATION produced by a small ANGLED PRISM is given by delta = (mu - 1)A. | |
| 972. |
A rod lies along the x-axis with one end at the origin and the other at x rarr oo. It carries a uniform charge lambda C/m. The electric field at the point x = -a on the axis will be |
|
Answer» `VEC(E) = (LAMBDA)/(4pi epsilon_(0)a)(-hat(i))` |
|
| 973. |
An infinite nonconducting sheet at x = 0 carries a uniform surface charge density sigma. A thin rod of length 2L has a unifrom linear charge density lambda on one half and lambda on the other half. The rod is hinged at its mid point C at x = 2 L and lies in the XOZ plane making an angle alpha with the positive X-axis as shown in figure . The toqure vec(tau) experienced by the rod is (4sigmalambdaL^(2))/(kin_(0)) j sin alpha. The value of K is |
|
Answer» 1 |
|
| 974. |
Effective resistance between A and B in the given circuit is |
|
Answer» r |
|
| 975. |
Velocity of a body executing U.C.M |
|
Answer» CHANGES abruptly |
|
| 976. |
Phase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative. The phase space diagram for simple harmonic motion is a circle cen-tered at the origin.In the figure, the two circles represent the same oscillator but for different initial conditions, and E_(1) for E_(2) are the total mechanical energies respectively. Then |
|
Answer» `E_(1) = sqrt(2)E_(2)` In `2nd` case amplitude of `SHM` is `2a` Total energy `= (1)/(2)K(amplitude)^(2)` `E_(1)/(2)2k(2a)^(2) , E_(1) = 4 E_(2)` Alternative : Linear momentum `P = MV` `= momegasqrt(A^(2) - X^(2))` `rArr P^(2) = m^(2)omega^(2) (A^(2) - x^(2))` `rArr P^(2) + m^(2)omega^(2)x^(2) = m^(2)omega^(2)A^(2)` Equation of circle (smaller) `P^(2) + x^(2) = a^(2) .......(iii)` Comparing `(i)` and `(ii)` Amplitude `A = 2a` and `(momega)^(2) = (1)/(m)` `(1)/(2)momega^(2)(A)^(2)` So energy `E_(1) = (1)/(2) momega^(2) (2a)^(2)` `(1)/(2)(1)/(m)xx(4a^(2))` `= (2a^(2))/(m)` Comparing `(i)` and `(iii)` `(momega)^(2) = 1 rArr momega^(2)A^(2) = (1)/(2) xx (1)/(m)a^(2) = (1)/(2)(a^(2))/(m^(2))(1a^(2))/(2 m)`. So, `(E_(1))/(E_(2)) = 4 rArr E_(1) = 4E_(2)` |
|
| 977. |
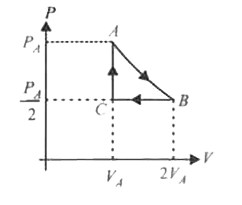
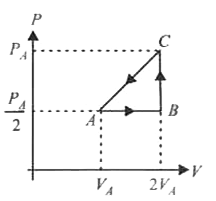
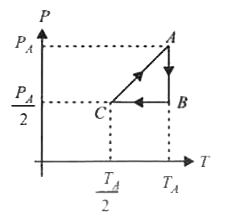
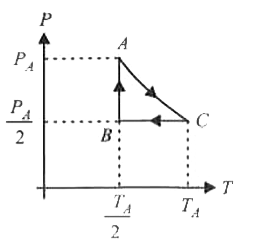
Three moles of an ideal gas C_(p) = 7//2 R at pressure P_(A) and temperature T_(A) is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original volume. Finally the gas is compressed at constant volume to the original pressureP_(A).The correct P-V and P-T diagram indicating the process are |
|
Answer»
I. Isothermal expansion (PV = CONSTANT) at temperature `T_(A)`to twice the initial volume `V_(A)` II. Compression at constant pressure `P_(A)//2` to original volume `V_(A) (i.e., V propto T)` III. Isochoric process (at volume `V_(A)`) to initial conditions `(i.e., P propto T)`. 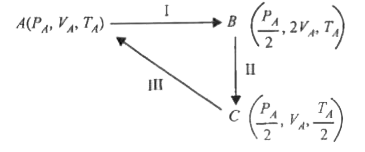
|
|
| 978. |
A river is flowing from west to east at a speed of 5 m/s. A man on the south bank of the river capable of swimming at 10 m/s in a still water wants to swim, across the river in a shortest time. He should swim in a direction |
|
Answer» DUE NORTH |
|
| 979. |
____________are widely used in remote switches of household electronic devices e.g., TV set of AC etc. |
| Answer» SOLUTION :INFRARED | |
| 980. |
A point charge Q is placed at a distance d from the centre of an uncharged conducting sphere of radius R. The potential of the sphere is (d gt R): (Assume potential at infinity to be zero) |
|
Answer» `(1)/(4piepsilon_(0)),(Q)/((d-R))` |
|
| 981. |
The threshold frequency for a certain metal is 3.3xx10^(14)Hz. If light of frequency 8.2xx10^(14)Hz is incident on the metal, predict the cut-off voltage for the photoelectric emission. |
|
Answer» Solution :Here `v_(0)=3.3xx10^(14)Hz and V=8.2xx10^(14)Hz` USING Einstein.s RELATION `h(v-v_(0))=eV_(0)`, we have Cut-off voltage `V_(0)=(h)/(e)(v-v_(0))=(6.63xx10^(-34))/(1.6xx10^(-19))(8.2xx10^(14)-3.3xx10^(14))` `=(6.63xx10^(-34)xx4.9xx10^(14))/(1.6xx10^(-19))=2.0V`. |
|
| 982. |
ABC is an isosceles right angled triangular reflecting prism of average refractive index mu . When incident rays on face AB are parallel to face BC , then they emerges from Face AC . which are also parallel to Face BC as shown in figure-l. The prism capable to do so , known as Dove Prism. In figure-ll, the Dove Prism is used for dispersion of incident light containing red colour and violet colour only. The red colour and violet colour lights are separated( displaced ) on screen by a distance Af. In reality , each ray of any colour has some width, which can be designated as d. It is clear that an observer can distinguish the red and violet rays that emerges from prism only if Delta/varphige d .Otherwise the bundles of rays will overlap and mix. Q Find the maximum value of width d of bundle of rays that can be resolved at the outlet of Dove Prism as shown in the figure-ll. |
|
Answer» `2.25xx10^(-3)`m `/_EMD + /_ MDE = /_ BEM` `beta + (90^@ - alpha) = 45^@ implies alpha = beta+ 45^@` `implies sin(beta + 45^@)> (1/mu)` `sin beta + cos beta gtsqrt(2)/mu`…..(1) According to law of refraction at POINT M, we can write `1xxsin45^@= musn beta implies sin beta = 1/(musqrt(2)) implies cos beta= sqrt(1 - 1/(2mu^(2)))` Putting these value in equation (1), we have `1/(musqrt(2)) + sqrt(1 - 1/(2mu^(2))) > sqrt(2)/mu implies sqrt(2mu^(2) -1) > implies mu gt 1` In figure-II : Replace the Dove Prism by glass CUBE of side as AB. `Delta L =(DeltaL)/sqrt(2)` ....(2) From geometry, we can write `sin beta = 1/ (mu_(r)sqrt(2))` and `sin(beta - Deltabeta)= 1/((mu_(R) + Deltamu_(R))sqrt(2))` `Delta L = atan beta - a tan (beta- Deltabeta) = a/sqrt(2mu_(g)^(2)-1) - a/sqrt(2(mu_(R) + Deltamu)^(2) -1)` `DeltaL = a/sqrt(2mu_(R)^(2) -1 )(1- sqrt((2mu_(R)^(2)-1)/(2mu_(g)^(2) + 4mu_(R)Deltamu + 2(Deltamu)^(2) -1)))` Neglecting the value `(Deltamu)^(2)`, we have, `implies DeltaL = a/(sqrt(2mu_(R)^(2)-1)) (1 -sqrt(1/(1+ (4mu_(R)Deltamu)/(2mu_(R)^(2)-1)))) = a/sqrt(2mu_(R)^(2) -1) ( 1-{1 + (4mu_(R)Deltamu)/(2mu_(R)^(2)-1)}^(1/2))` Expand binomically, we hav `+> Delta L = (2amu_(R)Deltamu)/((2mu_(R)^(2)-1)^(3/2))` Putting this value in equation (2), we have `Deltal = (sqrt(2)amu_(R)Deltamu)/((2mu_(R)^(2)-1)^(3/2))` Second method `DeltaL = (d/(dbeta)(atanbeta))xxDeltabeta` `DeltaL=(asec^(2)beta)xxDeltabeta` Also `sin beta= 1/(sqrt(2)mu_(R))` `implies cos betaDeltabeta= 1/(sqrt(2)mu_(R)^(2)) Deltamu` `implies Delta L = (asec^(2)betaxxDeltamu)/(sqrt(mu_(R)^(2)cosbeta)` `DeltaL = (2amu_(R)Deltamu)/((2mu_(R)^(2)-1)^(3/2))` 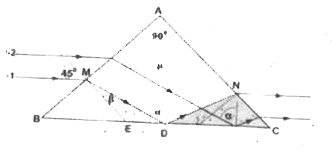
|
|
| 983. |
Define 'Q' factor and sharpness of resonant curve. |
|
Answer» Solution :Q' factor is DEFINED as the ratio of `X_(L)` or `X_(C)` to the DC, resistance, `Q=(X_(L)orX_(C))/(R)`. Sharpness of of resonant curve = `(f_(0))/(B.W)` where, `f_(0)` - resonant FREQUENCY, B.W - band WIDTH. |
|
| 984. |
(a) A mobile phone lies along the principal axis of a concave mirror. Show, with the help of a suitable diagram, the formation of its image. Explain whymagnification is not uniform ? (b)Suppose the lower half of the concave mirror's reflecting surface is covered with an opaque material. What effect this will have on the image of the object ? Explain. |
Answer» SOLUTION :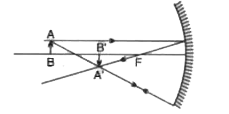 (B) Only INTENSITY WIL REDUCE. |
|
| 985. |
Obtain the maximum kinetic energy of b-particles, and the radiation frequencies of g decays in the decay scheme shown in Fig. You are given that m(""_(8)^(19)Au) = 197.968233 u m(""_(8)^(19)Hg) =197.966760 u. |
|
Answer» SOLUTION :`K_("max")(beta_(1)^(-))=0.284MeV, K_("max")(beta_(2)^(-))=0.960MeV` `V(gamma_(1))=2.627xx10^(20)Hz, v(gamma_(2))=0.995xx10^(20)Hz, v(gamma_(3))=1.632xx10^(20)Hz` |
|
| 986. |
ABC is an isosceles right angled triangular reflecting prism of average refractive index mu . When incident rays on face AB are parallel to face BC , then they emerges from Face AC . which are also parallel to Face BC as shown in figure-l. The prism capable to do so , known as Dove Prism. In figure-ll, the Dove Prism is used for dispersion of incident light containing red colour and violet colour only. The red colour and violet colour lights are separated( displaced ) on screen by a distance Af. In reality , each ray of any colour has some width, which can be designated as d. It is clear that an observer can distinguish the red and violet rays that emerges from prism only if Delta/varphige d .Otherwise the bundles of rays will overlap and mix. Q . Choose the INCORRECT option. |
|
Answer» As per figure-l, the average refractive index of Dove Prism may be greater than 1. `/_EMD + /_ MDE = /_ BEM` `beta + (90^@ - alpha) = 45^@ implies alpha = beta+ 45^@` `implies sin(beta + 45^@)> (1/mu)` `sin beta + cos beta gtsqrt(2)/mu`…..(1) According to law of refraction at point M, we can WRITE `1xxsin45^@= musn beta implies sin beta = 1/(musqrt(2)) implies cos beta= sqrt(1 - 1/(2mu^(2)))` Putting these value in equation (1), we have `1/(musqrt(2)) + sqrt(1 - 1/(2mu^(2))) > sqrt(2)/mu implies sqrt(2mu^(2) -1) > implies mu gt 1` In figure-II : REPLACE the Dove Prism by glass cube of side as AB. `Delta l =(DeltaL)/sqrt(2)` ....(2) From geometry, we can write `sin beta = 1/ (mu_(r)sqrt(2))` and `sin(beta - Deltabeta)= 1/((mu_(R) + Deltamu_(R))sqrt(2))` `Delta L = atan beta - a tan (beta- Deltabeta) = a/sqrt(2mu_(g)^(2)-1) - a/sqrt(2(mu_(R) + Deltamu)^(2) -1)` `DeltaL = a/sqrt(2mu_(R)^(2) -1 )(1- sqrt((2mu_(R)^(2)-1)/(2mu_(g)^(2) + 4mu_(R)Deltamu + 2(Deltamu)^(2) -1)))` Neglecting the value `(Deltamu)^(2)`, we have, `implies DeltaL = a/(sqrt(2mu_(R)^(2)-1)) (1 -sqrt(1/(1+ (4mu_(R)Deltamu)/(2mu_(R)^(2)-1)))) = a/sqrt(2mu_(R)^(2) -1) ( 1-{1 + (4mu_(R)Deltamu)/(2mu_(R)^(2)-1)}^(1/2))` Expand binomically, we have `implies Delta L = (2amu_(R)Deltamu)/((2mu_(R)^(2)-1)^(3/2))` Putting this value in equation (2), we have `Deltal = (sqrt(2)amu_(R)Deltamu)/((2mu_(R)^(2)-1)^(3/2))` Second method `DeltaL = (d/(dbeta)(atanbeta))xxDeltabeta` `DeltaL=(asec^(2)beta)xxDeltabeta` Also `sin beta= 1/(sqrt(2)mu_(R))` `implies cos betaDeltabeta= 1/(sqrt(2)mu_(R)^(2)) Deltamu` `implies Delta L = (asec^(2)betaxxDeltamu)/(sqrt(mu_(R)^(2)cosbeta)` `DeltaL = (2amu_(R)Deltamu)/((2mu_(R)^(2)-1)^(3/2))` 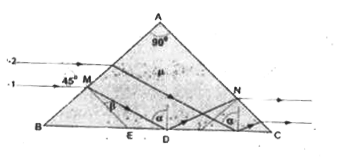
|
|
| 987. |
The maximum voltage that can be applied to 5K Omega and 8W resistor without exceeding its heat dissipating capacity is |
|
Answer» 100 V |
|
| 988. |
Find V_(ab) in an electric field vec(E)=(2hat(i)+3hat(j)+4hat(K))N//C where vec(i)_(a)=(hat(i)-2hat(j)+hat(k))mandvec(r_(b))=(2hat(i)+hat(j)-2hat(k))m |
| Answer» Answer :B | |
| 989. |
A cylindrical metallic wire is stretched to increase its length by 5%. Calculate the percentage change in its resistance. |
|
Answer» Solution :It is given that l. =l + 5% of `l = l (1 + 5/100)` As on stretching the wire its volume remains constant, HENCE A.l= A.l. `rArr A. = (Al)/(l.) = (Al)/(l (1 + 5/100) ) = (A)/( (1+ 5/100))` ` therefore ` New resistance `R. (rho l.)/(A.) = (rho l (1 + 5/100)^2)/(A ) = R.(1 + 5/100)^2 = R (1 + 10/100)` ` therefore ` PERCENTAGE increase in resistance `Delta R = (R. - R)/(R ) XX 100% = (R (1 + 10/100)-R)/(R ) xx 100%= 10%` |
|
| 990. |
Two bodies are projected at angles 30° and 60° to the horizontal from the ground such that the maximum heights reached by them are equal. Then Mark the correct answer as |
|
Answer» If a, B, C and d are correct |
|
| 991. |
Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is |
|
Answer» `(1)/(3)SQRT((Gm)/(R ))` Attractive force`=-G(mm)/(4R^(2))`. But the two masses are going round the centre of mass or the reduced mass `mu=(mm)/(m+m)` is going round a circle of radius= distance of separation `:.` Centrifugal force `=(m)/(2)omega^(2).2 R=(m)/(2)v^(2).(1)/(2R )` `rArr (m)/(2)xx(v^(2))/(2R)=(Gm^(2))/(4R^(2)) rArr v=sqrt((Gm)/(R ))` |
|
| 992. |
A copper wire of cross-sectional area 3.4 mm and length of the wire 400m, specific resistivity of copper is 1.7xx10^(-8)Omega-m Then the resistance of the wire is |
|
Answer» `20OMEGA` |
|
| 993. |
Assertion (A) : A cyclotron is a device which is sued to accelerate positively charged ions. Reason (R) : Cyclotron frequency depends on the velocity of positive ion. |
|
Answer» If both assertion and reason are true and the reason is the CORRECT explanation of the assertion. |
|
| 994. |
The degree of polarity of a convalent compound is measured by the dipole moment (mu_(bond)) of the bond defined as: mu_(bond) =Charge on one of the poles xxbond length mu_(bond) is a vector quantity. The dipole moment of a molecule is the vector addition of all the bond dipole moments present in it. For a triatomic molecule, containing two bond's like H_(2)O, mu_("molecule") is dipole mements present in it. For a triatomic molecule, containing two bond's like H_(2)O, mu_("molecule") is given by mu_("molcular")^(2) = mu_(bond)^(2) + mu_(bond)^(2) + 2mu_(bond).mu_(bond)costheta theta = bond angle The % ionic character of a bond is calculated using the equations % ionic character = (mu_(obs))/(mu_(ionic)) xx 100 mu_(ionic) = dipole moment when the molecule is assumed to be completely ionic. Which of the following compound has non zero dipole moment - |
|
Answer» `PCl_(3)` |
|
| 995. |
Find the minimum thickness of a film of refractive index 1.25, which will storngly reffect the light of wavelenght 589 nm. Also find the minimum thikness of the film to be anti - reflecting. |
|
Answer» Solution :`lambda = 589 nm = 589 xx 10^(-9) m` For the film to have strong reflection, the reflected waves should INTERFERE constructively The least optical path difference introduced by the film should be `lambda//2` . The optical path difference between the waves reflected from the two surface of the film is 2pd. Thus, for strong reflection, 2ND = `lambda//2(N - 1)` Rewriting, ` d = (lambda)/(4mu)` Substituting, `d=(589xx10^(9))/(4xx1.25)=117.8xx10^(-9)` `d = 117.8 xx 10^(-9) = 117.8 nm` For the film to be anti - reflecting, the reflected rays should interfere destructively. The least optica path difference introduced by the film should be `lambda`. The optical path difference between the waves reflected from the surface of the film is 2pd. For strong reflection. `2mud = lambda (n = 1)`. Rewriting, `d = (lambda)/(2pi)` Substituting , `d=(589xx10^(9))/(2xx1.25)=235.6xx10^(-9)` `d = 235.6 xx 10^(-9) = 235.6 nm` |
|
| 996. |
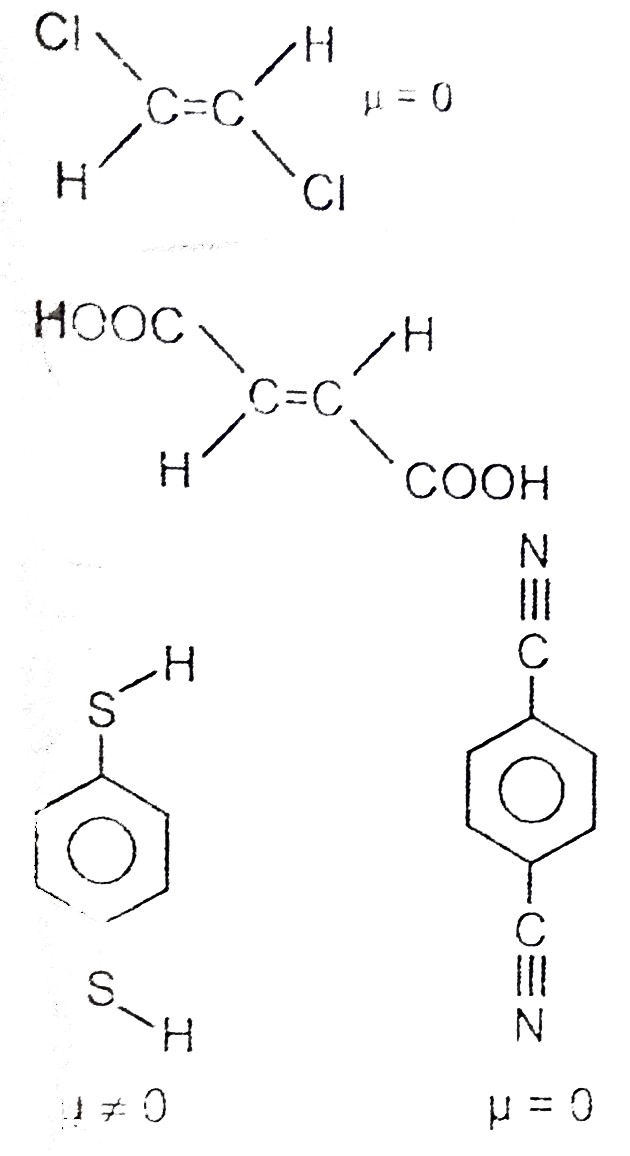
The degree of polarity of a convalent compound is measured by the dipole moment (mu_(bond)) of the bond defined as: mu_(bond) =Charge on one of the poles x bond length mu_(bond) is a vector quantity. The dipole moment of a molecule is the vector addition of all the bond dipole moments present in it. For a triatomic molecule, containing two bond's like H_(2)O, mu_("molecule") is dipole mements present in it. For a triatomic molecule, containing two bond's like H_(2)O, mu_("molecule") is given by mu_("molcular")^(2) = mu_(bond)^(2) + mu_(bond)^(2) + 2mu_(bond).mu_(bond)costheta theta = bond angle The % ionic character of a bond is calculated using the equations % ionic character = (mu_(obs))/(mu_(ionic)) xx 100 mu_(ionic) = dipole moment when the molecule is assumed to be completely ionic. Which of the follwing is //are nonpolar (mu = 0)? |
|
Answer»
|
|
| 997. |
L, C and R represent physical quantities inductance, capacitance and resistance respectively. What is the combination representing dimension of frequency? |
|
Answer» LC `=["second"^2]` `=M^0L^0T^2` (B)`(LC)^(-1/2)` As explainedin (A) `[(LC)^(-1/2)]=[M^0L^0T^2]^(-1/2)` `=M^0L^0T^(-1)` Which is DIMENSION of frequency . (C) `(L/C)^(-1/2)` Unit of `(L/C)^(-1/2)=["Ohm x Second"/("Second"/"Ohm")]^(-1/2)=[(Ohm)^2]^(-1/2)` `=[Ohm^(-1)]` `=M^(-1) L^(-2) T^3 A^2` (D) Unit of `C/L = ("second"/"ohm")/"ohm x second"="second"^2/"ohm"^2` `=[("second"/"ohm")^2]` `=(M^0L^0T^2)/(M^2L^4T^(-6)A^(-4))` `=M^(-2) L^(-4) T^4 A^4` |
|
| 998. |
Mention the differences between interference and diffraction. |
Answer» SOLUTION :
|
|
| 999. |
A network of resistance is constructed with R_(1)&R_(2) as shown in the figure . The potential at the points 1,2,3 ,,,,, N and V_(1),V_(2),V_(3) ,,,,,,, V_(n) respectively each having a potential k time smaller than previous one. Findcurrent that passes through the resistance R_(2) nearest to the V_(0) in terms V_(0) , k & R_(3). |
| Answer» Solution :`(((K-1)//k^(2))V_(0))/(R_(3))` | |
| 1000. |
Magnetic field due to 0.1 A current flowing through a circular coil of radius 0.1 m and 1000 turns at the centre of the coil is |
|
Answer» `2xx 10^(-1) T` |
|