Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1001. |
A wire in the form of a circular loop of one turn carrying a curretn I produces a magnetic field B at its centre. If the same wire is looped into a coil of 2 turns and carries the same current, then magnetic field produced at the cetre of coil is |
| Answer» ANSWER :C | |
| 1002. |
In each question, there is a table having 3 columns and 4 rows. Based on the table, there are 3 questions. Each question has 4 options (a), (b), ( c ) and (d), ONLY ONE of these four options in correct. In which condition is the total momentum after collision 10 kg m/s ? |
| Answer» Answer :B | |
| 1003. |
In each question, there is a table having 3 columns and 4 rows. Based on the table, there are 3 questions. Each question has 4 options (a), (b), ( c ) and (d), ONLY ONE of these four options in correct. In which condition is the velocity of one of the objects after collision 1.165 m/s ? |
|
Answer» (II) (ii) (J) |
|
| 1004. |
The Q-value of a nuclear reaction A + b to C + d is defined by Q=[m_(A) + m_(b)-m_(C)-m_(d)]c^(2) where the masses refer to the respective nuclei. Determine from the given data the Q-value of following reactions and state whether the reactions are exothermic or endothermic. (i) " "_(1)^(1)H+" "_(1)^(3)H (to) " "_(1)^(2)H+ " "_(1)^(2)H (ii) " "_(6)^(12)C+" "_(6)^(12)C (to) " "_(10)^(20)Ne + " "_(2)^(4)He Atomic masses are given to be m(" "_(1)^(2)H) = 2.014102 u, m(" "_(1)^(3)H) = 3.016049 u, m(" "_(6)^(12)C) = 12.000000 u, m(" "_(10)^(20)Ne) = 19.992439 u. |
|
Answer» Solution :`" "_(1)^(1)H+" "_(1)^(3)H to " "_(1)^(2)H+" "_(1)^(2)H` In terms of atomic masses `Q =[{1.007825 + 3.016049}-{2.014102 + 2.014102}] xx 931.5 MeV =- 0.00433 xx 931.5 MeV = -4.03 MeV` It is an endothermic REACTION. (ii) `" "_(6)^(12)C+" "_(6)^(12)C to " "_(10)^(20)Ne + " "_(2)^(4)He` `Q =[{12.0000 + 12.0000} - {19.992439 + 4.002603}] xx 931.5 MeV= 0.004958 xx 931.5 MeV = 4.62 MeV` The reaction is exothermic. |
|
| 1005. |
The angle of dip at a location in southern India is about 18^@. Would you expect a greater or smaller dip angle in Britain ? |
| Answer» Solution :Greater in Britain (it is about `70^@`), because Britain is closer to the magnetic NORTH POLE and DIP angle increases as ONE goes from EQUATOR towards the magnetic poles. | |
| 1006. |
Give the qualitative explanation of the action of an LC oscillator in the absence of any external ac voltage source. Assume that the capacitor is charged initially. |
|
Answer» SOLUTION :(i) At t = 0, the capacitor has energy of `(1)/(2)(q_(m)^(2))/(C)`. Energy associated with the inductor is zero. When the switch is closed, capacitor discharge, magnetic energy gets stored in the inductor. When the current reaches its maximum value `i_(m)("at "t=(T)/(4))` all the electrostatic energy is converted into magnetic energy in the inductor. Magnetic energy `-(1)/(2)Li_(m)^(2)`. Energy in the capacitor becomes zero. (ii) During the time interval from `t=(T)/(4)` to `t=(T)/(2)`, the current starts charging the capacitor until it gets fully charged `("at "t=(T)/(2))`. The polarity of the capacitor will be OPPOSITE. Energy in the inductor become zero. (iii) During the time interval from `t=(T)/(2)` to `t=(3)/(4)T`, the inductor gets the current from the capacitor, until the inductor gets the maximum current and maximum energy `((1)/(2)Li_(m)^(2))` is stored in the inductor. (iv) During the time interval from `t=(3)/(4)T` to `t=T`, the initial polarity of capacitor gets RESTORED and charging the capacitor to acquire energy of `(1)/(2)(q_(m)^(2))/(C)` This process of conversion of electrostatic energy to magnetic energy takes place without any EXTERNAL source voltage as long as the oscillating system does not lose energy in the form of heat or electromagnetic energy. (i) at t = 0  (ii) at `t=(T)/(4)`  `(T)/(4)lt t lt (T)/(2)`  (iv) at `t=(T)/(2)` 
|
|
| 1007. |
A and B are two points in a closed circuit. The potential difference across the condenser of capacity 5muFis |
|
Answer» 6V |
|
| 1008. |
Figureshows planar loops of different shapes moving out of or into a region of a magnetic field which is directed normal to the plane of the loop away from the reader. Determine the direction of induced current in each loop using Lenz’s law. |
|
Answer» SOLUTION :(i) The magnetic flux through the rectangular loop abcd increases, due to the motion of the loop into the region of magnetic field, The induced CURRENT must flow along the path bcdab so that it opposes the increasing flux. (ii) Due to the OUTWARD motion, magnetic flux through the triangular loop abc decreases due to which the induced current flows along bacb, so as to oppose the change in flux. (iii) As the magnetic flux decreases due to motion of the IRREGULAR shaped loop abcd out of the region of magnetic field, the induced current flows along cdabc, so as to oppose change in flux. Note that there are no induced current as long as the loops are completely INSIDE or outside the region of the magnetic field. |
|
| 1009. |
Three long straight and parallel wires, carrying currents are arranged as shown figure. The force experienced by the conductor 'B' of length 25 cm is |
|
Answer» `4 xx 10^(-4) N` from LEFT to RIGHT |
|
| 1010. |
A copper rod AB of length l is rotated about one endA with a constant angular velocity omega. Calculate the electric field at a distance x from the axis of rotation. Also determine PD between A and B. |
|
Answer» |
|
| 1011. |
Which colour will give maximum resolving power for a telescope ? |
|
Answer» Red |
|
| 1012. |
Explain the concept of nuclear energy with reference to binding energy curve. |
|
Answer» Solution :Nuclear energy is the energy released during a nuclear reaction. The curve of average binding energy per nucleon `(barB)` against mass number, Fig. show a long flat region form about `A =30` to `A=170`. In this region, `barB` is almost constant. However, for nuclei with Alt30 and Agt170, value of `barB` is less than the plateau value. Clearly, nuclei with mass number in the range `30leAle170` are more tightly bound than the nuclei with `Alt30` and nuclei with `Agt170`. Hence when we transmute less tightly bound nuclei reactions, the nuclear energy may be released. The nuclear reaction can thus prove to be a source of energy. Nuclear energy is released on account of mass defect in the reaction. The nuclear reactions which can be practical sources of energy are broadly of two TYPES. (1) Nuclear fission, in which a heavier nucleus breaks into lighter ones. (2). Nuclear fusion, in which lighter nuclei fuse into a heavier one. In both the case, energy released in estimated form mass defect `(DELTA m)` form EINSTIEN's mass energy relation `E=(Delta m)c^2`. |
|
| 1013. |
A straight wire is first bent into a circle of radius 'r' and then into a square of side 'x' each of oneturn. If currents flowing through them are in the ratio 4 : 5, the ratio of their effective magnetic moments is |
|
Answer» `pi/8` |
|
| 1014. |
Mention the pair of space and time varying E and B fields which would generate a plane em wave travelling in Z-direction. |
| Answer» SOLUTION :`E_x and b_y` | |
| 1015. |
A solenoidal coil has 50 turns per centimetre along its length and a cross-sectional area of 4xx10^(-4)m^(2). 200 turns of another wire is wound round the first solenoid co-axially. The two coils are electrically insulated from each other. Calculate the mutual inductance between the two coils. |
|
Answer» Solution :`n_(1) = 50` turns per cm = 5000 turns per METRE `n_(2)l=200, A=4xx10^(-4)m^(2)` `M=mu_(0)n_(1)(n_(2)l)A` `=4 pi xx 10^(-7) xx 5000 xx 200 xx 4 xx 10^(-4) H` `=5.03 xx 10^(-4)H` |
|
| 1016. |
White natural light falls on a system of two crossed Nicol prisms having between them a quartz plate 1.50 mm thick, cut parallel to the optical axis. The axis of the plate froms an angle of 45^(@ with the principle directions of the Nicol prism. The light transmitted through that system was split into the spectrum. How many dark fringes will be observed in the wavelength interval from 0.55 to 0.66mu m? The difference of refractve indices for ordinary and extraordianry rays in that wavelength interval is assumed to be equal to 0.0090. |
|
Answer» Solution :As in the previous two problems the QUARTZ plate will introduces a phase difference `DELTA`. The LIGHT on passing through the plate will remain plane polarized only for `delta = 2kpi` or `(2k + 1)pi`. In the latter case the plane of polarization of the light incident on the plate will be rotated by `90^(@)` by its so light passing through the analyser (which was originally crossed) will be a MAXIMUM. Thus dark bands will be observed only for those `lambda` for which `delta = 2k pi` Now `delta = (2pi)/(lambda) (n_(e) - n_(0))d = (2pi)/(lambda) xx 009 xx 1.5 xx 10^(-3)m` `= (27pi)/(lambda)(lambda` in `mu m`) For `lambda = 0.55` we get `delta = 49.09 pi` Choosing `delta = 48pi, 46pi, 44pi, 42pi` we get `lambda = 0.5625mu m, lambda = 0.5870 mu m, lambda = 0.6136mu m` and `lambda = 0.6429mu m`. These are the only values between `0.55 mu m` and `0.66 mu m`. Thus there are four bands. |
|
| 1017. |
A coil of inductance 0.50 H and resistance 100 Omega is connected to a 240 V, 50 Hz ac supply. What is the maximum current in the coil ? |
|
Answer» SOLUTION :`I_(m) = ( V_(m))/( |Z|)` `= ( SQRT(2) V_(rms))/( sqrt( R^(2) + X_(L)^(2)))` `:. I_(m) = ( sqrt(2)V_(rms))/(sqrt( R^(2) + 4pi^(2) f^(2) L^(2)))``( :. X_(L) = omega L = 2pi f L ) `...(1) `= ( ( 1.414 ) ( 240) )/( sqrt(( 100)^(2) + ( 4) ( 3.14)^(2) ( 50)^(2) ( 0.5)^(2)))` =1.82A |
|
| 1018. |
A coil of inductance 0.50 H and resistance 100 Omega is connected to a 240 V, 50 Hz ac supply. What is the time lag between the voltage maximum and the current maximum ? |
|
Answer» Solution :We have `tan PHI = ( X_(L ) - X_(C ))/( R )` `:. tan phi= ( 2pi f L )/( R ) ( :.` Here, `X_(C ) = 0` )...(2) `= ( 2 xx 3.14 xx 50 xx 0.5 ) /( 100)` `:. tan phi= 1.57` F= 50 Hz `T = (1)/( 50) = 0.02 sec` PHASE difference( rad )Time ` 2pi `0.02 `1.57 xx (pi )/( 180)`(t ) ` t = ( 0.02 xx 1.57 ) /( 2pi )xx ( pi )/( 180)` `= 3.2 xx 10^(-3) = 3.2 ms ` |
|
| 1019. |
Radiated energy per second gain by an electric bulb is 25 Joule/second and velocity of electromagnetic wave is c then force gain by the surface per second is …. |
|
Answer» `8.33xx10^(-8)J` |
|
| 1020. |
A particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is |
| Answer» Answer :C | |
| 1021. |
In casette tapes, the sound is recorded in the from of |
|
Answer» VARIABLE RESISTANCE on the tape |
|
| 1022. |
The equation of trajectory of a projectile thrown from a level groundnear the surface of earth is given by y = ax - bx^(2) , with y axis in vertical direction and x-axis in horizontal direction .a and b are constants. Then |
|
Answer» The range of the PROJECTILE is ` a/b` |
|
| 1023. |
What is the relation between potential difference and capacitance for same amount of charge stored ? |
| Answer» SOLUTION :`V PROP 1/C` | |
| 1024. |
A cyclotron.s oscillator frequency is 10 MHz and the operating magnetic field is 0.66 T. If the radius of its dees is 60 cm, then the kinetic energy of the proton beam produced by the accelerator is |
|
Answer» 9 MeV `k=(q^(2)B^(2)R^(2))/(2m)` Cyclotron frequency is `V=(qB)/(2pim)` or `q^(2)B^(2)=4pi^(2)m^(2)v^(2)` `k=1/(2m)(4pi^(2)m^(2)v^(2))R^(2)` `k=2pi^(2)mv^(2)R^(2)` …joule `k=(2pi^(2)mv^(2)R^(2))/e...eV` = `(2xx10xx(1.67xx10^(-27))XX(10xx10^(6))^(2)xx(0.6)^(2))/(1.6xx10^(-19))eV=7.2xx10^(6)eV=7.2MeV` |
|
| 1025. |
(A):A negative acceleration of a body is associated with a slowing down of a body. (R ):Acceleration is vector quantity. |
|
Answer» |
|
| 1026. |
Focal lengths of two lenses are f and f and dispersive powers of their materials are omega and omega^(')'. To form achromatic combination from these, which relation is correct? |
|
Answer» `omega=omega_(0), 2omega_(0), F^(')=2f` |
|
| 1027. |
In the front of the upper slit of YDSE apparatus, a thin film of a liquid of refractive index 1.40 is placed. It is a hot day and the liquid starts evaporating from the surface. A beam of light at wavelength 560 nm is incident onto the YDSE apparatus and the intensity I at the centre of the screen is monitored. Figure gives intensity I as a function of time t. The intensitychanges because of evaporation from the two sides of the film. Assume that the film is flat and has parallel sides. Also assume that the film's thickness decreases at a constant rate What can be the initial thickness of the film? |
|
Answer» `7 mum` `t=(n+1/2)XX(560xx10^(-9))/(0.4)=(n+1/2)xx1.4xx10^(-6)` SINCE we observe 3 max `ngt3` `Rightarrow (2n+1)xx0.7` mum |
|
| 1028. |
In the front of the upper slit of YDSE apparatus, a thin film of a liquid of refractive index 1.40 is placed. It is a hot day and the liquid starts evaporating from the surface. A beam of light at wavelength 560 nm is incident onto the YDSE apparatus and the intensity I at the centre of the screen is monitored. Figure gives intensity I as a function of time t. The intensitychanges because of evaporation from the two sides of the film. Assume that the film is flat and has parallel sides. Also assume that the film's thickness decreases at a constant rate If the maximum intensity is I_(0) then |
|
Answer» Intensity at `t=0 sec is I_(0)/sqrt(2)` `Rightarrow "in" t=10sec,Deltaphi=pi/15xx10=(2pi)/3` `Rightarrow phi=p+(2pi)/(3)` `I=I_(0)(cos(pi/2+pi/3))^(2)=I_(0)"sin"^(2)pi/3=3/4I_(0)` `i n t=5sec,Deltaphi=pi/15xx5=pi/3` `phi=pi+pi/3` `I=10(cos(pi/2+pi/6))^(2)=I_(0)"sin"^(2)pi/6=I_(0)/4` |
|
| 1029. |
In the front of the upper slit of YDSE apparatus, a thin film of a liquid of refractive index 1.40 is placed. It is a hot day and the liquid starts evaporating from the surface. A beam of light at wavelength 560 nm is incident onto the YDSE apparatus and the intensity I at the centre of the screen is monitored. Figure gives intensity I as a function of time t. The intensitychanges because of evaporation from the two sides of the film. Assume that the film is flat and has parallel sides. Also assume that the film's thickness decreases at a constant rate The rate of change of thickness can be |
|
Answer» `140/3 nm//sec` `(Deltat)/(DeltaT)=560/0.4=140/3` nm//s |
|
| 1031. |
Under the influence of a force, an object of mass 4 kg accelerates from 3 m/s to 6 m/s in 8s. How much work was done on the object during this time? |
|
Answer» 27J `W=DeltaK=(1)/(2)m(V^(2)-v_(0)^(2))=(1)/(4)(4kg)[(6m//s)^(2)-(3m//s)^(2)]=54J`. |
|
| 1032. |
K. E. of protons, when accelerated to one volt potential |
|
Answer» `(1)/(1840)EV` |
|
| 1033. |
In each question, there is a table having 3 columns and 4 rows. Based on the table, there are 3 questions. Each question has 4 options (a), (b), ( c ) and (d), ONLY ONE of these four options in correct. In which condition is the velocity of one of the objects after collision 35 m/s ? |
|
Answer» (I) (IV) (J) |
|
| 1035. |
Obtain the equivalent capacitance of the network in figure below. For a 300V supply determine the charge and voltage across each capacitor. |
Answer» Solution :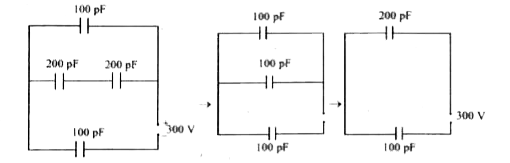 `C_("eff")=(200 xx 100 xx 10^(-12) xx 10^(-12))/(10^(-12) (300))=(200)/(3)pF` `Q=CV=(200)/(3) xx 10^(-12) xx 300 =2 xx 10^(-8)C` `V_("100pF") (C_(4))=(2 xx 10^(-8))/(100 xx 10^(-12))=200V` `V_("100pF") (C_(1))=100V` `Q=100 xx 100^(-12)=10^(-8)C` `Q_("200pF")=200 xx 10^(-12) xx 50=10^(-8)C` |
|
| 1036. |
Three resistors R_(1) = 3 k Omega,R_(2) = 2 k Omega and R_(3) = 5 k Omega have been connected to a constant current source as shown in figure. The current source supplies current I = 2 mA to the circuit. A voltmeter with R_(V) = 6 kOmega internal resistance is connected, as shown, to measure the potential difference across R_(1). (a) Find the percentage error in the measurement of potential difference (V_1) across. R_(1) caused due to finite resistance of the voltmeter. (b) If positions of R_(2) and R_(3) are interchanged will the percentage error in measurement of V_(1) increase or decrease ? |
|
Answer» |
|
| 1037. |
What is the weight of an astronaut while going up in a rocket with an acceleration 6 g if he actually weighs 75 kg, when stationary on the surface of the earth ? What is his apparent weight if the rocket falls down freely towards the earth ? |
|
Answer» Solution :When the lift is moving upwards `W_1=m(g+a)therefore600=mg+ma` When it is moving downwards `W_2=m(g-a)therefore360=mg-ma 600 +300 =mg + ma + mg - ma=2mg thereforemg=960/2= 480` REAL Weight of the MASS =480N. |
|
| 1038. |
Two charges +Q each ,are placed at the point A and B separated by a distancer r. A charge -q placed at the mid point of line AB is in a state of ____________ equilibrium.(##U_LIK_SP_PHY_XII_C01_E05_006_Q01.png" width="80%"> |
|
Answer» |
|
| 1039. |
An ac source is connected to two circuits as shown Obtain current through resistance R at resonance in both the circuits . |
|
Answer» Solution :In sericse resonance impedance is minimum `(as X_(L) = X_(C))` and equal to resistance `Z =R` `I = (V)/(Z) = (V)/( R)` `L` and `C` are in parallel `i_(1) = (V)/(X_(L)` lags voltage by `pi//2` `i_(2) = (V)/(X_(C))` leads voltage by `pi//2` `i = i_(2) -i_(1) = (V)/(X_(C) - (V)/(X_(L))` `(V)/(Z) = (V')/(X_(C)) - (1)/(X_(L))` At resonance, `X_(C) = X_(L)` `(1)/(Z) = 0 implies Z =oo` Impedance of overall circuit `Z =R + oo = oo` CURRENT through resistance `=0` 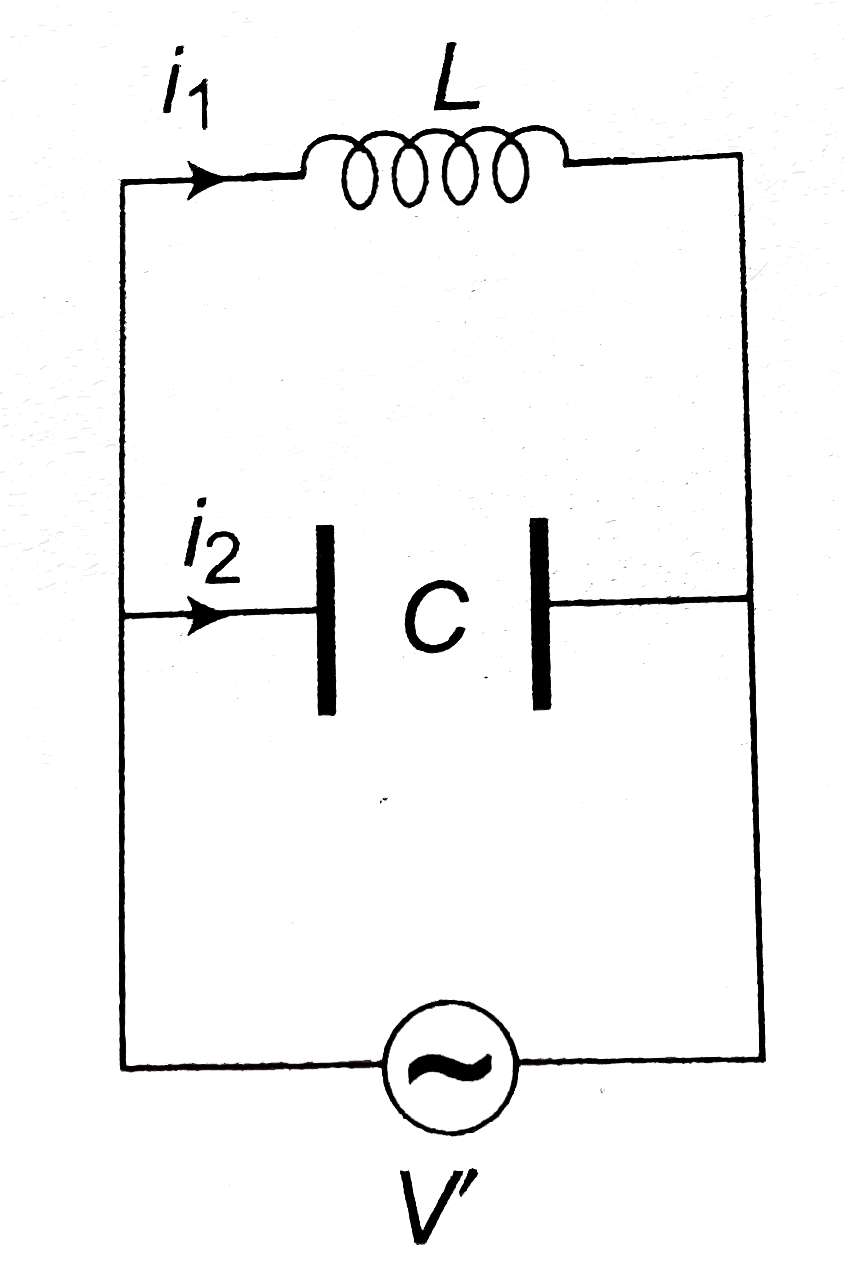  . .
|
|
| 1040. |
If we observe the single slit Fraunhofer diffraction with wavelength lambdaand slit width e , the width of the central maxima is 2 theta . On decreasing the slit width for the same lambda |
|
Answer» `theta` INCREASES |
|
| 1042. |
If a body is projected with an angle thetato the horizontal, then |
|
Answer» its velocity is always PERPENDICULAR to its acceleration |
|
| 1043. |
Two identical very small metal spheres, A and B, that are electrically neutral are fixed at a distance R On insulating handles. A third identical sphere C carrying charge Q is also connected to an insulating handle. C ia first brought into contact with A and B and then moved away from these two spheres. It is found that A and B apply F_1 force on each other. Now C with the remaining charge is again brought into contact with A and then moved away from A and B. It is found that A and B apply F_2 force on each other. Now C is further brought into contact with B and then moved away from A and B. It is found that A and B apply F_3 force on each other Finally B is moved closer to A at a distance r, such that the force between them again becomes F_1. The magnitude of F_1//F_2 is |
|
Answer» `3//4` Charge acquired by B and C touches it for the first time, `q_2=Q//4` FORCE between A and B :`F_1=1/(4piepsilon_0) ((Q/2)(Q/2))/R^2 =1/8 1/(4piepsilon_0) Q^2/R^2`…(i) Charge acquired by A when C touches if for the second time , `q_3=1/2 (Q/2+Q/4)=(3Q)/8` Force between A and B : `F_2=1/(4piepsilon_0) (("3Q"/8)(Q/4))/R^2 =3/32 1/(4piepsilon_0) Q^2/R^2`...(II) `F_1/F_2=1/8xx32/3=4/3` |
|
| 1044. |
Two identical very small metal spheres, A and B, that are electrically neutral are fixed at a distance R On insulating handles. A third identical sphere C carrying charge Q is also connected to an insulating handle. C ia first brought into contact with A and B and then moved away from these two spheres. It is found that A and B apply F_1 force on each other. Now C with the remaining charge is again brought into contact with A and then moved away from A and B. It is found that A and B apply F_2 force on each other. Now C is further brought into contact with B and then moved away from A and B. It is found that A and B apply F_3 force on each other Finally B is moved closer to A at a distance r, such that the force between them again becomes F_1. The magnitude of F_2//F_3 is |
|
Answer» `3//4` `q_4=1/2("3Q"/8+Q/4)="5Q"/16` FORCE between A and B : `F_3=1/(4piepsilon_0)(("3Q"/8)("5Q"/16))/R^2 =15/128 1/(4piepsilon_0) Q^2/R^2` …(iii) `F_2/F_3=3/32xx128/15=4/5` |
|
| 1045. |
The potential differences across the resistance, capacitance and inductance are 80 V, 40 V and 100 V respectively in an L-C-R circuit. The power factor of this circuit is |
|
Answer» 0.8 `=(100-40)/80` `=60/80=3/4` From FIGURE, power FACTOR = cos `phi` `=4/5`= 0.8 
|
|
| 1046. |
Two identical very small metal spheres, A and B, that are electrically neutral are fixed at a distance R On insulating handles. A third identical sphere C carrying charge Q is also connected to an insulating handle. C ia first brought into contact with A and B and then moved away from these two spheres. It is found that A and B apply F_1 force on each other. Now C with the remaining charge is again brought into contact with A and then moved away from A and B. It is found that A and B apply F_2 force on each other. Now C is further brought into contact with B and then moved away from A and B. It is found that A and B apply F_3 force on each other Finally B is moved closer to A at a distance r, such that the force between them again becomes F_1. The magnitude of r/R is |
|
Answer» `SQRT(15/16)` `15/128 1/(4piepsilon_0) Q^2/r^2 =1/8xx1/(4piepsilon_0) Q^2/R^2 rArr 15/(128r^2) =1/(8R^2) rArr r=R sqrt(15/16)` |
|
| 1047. |
The size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30cm is 2cm. If a concave lens of focal length 20cm is placed between the convex lens and the image at a distance of 26cm from the convex lens, calculate the new size of the image. |
|
Answer» 1.25cm `(1)/(v)-(1)/(4)=(1)/(-20)RARR v=5cm,(h_(2))/(h_(1))=|(v)/(u)|` `rArr h_(2)=2x(5)/(4)=2.5cm` 
|
|
| 1048. |
Two pointcharges q_(1) and q_(2) of magnitude + 10^(-8) c and -10^(-8) crespectively are placed 0.1 m apart calculate the electricfields at points a, b and c |
|
Answer» Solution :The electricflield vector `E_(1A)` at a due to the positive charge `q_(1)`point towards the right and has a magnitude `E_(1A)=(9xx10^(9)Nm^(2)C^(2)XX(10^(-8)C))/(0.05 m)^(2)=3.6 xx10^(4) NC^(-1)`the electirc field vectors`E_(2A)`at a due to the negative charge `q_(2)` pointsof the total electric field `E_(A)`at A is `E_(A)` is directedtowards the right the electricfieldvector `E_(1B)`at B due to thepositive charge `q_(1)` pointstowards the leftand has a manitude the magnitude of the total electricfieldat Bis `E_(B)` is directed towards the left The magnitude of each electricfieldvectorat pointc due to charge `q_(1)` and `q_(2)`is `E_( c)=E_(1c)` cos `(PI)/(3)+E_(2c)` cos `(pi)/(3)=9xx10^(3) Nc^(-1)` `E_(c )` points towards the right |
|
| 1049. |
The electric field intensity produced by the radiations coming from 100W bulb at a 3m distanceis E. The electric field intensity produced by the radiations coming from 50W bulb at the same distance is……. |
|
Answer» `E/2` `therefore I prop P` (Here R is constant) `therefore I_1/I_2=P_1/P_2 IMPLIES E_1/E_2=100/50 implies I_2=E/2` |
|
| 1050. |
A 12 Omega resistor and a 0.21 henry inductor are connected in series to an A.C. source operating at 20 volt, 50 cycle/second. What is the phase angle between the current and the source voltage ? |
|
Answer» `30^@` `TAN delta =(OMEGAL)/R=(2pif)/R=(2xx3.14xx50xx0.21)/12` `THEREFORE tan delta`= 5.495 `therefore delta=79^@ 42.` (approximate ) `therefore delta approx 80^@` |
|