Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2051. |
In a neutral conducting hollow sphere of inner and outer radii 5 cm and 10 cm respectively, a point charge Q= 1C is placed at point A, that is 3 cm from the centre C of the hollow sphere. An external uniform electric field of magnitude 20 N/C is also applied. Net electric force on this charge is 15 N, away from the centre of the sphere as shown. Then find : (a) Force due to external electric field on the outer surface of the shell (b)Net force on shell. (c) Net force on point charge due to shell. |
|
Answer» |
|
| 2052. |
LANDSAT series of satellites move in near polar orbits at an altitude of |
|
Answer» 3600 km |
|
| 2053. |
The current through an element is shown in the figure. Determine the total charge that pass through the element ata) t= 0s, b) t = 2s, c) t = 5s |
Answer» Solution : Rate of flow of charge is called current, `I=(AQ)/(DT)` Total charge PASS through ELEMENT, `dq=I, dt` (a) At t = 0 s, I = 10 A `dq=I dt=10xx0=0C` (b) At t = 2 s, I = 5 A `dq=I dt = 5xx2=10C` (c ) At t = 5s, I = 0 `dq=Idt=0xx5=0 C` |
|
| 2054. |
A convex lens is dipped in a liquid, whose refractive index is equal to the refractive index of the lens. Then, its focal length will |
|
Answer» become zero |
|
| 2055. |
Paschen series of hydrogen spectrum lies in UV region and the Lyman series lies in IR region. |
| Answer» SOLUTION :Lyman SERIES lies in UV region and Paschen series lies in IR region of SPECTRUM. | |
| 2056. |
When white light is passed through an unexcited gas,what can you observe in the spectrum of the transmitted light?why? |
| Answer» Solution :The SPECTRUM of the TRANSMITTED light CONSIST of some DARK lines CALLED the absorption lines this happens because the gas absorbs its own characteristics wavelength. | |
| 2057. |
The area of cross-section length and density of a piece of a metal of atomic weight 60 are 10^(-6)m^(2), 1m and 5xx10^(3)kg//m^(3) respectively. If every atom contributes one free electron and the drift velocity of electrons in the metal when a current of 16A passes through it is k xx 10^(-3) m//s, find the value of k. Given that Avagadro.s number N_(A)=6xx10^(23)//"mol" and charge on an electron e=1.6xx10^(-19)C. |
|
Answer» |
|
| 2058. |
P is a point on an equipotential surface S. The field at P is E. |
|
Answer» E is perpendicular to S in all cases. |
|
| 2059. |
Which of the following will not change if dielectric slab is introduced in a charged condenser ? |
|
Answer» Charge |
|
| 2060. |
(i) Define 'activity' of a radioactive material and write its S.I. unit. (ii) Plot a graph showing variation of activity of a given radioactive sample with time. (iii) The sequence of stepwise decay of a radioactive nucleus is D overset(alpha) (to) D_(1) overset(beta-) (to) D_(2) If the atomic number and mass number of D_(2) are 71 and 176 respectively, what are their corresponding values for D ? |
|
Answer» Solution :(i) The total decay rate (of a SAMPLE) at the given instant i.e. the number of radio-nuclides DISINTEGRATING per unit TIME is CALLED the activity of that sample. The SI unit for activity is becquerel (Bq). (ii) Graph: 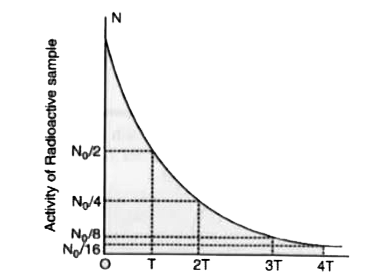 (III) `72 and 180`. |
|
| 2061. |
A coil with 1500 turns, a radius of 5.0 cm and a resistance of 12 Omega surrounds a solenoid with 240 turns // cm and a radius of 4 cm , see figure. The current in the solenoid changes at aconstant rate from 0 to 20 A in 0.10 s. Calculate the magnitude of the induced current (in mA) in the 1500 turn coil (pi^(2)=10 Neglect self inductance of the coil). |
|
Answer» `=150xx4pixx10^(-7)xx(230xx10^(2))/100xx2/0.1xxpixx(4.5xx4.5)/10^(4)` `i=varepsilon/12=(600pi^(2)xx460xx10^(3)xx10^(-7))/12xx(4.5)^(2)/10^(4)` `=0.04657500xx10^(-6)` `approx 5A` |
|
| 2062. |
The velocity of a projectile when at its greatest height is sqrt((2)/(3)) of its velocity when at half of its greatest height find the angle of projection |
|
Answer» Solution :STEP 1 : we know that, velocity of a projectile at half of MAXIMUM height `U= sqrt((1+ cos^(2) theta)/(2))` Step 2 :given that `u cos theta sqrt((2)/(5)) xx u sqrt(((1+ cos^(2) theta))/(2))` Squaring on both sides `u^(2) cos^(2) theta=(2)/(5) u^(2)((1+cos^(2) theta)/(2))` `10 cos theta=2+ 2 cos theta` `rArr 8 cos^(2) theta=2 rArr cos^(2) theta =(1)/(4) rArr theta =60^(@)` |
|
| 2063. |
In a CE amplifier , the input ac signal to be amplified is applied across |
|
Answer» FORWARD BIASED emitter-base JUNCTION 
|
|
| 2064. |
An inductor 20 mH, a capacitor 50 muF and a resistor 40 Omega are connected in series across a source of emf, V = 10 sin 340 t. the power loss in AC circuit is |
|
Answer» 0.67 W. `X_(L) = OMEGAL = 340 xx20 xx10^(-3)= 6.8Omega` . `X_(C)= (1)/(omegaC) = (1)/(340xx50xx10^(-6))= 58.8 Omega` `Z = SQRT(R^(2)+(X_(C)-X_(L))^(2))=65.6Omega` `P= (1)/(2) (V_(0)^(2))/(Z) cos delta= (1)/(2) xx(100)/(65.6)xx(40)/(65.6)` `IMPLIES P =0.46W `. Hence option (b) is correct . |
|
| 2065. |
A metal plate of mass 200g is balanced in mid air by throwing 40 balls per second, each of mass 2g vertically upwards from below. The balls get rebounded with the same speed with which they strike the plate. Find the speed with which the balls strike the plate. |
|
Answer» |
|
| 2066. |
A bar magnet of magnetic moment m and moment of inertia I (about centre, perpendicular to length) is cut into two equal pieces, perpendicular to length. Let T be the period of oscillations of the original magnet about an axis through the mid point, perpendicular to length, in a magnetic field B. What would be the similar period T' for each piece ? |
|
Answer» Solution :Time period of bar magnet in magnetic FIELD B `T= 2pi sqrt((I)/( MB) ) ""…(1)` where M = magnetic moment of magnet B = uniform magnetic field Here `I= (ml^(2) )/( 12)` where m = mass of magnet l = LENGTH of magnet I = moment of INERTIA of magnet When magnet is cut into two equal pieces, perpendicular to length then moment of inertia I. of each piece of magnet about an axis perpendicular to the length passing through its centre is, `therefore I. = (m)/(2) ((l)/(2))^(2) .(1)/(12)` `I. = (ml^(2) )/( 12 xx 8 ) = (1)/(8) ""...(2)` Original magnetic moment `M = (2l) q_(m)` DIPOLE moment of each piece `M. = ((2l)/( 2))q_m` `M. = (M)/(2)""...(3)` Period of each piece, `T. = 2pi sqrt((I.)/( M.B))` `= 2pi sqrt((I//8)/( (M//2)B) ) ""` [ From EQU. (2) and (3) ] `= 2pi sqrt((1)/(4) (1)/(MB) )` `= (1)/(2) 2pi sqrt((I)/(MB))` `T.= (T)/(2)""` [From equation (1)] |
|
| 2067. |
A sinusoidal wave of angular frequency 1200 rad/s and amplitude 3.00 mm is sent along a cord with linear density 4.00 g/m and tension 1200 N. (a) What is the average rate at which energy is transported by the wave to the opposite end of the cord? (b) If simultaneously, an identical wave travels along an adjacent identical cord, what is the total average rate at which energy is transported to the opposite ends of the two cords by the waves? IT, instead, those two Waves are sent along the same cuid simultaneously, what is the tolal average rate at which they transport energy when their phase difference is (c) 0, (d) 0.4pi rad, and (e) pi rad? |
|
Answer» |
|
| 2068. |
Suppose you are given a chance to repeat the alpha particle scattering experiment using a thin sheet of solid hydrogen in place of gold ofil (hydrogen is a solid at temperature below 14 K). What results do you expect? |
| Answer» SOLUTION :The basic purpose of scattering experiment is defeated, because solid hydrogen will be a much ligther target compared to the alpha particle acting as projectile. According to theory of ELASTIC collisions, the target hydrogen will move much FASTER compared to alpha, after the COLLISION. We cannot determine the size of hydrogen NUCLEUS. | |
| 2069. |
Assertion:An alpha-particle is emitted when uranium 238 decays into thorium Reason : The decay of uranium 238 to thorium is repesented by ._92^238 U to ._90^234Th + ._2^4 He . The helium nuclei is called an alpha particle. |
|
Answer» If both ASSERTION and reason are true and reason is the CORRECT explanation of assertion . |
|
| 2070. |
The reading of a pressure meter attached with a closed water pipe is 3.5 xx 10^(5) N//m^(2). On opening the valve, the reading of the pressure meter is reduced to 3 xx 10^(5) N//m^(2). Calculate the speed of water flowing in the pipe. |
|
Answer» 10 m/s `(P_(1))/p+1/2v_(1)^(2)=(P_(2))/p+1/2v_(2)^(2)` `(3.5xx10^(5))/(10^(3))+0=(3xx10^(5))/(10^(3))+1/2v_(2)^(2)` `350-300=1/2v_(2)^(2)` `v_(2)^(2)=50xx2=100` `v_(2)=10m//s` So the correct choice is (a). |
|
| 2071. |
Two short bar magnets A and B of dipole moments 0.15 A m^(2) and 1.2 A m^(2) respectively are placed with their axes along the same line with their centres 0.15 m apart. The dipole moments due to A and B point in opposite directions. What is the position of the point, between the two magnets, where the resultant induction is zero? |
|
Answer» 10 cm from the centre of A `:. B_(1) = B_(2)` (in magnitude) ` therefore mu_(0)/(4pi)(2m_(1))/d_(1)^(3)=mu_(0)/(4pi)(2m_(2))/((0.15-d_(1))^(3))` `IMPLIES (0.15)/d_(1)^(3)=(1.2)/((0.15-d_(1))^(3))implies1/d_(1)^(3)=8/((0.15-d_(1))^(3))` `implies 8d_(1)^(3) = (0.15 - d_(1))^(3)` Taking cube ROOTS of both sides, we get `2d_(1) = 0.15 - d_(1)or 3d_(1) = 0.15` `implies d_(1) = 0.05 m = 5cm` `therefore` P is at a distance of 5 cm from the centre of A. 
|
|
| 2072. |
An object of length 10 cm is placed at right angles to the principal axis of a mirror of radius of curvature 60cm such that its image is virtual, erect and has a length 6 cm. What kind of mirror it is and also determine the position of the object ? |
|
Answer» Concave 20 CM from the MIRROR |
|
| 2073. |
Which of the following modulated signal has the best noise - tolerance ? |
|
Answer» long - WAVE |
|
| 2074. |
If X stands for the magnelic susceptibility of a substance. mu for its magnetic permeability and to mu_(0) the perincability of free space, then |
|
Answer» for a paramagnetic substance `X gt 0, MU gt 0` `X = mu_(r) - 1` and again we KNOW that `mu_(r) = mu/mu_(0)` For paramagnetic substance, `X gt0` `therefore mu_(r) gt 1 or mu gt mu_(0)` For diamagnetic substance, `-1 le X le 0` `therefore 0 le mu_(r) lt 1 or mu lt mu_(0)` For ferromagnetic substance, `X gt gt 1` `therefore mu gtgt mu_(0)` |
|
| 2075. |
A 50V, 10 W lamp is run on 100V, 50Hz ac mains Calculate the inductance of the choke coil required. |
|
Answer» <P> Solution :Voltage marked on lamp, `V=50V`Power, P = 10W `therefore"RESISTANCE of lamp, R"=(V^(2))/(P)=(50xx50)/(10)=250Omega`. `"Current rating of lamp, "I_("rms")=(P)/(V)=(10)/(50)=(1)/(5)A` The given circuit is equivalent of LR circuit. Here `E_("rms")=100V, v=50Hz` When the lamp is worked on a.c., the impedance of the circuit is `Z_(L)=(E_("rms"))/(I_("rms"))=(100)/((1)/(5))="500 ohm"` `Z_(L)^(2)=R^(2)+Omega^(2)L^(2)(OR)Z_(L)^(2)=R^(2)+4pi^(2)v^(2)L^(2)` `therefore 4pi^(2)v^(2)L^(2)=z_(L)^(2)-R^(2) or L^(2)=(Z_(L)^(2)-R^(2))/(4pi^(2)^(2))` `L^(2)=((500)^(2)-(250)^(2))/(4XX(3.14)^(2)xx(50)^(2))=(187500)/(98596)=1.9 or L=1.38H` |
|
| 2076. |
The system of block and wedges all of same mass shown in the figure is released from rest. All surfaces are smooth. Then: |
|
Answer» The speed of block `A` when it falls `50cm` is `2sqrt(2)m//s` Velocity direction of `A,B` and `C`  `1/2mv^(2)+1/2m(V^(2)+(v^(2))/4)+1/2(MV^(2))/4=2mgh` `v=sqrt(8/5gh)=2sqrt(2)m//s` |
|
| 2077. |
A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from to 20 A in 0.5 s, what is the change of flux linkage with the other coil ? |
|
Answer» SOLUTION :Here `M =1.5 H, dl_(1), = 20 - 0 = 20 A and dt = 0.5 s` `THEREFORE` Change of magnetic FLUX linked with the other COIL `|dphi_(2)| = M dl_(1) = 1.5 xx 20 = 30 Wb`. |
|
| 2078. |
Mention the various energy losses in a transformer. |
|
Answer» Solution :i. Core loss or Iron loss This loss takes place in transformer core. Hysteresis loss (REFER SECTION 3.6) and eddy current loss are known as core loss or Iron loss. When transformer core is magnetizedd and demagnetized REPEATEDLY by the alternating voltage appliedacross primary coil, hysteresis takes place due to which some energyis lost in the form ofheat. Hysteresis loss is minimized by using steel of high silicon content in making transformer core. Alternating magnetic flux the coreinduces eddy currents in it. Therefore there is energy loss due to the flow of eddy current, called eddy current loss which is minimized by using very thin laminations of transformer core. ii. Copper loss Transformer windings have electrical resistance When an electric current flows through them, some amount of energy is dissipated due to joule heating. This energy loss is called copper loss which is minimized by using wires of larger diameter. iii. Flux LEAKAGE Flux leakage happens when the magnetic lines of primary coil not completely linked with secondary coil. Energy loss due to this flux leakage is minimized by winding coils ONE over the other. |
|
| 2079. |
A ray of light having intensity 0.5 (W)/(m^2) is incident perpendicular to the glass slab having refractive index 1.5. What will be intensity of partially refracted ray ? |
|
Answer» `0.04(W)/(m^2)` `I_r=I_0((n_2-n_1)^2)/((n_2+n_1)^2)` `=0.5((1.5-1.0)^2)/(1.5+1.0)^2` `=0.5xx(0.25)/(6.25)` `THEREFORE I_r=0.02(W)/(m^2)` |
|
| 2080. |
From the given circuit find the value of I. |
|
Answer» <P> Solution :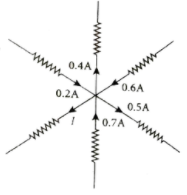 APPLYING Kirchoff.s rule to the POINT P in the circuit, The arrows pointing towards P are POSITIVE and AWAY from P are negative. Therefore, `0.2A-0.4A+0.6A-0.5A+0.7A-I=0` `1.5A-0.9A-I=0` `0.6A-I=0` `I=0.6A` |
|
| 2081. |
The power factor of a circuit containing a lamp of resistance 100 Omega, a choke coil of inductance 0.2 H and a condenser of capacitance 1 mH connected in series with an alternating emf of frequency 50 Hz is |
|
Answer» 1.86 `=62.8kOmega` `X_(C)=(1)/(2pifC)=(1)/(2xx3.14xx50xx1xx10^(-6))` `=3.185Omega` Power FACTOR `=cosphi=(R)/(Z)` `=(R)/(sqrt(R^(2)+(X_(L)-X_(C))^(2)))` `=(100)/(sqrt(100^(2)+(62.8-3.185)^(2)))` `=0.859~~0.86` |
|
| 2082. |
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundnce on earth. The three isotopes and their masses are ._(12)^(24)Mg (23.98504 u), ._(12)^(25)Mg (24.98584 u) and ._(12)^(26)Mg(25.98259 u). The natural abundance of ._(12)^(24)Mg is 78.99 % by mass. Calculate the abundances of other two isotopes. |
|
Answer» Solution :Let the ABUNDANCE of `._(12)Mg^(25)` by mass be x% therefore, abundance of `._(12)Mg^(26)` by mass = (100 - 78.99) - x% = (21.01) - x% Now AVERAGE atomic mass of magnesium is `24.312 = (23.98504xx78.99+24.98584+25.98529 (21.01 - x))/(100)` on SOLVING we get x = 9.303 % for `._(12)Mg^(25)` and for `._(12)Mg^(26), (21.01 -x) = 11.71 %` |
|
| 2083. |
The loudness of sound is related to: |
|
Answer» its frequency |
|
| 2085. |
The simplest frame of reference is coordinate system. |
|
Answer» CARTESIAN |
|
| 2086. |
How does the resolving poer of a telescope change when objective of larger aperture is used? |
|
Answer» SOLUTION :R.P. of a TELESCOPE `=FRAC{D}{1.22lambda}` when the aperture of the objective D is larger, the RESOLVING POWER of the telescope will be greater. |
|
| 2087. |
An electron is in a one-dimensional trap with zero potential energy in the interior and infinite potential energy at the walls. A graph of its wave function y(x) versus x is shown in the following figure. The value of quantum number n is |
|
Answer» |
|
| 2088. |
The minimum wavelength of x-ray emitted by x-ray tube is 0.4125A^@ The accelerating voltage is : |
|
Answer» 30 KV |
|
| 2089. |
A cylindrical container filled with a liquid is being rotated about its central axis at a constant angular velocity omega. Four points A, B, C and D are chosen in the same plane such that ABCD is a square of side length a and AB is horizontal while BC is vertical. A and D lie on the axis of rotation. Let the pressure at A, B, C and D be denoted by P_(A), P_(B), P_(C ) and P_(D). Which of these options is correct ? |
|
Answer» `P_(C )GT P_(A)` for all values of `omega , P_(B)lt P_(D)` only if `omega gt sqrt((2G)/(a))` `P_(D)=P_(A)+rhoga` `P_(C)=P_(D)+(1)/(2)rhoomega^(2)a^(2)=P_(A)+rhoga+(1)/(2)rhoomega^(2)a^(2)` Therefore, `P_(C)gtP_(A)` for all values of `omega and P_(B)gtP_(D)` only if `omegagtsqrt((2g)/(a))` |
|
| 2090. |
Plane-polarized light of wavelength 0.59mu m falls on a trihedral quartz prism P (Fig.) with refracting angle Theta = 30^(@). Inside the prism light propagates along the optical axis whose direction is shwon by hatching. Behind the Polaroid Pol an interference pattern of bright and dark fringes of width Deltax = 15.0mm is pbserved. Find the specific rotation constant of quartz and the distribution of intensity of light behind the Polaroid. |
|
Answer» Solution :Plane polarized light on entering the wedge decomposes into right and LEFT circualry polarized light which travel with difference speeds in `P` and the EMERGENT light gets its plane of polarization rotated by an angle which depends on the disatnce travelled. Given that `Delta x =` fringe width `Delta x tan theta =` difference in the path LENGTH traversed by two rays which from successive bright or dark fringes. Thus `(2pi)/(lambda) |n_(R) - n_(1)| Delta x tan theta = 2pi` Thus `alpha = (pi Delta N)/(lambda) = pi//Delta x tan theta` `= 20.8 ang deg//mm` Let `x =` distance on the polaroid Pol as MEASURED from a maximum. Then a ray that falls at this disatnce traverse an extra distance equal to `+- tan theta` and hence a rotation of `+- alphax tan theta = +- (pix)/(Deltax)` VBy malus'law the intensity at this point will be `cos^(2) ((pix)/(Deltax))`. 
|
|
| 2091. |
A charge Q is uniformly distributed over the surface of nonconducting disc of the radius R. The disc rotates about an axis perpendicular to its planes and passing through its centre with an angular velocity 0. As a result of this rotation a magnetic field of induction B is obtained at the centre of the disc if we keep both the amount of charge placed on the disk and its angular velocity to be constant and varying the radius of the disc then the variation of the magnetic induction at the centre of the disc will be represented by the figure. |
|
Answer»
|
|
| 2092. |
(a) Explain two features to distinguish between the interference patternn in Young's double-slit experiment with the diffraction pattern obtained due to a single-slit. (b) A monochromaticlight of wavelength 500 nm is incident normally on a single-slit of width 0.2mm to produce a diffraction pattern. find the angular width of the central maximum obtained on the screen. Estimate the number of fringes obtained in Young's double-slit experiment with fringe width 0.5mm, which can be accommodated within the region of total angular apread of the central maximum due to single-slit. |
|
Answer» Solution :(b) Here wavelength of MONOCHROMATIC light `lamda=500nm=500xx10^(-9)m=5xx10^(-7)` m and slit width `a=0.2mm=0.2xx10^(-3)m=2.0xx10^(-4)m` `THEREFORE` angular width of central diffraction maximum `alpha=(2lamda)/(a)=(2xx5xx10^(-7))/(2.0xx10^(-6))=5xx10^(-3)` radian Iit means that central diffraction maximum extends from `theta=0` to `theta=pm(lamda)/(a)=2.5xx10^(-3)rad`. If .D. be the DISTANCE of screen from the single-slit then it means that central diffraction maximum extends from `y=0` to `y=pmDtheta=2.5xx10^(-3)D`. As fringe width of Young.s double-slit experiment `beta=0.5=0.5xx10^(-4)m=5.0xx10^(-3)m`, hence number of interference fringes on either side of central maxima and lying within the single-slit diffraction maximum are `n=(2.5xx10^(-3)D)/(5.0xx10^(-3))=(D)/(2)`. `therefore` Total number of interference fringes which can be accommodated withhin the region of total angular SPEED of the central maximum due to single-slit `=(2n+1)=((2D)/(2)+1)=(D+1)`. |
|
| 2093. |
Two cells A and B with same e.m.f. of 2 V each and with internal resistance r_A = 3.5 Omega and r_B = 0.5 Omega are connected in series with an external resistance R = Omega RFind the terminal voltages across the two cells. |
|
Answer» Solution :We know `i= V/R =(epsi)/(R+r)` CURRENT through the circuit `i= (epsi)/((R+r)) = (2+2)/((3+3.5 + 0.5))= 4/7` i) `R= 3 Omega , r_A = 3.5 Omega , E= 2V` Terminal voltage across `A, V_A = E - ir_A ` `= 2 - 4/7 xx 3.5 = 0 `volt ii) `r_B = 0.5 Omega, R = 3 Omega , in = 2V` Terminal voltage across B, `V_B = E- ir_B` `= 2- 4/7 xx 0.5 = 1.714 ` volts |
|
| 2094. |
Explain Amplitude modulation and AM Band width. Give a few advantages of AM. |
|
Answer» Solution :Amplitude modulation. In amplitude modulation, the amplitude of the carrier wave is varied in accordance with the modulating SIGNAL, while frequency of the carrier wave remains constant. Band width It is clear from the figure that modulated signal lies in frequency range from `omega_(c)-omega_(m)` to `omega_(c)+omega_(m)i.e.,2omega_(N)` the band width of the transmitted signal. `:.` Band width `=2xx` Frequency of audio signal. If an audio signal has frequency ranging from `omega_(1)` to `omega_(2),` then each frequency in audio signal PRODUCES a pair of side bands on modulation. Entire signal produces two side bands symmctrically disposed about carrier waves as shown in figure.  Advantages of AM `1.` The channel width of AM is much less `((1)/(10)th)` the channel width required for FM. `2`. Reception of AM is not limited to line of sight like FM. `3`. The equipment required for transmission and reception of AM is more simple than for FM. |
|
| 2095. |
In a double slit experiment, instead of taking slits of equal widths one slit is made twice as wide as the other. Then in the interference pattern : |
|
Answer» the INTENSITY of both the MAXIMA and MINIMA increase. |
|
| 2096. |
If 200 MeV of energy is released in the fission of one nucleus of ._92U^235, The number of nuclei that must undergo fission to produce energy of 1000J in 1 sec is |
|
Answer» `3.125xx10^13` |
|
| 2097. |
A series circuit consisting of a capacitor with capacitance with capacitance C, a rasistance R, and a coil with inductance L and negligible activeresistance is connected to an oscillator whose frequency can be varied without changing the voltag amplitude. Find the frequency at which the voltage amplitude is maximum (a) across the capacitor , (b) across the coil. |
|
Answer» Solution :`(a) v_(c)=(1)/( omegaC) (V_(m))/( sqrt(R^(2)+(omegaL-(1)/( omegaC))^(2)))` `=( V_(m))/( sqrt( (omegaRC)^(2)+ ( omega^(2) LC-1)^(2)))=(V_(m))/( sqrt(((omega^(2))/( omega_(0)^(2))-1)^(2)+ 4 beta^(2) omega^(2) // omega_(0)^(4)))` `=(V_(m))/( sqrt(((omega^(2))/( omega_(0)^(2))-1-( 2 beta)/( omega_90)^(2))^(2)+(4 beta^(2))/( omega_(0)^(2))-( 4 beta^(4))/( omega_(0)^( 4))))` Thisis maximum when `omega^(2)=omega_(0)^(2)- 2 beta^(2) = (1)/( LC)-(R^(2))/( 2L^(2))` `(b)` `V_(L)=I_(m) omegaL=Vm(omegaL)/( sqrt(R^(2)(omegaL-(1)/( omegaL))^(2)))` `=( V_(m)L)/( sqrt((R^(2))/(omega^(2))+(L-(1)/( omega^(2)C))^(2)))=(V_(m)L)/(sqrt(L^(2)-(1)/( omega^(2))((2L)/(C)-R^(2))+(1)/( omega^(4)C^(2))))` `=(V_(m)L)/( sqrt(((1)/( omega^(2)C)-(L- ( CR^(2))/( 2)) )^(2)+L^(2)- ( L- (1)/( 2) CR^(2))^(2)))` This is maximum when `(1)/( omega^(2)C)=L-(1)/( 2) CR^(2)` or ` omega^(2) =( 1)/( LC-(1)/(2) C^(2) R^(2))=(1)/( (1)/( omega_(0)^(2))-( 2 beta^(2))/( omega_(0)^(4)))` `=( omega_(0)^(4))/( omega_(0)^(2)-2 beta^(2)) `or ` omega=( omega_(0)^(2))/( sqrt( omega_(0)^(2)-2 beta^(2)))` |
|
| 2098. |
speed of wave y = a sin (omega - 2pix/lambda) is given by |
|
Answer» |
|
| 2099. |
The equivalent capacitance between A and B in the circuit will be |
| Answer» Answer :D | |



