Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2851. |
In Polygonum type of embryo sac, the cells are ve |
|
Answer» Haploid |
|
| 2852. |
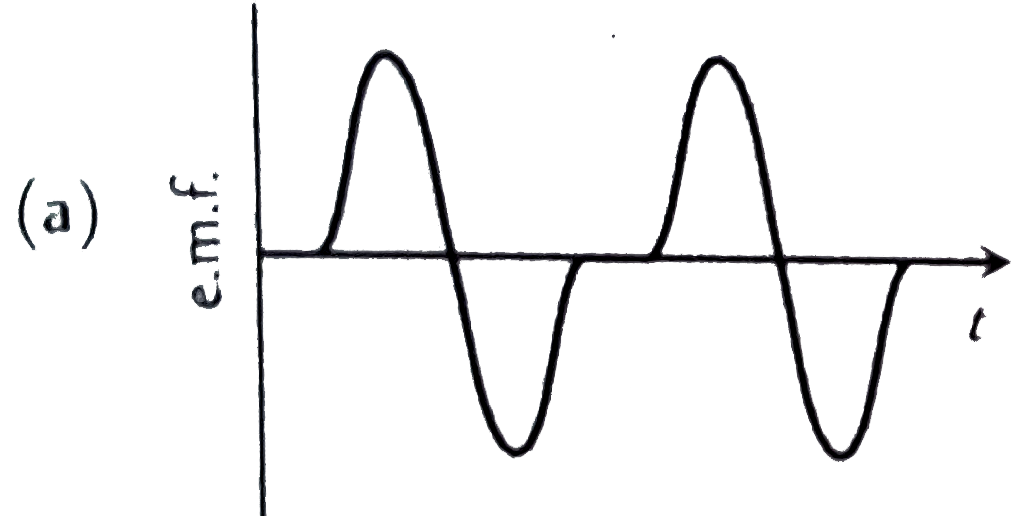
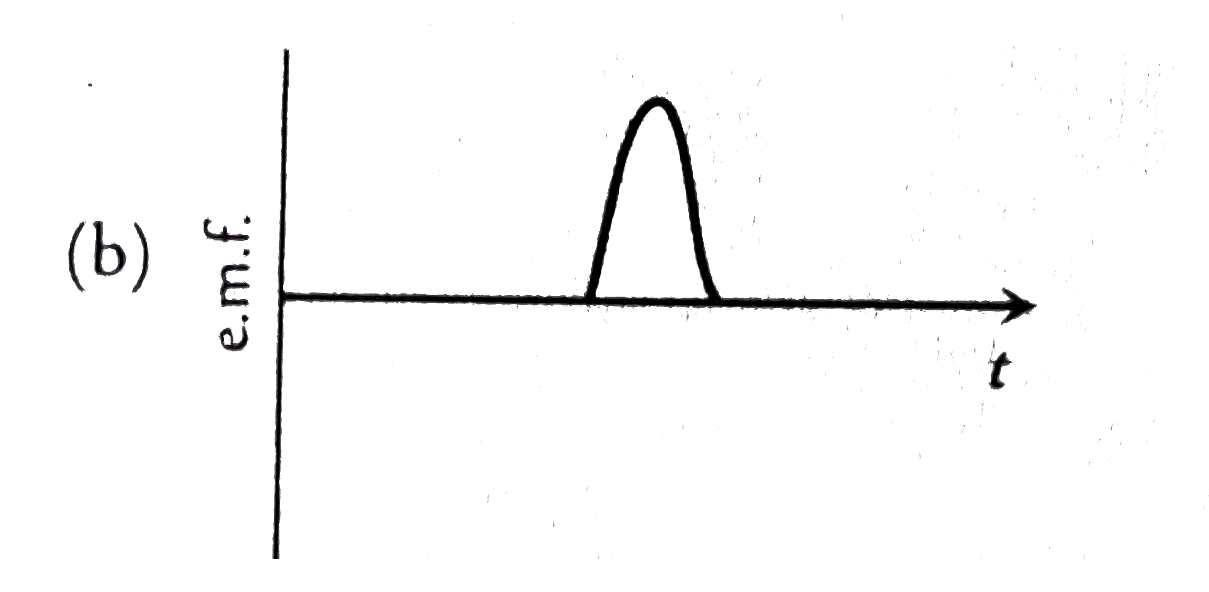
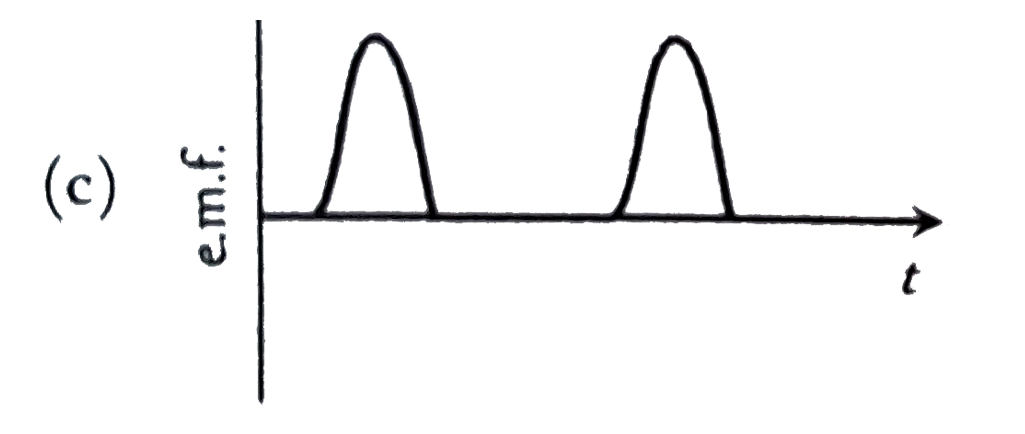
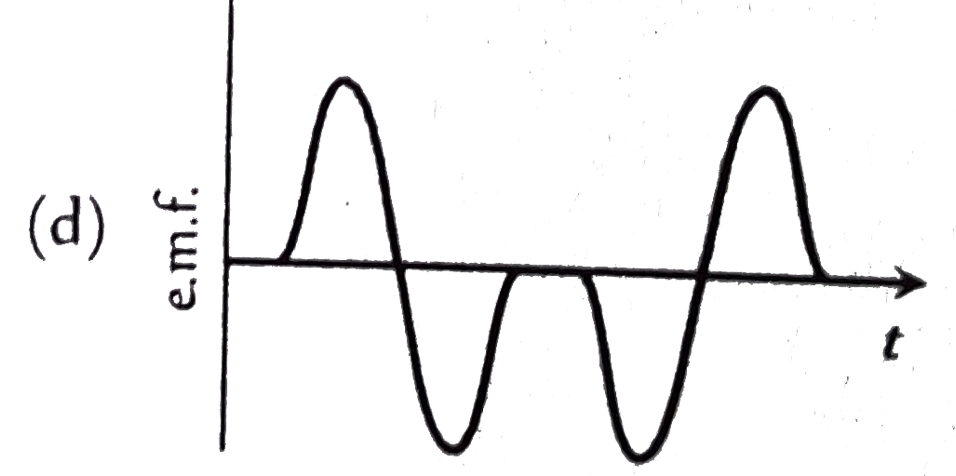
A magnet is made to oscillate with a particular frequency, passing through a coil as shown in figure. The time variation of the magnitude of e.m.f. generated across the coil during one cycle is |
|
Answer»
|
|
| 2853. |
Fora transistoramplifierthecollectorloadresistanceR_L= 2 k Omegaand theinputresistanceR_i =1 k Omega. Ifthe currentagainis 50, calculatevoltagegainof theamplifier . |
|
Answer» 100 |
|
| 2854. |
Radius of curvature of a convex mirror is 40 cm and the size of the object is twice as that of the image, then the image distance is |
|
Answer» 10 cm |
|
| 2855. |
In a series LCR A.C. circuit, by keeping resistance constant, power factor can be increased by decreasing ....... |
|
Answer» inductance cos `delta=R/Z` `therefore cos delta=R/sqrt(R^2+(X_L-X_C)^2)` `rArr` When we decrease `|X_L-X_C|` , power factor cos`delta` will INCREASE. (That is why when `X_L -X_C = 0` i. when `X_L = X_C` we have resonance in the CIRCUIT which causes MAXIMUM power transfer between source and load due to maximum power factor. |
|
| 2856. |
The Boolean expression of the output Y of the inputs A and B for the circuit shown in the fig |
|
Answer» SOLUTION :The output of AND gate 1 is `BAR(A)B` The output of AND gate 2 is `AbarB` `therefore` the output of OR gate is, `Y=barAB+AbarB` |
|
| 2857. |
A measurement of the energy DeltaE of an intermediate nucleus must be made within the mean lifetime Deltatof the nucleus and necessarily carries an uncertainty DeltaEaccording to the uncertainty principle DeltaE. Deltatt = h (a) What is the uncertainty DeltaE in the energy for an intermediate nucleus if the nucleus has a mean lifetime of 10^(-22) s? (b) Is the nucleus a compound nucleus? |
|
Answer» |
|
| 2858. |
Find the charge flown through the switch from A to B when it is closed. |
|
Answer» |
|
| 2859. |
The output of a 2-input NOR gate is fed to NOT gate, draw the logic circuit of this combination of gates and write the truth table for the output of the combination for all inputs. |
Answer» SOLUTION :
|
|
| 2860. |
In a p-n junction diode, the current I can be expressed I=I_(0) exp[(eV)/(k_T)-1] where I_(0) is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, k_ is the Boltzmann contant (8.6xx10^(-5)eV//K) and T is the absolute temperature. If for a given diode, I_(0)=5xx10^(-12)A and T=300K thenWhat will be the forward current at a forward voltage of 0.6V? What will be the increase in the current if the voltage across the diode is increased to 0.7 V? What is dynamic resistance? What will be the current if reverse bias voltage changes from 1V to 2V? |
|
Answer» Solution :Here, `I_(0)=5xx10^(-12)A, T=300K, k_(B) =8.6xx10^(-5)eVK^(-1)=8.6xx10^(-5)xx1.6xx10^(-19)JK_(-1)` If `V=0.6V`, then`(eV)/(k_T)=(1.6xx10^(-19)xx0.6)/(8.6xx10^(-5)xx1.6xx10^(-19)xx300)=23.26` `I=I_(0)[EXP((eV)/(k_T)-1)]=5xx10^(-12)[e^(23.26)-1]=5xx10^(-12)[1.259xx10^(10)-1]` `=5xx10^(-12)xx1.259xx10^(10)=0.063A` If `V=0.7V, then (eV)/(k_T)=(1.6xx10^(-19)xx0.7)/(8.6xx10^(-5)xx1.6xx10^(-19)xx300)=27.14` `I=I_(0)[exp((eV)/(k_T)-1)]=5xx10^(-12)[e^(27.14)-1]=5xx10^(-12)[6.07xx10^(11)-1]` `=5xx10^(-12)xx6.07xx10^(11)=3.035A` :. Increase in current, `DeltaI=(3.035-0.063)=2.972A` Since, `DeltaI=2.972A, DeltaV=0.7-0.6=0.1V` Dynamic resistance`=(DeltaV)/(DeltaI)=(0.1V)/(2.972A)=0.0336Omega` As the voltage CHANGES from 1 to 2 V, the current I will be almost EQUAL to `I_(0)(=5xx10^(-12)A)`, SHOWING that the diode possesses practially infinite dynamic resistance in the reverse bias. |
|
| 2861. |
The electric field intensity in a region is given by vecE=(-xhati+yhatj)V//m^2 where x, y are in meters. Then the pattern of line of forces in x-y plane is given by |
|
Answer»
|
|
| 2862. |
In figure there is graph of electric field E_(r) at point against the distance of that point from centre of the body so.... |
|
Answer» The body should be solid CONDUCTOR having ELECTRIC charge. |
|
| 2863. |
In the arrangement shown, the magnitude of each resistance is 1Omega. The equivalent resistance between O and A is given by |
|
Answer» `(14)/(13)OMEGA` |
|
| 2864. |
A spherical condenser has innder and outer spheres of radii a and b respectively. The space between the two is filled with air. The difference between the capacities of two condensers formed when outer sphere is earthed and when inner sphere is earthed will be |
|
Answer» zero |
|
| 2865. |
Drops of a liquid of density D surface tension T are floating in a liquid of density 'd' with half of the drop in the liquid, then the radius of the drop is : |
|
Answer» `SQRT((6T)/(G(2D-d)))` |
|
| 2866. |
There are three concentric thin spherical shells A, B and C of radii R, 2R, and 3R. Shells A and C are given charges q and 2q and shell B is earthed. Then which of the given is correct? |
|
Answer» CHARGE on INNER surface of SHELL C is `4/3 q` |
|
| 2867. |
The work functions of metals A and B are in the ratio 1 : 2. If light of frequencies f and 2f are incident on metal surfaces of .A and B respectively, the ratio of the maximum kinetic energies of photo electrons emitted is (f is greater then threshold frequency of A, 2f is greater than threshold frequency of B |
|
Answer» `1:1` |
|
| 2868. |
उत्तल लेंस |
|
Answer» किनारों की अपेक्षा बीच में मोटा होता है |
|
| 2869. |
A flat coil of wire has an inductance of 4.0 mH and a resistance of 5.00 omega. It is connected to a 22.0 -V battery at the instant i = 0. Consider the moment when the current is 3.00 A. (a) At what rate is energy being delivered by the battery? (b) What is the power being delivered to the resistance of the coiil ? (c) At what rate is energy being stored in the magnetic field of the coil? (d) What is the relationship among these threepower values.? (e) Is the as well? (f) Explain the relationship at the moment immediately after t = 0 and at a moment several seconds later. |
|
Answer» |
|
| 2870. |
Monochromatic green light of wavelength 500 nm illuminates a pair of slits 1 mm apart. Separation between the two consecutive bright fringes on the interference pattern formed on a screen 2 m away is |
|
Answer» 0.25mm |
|
| 2871. |
Formula of magnification of astronomical telescope is ...... |
|
Answer» `m=(f_0)/(f_e)` |
|
| 2872. |
A circular coil with radius 10 cm and 10 no. of tightly wound identical turns is kept perpendicular to uniform magnetic field 2 xx 10^(-4)G intensity. Now, it is rotated with angular velocity 2pi "rad s"^(-1) about an axis passing through it but perpendicular to magnetic field. Then, at ........s, least time magnetic flux passing through it becomes half of maximum magnetic flux. |
|
Answer» `1/2` `THEREFORE Phi=Phi_"max" cos (omegat)`…(2) (Where `Phi_"max"` = maximum magnetic FLUX passing through the coil ) Now , we are given `Phi=1/2Phi_"max"` `therefore 1/2 Phi_"max"=Phi_"max" cos (omegat)` `therefore cos (omegat)=1/2` `therefore omegat =pi/3` `therefore (2pi)t=pi/3` `therefore t=1/6s` |
|
| 2873. |
The electric field of an electromagnetic wave travelling through vacuum is given by the equation E=E_(0) sin (k x - omega t). The quantity that is independent of wavelength is |
|
Answer» a. `(K)/(OMEGA)` |
|
| 2874. |
A uniform magnetic field vec(B) fills a cylindrical volumes of radius R. A metal rod CD of length l is placed inside the cylinder along a chord of the circular cross-section as shown in the figure. If the magnitude of magnetic field increases in the direction of field at a constant rate dB//dt, find the magnetitude and direction of the EMF induced in the rod. |
|
Answer» `E=E_("induce")` `ointvec(E).vec(DL)=d/(dt)vec(B).vec(A)` `E2pir=(dB)/(dt).pir^(2)` `E=r/2 (dB)/(dt)`  `V_(D)-V_(A)=-int vec(E).dvec(x) =-intE'dx cos (pi-0)` `=int Edx COSTHETA` `V_(D)-V_(A)=1/2 intr(dB)/(dt)dx costheta=1/2 (dB)/(dt)int bdx` `=1/2 (dB)/(dt).b int_(0)^(L//2) dx=1/2(dB)/(dt)sqrt(R^(2)-L^(2)/4)xxL/2` `V_(D)-V_(C )=L/2sqrt(R^(2)-L^(2)/4)(dB)/(dt)` `V_(induced)=A(dB)/(dt)=2xx1/2xxL/2xxsqrt(R^(2)-L^(2)/4)(dB)/(dt)` `V_(induce)=L/2sqrt(R^(2)-L^(2)/4)(dB)/(dt)` 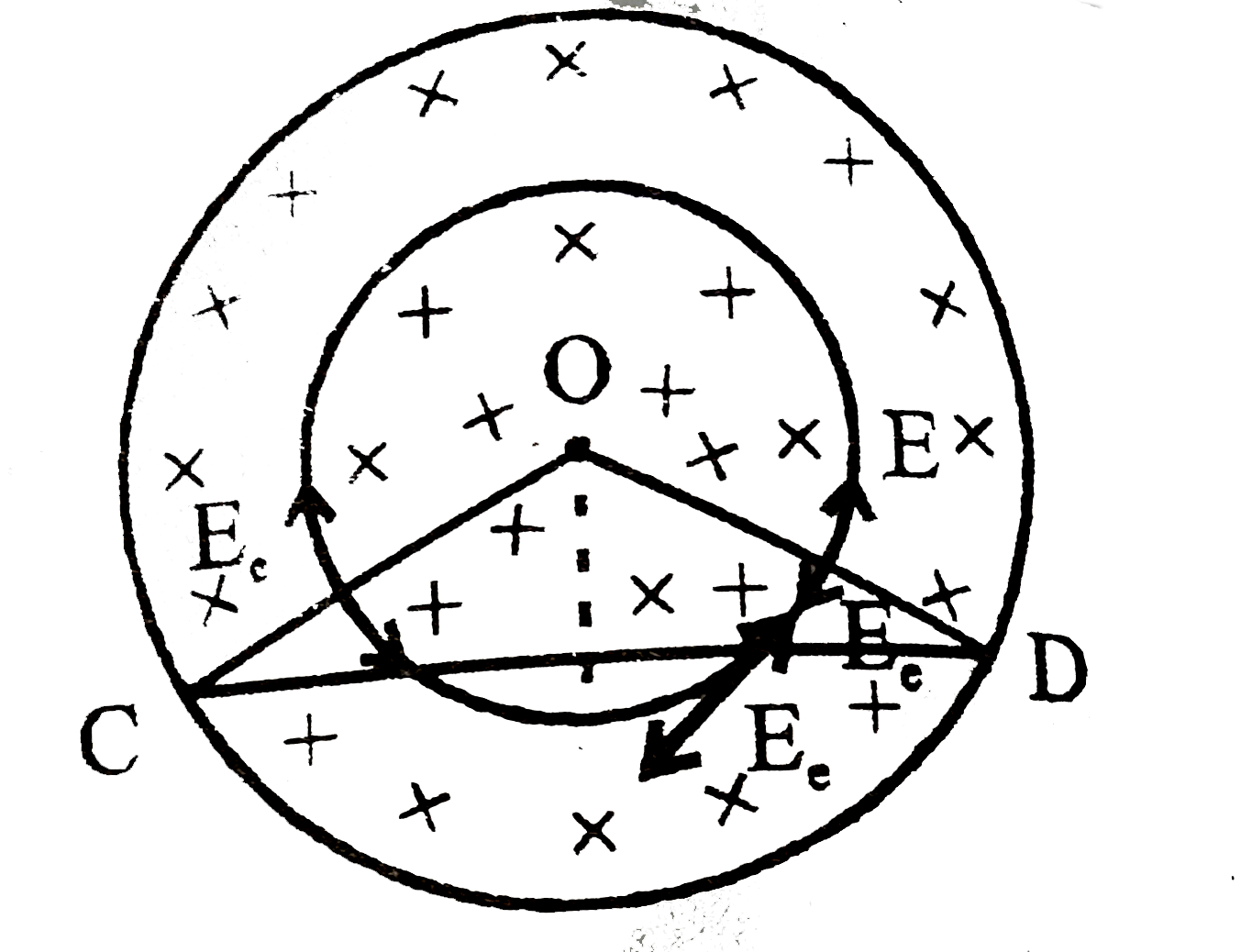 `V_(CO)+V_(DC)+V_(OC)=1/2 sqrt(R^(2)-L^(2)/4)(dB)/(dt)` `V_(CO)` and `V_(OC)` are `0`, because `E` and `dl` are `_|_` `V_(CD)=L/2 sqrt(R^(2)-L^(2)//4) (dB)/(dt)` |
|
| 2875. |
On fig. CP represents a wavefront and AO and BP, the corresponding two rays. Find the condition on theta for constructive interference at P between the ray BP and reflected ray OP : |
|
Answer» `cos theta = 3/2 (lambda)/(d)` In `DeltaOPS , OP = (PS)/(cos theta) = (d)/(cos theta)`" `(because PS = d)` In `DeltaCOP , (OC)/(OP) = cos 2 theta` `therefore` From equation (1) , we GET `Deltax = OP+ OP cos 2 theta = OP(1 + cos 2 theta)` ` = (d)/(cos theta) (1 + 2 cos^(2) theta - 1) = 2 d cos theta` 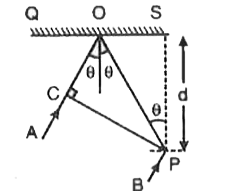 The condition of constructive interference at P is : `Deltax = (lambda)/(2) .(3lambda)/(2)`,...etc or `2d cos theta = (lambda)/(2),(3 lambda)/(2)`...etc or `cos theta = (lambda)/(4d),(3 lambda)/(4d)`...etc. |
|
| 2876. |
it is rotated through an arbitrary angle |
|
Answer» It is rotated through an arbitrary angle |
|
| 2877. |
If an open organ pipe is sounded with a tuning fork having frequency 256 Hz resonance occurred at 35 cm and 105 cm the velocity of sound is : |
|
Answer» 360 m/s `therefore (lambda)/(2) = l_(2) - l_(1 ) "" rArr lambda_(2) = 2 (105 -35) ` = 140 cm=1.4 m V - v `lambda= 256 X 1.4 = 358. 4` m/s . Hence the correct choice is (a) . |
|
| 2878. |
The flux of a alpha-particle at 2^@ is 1 x 10°, calculate the flux of alpha- particle at angle 60^(@). |
|
Answer» 0.5 `(N_(60))/(N_(2))=(sin^(4) 1^(@))/(sin^(4) 30^(@))=1.50 XX 10^(-6)` `N_(60)=N_(2) xx 1.5 xx 10^(-6)` `N_(60)=1.5` |
|
| 2879. |
In a compound microscope in normal adjustment magnification and produced by objective lens is 10 cm magnification produced by the eyepiece is 8. Magnification of microscope is ________. |
| Answer» Solution :HINT : Magnification of MICROSCOPE `m=m_(0)xxm_(e)=10xx8=80` | |
| 2880. |
A telescope has an objective of local length 50 cm and an eye piece of foal length 5 cm. The least distance of distinct vision is 25 cm. The telescope is focussed for distinct vision on a scale 200 cm away from objective. Find the magnification and tube lenght. |
|
Answer» 1, 30.2 cm |
|
| 2881. |
For a glass prism (mu=1.5) the angle of minimum deviation is equal to the angle of the prism. The angle of prism is : |
| Answer» Answer :B | |
| 2882. |
A stone is thrown upwards from the top of a tower with some initial speed and it reaches the ground in second. Now it is allowed to fall with the same initial speed downward and it reaches the ground in 1 second In how much time will it reach the ground if the stone is allowed to fall freely under gravity from the same place: |
|
Answer» `((t_1+t_2)/(2))` `h=-ut_(1)+(1)/(2)g t_(1)^(2)` `h=ut_(2)+(1)/(2)g t_(2)^(2)` `h=0+(1)/(2)g t^(2)` USING `(1)/(2) g t^(2) =(1)/(2)g t_(1) t_(2) IMPLIES t=sqrt(t_1 t_2)` |
|
| 2883. |
LEDS that can emit red, yellow, orange, etc. commercially available.How these colours are obtained in a LED. |
| Answer» Solution :DIFFERENT colours are obtained by CHANGING the concentration of arsenic and PHOSPHORS in Gallium ARSENIDE Phosphide. | |
| 2884. |
Let the end error on the LHS and RHS be equal to 1 cm. For the balance point at O, find out the % error in the value of X ? (If the end error is 1 cm from both sides then it means the correct reading will become 10 cm +1 cm from LHS and 90 cm +1 cm from the RHS) |
|
Answer» `4.2 %` |
|
| 2885. |
When orange light falls on a photo sensitive surfaces the photo current begins to flow. The velocity of emitted electrons will be more when surface is hit by |
|
Answer» RED light |
|
| 2886. |
The self inductance of a coil of 100 turns if a current of 4A produced a flux of 400 Wb is: |
|
Answer» 10H |
|
| 2887. |
The number of reference frames in our universe is "_____________". |
|
Answer» 3 |
|
| 2888. |
A block of wood of mass 0.5 kg is placed on a plane making 30° with the horizontal. If the coefficient of friction between the surfaces of contact of the body and the plane is 0.2. What force is required to keep the body sliding down with uniform velocity. |
|
Answer» Solution :Force REQUIRED to KEEP the body SLIDING down with constant velocity. Given, `m = 0.5 kg, g = 9.8 ms^(-2)` `theta = 30^(@), MU = 0.2` `F = MG(sin theta - mu cos theta) = 1.6 N` |
|
| 2889. |
A ball of mass m collides horizontally with a stationary wedge on a rough horizontal surface, in the two orientations as shown. Neglect friction between ball and wedge. Two student comment on system of ball and wedge in thses situations Saurav : Momentum of system in x-direction will change by significant amout in both cases. Rahul : There are no impulsive external forces ijn y-directions in both cases hence the total momentum of system in y-directions can be treated as conserved in both cases . |
|
Answer» SAURAV is WRONG and RAHUL is CORRECT |
|
| 2890. |
In the circuit shown there is a box and capacitance C connected to alternating power source of angular frequency of 2 rad//s. Box has power factor 1 //sqrt2 and circuit has overall power factor 1. Find the impedance of the box |
| Answer» SOLUTION :`(1)/(Csqrt2)OMEGA` | |
| 2891. |
A point source of light is placed at the centre of curvature of a hemispherical surface. The radius of curvature is r and the inner surface is completelyreflecting. Find the force on the hemisphere due to the light falling on its if the source emits a power W. |
|
Answer» Solution : The energy emitted by the source per unit time, i.e., W falls on an area ` 4PI (r^2)` at a distance r in unit time. Thus, the energy falling per  unit area per unit time is `(W/(4pi (r^2))).` Consider a small area dA at the POINT P of the hemisphere . The energy falling per unit time on it is `(WdA/ (4 pi(r^2)))`. The corresponding momentum INCIDENT on this area per unit time is ` (WdA/(4pi(r^2)c)). As the light is reflected BACK, the change in momentum per unit time, i.e.,the force on dA is (dF= (2 Wd A/ (4 pi (r^2) c)). ` Suppose the radius OP through the area dA makes an angle theta with the symmetry axis OX. The force on dA is along this radius. By symmetry, the resultant force on the hemisphere is along OX. The component of dF along OX is ` dF cos theta= (2 WdA/ (4 pi (r^2)c)) cos theta.` If we project the area dA on the plane containing the rim, the projectin is dA cos theta. Thus, thecomponent of dF along OX is, ` dF cos theta = (2W/ (4pi (r^2)c))(projection of dA).` The net force along OX ` F= (2W/ (4pi(r^2)c))(sum projection of dA).` When all the small areas dA are projected, we get the area enclosed by the rim which is (`pi (r^2). Thus, ` (F= (2W/ (4pi (r^2)c)) xx pi (r^2)= (W/2c).)` |
|
| 2892. |
The colour of rays is the property of ...... |
|
Answer» AMPLITUDE |
|
| 2893. |
A beam of unpolarised light having flux 10^(3) watt falls normally on a polarizer of cross sectional area 3xx10^(-4) m^(2) .the polarizerrotateswith an angularfrequency of 31.4 rad/s .The energy of light paaing through the polarizer rotates with an angular frequency of 3.14 rad/s .The energy of light passing through the polarozer per revolution will be |
|
Answer» `10^(-4)` JOULE |
|
| 2894. |
A cube has refractive index mu_(1) . There is a plane of refractive index mu_(2)(mu_(2) lt mu_(1)) upon it. A ray travelling through air is incident on a side face of the cube. The refracted ray is incident on the upper face of the cube at the minimum angle for total internal reflection to occur. Finaily the reflected ray emerges from opposite face. Show that if the angle of emergenceis phi then sin phi = sqrt(mu_(1)^(2) - mu_(2)^(2)). |
|
Answer» Solution :In Fig. 2.28, PQ = incident ray on the side face of the cube, QR = refracted ray inside the cube, RS = totally reflected ray from the upper face of the cube, ST = emergent ray from the opposite face. Let critical ANGLE for total reflection be `theta_(c)`. According to the question, `theta._(c) approx theta_(c)` `i.e. "" sintheta._(c) approx theta_(c) = (1)/(2^(mu)1) = (1)/((mu1)/(mu_(2))) = (mu_(2))/(mu_(1))` Angle of incidence of the ray `RS= i = 90^(@) - theta_(c)` and angle of refraction= `PHI`. `THEREFORE "" (sini)/(sinphi) ` = refractive index of air with respect to the cube `= (1)/("refractive index of the with respect to air")` `or. "" (sini)/(sinphi) = (1)/(mu_(1))` `or, " " sinphi = mu_(1)sini` `= mu_(1) sin(90^(@) - theta_(c)) = mu_(1)costheta_(c)` `= mu_(1) sqrt(1 - sin^(2)theta_(c))` `= mu_(1) sqrt((1- mu_(2)^(2))/(mu_(1)^(2))) = sqrt(mu_(1)^(2) - mu_(2)^(2))` |
|
| 2895. |
A spaceship is moving directly towards a planet at a speed of c/2. When the spaceship is 4.5xx10^(8)m from the planet (as measured by someone on the spaceship), a pulse of light is emitted by someone on the planet. As measured by someone on the spaceship, how long does it take the light pulse to travel from the planet to the ship? |
|
Answer» 0.5sec `t=(d)/(c)=(4.5xx10^(8)m)/(3.0xx10^(8)m//s)=1.5s`. |
|
| 2896. |
The error in the measurement of the radius of a sphere is 1% . The error in the measurement of its volume is : |
|
Answer» `1%` `:.(DeltaV)/(V)xx100=3(DeltaR)/(R)xx100` `=3xx1%=3%` Hence correct choice is `(b)`. |
|
| 2897. |
The Bohr model for the spectra of a H-atom (a) Will not be applicable to hydrogen in the molecular form (b) will not be applicable as it is for a He-atom (c) Is valid only at room temperature (d) predicts continous as well as discrete spectral lines. |
|
Answer» both 'a' and 'B' are true |
|
| 2898. |
The efficiency of a Carnot engine is 50% and temperature of sink is 500 K. If temperature of source is kept constant and its efficiency raised to 60%, then the required temp. of sink will be: |
|
Answer» 100 K `eta_(2)=1-(T_(2).)/(T_(1)) rArr (60)/(100) =1-(T_(2).)/(1000) rArr T_(2).=400 K` `therefore` Correct CHOICE is (C ). |
|
| 2899. |
In his first work ''On the Structure of Atoms and Molecules'' (1913) Niels Bohr, as a proof of the validity of his theory, cited the fact that the number of spectral lines of the Balmer series observed in a gas-discharge tube never exceeds 12, while 33 lines are seen in the spectra of celestial bodies. Bohr's explanation was that the diameter of the hydrogen atom cannot exceed the average interatomic distance, which depends on the pressure. From these considerations, estimate the concentration of atoms, the pressure and the density of hydrogen in a gas discharge tube and in a celestial body. |
|
Answer» `n_(0)le1/d^(3),orn_(0)le1/(8n^(6)a_(0)^(3))` Since the Balmer SERIES is excited as the result of the transition of an electron to the second level, the maximum number of the level is TWO units more than the maximum number of observed lines. Hence in a gas-discharge TUBE n = 14, in a celestial body n = 35. |
|
| 2900. |
A plate with plane parallel faces having refractiv index 1.8 rests on a plane mirror. A light ray is incident on the upper face of the plate at 60^@. How far from the entry point will the ray emerge after reflection by the mirror. The plate is 6cm thick? |
Answer» 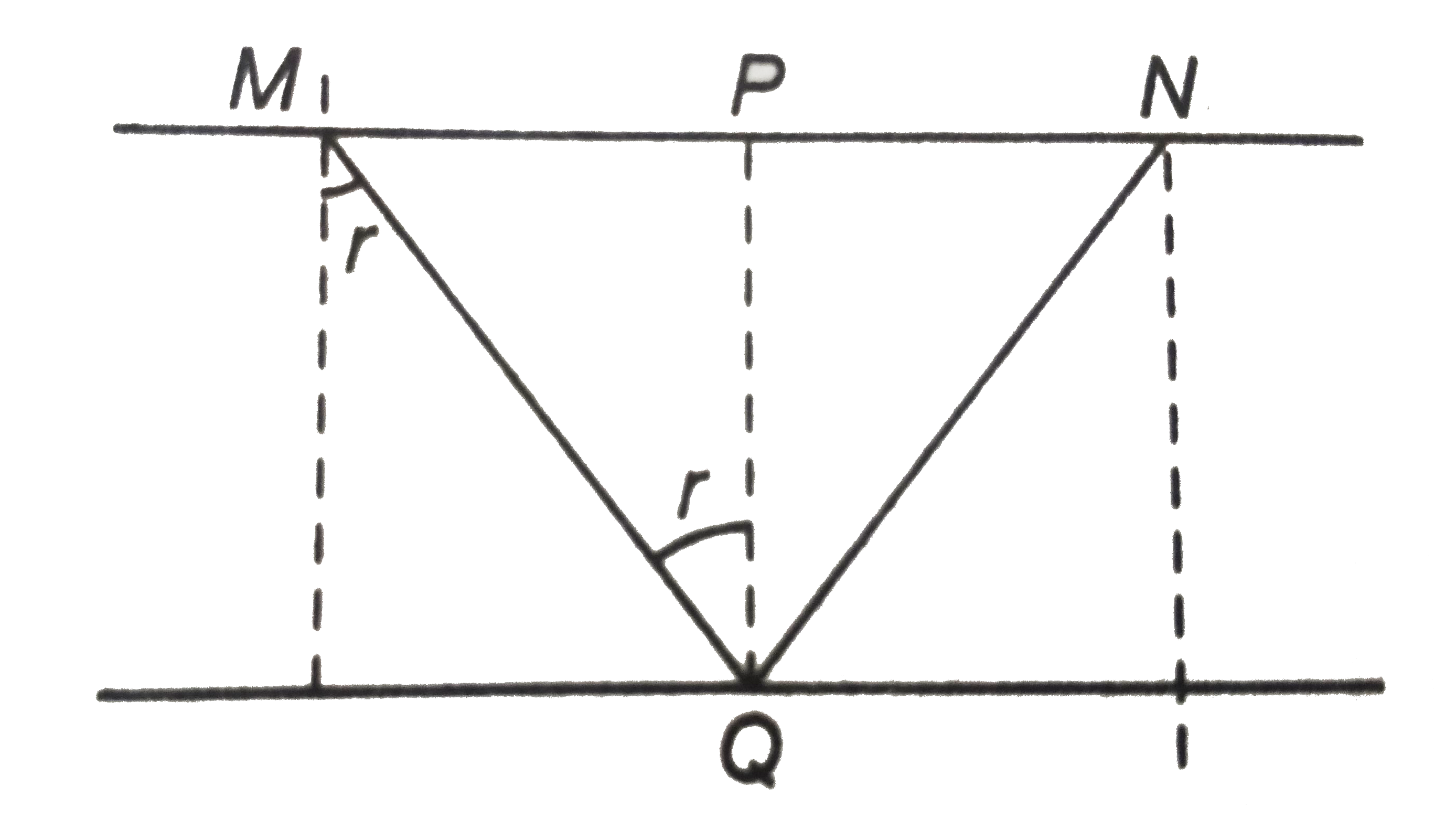 `1.8=sin60^@/sinr` Solving, we get `r=28.8^@` `MP=PQ TANR` `:. MN=2(MP)=2PQ.tanr` `=2xx6xxtan 28.8^@` `=6.6 CM` `mu=sin45^@/sinr=4/3` |
|