Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

2901.

Tweleve celles each having the same emf are connected in series and are kept in a closed box. Some of the cells are wrongly connected. This battery is connected in series with an ammeter and two cells identical with each other. The current is 3A when the cells and battery aid each other and 2A when the cells and battery oppose each other. How many cells are wrongly connected?

Answer»

Solution :Let m cells are wrongly CONNECTED in the BATTERY and `epsilon_("net")=(12-2m)epsilon`
When two cells aid the battery, the CURRENT
`3=((12-2m)epsilon+2epsilon)/(R )"……(i)"`
where R is the total resistance of the circuit. When two cells opposes the battery, then
`2=((12-2m)epsilon-2epsilon)/(R )".....(ii)"`
Solving above equations, we get `m=1`
Hence one cell is wrongly connected in the battery.
Discussion
2902.

The diameter of the nano wire is about .......

Answer»

`10^(-6)`m
`10^(-3)`m
`10^(-8)`m
`10^(-9)`m

Answer :d
Discussion
2903.

How are electromagnetic waves produces by osillating charges ? Why is it not possible to produce e.m. waves in the visible region with modern electronic circuit in the laboratory? What is the method of production of x-rays?

Answer»

Solution :When a charge q is oscillating with a FREQUENCY
v, it produces an oscillating electric field, which
in turn produces oscillating magnetic field. This
oscillating magnetic field produces oscillating
electric field and so on. This simultaneous
oscillating electric magnetic fields
produces electromagnetic wave of frequency v.
In fact electromagnetic waves are those waves
in which there sinusoidal VARIATION of electric
and magnetic field vectors at right angles to each
other as well as at right angles to the direction
of propagationof wave.
In order to produce e.m. wave in the visible region
say yellow light of frequency`6xx10^-14Hz`. For this
we have to set up an oscillatorycircuit of frequency
`6xx10^14Hz`. The MODERN electronic circuit with
LATEST techniques can hardly produce oscillates
of frequency `10^11Hz.` That is why e.m. wave in
the visible region cannot be produced with modern
electronic circuits.
X-rays are produced, when fastly moving
electrons are suddenly STOPPED by the metal
target of high atomic number.
Discussion
2904.

Who gave advice to the little kite?

Answer»

BIG kite
Birds
Boys
None of the above

Answer :A
Discussion
2905.

A dielectric sphere of radius 10 cm has a charge of 3 mC distributed uniformly throughout its volume. The dielectric constant of the material of the sphere is 1. A bullet having charge 3 mc and mass 10 g is fired from the surface of the sphere along the diameter, directly towards its centre. Assuming the sphere to be fixed and neglecting any forces other than electrostatic force, the minimum velocity of the bulge so that it can emerge from the other side of the sphere is

Answer»

`3XX10^(3) MS^(-1)`
`3xx10^6 ms^(-1)`
`9xx10^6 ms^(-1)`
`9xx10^3 ms^(-1)`

ANSWER :D
Discussion
2906.

A car starts from rest and moves with constant acceleration. The ratio of the distance covered in the nth second to that covered in n seconds is

Answer»

`2/n^2 - 1/n`
`2/n^2 -+ 1/n`
`2/n - 1/n^2`
`2/n + 1/n^2`

ANSWER :C
Discussion
2907.

A cricket ball of mass 250 g collides with a bat with velocity of 10 m/s and returns with the same velocity in 0.01s. The force acting on the bat is

Answer»

25 N
50 N
250 N
500 N

Answer :D
Discussion
2908.

Explain the term modem.

Answer»

SOLUTION :Modem performs the FUNCTIONS of both modulator and demodulator. While transmitting SIGNAL, modem ACTS as a modulator while in receiving MODE, modem acts as a demodulator.
Discussion
2909.

An air-cored solenoid is of length 0.3m, area of cross section 1.2 xx 10^(-3)m^(2) and has 2500 turns. Around its central section, a coil of 350 turns is wound. The solenoid and the coil are electrically insulated from each other. Calculate the emf induced in the coil if the initial current of 3A in the solenoid is reversed in 0.25s.

Answer»

Solution :`M= (mu_(0)N_(1)N_(2)A_(2))/(L)`
`= (4pi xx 10^(-7) xx 2500 xx 350 xx 1.2 xx 10^(-3))/(0.3)H`
`=4.4 xx 10^(-3)H`
`e= M (dI)/(dt) rArr e= 4.4 xx 10^(-3) xx (3 -(-3))/(0.25) V= 0.1056V`
If two solenoids are of unequal length, then length of bigger solenoid is to be considered.
Discussion
2910.

Unpolarised light of intensity I_0 is incident on two crossed polaroids. The intensity of light transmitted by the combination will be .............. .

Answer»


ANSWER :ZERO
Discussion
2911.

K_H …………………. With increase in temperature

Answer»

decrease
INCREASE
May increase or decrease
No effect

Answer :B
Discussion
2912.

The shape of the wavefront originating from a line source is _____ .

Answer»

SOLUTION :CYLINDRICAL
Discussion
2913.

(a) Define the term 'critical angle' for a pair of media (b) A point source of monochromatic light S is kept at the centre of the bottom of a cylinder of radius 15.0 cm. The cylinder contains water (refractive index =4/3 to a height of 7.0 cm. Drawthe ray diagram and calculate the area of water surface through which the light emerges in air.

Answer»

Solution :(a) N/A
(b) (b) The ray diagram is shown in Fig. 9.55. The light emerges in air along a circular surface of WATER of radius OB = R, where `angleOSB = i_( c)` = critical angle for wave-air INTERFACE.

Obviously, `sin i_( c) = (OB)/(SB) = R/sqrt(h^(2) + R^(2)) = 1/n`
`rArr R = h/sqrt(n^(2)-1) = (7 cm)/(sqrt((4/3)^(2))-1) = 3sqrt(7) cm`
`therefore` Area of water surface `A = piR^(2) = 22/7 XX (3sqrt(7))^(2) = 198 cm^(2)`
Discussion
2914.

Some water is placed in a container made ofa material of poor thermal conductivity. Temperature of water in it is 520 K. The total wall area of the container is 8000 cm^(2). The surrounding temperature is 300 K. Find the rate at which heat current will flow from atmosphere to water.

Answer»


ANSWER :`[440W]`
Discussion
2915.

Electron in hydrogen atom first jumps from third excited state to second excited state and then from second excited to the first excited state. The ratio of the wavelengths lambda_(1), lambda_(2) emitted in the two cases is

Answer»

`7//5`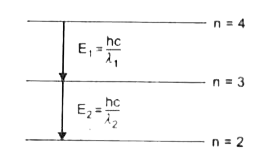
`27//20`
`27//5`
`20//7`

Solution :
`E_(1)=(hc)/(lambda_(1))=13.6 [(1)/((3)^(2))-(1)/((4)^(2))] ........(i)`
`E_(2)=(hc)/(lambda_(2))=13.6 [(1)/((2)^(2))-(1)/((3)^(2))] ......(ii)`
dividing EQ. (ii) by eq. (i)
`lambda_1/lambda_(2)=(1/4-1/9)/(1/9-1/(16))=(20)/7`
Discussion
2916.

Which of the following processes are forbidden by the law of conservation of lepton charge: (1)nrarrp+e^(_)+v, (2) pi^(+)rarrmu^(+)+e^(-)+e^(++), (3) pi^(-)rarrmu^(-)+v, (4)p+e^(-)rarrn+v, (5)mu^(+)rarre^(+)v+overset(~)v, (6) K^(-)rarr mu^(-)+overset(~)v ?

Answer»

Solution :(1) The process `nrarrp+e^(-)+v_(e )` cannot occur as there are `2` more leptons `(e^(-),v_(e ))` on the right compared to zero on the left.
(2) The process `pi^(+)RARR mu^(+)e^(-)+e^(+)` is forbidden because this corresponds to a CHANGE of lepton number by, (`0` on the left -1 on the right)
(3) The process `pi^(-)rarr mu^(-)+v_(mu)` is forbidden `mu^(-), v_(mu)` being both leptons `DeltaL=2hre`.
(4),(5),(6) are allowed (except that one MUST distinguish between muon neutrinoes and electron neutrinoes). The correct names would be
(4) `P+e^(-)rarrn+v_(e )`
(5) `mu^(+)rarre^(+)+v_(e )+overset(~)v_(mu)`
(6) `K^(-)rarr mu^(-)+overset(~)v_(mu)`.
Discussion
2917.

A gas flows with a velocity of v along a pipe of cross sectional area s and bent at angle of 90^@ at a point A. what force does the gas exert on the pipe at A if it's density is rho ?

Answer»

a)`(SQRT2 SV)//rho`
B)`(sqrt2Sv^2rho)`
c)`sqrt3Sv^2rho`
d)`sqrt3Svrho`

Answer :B
Discussion
2918.

A satellite of mass m is circulating around the earth with constant angular velocity. If radius of the orbit is r and mass of the earth M, the angular momentum about the centre of the earth is :

Answer»

`m sqrt((GM)/(R ))`
`M sqrt(Gmr)`
`M sqrt((GM)/(r ))`
`m sqrt(GM r)`

Solution :`L=mv" "FC=m sqrt((GM)/(r )).R=m sqrt(GMr)`
So the correct CHOICE is (d).
Discussion
2919.

A radio nuclide A_(1) with decay constant lamda_(1) transform into radio nuclide A_(2) with decay constant lamda_(2). Assuming that at the initial moment the preparation contained only radio nuclide A_(1), then the time interval after which the activity of radio nuclide A_(2) reaches its maximum value is

Answer»

`(LN(lamda_(2)//lamda_(1)))/(lamda_(2)-lamda_(1))`
`(ln(lamda_(2)//lamda_(1)))/(lamda_(2)lamda_(1))`
`ln(lamda_(2)-lamda_(1))`
`e^-(lamda_(1)-lamda_(2))`

Answer :A
Discussion
2920.

If yellow light of 5890 Å is incident on a grating that has 850 lines per mm. what will be the angle between both the first order images?

Answer»


ANSWER :`60^(@)`
Discussion
2921.

A plane polarized light is incident normally on a tourmaline plate. Its vecE vectors make an angle of 60^(@) with the optic axis of the plate. Find the percentage difference between initial and final intensities.

Answer»

0.25
0.75
0.5
0.9

Solution :`I=I_(0)COS^(2) THETA`
`=I_(0)cos^(2) 60^(@)`
`I=(I_(0))/(4)`
`(I_(0)-I)/(I_(0))xx100%=(I_(0)-(I_(0))/(4))/(I_(0))xx100%`
`=(3I_(0))/(4I_(0))xx100=75%`
Discussion
2922.

Number of spectral line of hydrogen atom is

Answer»

6
15
8
`OO`

SOLUTION :`oo`
Discussion
2923.

Depict the equipotential surfaces for a system of two identical positive point charges placed at distance 'd' apart.

Answer»

SOLUTION :
Discussion
2924.

In 1924, the French physicist Louis de-Broglie, suggested that moving particles of matter should display wave like properties under suitable conditions. His reasoning was that nature was symmetrical and so the two basic physical entities, matter and energy, must have symmetrical character. if radiation shows dual character so should matter. he proposed that the wavelength lamda associated with a particle of momentum p is given as: lamda=(h)/(p)=(h)/(mv) Dual aspect of matter is evident in this relation. whereas wavelength lamda is an attribute of a wave, the momentum p is a typical attribute of a particle. the Planck's constant 'h' relates the two attributes. The de-Broglie's hypothesis of matter waves has been basic to the development of medern quantum mechanics. it also led to the field of electron optics. the wave properties of electrons have been utilised in the design of electron microscope which is a great improvement, with higher resolution, over the optical microscope. Q. Why do not macroscopic particle (e.g. a moving cricket ball) show wave like properties ?

Answer»

SOLUTION :For macroscopic particles the de-Broglie wavelength is EXTREMELY small `(lamda=10^(-34)`m or even less) and is BEYOND any measurement. So they do not SHOW wave like properties in daily life.
Discussion
2925.

A block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is

Answer»

9.8 N
0.98 N
1.96 N
5 N

ANSWER :D
Discussion
2926.

In 1924, the French physicist Louis de-Broglie, suggested that moving particles of matter should display wave like properties under suitable conditions. His reasoning was that nature was symmetrical and so the two basic physical entities, matter and energy, must have symmetrical character. if radiation shows dual character so should matter. he proposed that the wavelength lamda associated with a particle of momentum p is given as: lamda=(h)/(p)=(h)/(mv) Dual aspect of matter is evident in this relation. whereas wavelength lamda is an attribute of a wave, the momentum p is a typical attribute of a particle. the Planck's constant 'h' relates the two attributes. The de-Broglie's hypothesis of matter waves has been basic to the development of medern quantum mechanics. it also led to the field of electron optics. the wave properties of electrons have been utilised in the design of electron microscope which is a great improvement, with higher resolution, over the optical microscope. Q. How can you measure the wave character of particles in subatomic domain?

Answer»

Solution :For PARTICLES of subatomic DOMAIN (e.g., electron, proton etc.), the de-Broglie wavelength is of the same ORDER as the spacing between the atomic PLANES in crystals and so we can measure de-broglie wavelength by crystal DIFFRACTION experiments.
Discussion
2927.

A plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i)andvec(B)=B_(0)sin(kz - omega t)hat(j).By using similar process and the equation int vec(B).vec(d)l = mu_(0)I+ in_(0)(d phi_(E ))/(dt), prove that c=(1)/(sqrt(mu_(0)in_(0)))

Answer»

Solution :As shown in FIGURE square loop 1234 is in yz - plane.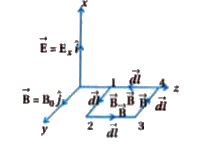

`oint VEC(B).vec(d)l=int_(1)^(2)vec(B).vec(d)l+int_(2)^(3)vec(B).vec(d)l+ int_(3)^(4)vec(B).vec(d)l+int_(4)^(1)vec(B).vec(d)l`
`= int_(1)^(2) B dl cos 0^(@)+int_(2)^(3) B dl cos 90^(@)+int_(3)^(4)B dl cos 180^(@)+ int_(4)^(1)B dl cos 90^(@)`
`= B_(0)h[sin(kz_(1)-omega t)-sin (kz_(2)-omega t)] "" [because " taking " dl = h] ""`...(3)
Now to find `phi_(0)=int vec(E ).vec(d)s` consider square loop 1234 which is made up of no. of small section of area DS = hdz.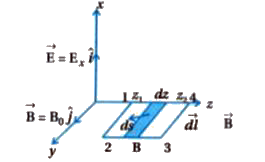

`phi_(E )=int vec(E ).vec(d)s = int Eds cos 0^(@) = int Eds "" [because cos 0^(@)=1]`
`= int_(z_(1))^(z_(2))E_(0)sin (kz_(1)-omega t)hdz`
`=-(E_(0)h)/(k)[cos (kz_(2)-omega t)-cos (kz_(1)-omega t)]`
`therefore (d phi_(E ))/(dt)=(E_(0)h omega)/(k)[sin (kz_(2)-omega t)-sin (kz_(1)-omega t)] ""` ...(4)
From Ampere law,
`oint B dl = mu_(0)(I_(c )+in_(0)(d phi_(E ))/(dt))`
where `I_(c )` is conduction current for vacuum `I_(c )= 0`
HENCE,`oint B dl=(mu_(0)in (d phi_(E ))/(dt))`
From equation (3) and (4),
`B_(0)h[sin (kz_(1)-omega t)-sin (kz_(2)-omega t)]`
`= mu_(0)mu_(0)(E_(0)h omega)/(k)[sin (kz_(1)-omega t)-sin (kz_(2)-omega)]`
`therefore B_(0) = (mu_(0)in_(0)E_(0)omega)/(k)`
`therefore (1)/(mu_(0)in_(0))=(E_(0)omega)/(B_(0)k)`
`therefore (1)/(mu_(0)in_(0))= c xx (ck)/(k)[because (E_(0))/(B_(0))=c " and " omega = ck]`
`therefore (1)/(mu_(0)in_(0))=c^(2)`
`therefore c=(1)/(sqrt(mu_(0)in_(0)))`
Discussion
2928.

Consider a beam of electrons (each electron with energy E_(0)) incident on a metal surface kept in an evacuated chamber. Then

Answer»

no electrons will be EMITTED as only photons can emit electrons
electrons can be emitted but all with an energy `E_(0)`
electrons can be emitted with any energy, with a maximum of `E_(0) - PHI` (`phi` is the work FUNCTION)
electrons can be emitted with any energy, with a maximum of `E_(0)`

Answer :D
Discussion
2929.

In order to decrease radioactive nuclei to one million of its initial number, number of half - lives required is

Answer»

20
40
40
10

Answer :A
Discussion
2930.

In 1924, the French physicist Louis de-Broglie, suggested that moving particles of matter should display wave like properties under suitable conditions. His reasoning was that nature was symmetrical and so the two basic physical entities, matter and energy, must have symmetrical character. if radiation shows dual character so should matter. he proposed that the wavelength lamda associated with a particle of momentum p is given as: lamda=(h)/(p)=(h)/(mv) Dual aspect of matter is evident in this relation. whereas wavelength lamda is an attribute of a wave, the momentum p is a typical attribute of a particle. the Planck's constant 'h' relates the two attributes. The de-Broglie's hypothesis of matter waves has been basic to the development of medern quantum mechanics. it also led to the field of electron optics. the wave properties of electrons have been utilised in the design of electron microscope which is a great improvement, with higher resolution, over the optical microscope. Q. An electron is accelerated by applying a potential difference of 100 volt. calculate its de-Broglie wavelength.

Answer»

SOLUTION :de-Broglie wavelength of ELECTRON `lamda=(h)/(p)=(h)/(SQRT(2mK))=(h)/(sqrt(2meV))=(1.227)/(sqrt(V))NM`
As `V=100V,` hence `lamda=(1.227)/(sqrt(100))=0.1227nm` .
Discussion
2931.

A plane progressive wave is given by, y =2 cos 6.284 (330 t -x). What is the period of wave?

Answer»

`1/330 s`
`2pi XX 330 s`
`(2 PI xx 330)^(-1)s`
1

Solution :The GIVEN equation of a plane PROGRESSIVE wave is `y = 2 cos 6.284 (330t -x)`
`=2 cos 2pi (330t -x)`..........(i)
The standared equation of a plane progressive wave is
`y = A cos 2pi (t/T-x/lambda)`.........(ii)
Comparing (i) and(ii), we get
`1/T = 330` or `T = 1/330 s`
Discussion
2932.

Angular momentum of a body changes by 100 kgm^2/s , when its angular velocity changes from 25 rad/s to 50rad/s . then M.I. of the body about the axis of rotation

Answer»

`2500 kgm^2`
` 4 kgm^2`
`2 kgm^2`
`5000 kgm^2`

ANSWER :B
Discussion
2933.

A magnetic field B is confined to a region rle a and points out of the paper (the z-axis), r = 0 being the centre of the circular region. A charged ring (charge Q) of radius b, b gt a and mass m lies in the xy-plane with its centre at the origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time Deltat. Find the angular velocity omega of the ring after the field vanishes.

Answer»

Solution :In `Deltat` time flux linked with ring becomes zero from its maximum VALUE which induces emf in ring electric field is also induced in ring.
Induced emf = Electric field x `(2pib) [ because V=Ed]`
But induced emf `EPSILON=(Deltaphi)/(Deltat)=(pia^2B-0)/(Deltat)=(Bpia^2)/(Deltat)`
`therefore (Bpia^2)/(Deltat)=F(2pib)`
`therefore E=(Ba^2)/(2bDeltat)`
Force produced on ring `F=QE=(QBa^2)/(2bDeltat)`
Torque produced on ring ,
`T= rF sin theta =(b Q Ba^2)/(2bDeltat)=(QBa^2)/(2Deltat)`
Now torque = RATE of change in angular momentum,
`tau=(DELTAL)/(Deltat)`
`=(mvb-0)/(Deltat)`
`(QBa^2)/(2Deltat)=(mb^2omega)/(Deltat)`
`therefore omega=(QBa^2)/(2mb^2)`
Discussion
2934.

An object is placed 100 cm from a plane mirror how far is the image from the object?

Answer»

50cm
100cm
200cm
300cm

Solution :A plane mirror forms an IMAGE that is the same DISTANCE as the OBJECT is from a mirror, but behind the mirror. The distance from the image to the object is equal to the distance of the object to the mirror (100 CM) and the mirror to the image (100 cm). 100cm+10cm=200cm.
Discussion
2935.

A galvanometer has a resistance of 98Omega. If 2% of the main current is to be passed through the meter what should be the value of the shunt?

Answer»

SOLUTION :`G=98Omega,(i_(g))/ixx100=2%`
`s=G/((i/(i_(g))-1)),thereforei/(i_(g))=100/2=50thereforeS=98/((50-1))=2OMEGA`
Discussion
2936.

Two conductors each of length 12 m lie parallel to each other in air. The centre to center distance between the conductor in 15 xx 10^(-2) m and the current in each conductor is 300 amperes. Determine the force in newton tending to pull the conductors together.

Answer»

Solution :Force between two conductors is given by
`F = (mu_0)/(2PI) (i_1 i_2l)/(r)`
Given L = 12 m , `r = 15 XX 10^(-2) m`.
`i_1 = i_2 = 300 A`
`therefore F = 2 xx 10^(-7) xx (300 xx 300 xx 12)/(15 xx 10^(-2)) = 1.44 N`.
Discussion
2937.

A tuning fork gives 5 beat/second with another fork of 500hz .when the fork is loaded then the frequency of the ist fork.

Answer»

Solution :`n_1 = n_2 +- 5 = 500 +-5 =` 505Hz or 495Hz
when `n_1` is LOADED its FREQUENCY decreases and given that beat frequency remains unchanged. This is POSSIBLE only when `n_1` = 505Hz.
Discussion
2938.

Fig. reprensts a crystal unit of cesuim chloride, CsCl. The cesium atoms, represented by open circles are situated at the corners fo a cubeof side 0.40 mm, whereasa CI atom us situated at the centers of the cube. The Cs atoms are deficient in one electron while the CI atom carriesan excess electron. (i) What is the net electric field on the CI atom due to eightCs atoms ? (ii) Suppose that the Cs atom at the cornerA is missing. What is the net forcenow on the CI atom due to sevenremaning Cs atoms ?

Answer»

Solution :(i) Fig, Chiloine atom at the center of the CUBE is attractedequally by eightcesiumatoms at the eightcorners of the cubeSymmetry showsthat theseforceswouldcancelout in PAIRS. Therefore, net ELECTRICFIELD on CI atm dueto eightCs atoms is zero.
(ii) Removing a Cs atom at the cornerA is equivalentto addinga singlychargednegative Cs ion at A. Net force on the CIatom at A would be `F = (e^(2))/(4PI in_(0) r^(2))`, where r = distancebetween CI iion and Cs ion, i.e,
`r = sqrt((0.20)^(2) + (0.20)^(2) + (0.20)^(2)) xx 10^(-9) m = 0.346xx10^(-9) m`
`F = (e^(2))/(4pi in_(0) r^(2)) = (9xx10^(9) (1.6xx10^(-19))^(2))/((0.346xx10^(-9))^(2)) = 1.92xx10^(-9) N`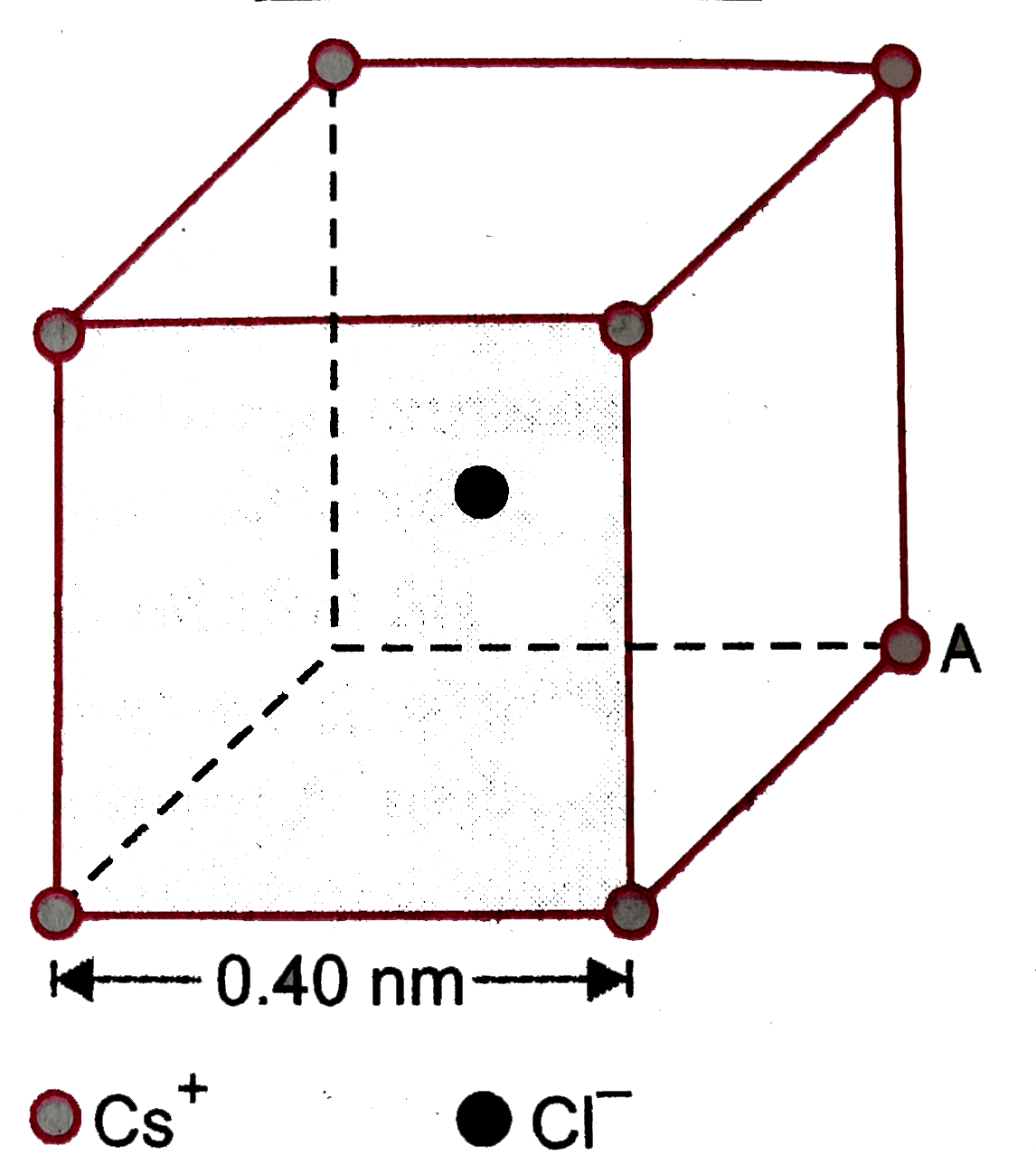
Discussion
2939.

What should be the orientation of a magnetic dipole in a uniform magnetic field so that its potential energy is maximum ?

Answer»

Solution :The orientation of dipole should be antiparallel to the MAGNETIC FIELD `vecB`. In that orientation, `U_("MAX") = +MB`
Discussion
2940.

What should be the orientation of a magnetic dipole in a uniform magnetic field so that its potential energy is minimum (or the dipole is in stable equilibrium) ?

Answer»

Solution :PARALLEL to the DIRECTION of MAGNETIC field `vecB `( i.e. , `theta= 0^@`) . In that orientation , `U_("min") =-mB`.
Discussion
2941.

A metal bar of length l is well lagged with some non-conducting material to prevent losses of heat from its surface and the two ends are maintained at steady temperatures theta_(1) and theta_(2) with theta_(1) gt theta_(2), then in the steady state the temperature theta of s section of the bar at distance x from the hot end varies as shown in the graph

Answer»




ANSWER :B
Discussion
2942.

The resistance of a wire is 5Omega at 50^(0)C and 6Omega at 100^(0)C. The resistance of the wire at 0^(0)C will be

Answer»


ANSWER :4
Discussion
2943.

Age of earth is 4 to 5 billion years . Geologists believe thant during this period earth's magnetism has changed , even reversed its direction several times . How can geologists know about earth's field in such distant past?

Answer»

Solution :The magnetic field of earth GETS WEAKLY recorded on some rocks during their SOLIDIFICATION . GEOLOGISTS trace the geomagnetic history of earth by analysing these rocks .
Discussion
2944.

When an object is moved along the principle axis of a concave mirror placedin air, the image coincides with the object if the object is 50 cm from the mirror. If the mirror is placed at a depth of 20 cm in a transparent medium, the image coincides with the object when the object is 40 cm from the mirror. The refractive index of the liquid is

Answer»

`(5)/(4)`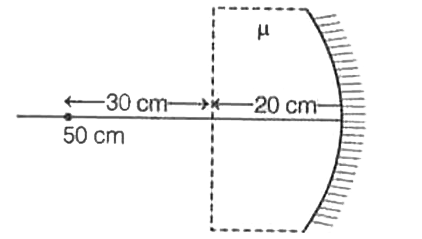
`(4)/(3)`
`(3)/(2)`
`(5)/(3)`

SOLUTION :According to the question, an object is placed on the principle axis of a CONCAVE mirrot is SHOWN in the figure below,

Since, it is given that, an object at 50 cm from pole is act like, it placed at 40 cm from the pole when mirror is placed inside a transparent medium.
`rArr v_("real") = 50 cm` and `v_("apparent") = 40 cm`
Now, distance outside the transparent medium, `D_("real") = v_("real")` - thickness of transparent medium,
`D_("real") = 50 cm - 20 cm = 30 cm`
Similarly, `D_("apparent") = (40 - 20) cm = 20 cm`
Hence, the refractive index of the LIQUID,
`mu = (D_("ACTUAL"))/(D_("apparent")) = (30)/(20) = (3)/(2)`
`:.` Hence, the correct option is (C ).
Discussion
2945.

Intensity of two sources are different and waves emitting from source experience interference. If ratio of maximum and minimum intensity in interference is 25, intensity of sources is .......

Answer»

`5:1`
`9:4`
`25:16`
`25:1`

SOLUTION :`(I_(max))/(I_(min))=(25)/(1)` but `I_(max) prop (A_(1)+A_(2))^(2)`
`:. ((A_(1)+A_(2))^(2))/((A_(1)-A_(2))^(2))=(25)/(1)` but `I_(min) prop (A_(1)- A_(2))^(2)`
`:. (A_(1)+A_(2))/(A_(1)-A_(2))=(5)/(1)`
Taking componendo- dividendo `(A_(1))/(A_(2))=(3)/(2)` `:. (I_(1))/(I_(2))=(9)/(4)`
Discussion
2946.

The color code for a resistor of resistance 3.5 K Omega with 5% tolerance is:

Answer»

ORANGE, GREEN, orange and gold
RED, YELLOW, BLACK and gold
orange, green, red and silver
orange, green, red and gold

Answer :D
Discussion
2947.

In a metre bridge the null point is found at a distance of 35 cm from A. If now a resistance of 10Omega is connected in parallel with S, the null point occurs at 50 cm. Determine the values of R and S.

Answer»

Solution :From the first balance point, we get
`(R)/(S)`=`(35)/(65)`=`(7)/(13)`…….(1)
After S is connected in parallel with a resistance of `10Omega`, the resistance across the gap CHANGES from S to`S_(EQ)`where
`S_(eq)`=`(10xxS)/(10+S)`
and hence the new balance condition now gives
`(R)/(S_(eq))`=`(R(S+10))/(10S)`=`(50)/(50)`=1….(2)
by EQUATION (1) & (2) we get S=`(60)/(7)Omega`, R=`4(8)/(13)Omega`
Discussion
2948.

A plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i)andvec(B)=B_(0)sin(kz - omega t)hat(j).Evaluate int vec(E ). Vec(d)l over the rectangular loop 134 shown in figure.

Answer»

Solution :Consider FIGURE given below,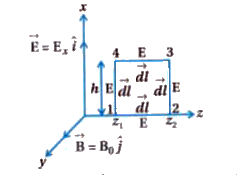

ELECTROMAGNETIC waves are propagating in z - direction.Let electric field vector `vec(E )` and `vec(B)` is in x - direction and magnetic field vector is in y - direction.
`therefore vec(E ) =E_(0)hat(i)`and`vec(B)=B_(0)hat(j)`
As shown in figure line INTEGRATION over square path 1234,
`oint vec(E ). vec(d)l = int_(1)^(2)vec(E ).vec(d)l+ int_(2)^(3)vec(E ).vec(d)l+int_(3)^(4)vec(E ).vec(d)l`
`= int_(1)^(2) Ed l COS 90^(@)+int_(2)^(3)Edl cos 0^(@)+int_(3)^(4)Edl cos 90^(@)+int_(4)^(1)Edlcos 180^(@)`
`therefore oint vec(E ).vec(d)l=E_(0)h "" [sin (kz_(2)-omega t)-sin(kz_(1)-omega t)] ""`....(1)
Discussion
2949.

If vecA, vecB, vecC are the three vectors the angle between vecA,vec B is alpha, vecB and vecC is B and C and A is y, and k is constant then match the following. {:("List-I", "List-II"),((a)A,(1) k sin alpha),((B),(2) k sin gamma),((C),(3) k sin beta):}

Answer»

a-1,b-2,C-3
a-1,b-3,c-2
a-3,b-2,c-3
a-2,b-3,c-1

Answer :C
Discussion
2950.

In a resonance column apparatus, first resonance is obtained when the water filling beaker (of cylindrical shape) is just empty as shown The water filling beaker is lowered down andit is seen that second resonance is obtained when beaker is filled upto brim. If the tunning fork has a frequency 420 Hz What is the velocity (in m//s) of sound in air ?

Answer»


SOLUTION :`pixx2^(2)xxy=pixx4^(2)XX100`
`y=40cm = lambda//2`
`lambda=80 CM`
`0.8xx420=336m//s`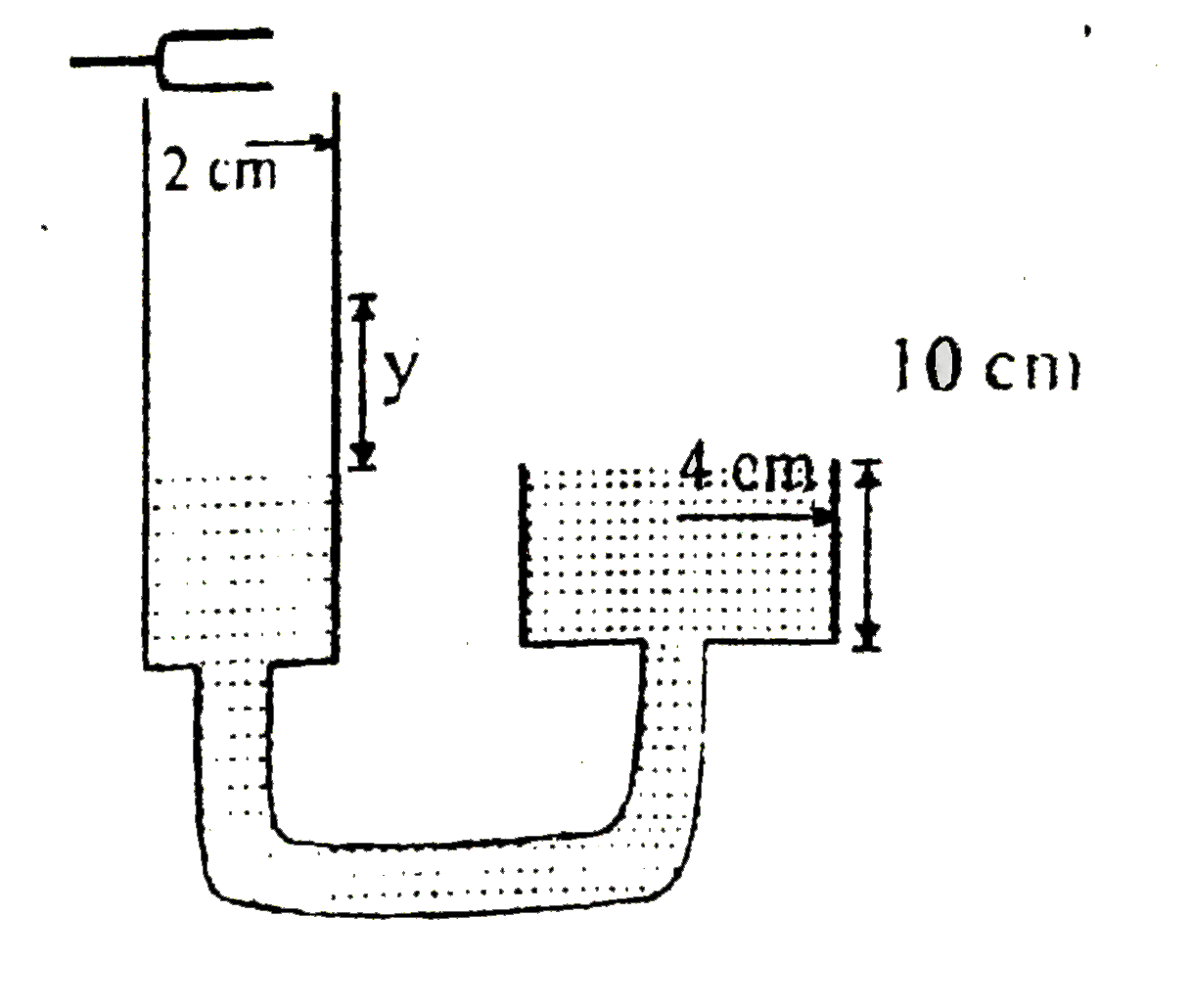
Discussion