Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3001. |
A bar magnet of length 7cm breath 2cm , thickness 1 mm , is subjected to a field of 700A/m Given susceptibility is 549 ., calculate mu_r,mu flux density |
|
Answer» |
|
| 3002. |
The frequency of oscillations of a small magnet in a magnetic field of induction 2.4xx10^-4 Wb//m^2 is n. If the frequency of oscillations of same magnet becomesn/4. What is the value of new magnetic field ? |
|
Answer» SOLUTION :`N=1/(2pi)sqrt((MB)/1)` `thereforen_1/n_2=sqrt(B_1/B_2)` `n/(n//4)=sqrt(B_1/B_2)` `THEREFORE 4^2=B_1/B_2.` |
|
| 3004. |
A satellite of mass m revolves around the earth of radius R at a height x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is |
|
Answer» gx `:. (GMm)/((R+x)^(2))=(mv_(0)^(2))/((R+x)) RARR (GM)/((R+x))=v_(0)^(2)` `rArr v_(0)^(2)=(GM)/((R+x))=(R^(2)g)/((R+x)) rArr v_(0)=[(gR^(2))/((R+x))]^(1//2)` |
|
| 3005. |
Helmholtz coils consist of two thin flat coils placed as shown in Fig. 27.6. Compare the magnetic field intensities in the centre of each coil with that in the midpoint of the axis and prove that inside the Helmholtz coils the field is almost uniform. Take the distance between the coils to be equal to one half of the radius. |
|
Answer» The field induction at the midpoint is `B_(m)=(2mu_(0) iwa^2)/(2(a^2+a^2//16)^(3//2))=(0.913mu_(0) iw)/(a)` It may be SEEN that with a SMALL error `delta` the field is almost uniform. `delta=(B_(m)-B_(c))/(B_(m))=(0.913-0.858)/(0.913)=6%` |
|
| 3006. |
Find out the value of x so that the image is formed on the object itself. |
|
Answer» Solution :CASE I : When the lens FORMS the image on the pole of the mirror `1/f=1/v-1/u` `rArr 1/10=1/30-1/(-X)` `rArr 1/x =1/10-1/30` `rArr x=15` cm Case II : When the lens forms the image on the centre of curvature of the mirror `1/20+1/x=1/10` `rArr 1/x=1/10-1/20` `:. x=20` cm |
|
| 3007. |
Derive an expression for the force acting on a current carrying conductor placed in a uniform magnetic field. Name the rule which gives the direction of the force. Write the condition for which this force will have (i) maximum (ii) minimum value. |
|
Answer» Solution :Consider a current conductor of length l and cross-section area A. If n be the free electron density for the metal of conductor then TOTAL number of free electrons in n A l. For a steady current I in the conductor, let each free electron has an average drift `vecv_d` velocity in the presence of a MAGNETIC field `vecB` HENCE, Lorentz magnetic force on a mobile electron is `VECF = -e (vecv_d xx vecB)` `:.` Force on all the mobile/free electrons of the conductor `vecF = vecf cdot n A l = - n A l e (vecv_d xx vecB)` `= I (vecl xx vecB) "" [ :. I = - n A e vecv_d]` Direction of the force is given by Fleming.s left hand rule. If magnetic field `vecB` makes an angle `theta` from the conductor then magnitude wise `F = I l B sin theta` (i) The force will have a maximum value `F_("max") = I l B` when `theta = 90^@ and sin theta = 1` (II) The force will have a zero value, when `theta= 0^@` or `180^@` and `sin theta = 0`. 
|
|
| 3008. |
A : At the first glance, the top surface of the Morpho butterfly.s wing appears a beautiful blue-green. If the wing moves the colour changes. R : Diffraction pigments in the wing reflecting at different angles. |
|
Answer» Both A and R are true and R is the correct EXPLANATION of A |
|
| 3009. |
A working transistor with its three legs marked P, Q and R is tested using a multimeter. No conduction is found between P and Q. By connecting the common (negative) terminal to P and Q, some resistance is seen on the multimeter. Which of the following is true for the transistor? |
|
Answer» <P> It is an npn TRANSISTOR with R as base |
|
| 3010. |
The surface of a metal is illuminated with the light of 400 nm. The kinetic energy of the ejected photoelectrons was found to be 1.68 eV. The work function of the metal is (hc = 1240 eV nm) |
|
Answer» 3.09 eV `= (1240)/(400) - 1.68 = 3.10 - 1.68 = 1.42` eV |
|
| 3011. |
(i) Derive the expression for electricfield at a pointon the equatorial line of an electric dipole. (ii) Depiet the orientationof the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field. |
|
Answer» Solution :(i) Let an ELECTRICDIPOLE AB of 2 point charges - q andq be separated by a smalldistance`= 2a`,with centre at O. `PO = r`. In rt. `DELTAPOA`, `AP^(2) = OA^(2) + PO^(2)` `AP^(2) = a^(2) + r^(2)` Similarly, `BP^(2) = a^(2) + r^(2)` Let`E_(1)` be the electric fieldintensity at Pdue to charge `+q` at B, then, 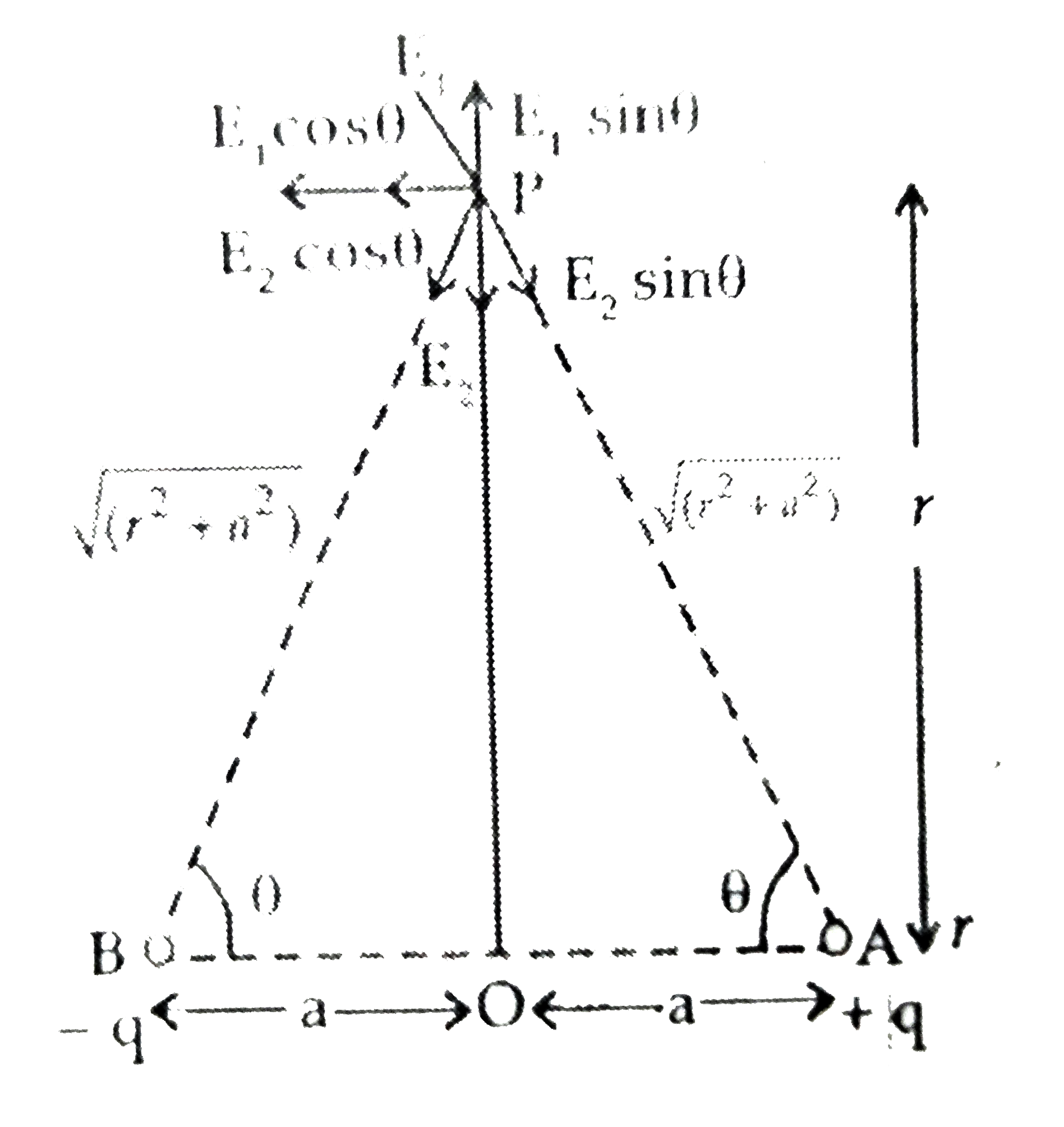 `vec(E_(1)) = 1/(4piepsi_(o)) xx(q)/((r^(2) + a^(2)))`towards PA and `vec(E_(2)) = (1)/(4piepsi_(0)) xx(q)/((r^(2) xx a^(2)))` towards BP CLEARLY, `(E_(1)) = (E_(2))` `vec(E_(1))` and `vec(E_(2))` has two rectangularcomponents, `E_(1) sin theta` towards PE and `E_(2) cos theta` towards PR and `E_(2) sin theta`towards `PF` and `E_(2) cos theta` towards PR. `E_(1) sin theta` and `E_(2) sin theta` cancel out. `rArrE_("net") = E_(1)cos theta + E_(2) cos theta = 2E_(1) cos theta` `E_("net") = 2 xx 1/(4piepsi_(o)) xx (q)/((r^(2) +a^(2))^(2)) xx q/(SQRT(r^(2) + a^(2)))` `E_("net") = (vec(P))/(4piepsi_(o)(r^(2) + a^(2))^(3//2))` (ii) In stable equilibrium, `theta = 0^(@) pE sin theta= 0` Net force `qE - qE = 0`  In UNSTABLE equilibrium , `theta = 180^(@)` Net force `= qE - qE= 0` `rArr tau = pE 180^(@) = 0` |
|
| 3012. |
A massless rod hinged at one end free to rotate in vetical plane has a bob of mass m attached to it. Bob is given a velocity v_(0) at the bottom most point. Choose the correct curves from the below options (v_(0)=sqrt(5gL)) |
|
Answer»
`impliesK=2mgL"COS"^(2) (THETA)/2+(mgL)/2` `T=6mg"cos"^(2)(theta)/2` `a_(F)=g+4g"cos"^(2)(theta)/2` `a_(t)=gsin theta =g sqrt(1-cos^(2)theta)` `impliesa_(t)^(2)=g^(2)-g^(2)cos^(2)theta` |
|
| 3013. |
Two parallel rays are travelling in a medium of refractive index mu_(1)=4//3. One of the rays passes through a parallel glass slab of thickness t and refractive index mu_(2)=3//2. The path difference between the two rays due to the glass slab will be |
|
Answer» 4t/3 |
|
| 3014. |
There are three concentric metallic spherical shells of radius R, 2R and 3R. Charge Q is given to the innermost spherical shell. If the innermost spherical shell is connected with a metal wire to the outermost spherical shell without touching the middle shell, which is connected to the earth, then, find charges appearing on all surfaces. |
Answer» Solution :If we read the question carefully then we get to know that charge distribution is to be done in a way that NET charge outermost spheres TOGETHER is Q, and electric potential of middle sphere is equal to zero because it is connected to the earth.  Let us start with the innermost sphere. There should not be any charge on INNER surface of this sphere because there is no electric field inside it. Let us assume that `q_(1)` charge appears on outer surface of the innermost sphere then we know that charge on inner surface of middle sphere of has to be `-q_(1)` DUE to electrical constraint of metallic surfaces facing each other. Now we know that the middle sphere is connected to the earth. Hence, it is not isolated. Let us assume that `q_(2)` charge appears on the outer surfaceof the middle sphere, then again due to electrical constraint charge on inner surface of outermost sphere has to be `-q_(2)`. Now charge on the outer surface of the outermost sphere is `(Q-q_(1)+q_(2))` so that the totalcharge on innermost and outermost spheres together remains Q. Electric potential of the innermost sphere is equal to the outermost sphere because thetwo are connected to each other by a metallic wire so charge on them mustensure same potential on them. We get the following equation: `V_("inner-most")=V_("outer-most")` `(q_(1))/(4pi epsilon_(0)(R ))+(q_(2)-q_(1))/(4pi epsilon_(0)(2R))+(Q-q_(1))/(4pi epsilon_(0)(3R))` `=(q_(1))/(4pi epsilon_(0)(3R))+(q_(2)-q_(1))/(4pi epsilon_(0)(3R))+(Q-q_(1))/(4pi epsilon_(0)(3R))` `rArr 6q_(1)+3q_(2)-3q_(1)=2q_(1)+2q_(2)-2q_(1)` `rArr 3q_(1)=-q_(2) rArr q_(1)= -(q_(2))/(3)"" ...(i)` The middle sphere is earthed and hence its electrical potential is zero. We get the followingequation: `V_("middle-sphere")=(q_(1))/(4pi epsilon_(0)(2R))+(q_(2)-q_(1))/(rpi epsilon_(0)(2R))+(Q-q_(1))/(4pi epsilon_(0)(3R))=0` `rArr (q_(2))/(4pi epsilon_(0)(2R))+(Q-q_(1))/(4pi epsilon_(0)(3R))=0` `rArr 3q_(2)+2Q-2q_(1)=0` `rArr 2q_(1)-3q_(2)=2Q "" ...(ii)` Now substituting value of `q_(1)` from equation (ii) we get the following: `rArr 2((-q_(2))/(3))-3q_(2)=2Q rArr (2q_(2))/(3)+2q_(2)= -2Q` `rArr (11)/(3) q_(2)= -2Q rArr q_(2)= -(6)/(11)Q "" ...(iii)` Substituting value of `q_(2)` from equation (iii) in equation (i) we get the following: `rArr q_(1)=(2)/(11)Q "" ...(iv)` Now the charge on outer surface of the outermost sphere can be written as: `Q-q_(1)+q_(2)` `Q-q_(1)+q_(2)=Q-(2)/(11)Q-(6)/(11)Q=(3Q)/(11)`. Now we have CHARGES on all surfaces. Charge on inner surface of the innermost sphere: 0 Charge on outer surface of the innermost sphere: `2Q//11` Charge on inner surface of the middle sphere: `-2Q//11` Charge on outer surface of the middle sphere: `-6Q//11` Charge on inner surface of the outermost sphere: `6Q//11` Charge on outer surface of the outermost sphere: `3Q//11` |
|
| 3015. |
The distance of the closest approach of an alpha particle fired at a nucleus with kinetic energy K is r_(0)The distance of the closest approach when the alpha particle is fired at the same nucleus with Kinetic Energy 2k will be |
| Answer» ANSWER :C | |
| 3016. |
In Above question how many fringes will cross through the centre if an ideal paper piece is pasted on the other slit also ? the wavelength of light used is 600 nm. |
|
Answer» Solution : Number of fringes crossed through centre `=Y_0/beta=(((MU-)TD)/d)/((Dlamda)/d)=((mu-)t)/lamda` `=(9times10^-6)/(600 times10^-9)=15` |
|
| 3017. |
In between two rational number there is/are: |
|
Answer» Exactly one RATIONAL number |
|
| 3018. |
A simplependulum performs simple harmonic motion about x = 0 with an amplitude a and time period T. The speed of the pendulum at x=(a)/(2) will be : |
|
Answer» `(PIA)/(T)` `:.""v=omega sqrt(a^(2)-(a^(2))/(4))=omega sqrt((3a^(2))/(4))` `=(2PI)/(T)(a sqrt(3))/(2)=(pi a sqrt(3))/(T)` Correctchoice is ( c ). |
|
| 3019. |
If vec A and vec B are two vectors can vec A + vec B be equal to zero ? |
| Answer» Solution :`VEC A + vec B` MAY be zero when `vec A` and `vec B` are opposite VECTORS i.e. when they have same magnitude but in opposite direction . | |
| 3020. |
Name the instrument which is used to measure potential difference. |
| Answer» SOLUTION :POTENTIOMETER | |
| 3021. |
What kind of polarizations has a plane electromagetic wave if the projections of the vector E on the x and y axes are perpendicular to the propagation direction and are defind by the following equations: (a) E_(x) = Ecos (omegat - kz), E_(y) = E sin (omegat - kz), (b) E_(x) = E cos(omegat - kz), E_(y) = E cos (omegat - kz + pi//4) (c) E_(x) = E cos (omega t - kz), E_(y) = E cos (omega t - kz + pi)? |
|
Answer» Solution :The wave is moving in the direction of `z`-axis (a) Here `E_(x) = E cos (omegat - kz), E_(y) = E sin(omegat - kz)` `(E_(x)^(2))/(E^(2)) + (E_(y)^(2))/(E^(2)) = 1` so the up of the electric vector moves along a circle. For the right handed coordinate system this represents circular anticlockwise POLARIZATION when observed towards the incoming wave. (b) `E_(x) = E cos (omegat - kz), E_(y) = Ecos (omegat - kz+(PI)/(4))` so `(E_(y))/(E) = (1)/(SQRT(2)) co s(omegat - kz) - (1)/(sqrt(2)) sin (omegat - kz)` or `((E_(y))/(E) - (1)/(sqrt(2))(E_(x))/(E))^(2) = (1)/(2)(1-(E_(x)^(2))/(E^(2)))` or `(E_(y)^(2))/(E^(2)) + (E_(x)^(2))/(E^(2)) - sqrt(2) (E_(y)E_(x))/(E^(2)) = (1)/(2)` This is clearly an ellipse. By comparing with the pervious CASE (compare the phase of `E_(y)` in the two cases ) we see this represents elliptical clockwise polarization when viewed towards the incoming wave. We write the equations as `E_(x) + E_(y) = 2Ecos(omegat - kz+(pi)/(8)) cos((pi)/(8))` `E_(x) - E_(y) = +2E sin (omegat - kz + (pi)/(8)) sin ((pi)/(8))` Thus `((E_(x) - E_(y))/(2Ecos((pi)/(8))))^(2) + ((E_(x) - E_(y))/(2esin((pi)/(8))))^(2) = 1` Since `cos((pi)/(8)) gt sin((pi)/(8))`, the major axis is the direction of the stright line `y = x`. (C) `E_(x) = Ecos (omegat - kz)` `E_(y) = Ecos(omegat - kz + pi) =- E cos (omegat - kz)` Thus the top of the electric vector traces the curve `E_(y) =- E_(x)` which is a stright line `~(y =- x)`. It corresponds to plane polarization. |
|
| 3022. |
A hollow charged sphere does not produce an electric field at any: |
|
Answer» POINT BEYOND 2 meters |
|
| 3023. |
Two mutually perpendicular conductors carry currents i_1 and i_2, along X-axis and y-axis respectively. The locus of the points at which magnetic induction is zero. |
|
Answer» `X= (i_1)/(i_2) y` |
|
| 3025. |
A : Light coming from numbers of calculator.s L.C.d display is polarised. R : The reflected light cannot be polarized when light is incident normal to the plane surface. |
|
Answer» Both A and R are true and R is the correct explanation of A |
|
| 3026. |
A thin magnetic needle oscillates in the horizontal plane with a time period of 2.0 s. If the needle is broken into 4 equal parts perpendicular to its length, then the time period of each part will be : |
|
Answer» 0.5 s |
|
| 3027. |
This story is about? |
|
Answer» Violence |
|
| 3028. |
A dipole consisting of an electron and a proton separated by a distance of 4 xx 10^(-10)m is situated in an electric field of intensity 3 xx 10^(5) NC^(-1) at an angle of 30^(@) with the field. Calculate dipole and torque acting on it. (e=1.6 xx 10^(-19)C). |
|
Answer» Solution :Data SUPPLIED, Charge of an ELECTRON `=|q_(1)|=e=1.6 xx 10^(-19)C` Charge on proton `=|q_(2)| =e =1.6 xx 10^(-19)C` Dipole length `=2a=4 xx 10^(-10)m` Dipole moment `p=2a xx " any of the charge "=4 xx 10^(-10) xx 1.6 xx 10^(-19)=6.4 xx 10^(-29) C.m.` Electric field intensity `E=3 xx 10^(5) NC^(-1), theta=30^(@), sin theta=sin 30^(@)=1/2` Torque,` tau =p E sin theta=6.4 xx 10^(-29) xx 3 xx 10^(5) xx 1/2=9.6 xx 10^(-23)Nm` |
|
| 3029. |
The capacitors in are initially uncharged and are cannected as in the diagram with switch S open. The applied potential differnce is V_(ab)= +360 V. . a. What is the potential differnce V_(cd) b What is the potential deffernce across each capacitor afrer switch S is closed? c. How much charge will flow through the awitch after it is closed? |
Answer»  `V_(a)V_(d)=6/(6+3)xx360=240 V` and `V_(a)-V_(c)=3/(6+3)xx360=120 V` (b) Refer to 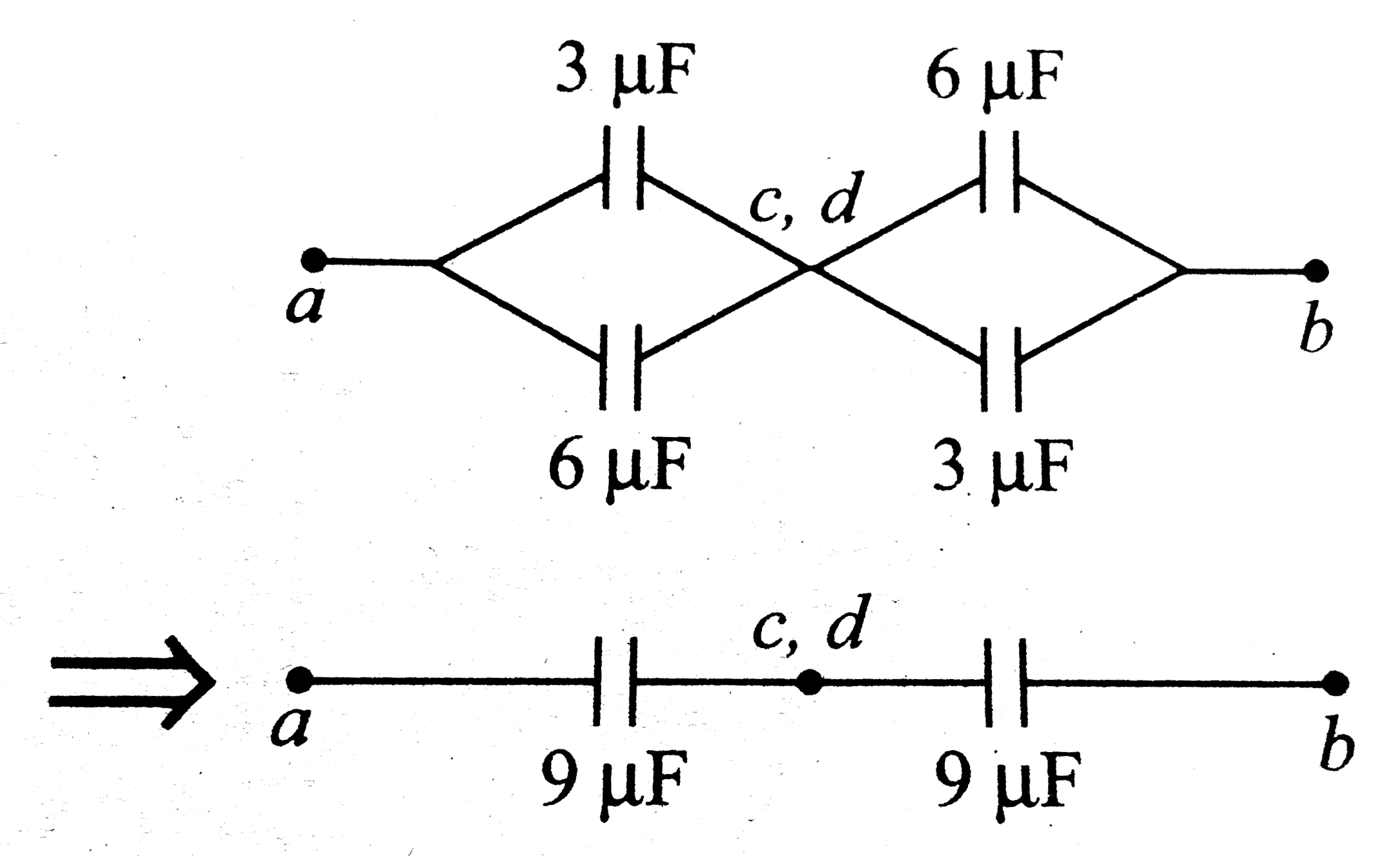 . . `V_(a)-V_(c)=V_(a)-V_(d)=V_(d)-V_(b)=V_(c)-V_(b)` `=(360)/2=180 V` That is, POTENTIAL across each capacitor is `180 V` c. Charge flowing after the SWITCH is closed: `Deltaq_(1)=1080-720=360 muC` `Deltaq_(2)=720-540=180 muC` Now, `Deltaq=Deltaq_(1) + Deltaq_(2) = 360 + 180 = 540 mu C` Hence, charge of `540 muC` flows from `c` and `d ` after closing the switch. 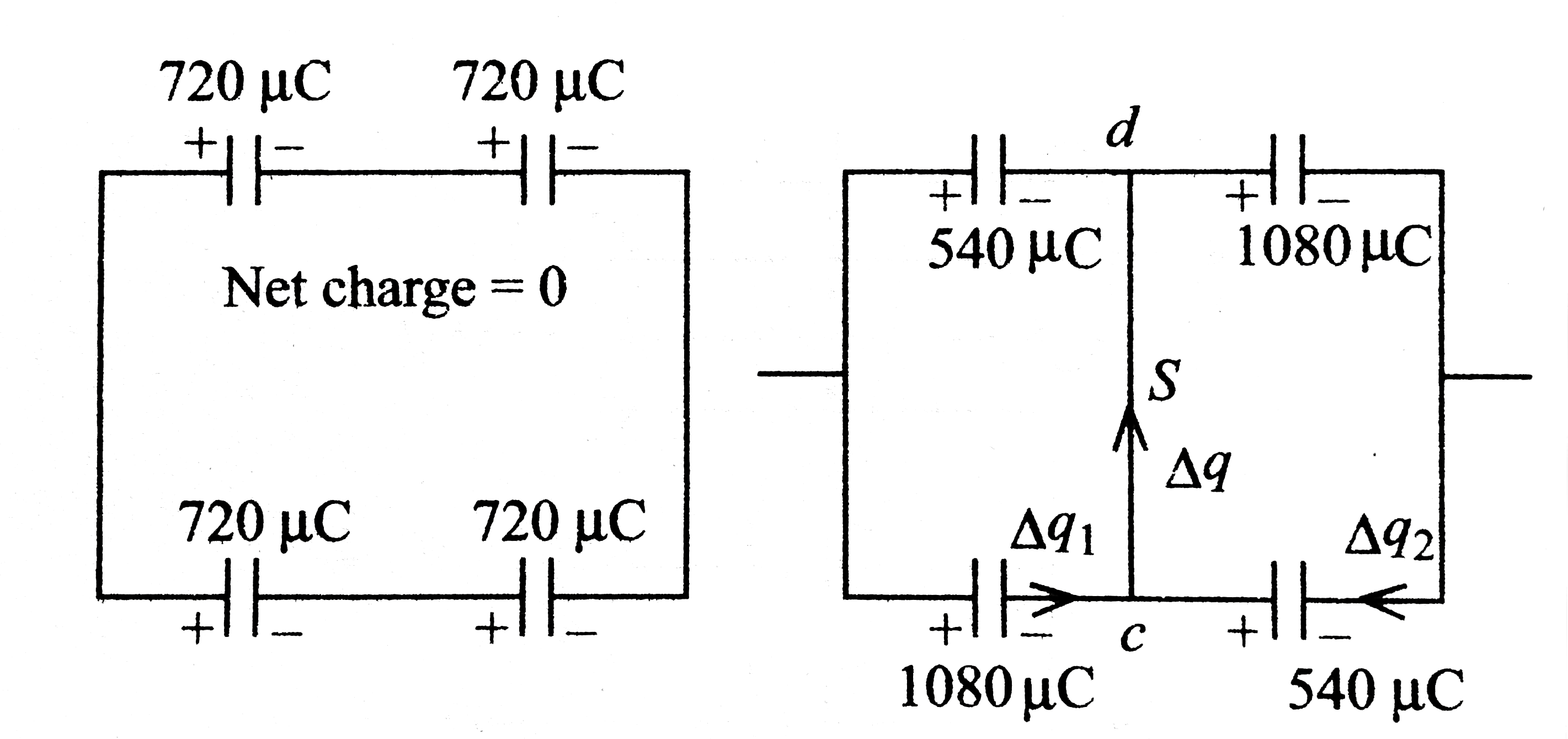 . .
|
|
| 3030. |
(a) Define the term activity of a sample of radioactive nucleus. Write its SI unit. (b) The half-life of " "_(92)^(238)U undergoing alpha-decay is 4.5 xx 10^(9) years. Determine the activity of 10 g sample of " "_(92)^(238)U. Given that 1 g of " "_(92)^(238)U contains 25.3 xx 10^(20) atoms. |
|
Answer» Solution : (b) Here `T_(1/2)=4.5 xx 10^(9) years = (4.5 xx 10^(9)) xx (3.154 xx 10^(7)) s`, mass of `" "_(92)^(238)U` (m) = 10 G and number of ATOMS per gram `= 25.3 xx 10^(20)`. `therefore` Total number of atoms in given sample `N = 10 xx 25.3 xx 10^(20) = 2.5 xx 10^(22)` `therefore` Activity `R= (-(DN)/(dt))=lambdaN=0.693/T_(1/2)=(0.693xx(2.53xx10^(22)))/(4.5xx10^(9)xx3.154xx10^(7))=1.235xx5s^(-1)=1.235xx10^(5)Bq` |
|
| 3031. |
What type of wave front will emerge from a poin source ? |
| Answer» Solution :Spherical wave front | |
| 3032. |
Calculate the wavelength associated with electrons whose speed is 2% of the speed of light. |
|
Answer» Solution :Data SUPPLIED, `v=3xx10^(8) xx (2)/(100)=6xx10^(6)ms^(-1), m=9.1xx10^(-31)KG, H = 6.625xx10^(-34)Js` `lambda=(h)/(mv)=(6.625xx10^(-34))/(9.1xx10^(-31)xx6xx10^(6))=1.213A^(@)` |
|
| 3033. |
If the focal length of objective lens is increased then magnifying power of ...... |
|
Answer» microscope will INCREASE but that of telescope decrease. `:.` As `f_(0)` INCREASES, magnifying power decrease hile magnifying power of telescope `=(f_(0))/(f_(e))` `:.` As `f_(0)` ncrease, magnifying power increases. |
|
| 3034. |
A light ray is incident perpendicular to one face of a 90^@ prism and is totally internally reflected at the glass-air interface. If the angle of reflection is 45^@, we conculde that for the refractive index n as |
|
Answer» `nlt (1)/(root_2)` i = C where i = incidence angle, C = CRITICAL angle `therefore sini gt sinC` `therefore sini gt 1/N` [`becausen=(1)/(sinC)]` `thereforen gt (1)/(sini)` `therefore n gt (1)/(sin45^@)""[becausei=45^@]` `therefore n gt sqrt2""[becausesin45^@=(1)/(sqrt2)` |
|
| 3035. |
What will be the self-inductance of a coil of 100 turns if a current of 5 amperes produces a magnetic flux of 5xx10^5Wb? |
|
Answer» 1mH |
|
| 3036. |
Relative permeability of a substance is 0.075. Its magnetic susceptibility is ........ |
|
Answer» `0.925` `mu_(r) = 1 + chi_(m)` but `mu_(r) = K_(m)` `therefore K_(m) = 1+ chi_(m)` `therefore chi_(m) = K_(m) - 1 = 0.075 -1 ` `therefore chi_(m) = -0.925` |
|
| 3037. |
Assertion : At neutral point, a compass needle may point out in any arbitrary direction. Reason : Magnetic field of the earth is balanced by field due to magnet at any neutral point. |
|
Answer» both are true and the Reason is the CORRECT EXPLANATION of the Assertion. |
|
| 3038. |
अनंत लंबाई वाले आवेशित बेलनाकार चालक के अक्ष से r दूरी पर विद्युत-क्षेत्र होगा |
|
Answer» `LAMBDA/(PI epsilon_0 r)` |
|
| 3039. |
What is the work done by magnetic force during this motion? |
| Answer» SOLUTION :ZERO (as DISPLACEMENT is PERPENDICULAR to FORCE) | |
| 3040. |
The statement (p to q) ∨ (q to p) is |
|
Answer» TAUTOLOGY 
|
|
| 3041. |
A cylindrical vessel of height 50 cm is filled with water and rests on a table. A small hole is made at the height h from the bottom of the vessel so that the water jet could hit the table surface at a maximum distance x_(max) from the vessel as shown in the figure. The value of x_(max)will be (Neglect the viscosity of water.) |
|
Answer» 15 cm  The given situation is shown in the figure. Range (MAXIMUM distance) is given by ` x = 2 SQRT(h (H - h) )`....(i) x will be maximum only when ` (dx)/(dh) = 0` `2.1 [h(-I) + (H - h)I] = 0` ` 2 sqrt(h (H - h) ) - h + (H - h ) = 0` ` H - 2h = 0` ` therefore h = (II)/(2)` Hence , x will be maximum, when ` h = H/2` ` therefore ` From Eqs. (i) we get ` x_(max) = 2 sqrt( H/2 ( H -H/2) )` ` = 2 sqrt( H/2. H/2) = H` ` x_(max) = 50 cm ` |
|
| 3042. |
A uniformly charged sphere hasa total charge of 300muC and radius of 8 cm. find the electric field (i) at a point 16 cm from the centre of the sphere (ii) at a point on the surface of the sphere (iii) at a point inside the sphere. |
|
Answer» |
|
| 3043. |
A ball weighing 10 gm hits a hard surface vertically with a speed of 5 m//s and rebounds with the same speed. The ball remains in contact with the surface for 0.01 sec. The average force exerted by the surface on the ball is : |
|
Answer» 0.1 N |
|
| 3044. |
For the situation show in the figure ("assume r" gt gt "length of dipole"). Select the correct statement(s) [vec(P) = dipole moment , Q = charge on the particle which is on equatorial line of dipole] |
|
Answer» FORCE acting on the DIPOLE is zero |
|
| 3045. |
In Frame 1, two identical conducting spheres, A and B, carry equal amounts of excess charge that have the same sign. The spheres are separated by a distance d, and sphere A exerts an electrostatic force on sphere B that has a magnitude F. A third sphere, C, Which is handled only by an insulating rod, is introduced in Frame 2. Sphere C is identical to A and B except that it initially uncharged. Sphere C is touched first to sphere A, in Frame 2, and then to sphere B, in Frame 3, and is finally removed in Frame 4. Determine the magnitude of the electrostatic force that sphere A exerts on sphere B in Frame 4. |
|
Answer» `(F)/(2)` |
|
| 3046. |
The angle of the prism is 60^@. What is the angle of incidence for minimum deviation? |
|
Answer» `45^@` |
|
| 3047. |
In the above problem, find the current through the cell at any time t. |
|
Answer» `(V)/(9R)+(V)/(R )E^((-t)/(CR))` |
|
| 3048. |
The current through a circular coil appears to be flowing in clock-wise direction for an observer. The magnetic induction at the centre of the coil is: |
|
Answer» perpendicular to the plane of the COIL and TOWARDS the observer |
|
| 3049. |
A : The soap film in sun light is colourful. R : Thin films produce interference of light. |
|
Answer» Both A and R are TRUE and R is the CORRECT EXPLANATION of A |
|
| 3050. |
Answer the following questions : (c ) Optical and radiotelescopes are built on the ground but X-ray astronomy is possible only from satellites orbiting the earth. Why? |
| Answer» Solution :In optical and radio-telescopes we use visible light and radiowaves, respectively, which can pass through atmosphere. Hence, such telescopes are built on the ground. However, X-rays haveextremely SMALL WAVELENGTHS and are absorbed by the atmosphere. Hence, X-ray astronomy is not possible from ground stations. X-ray astronomy is possible only from satellites ORBITING the earth at a height of 500 km or more. | |



