Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

36901.

State Gauss theorem in electrostatics. Prove that no electric field exists inside a hollow charged sphere.

Answer»

Solution :For Gauss theorem , refer under the heading " Chapter At A GLANCE "Consider a hollow CHARGED conducting sphere of radius R and having charge Q .To find electric field at a point P inside the shell , consider a sphere through point P and having centre O, i.E. r= The electric flux through the Gaussian surface
` ""phi _in = oint oversetto E . hat n ds = E 4 pi r^(2) `
According to Gauss theorem, TOTAL electric flux should be
` ""phi _in =(1)/( in _0)` (charged enclosed )= 0
[Since the Gaussian surface is not enclosing any charge]
Thus ` ""phi_in = E. 4 pi r^(2)=0"" ...(II) `
[Since the Gaussian surface is not enclosing any charge]
Thus ` phi _in =E. 4 pi r^(2) =0 `
`rArr ""E=0 `
Hence , no electric field exists inside a hollow charged sphere.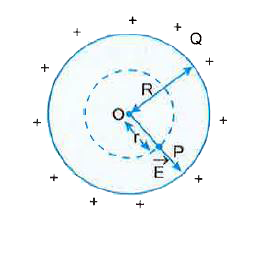
Discussion
36902.

(A ): The tails of comets are always oriented in a direction away from Sun (R) : Electromagentic waves exert pressure.

Answer»

Both 'A' and 'R' are TRUE and 'R' is the CORRECT EXPLANATION of 'A'.
Both 'A' and ’R' are true and 'R' is not the correct explanation of 'A
A' is true and 'R' is FALSE
'A' is false and R' is true

Answer :A
Discussion
36903.

What are electromagnetic waves ?

Answer»

SOLUTION :ELECTROMAGNETIC waves are coupled time-varying electric and MAGNETIC fields propagating in SPACE with the speed of light.
Discussion
36904.

The specific resistance of the material of a wire is 'rho' and its volume is 3m^3 and its resistance is 3 Omega . The length of the wire will be

Answer»

`(1)/(( sqrt(RHO))`
`(3)/( sqrt((rho ))`
`( sqrt(3))/(rho)`
`(rho)/( sqrt(3))`

ANSWER :B
Discussion
36905.

A resistance of 300 Omega and inductance of 1//pi henry are connected in series to an alternating voltage of 20 V and 200 Hz frequency. The phase angle between the voltage and current is

Answer»

`tan^(-1)((3)/(4))`
`tan^(-1)((3)/(2))`
`tan^(-1)((4)/(3))`
`tan^(-1)((2)/(3))`

Solution :Phase angle `= phi`
`THEREFORE tan phi = (L omega)/(R )=(2pi fL)/(R )=(2pi xx 200)/(300 xx pi)=(4)/(3) rArr phi = tan^(-1)((4)/(3))`
Discussion
36906.

Light of wavelength lambda is incident on slit of width d. The resulting diffraction pattern is observed on a screen placed at distance D. The linear width of central maximum is equal to width of the slit then D = .......

Answer»

`(d^(2))/(2lambda)`
`(d)/(lambda)`
`(2lambda^(2))/(d)`
`(2lambda)/(d)`

Solution :For first ORDER diffraction,
`d SIN theta= lambda`
For small angle,
`d (theta)=lambda`
For first order diffraction on both side of Q,
`d(2 theta)=2lambda`
but `theta=(X)/(D)`
`:.d((2X)/(D))=2lambda`
`:.(d(d))/(D)=2lambda( :.2x=d` given )
`:.(d^(2))/(D)=2 lambda`
`:.D=(d^(2))/(2lambda)`
Discussion
36907.

Total electric fulx coming out of a unit positive charge put in air is

Answer»

`epsilon_(0)`
`epsilon_(0)^(-1)`
`(4 PI epsilon_(0))^(-1)`
`4 pi epsilon_(0)`

ANSWER :A
Discussion
36908.

If nij is reftactive index of medium i with respect to medium j n_21 X n_32 X n_43 = ..........

Answer»

`3^(MU)""_1`
`3^(mu)""_2`
`(1)/(1^(mu)""_4)`
`4^(mu)""_2`

Solution :`""_2mu_1xx""_3mu_2xx""_4mu_3=(mu_1)/(mu_2)XX(mu_2)/(mu_3)xx(mu_3)/(mu_4)`
`=(mu_1)/(mu_4)=""_4mu_1=(1)/(""_1mu_4)`
Discussion
36909.

Calculate the maximum possibleenergy of the gamma rays emitted by an excited ""^(11)B nuclues formed by the capture of a slow neutron by a ""^(10)B nucleus. Take mass of ""^(10)B=10.012938u and ""^(11)B=11.009305u

Answer»


ANSWER :11.44MeV
Discussion
36910.

The volume of the piece of glass Is

Answer»

`166cm^3`
`60 cm^3`
`1.6 cm^3`
`1666 cm^3`

SOLUTION :The volume of the glass MAY be calculated as FOLLOWS :
10.000 gm x `(1 cm^3)/"6 gm"= 1666 cm^3`
Discussion
36911.

Michael faradey observed that whenever magnetic flux linked with a coil changes ,an emf is induced in the coil.suppose a coil of N turns and Radius R is kept normal to a varrying magnetic field B=B_0 cos Omega t. Obtain the emf induced in the coil.

Answer»

SOLUTION :INDUCED EMF `epsilon`=`(-dphi//dt)`=-`d[NB_0(pi R^2)cos OMEGA t//dt]`=-NB_0(piR^2)(-SIN omega t,omega)`=` `NB_0(pi R^2) omega sin omega t``
Discussion
36912.

Define the quality factor in an a.c, resonant circuit. Why should the quality factor have high value in receiving circuits ? Name the factors on which it depends.

Answer»

Solution :For .Quality FACTOR., see Point Number 19 under the HEADING "Chapter At A Glance." If the resonance is less sharp, the CIRCUIT is close to resonance for a LARGER range of Aw of frequencies and the tuning of the circuit will not be good i.e., the selectivity of the circuit will be poor. Due to this reason we want a high value of quality factor in receiving sets (RADIO sets) so that the radio receiver has a high value of selectivity
Discussion
36913.

Michael faradey observed that whenever magnetic flux linked with a coil changes ,an emf is induced in the coil. Suppose a coil of N turns and Radius R is kept normal to a varrying magnetic field B=B_0 cos Omega t What is the flux linked with coil at any instant t?

Answer»

SOLUTION :`phi=BAN=B_0cosomegatAN=NB_0Acosomegat` Here `A=pir^2` `THEREFORE` `phi=NB_0(PI R^2) COS OMEGA t`
Discussion
36914.

A flat disc of radius 'R' lie son the horizontal surface. The pressure between the disc and the surface decreases linearly with distance from the centre r due to its weight per unit area from 2P_(0) at th ecentre to P_(0) at r = R at the circumference. The coefficient of friction between the disc and the surface is 'mu'. Find the power delivered by the external agent to rotate the disc with a constant angular velocity omega

Answer»

`( 5)/( 6) pi P_(0) R^(3) omega MU`
`( 7)/( 6) pi P_(0 ) R^(3) omega mu`
`(3)/( 6) pi P_(0) R^(3) omega mu`
`(11)/( 6) pi P_(0)R^(3) omega mu`

Answer :A
Discussion
36915.

How much emf is induced in a coil of self-inductance 2H if the current in it.is changing at the rate of 2 As^(-1) ?

Answer»

SOLUTION :`L = 2H, (DI)/(dt) = 2As^(-1)`
We have `EPSI = L (dI)/(dt)`
`epsi = 2 xx 2 `
` epsi = 4V`
Discussion
36916.

Change on two particle is 3q and 2q respectivley.Their mass is 2m and 3m respectively.Both are accelerated under same potential difference .Ratio of their de-Broglie wavelength will be….

Answer»

`2:3`
`3:2`
`1:`
`1:1`

SOLUTION :In `lambda=(h)/(sqrt(2mVq))`,h,2 and V are same.
`THEREFORE lambda prop (1)/(sqrt(mq))`
`therefore (lambda_(1))/(lambda_(2))=sqrt((m_(2)q_(2))/(m_(1)q_(1)))=sqrt((3m)/(2M)xx(2q)/(3q))=sqrt(1)`
`therefore (lambda_(1))/(lambda_(2))=1:1`
Discussion
36917.

A cell supplies a current of 0.9 A through a 1 Omega resistor and a current of 0.3 A through a 2Omega resistor. Calculate the internal resistance of the cell.

Answer»

Solution :Current from the CELL, `I_(1)=0.9A`
Resistor, `R_(1)=2OMEGA`
Current from the cell, `I_(2)=0.3A`
Resistor, `R_(2)=7Omega`
Internal resistance of the cell, `r=?`
Current in the circuit, `I_(1)=(XI)/(r+R_(1))`
`xi=I_(1)(r+R_(1)) ""...(1)`
Current in the circuit, `I_(2)=(xi)/(r+R_(2))`
`xi=I_(2)(r+R_(2))""...(2)`
Equating equation (1) and (2),
`I_(1)r+I_(1)R_(1)=I_(2)R_(2)+I_(2)r`
`(I_(1)-I_(2))r=I_(2)R_(2)-I_(1)R_(1)`
`r=(I_(2)R_(2)-I_(1)R_(1))/(I_(1)-I_(2))=((0.3xx7)-(0.9xx2))/(0.9-0.3)=(2.1-1.8)/(0.6)=(0.3)/(0.6)`
`r=0.5Omega`
Discussion
36918.

Calculate the deflection of the beam of atoms from its axis in the Stern-Gerlach experiment for the following parameters of the apparatus: the length of pole pieces is 3.5 cm. the magnetic field gradient is of the order of 10^2 T//m. In the experiment silver atoms flying out of a "molecular oven" at a temperature of 730^@C were deflected. The projection of the magnetic moment of a silver atom on the direction of the magnetic induction vector is equal to a Bohr magneton.

Answer»


Solution :The FORCE acting on an atom whose magnetic moment is `p_(m)=PM mu_(B)" is "F=p_(m) (dB)/(dx)," where "(dB)/(DZ)` is the magnetic field gradient. The deflection is `H=at^2//2` where a=F/m, t=l/v. SUBSTITUTING, we obtain `h=(p_(m)l^2)/(2mv^2) (d B)/(dz)`
But `1//2 mv^2=3//2kT,` Therefore the final result is
`h=pm (mu_(B)l^2)/(6kT) (dB)/(dz)`
Discussion
36919.

If identical charges (-q) are placed at each corner of a cube of side b, then electric potential energy of charge (+q) which is placed at centre of the cube will be

Answer»

`(8 sqrt (2)q^2)/(4 piepsi_0 B)`
`(-8 sqrt( 2)q^2 )/(PI epsi_0 b)`
`(-4 sqrt( 2) q^2 )/( pi epis_0 b)`
`(-4 q^2)/( sqrt(3 )piepsi_0 b)`

ANSWER :D
Discussion
36920.

At a given instant, there are 25% undecayed radioactive nuclei in a sample. After 10 seconds the number of undecayed nuclei reduces to 12.5%, the mean life of the nuclei is

Answer»


ANSWER :14.43
Discussion
36921.

Stae two conditions to obtain sustained interference of light ?

Answer»

SOLUTION :The conditions for obtaining SUSTAINED interference of light are
(i) The two light SOURCES MUST be COHERENT.
The two light sources should be narrow and placed close to each other.
Discussion
36922.

At 45^(@)to the magnetic meridian theapparentis 60^(@) the true dip is

Answer»

`TAN^(-1)SQRT(3)`
`tan^(-1)""(1)/(sqrt(3))`
`tan^(-1)sqrt(3/2)`
`tan^(-1)sqrt(1/6)`

SOLUTION :APPARENT dip `delta` is given by
`tan delta=(v)/(H)=(V)/(H cos 45^(@))=(V)/(H)xx(1)/(cos 45^(@))`
but `tan 60^(@) =tan delta sqrt(2)`
`tan delta =sqrt(3)//2therefore delta =tan^(-1) sqrt(3)//2`
or `tan delta =sqrt(3)//2 therefore delta =tan^(-1) sqrt(3)//2`
`rarr tan delta =tan delta cos alpha=sqrt(3)/(2)`
Discussion
36923.

If a ray of light is incident at a glass surface at the Brewster's angle of 60^(@), then the angle of deviation inside glass is

Answer»

a. `90^(@)`
B. `60^(@)`
c. `45^(@)`
d. `30^(@)`

Answer :D
Discussion
36924.

How will the frequency of small oscillation of a simple pendulum changes. If it moves vertically down with acceleration a lt g or with acceleration a gt g

Answer»

SOLUTION :DECREASES, No oscillation if a = G, frequency may increase or decrease depending on MAGNITUDE of a
Discussion
36925.

Two electric bulbs rated 50 W and 100 W are glowing at full powr, when used in parallel with a battery of emf 120 V and internal resistance10 Omega. The maximum number of bulbs that can be connected in the circuit when glowing at full power, is

Answer»

6
4
2
8

Answer :B
Discussion
36926.

In the rectangle, shown below, the twp corners have charges q_(1)=-5muC and q_(2)=+ 2.0 muC. The work done in moving a charge +3.0 muC from B to A is (take 1//4 pi epsilon_(0)=10^(10)"N-m"^(2)//C^(2))

Answer»

2.8 J
3.5 J
4.5 J
5.5 J

Answer :A
Discussion
36927.

How is radius of nucleus related to mass number ?

Answer»



SOLUTION :`R=R_(0)A^(1//3)`.
Discussion
36928.

The graph shows photoelectric current with anode potential.The potential at .O. is called

Answer»

A) ACCELERATING POTENTIAL
B) RETARDING potential
C) STOPPING potential
D)SATURATION potential

Solution :Stopping potential
Discussion
36929.

What is the direction of diffusion current in a junction diode?

Answer»

Solution :The DIRECTION of DIFFUSION current is from P to N in a semiconductor JUNCTION diode.
Discussion
36930.

Number of possible point C such that area of triangleABC is 10 square unit where A(0,6),B(8,0) and angleACB=90^@ , is

Answer»

0
2
4
Infinite

Solution :`angleACB=90^@`
So, A,C,B lie on the circle WHOSE DIAMETERIS 10

Maximum area of `DeltaABC` is `=1/2xx5xx5=25/2`
Required area is 10
Discussion
36931.

A cirular loop of radius 1m is kept in a magnetic field of strength 2T (plane of loop is perpendicular to direction of magnetic field). Resistance of the loop wire is (2)/(pi) Omega//m. A conductor of legth 2m in sliding with a speed 1ms as shown in figure. Find the instantaneous force acting on the road (assume rod has negligible resistance).

Answer»

8N
16N
32N
64N

Answer :B
Discussion
36932.

At a certain place, the horizontal component of earth's magnetic field is sqrt3 times the vertical component.The angle of dip at that place is

Answer»

`30^(@)`
`60^(@)`
`45^(@)`
`90^(@)`

SOLUTION :`"since" V = H TAN THETA and H = sqrt3V`
`therefore V = sqrt3V tan theta`
`therefore tan theta =1/sqrt3 = tan 30^(@) IMPLIES theta 30^(@)`
Discussion
36933.

When eddy currents are produced in the conductor, electrons in that conductor _____

Answer»

do not MOVE
move on the paths of MINIMUM resistance (KNOWN as EDDIES)
move on the paths of MAXIMUM resistance
move on random paths

Answer :B
Discussion
36934.

In the given circuit , when key K is open, reading of ammeter is I. Now key K is closed, then the correct statement is

Answer»

If `epsilon_1 lt IR`, reading OG the ammeter is less than I.
If `IR GT epsilon_1`, reading of the ammeter is greater than I.
If `epsilon_1gt 2IR`, reading og the ammeter will be ZERO.
Reading of ammeter will not CHANGE.

Solution :b. `R(i_1 + i_2) = E_1`
`i_2R + (i_1 + i_2) R = E_2`
`i_2 = (E_2 - E_1)/R `
[Initially, `E = E_2//R`].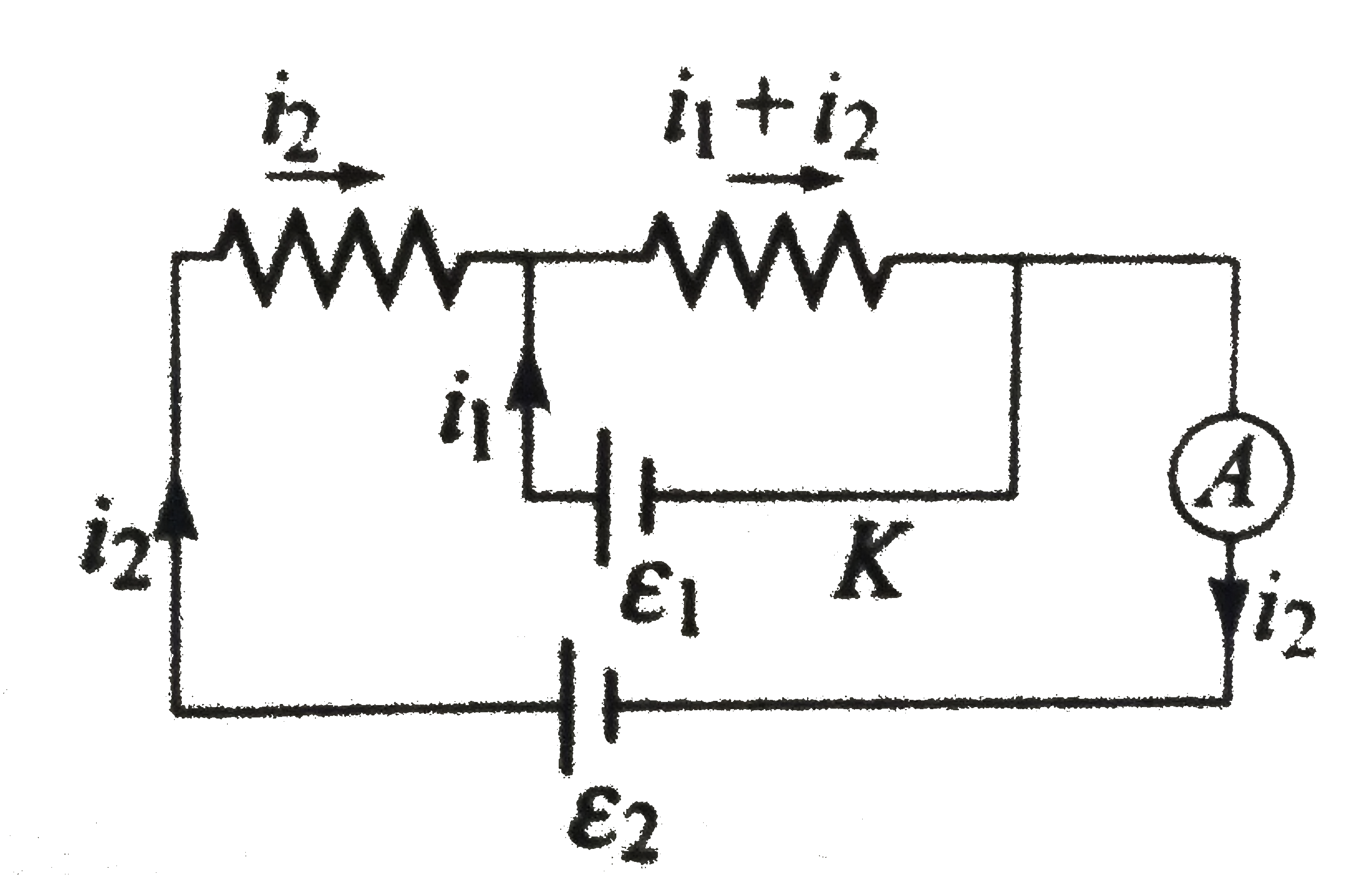
Discussion
36935.

Simplify Y = AB+ABC +barAB+ AbarBC using Boolean Algebra. Draw the resultant simplified logic circuit.

Answer»

SOLUTION :GIVEN `Y=AB+ABC+barAB+AbarBC`
`Y=(A+barA)B+AC(B+barB)=B+AC (because B+barB=1)`
LOGIC CIRCUIT is SHOWN below.
Discussion
36936.

The distance of the closest approach of an alpha particle fired at a nucleus with momentum P is r_0. The distance of the closest approach when the alpha particle is fired at the same nucleus with momentum 2P will be

Answer»

`2r_0`
`4r_0`
`r_0/2`
`r_0/4`

ANSWER :D
Discussion
36937.

The dimensional formula for hole mobility in a semiconductor is :

Answer»

`[M^(-1)L^(0)T^(2)A]`
`[M^(-1)L^(2)T^(-2)A]`
`[M^(0)L^(0)T^(0)A]`
`[ML^(-2)T^(-2)A]`

Solution :`[mu_(H)]=("drift VELOCITYV")/("electric field E")=([LT^(-1)][AT])/([MLT^(-2)])=[M^(-1)T^(2)A].`
Hence `(a)` is the correct choice.
Discussion
36938.

A boat which has a speed of 5 km h^(-1) in still water crosses a river of width 1 km along the shortest possible path in 15 minutes. The velocity of the river water in km h^(-1) is

Answer»

1
3
4
`sqrt41`

Solution :Resultant velocity of boat, `v="1 KM"/"15 MIN"`
`="1 km"/"(1/4) h"=4"km h"^(-1)`
Velocity of RIVER, `v_R=sqrt(v_B^2-v^2)=sqrt(5^2-4^2)=3 "km h"^(-1)`
Discussion
36939.

When a current I is established in a coil of self-inductance L, energy stored in the inductor is ______.

Answer»


ANSWER :`1/2LI^(2)`
Discussion
36940.

Following figure shows the multiple reflections of a light ray along a glass corridor where the walls are either parallel or perpendicular to one another. If the angle of incidence at point P is 30^(@), what are the angles of reflection of the light ray at points Q , R , S and T respectively

Answer»

`30^(@), 30^(@), 30^(@), 30^(@)`
`30^(@), 60^(@), 30^(@), 60^(@)`
`30^(@), 60^(@), 60^(@), 30^(@)`
`60^(@), 60^(@), 60^(@), 60^(@)`

ANSWER :C
Discussion
36941.

The arrangement shown in figure performs the logic function of

Answer»

AND GATE
NAND gate
OR gate
XOR gate

Answer :A
Discussion
36942.

A cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is p. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and centre of cavity are separated by a distance a. The time after which the electron again touches the sphere is

Answer»

`sqrt((6sqrt(2)repsilon_(0)m)/(epa))`
`sqrt((sqrt(2)repsilon_(0)m)/(epa))`
`sqrt((6repsilon_(0)m)/(epa))`
`sqrt((repsilon_(0)m)/(epa))`

Solution :TORQUE due to `vec(B)` = Torque of weight of (QRST) (about QT)
`L(B_(0)IL)=3(lambdaL)g((L)/(2)+(L)/(6))=3lambdaLg((2L)/(3))`
`B_(0)=(2lambdag)/(I)`
No EXTERNAL force, so COM cannot displace initial coordinate of `COM=(3(lambdaL)("zero")+2lambdaL((L)/2)+lambdaL(L))/(6lambdag)=(L)/(3)`
Final coordinate of `COM=(L)/(3)("same")`
But COM DISPLACES with respect to QT by `(2L)/(3)`. So displacement of `QPUT=(2L)/(3)`.
Initial magnetic dipole moment M makes an angle of `(pi)/(4)` ACW from +ive x-axis and finally it makes angle `(3pi)/(4)` ACW from `+"ive x-axis" (M=sqrt(2)IL^(2))`
So change in `PE=-MB(cos theta_(2)-costheta_(1))=MB_(0)[cos135^(@)-cos45^(@)]=2B_(0)IL^(2)="Gain in KE"=(1)/(2)I omega ^(2)`
`I("about QT")=2[(2lambdaL^(3))/(3)+lambdaL^(3)]=(10lambdaL^(3))/(3),2B_(0)IL^(2)=(1)/(2)(Iomega^(2))=(1)/(2)((10lambdaL^(3))/(3))omega^(2),omega^(2)=(6B_(0)I)/(5lambdaL)`
Discussion
36943.

Choose the correct alternative (s) from the following .

Answer»

The NUMBER of significant figures in 0.080 is 2.
The number of significant figure is `3.04 XX 10^(23)` is 25
The number of significant figures in 0.01020 is 4.
The number of significant figures in `4.06 xx 10 ^(-4)` is 3.

ANSWER :A::C::D
Discussion
36944.

Light incident normally on a plane mirror attached to a galvanometer coil retraces backwards as shown in Fig. 9.33. A current in the coil produces a deflection of 3.5^(@) of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?

Answer»

Solution :The reflected rays get deflected by TWICE the angle of rotation of the MIRROR. THEREFORE, `d//1.5 = tan 7^(@)`. Hence `d = 18.4 cm.`
Discussion
36945.

Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20cm?

Answer»

SOLUTION :R = 22CM
Discussion
36946.

A Tuning fork M of frequency 150 Hz given 10 beats in 2 sec with a tuning fork N. when M is lightly loaded 6 beats in 2 sec are heard. Frequency of N is

Answer»

155 Hz.
153 Hz.
145 Hz.
17 Hz.

Answer :A
Discussion
36947.

उत्तल लेंस में जब वस्तु (बिव) फोकस एवं लेंस के बीच रखी जाती है तब कैसा प्रतिबिंब बनता है ?

Answer»

काल्पनिक और सीधा
काल्पनिक और उलटा
वास्तविक और उलटा
वास्तविक और सीधा

Answer :A
Discussion
36948.

An artificial satellite is revolving round a planet of mass M and radius R in a circular orbit of radius 'r' . If its period of revolution T obeys Kepler's law i.e. T^(2)propr^(3). What is relation for the period of revolution in terms of R,r and "g" the accelerations due to gravity on the planet ?

Answer»

`T=kr^(3/2)R^(1/2)g^(1/2)`
`T=kr^(3)Rg^(1/2)`
`T=kr^(3/2)R^(-1)g^(1/2)`
`T=kr^(3/2)R^(2)g`

Solution :Here `T^(2)propr^(3)` ( Kepler.s law )
`:.Tpropr^(3//2)...(2)`
ALSO let `Tpropg^(a)R^(b)`
`:.Tpropr^(3//2)g^(a)R^(b)`
Putting the DIMENSIONS
`M^(0)L^(0)T^(1)=k[L]^(3//2)[L^(1)T^(-2)]^(a)[L^(1)]^(b)`
`=kL^(3//2+a+b)T^(-2a)`
Comparing the dimension
`3//2+a+b=0`
`3//2-(1)/(2)+b=0`
`:.b=-1`
`-2a=1`
`a=-(1)/(2)`
`:.T=kr^(3//2)g^(-1//2)R`
`=(k)/(R)sqrt((r^(3))/(g))`
HENCE `(C )` is correct.
Discussion
36949.

Two plano concave lenses of glass of refractive index 1.5 have radii of curvature 20 cm and 30 cm respectively. They are placed in contact with the curved surface towards each other and the space between them is filled with a liquid of refractive index 5/2. The focal length of the combination is (in cm)

Answer»

6
`-92`
`108`
12

Answer :D
Discussion
36950.

How volt and weber are related?

Answer»

SOLUTION :1 VOLT = weber/second.
Discussion