Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 41101. |
Illustrate by giving suitable examples, how you can show that electromagnetic waves carry both energy and momentum. |
| Answer» Solution :As an electromagnetic WAVE CONTAINS both ELECTRIC and MAGNETIC fields, it must carry energy and consequently MOMENTUM too. | |
| 41102. |
What happens to the length of a ferromagnetic rod when it is magnetised? |
| Answer» Solution :The LENGTH slightly INCREASES because of the ALIGNMENT of the DOMAINS in the DIRECTION of the external field. | |
| 41104. |
Using Ohm's law, calculate the resistance of combination of few resistances joined in series. |
Answer» Solution :Resistance in series. Resistances are SAID to be connected in series if they are joined end to end and the same (i.e. total) current flows through each one of them. Since there is a single path for moving CHARGE, the same current must flow through each resistor. 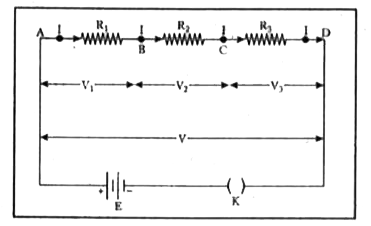 Let `R_(1),R_(2) and R_(3)`=three resistances connected in series. I=current flowing through `R_(1),R_(2) and R_(2)` V=potential difference across A and D `V_(1),V_(2) and V_(3)=`potential difference across `R_(1),R_(2) and R_(3)` RESPECTIVELY. It is clear from the circuit diagram that `V=V_(1)+V_(2)+V_(3)`. . . (1) According to Ohm.s law, `V_(1)=IR_(1),V_(2)=IR_(2) and V_(3)=IR_(3)`. . (2) let `R_(S)` be the resultant resistance. Obviously, when such a resistance is connected between A and D and a potential V is applied across its ends, it allows a current I through it. `therefore V=IR_(S)`. . (3) Substituting respective VALUES in eqn. (3) `IR_(S)=IR_(1)+IR_(2)+IR_(3)=I(R_(1)+R_(2)+R_(3))` or `R_(S)=R_(1)+R_(2)+R_(3)`. . (4) Hence when a NUMBER of resistances are connected in series, the total or resultant resistance is equal to the sum of the individual resistances. If there are n resistances and each is equal to R and if they are connected in series, then their resultant is given by `R_(S)=R+R+R+R`. . . n times. or `R_(S)=nR`. . . (5) i.e. `R_(S)`=number of resistances`xx` value of each resistance. Thus effective resistance increases. |
|
| 41105. |
The angle of minimum deviation for a 75^@ prison of dense glass is found to be 45^@ when in air and 15^@ when immersed in certain liquid. The refractive index of the liquid is, |
|
Answer» `(SQRT3)/(2)` |
|
| 41106. |
Ensure the distance for which ray optics is good approximation for an aperture of 4mm and wavelength 400 nm |
|
Answer» 0.01 m |
|
| 41107. |
How a human being can live happily? |
|
Answer» When his mind and HEART is open and violence free |
|
| 41108. |
The logic circuit shown belows has the input waveforms 'A' and 'B' as shown. Pick out the correct output waveform |
|
Answer»
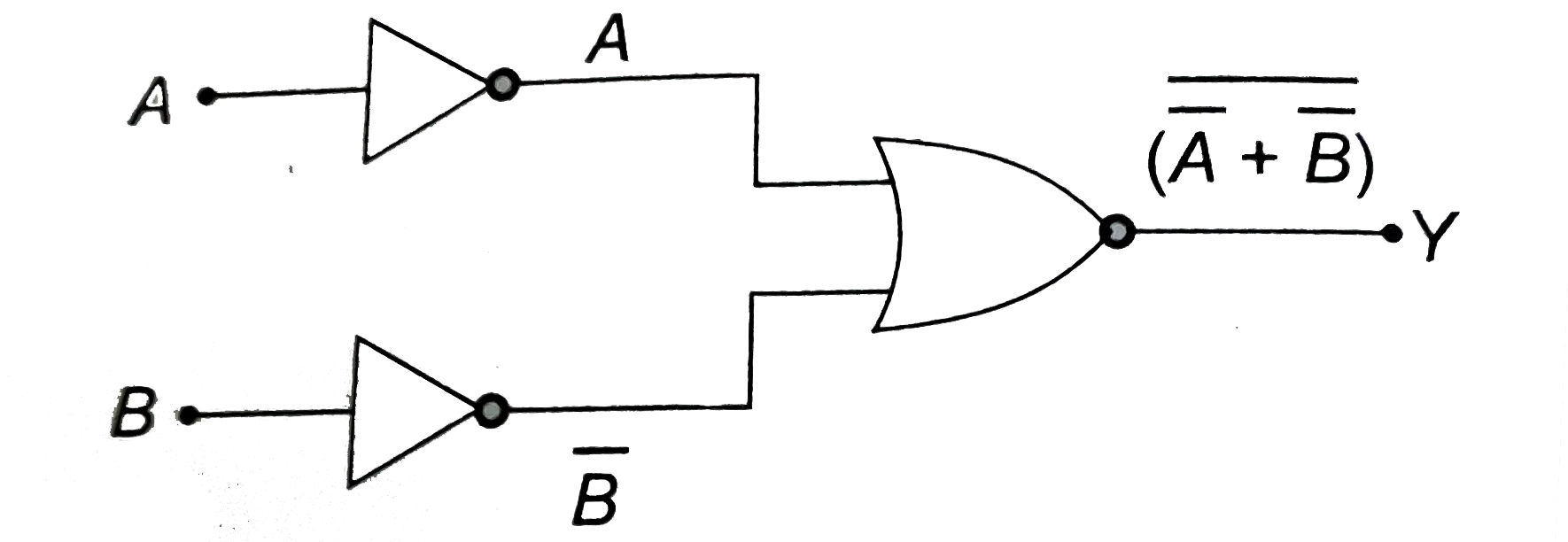
|
|
| 41109. |
A copper strip is introduced in the left gap and a resistance R-0.4 Omega is placed in the right gap of a meter bridge experiment. The balance points before and after interchanging the copper strip and the resistance R are 30 cm and 60 cm respectively. The resistance per unit length of the bridge wire is |
|
Answer» `4 OMEGA.m^(-1)` |
|
| 41110. |
Three resistance 2Omega, 3Omega and 5Omega are connected in series and a p.d. of 20V is applied across the terminals of combination. The p.d. across 5Omega resistance is |
|
Answer» 20 V |
|
| 41111. |
A small sphere of mass m and radius r is placed inside a horizontal hollow cylinder of radius R. Now cylinder rotating with some angular acceleration which slowly increases from zero to certain value alpha. |
|
Answer» Maximum angle `theta` formed by LINE joining centre will be `theta=sin^(-1)((2alphaR)/(5G))` `7/5 alphar-alphar=gsintheta` `theta=sin^(-1)((2alphar)/(5g))` |
|
| 41112. |
A dielectric slab fills the space between the plates of a parallel-plate capacitor. The magnitude of the bound charge on the slab is 75% of the magnitude of the free charge on the plates. The capacitance is 480muf and the maximum charge that can be stored on the capacitor is 240varepsilon_(0)L^(2) E_(max) where E_(max) is the breakdown field. |
|
Answer» the dielectric constant for the dielectric SLAB is 4 `(240in_(0)L^(2))/(kAin_(0)) A=60L^(2)` `(4in_(0)A)/d=480` `(in_(0)A)/(d-d/2(1-1/4))=120xx8/5=192` |
|
| 41113. |
A galvanometer of resistance 50 Omega is connected to a battery of 3 V along with a resistance of 2950 Omega in series shows full-scale deflection of 30 divisions. The additional series resistance required to reduce the deflection to 20 divisions is |
|
Answer» `1500 Omega` `I=(3)/((50+2950))` `I=10^(-3)A` Current for 30 DIVISION `= 10^(-3)A` Current for 20 division `= (10^(-3))/(30)xx20-(2)/(3)xx10^(-3)A` Let the SERIES resistance = R `therefore (2)/(3)xx 10^(-3)=(3)/((50+R))` `R = 4450 Omega` Option (c ) is nearest option in the given options. 
|
|
| 41114. |
Protons are acceleratedin a cyclotronso that the maximum curvatureradiusof theirtrajectoryis equalto r = 50 cm. Find: (a) the kinetic energyof the protonswhen the acceleration is completedif the magnetic induction in the cyclotron is B= 1.0 T, (b) the minimum frequencyof the cycloroton'soscillator at whichthe kinetic energyof theprotons amountsto T = 20 Me V by theend of accelearation. |
|
Answer» SOLUTION :(a) From `(mv^(2))/(R) = Bev`, or, `mv = BER` and`T = ((Ber)^(2))/(2m) = (1)/(2) mv^(2) = 12 MeV` (b) From `(2pi)/(omega) = (2pi r)/(v)` we get, `f_(min) = (v)/(2pi r) = (1)/(pi r) sqrt((T)/(2m)) = 15 MHz` |
|
| 41115. |
A circular coil of 10 turns and mean radius of 0.1 m is kept with its plane in the magnetic meridian. If a current of 2 A passes through it, calculate the resultant magnetic field at its centre. (B_(H)=4 times 10^(-5)T) |
|
Answer» Solution :Magnetic FIELD at the centre, `""=(mu_(0)/(4pi))((2pini)/(R))tesla` `""B_(C)=(10^(-7) times 2 times 3.142 times 10.2)/(0.1) tesla` `""=12.57 times 10^(-5)T.` `""B_(R)=sqrt(B_(H)^(2)+B_(C)^(2))` `""=10^(-5)sqrt((4)^(2)+(12.57)^(2))` `""=10^(-5)sqrt(174.0)` `""B_(R)=13.19 times 10^(-5)T` Resultant magnetic field `=13.2 times 10^(-5)T`. 
|
|
| 41116. |
Solar radiation is: |
|
Answer» TRANSVERSE ELECTROMAGNETIC wave |
|
| 41117. |
What should be the height of the plane mirror which will enable a person to see his full image ? |
| Answer» SOLUTION :The HEIGHT of the MIRROR should be HALF the height of the PERSON. | |
| 41118. |
200 Omega resistor is connected in one of the gaps of the meter bridge. Series combination of X Omega and 50 Omega resistors is connected in the second gap. Here unknown resistance X Omegais kept in a heat bath at a certain temperature. The unknown resistance and its temperature is....... and.......respectively if the balance point is obtained at 50 cm. The total length of the wire of the meter bridge is equal to 1 meter. The resistance of the unknown resistance at 0" "^(@)Ctemperature is equal to 100 Omega . alpha = 0.5 xx 10^(-3) ""^(@) C^(-1) for the material of the X Omega resistors. |
|
Answer» Solution :`R_(1)= 200 OMEGA, "" R_(2) = (X + 50) Omega` `l_(1) = 50 cm , "" l_(2) = 100 - 50 = 50 cm ` Here , we have`(R_(1))/(R_(2)) = (l_(1))/(l_(2))` `therefore (200)/(X + 50) = (50)/(50) ` `therefore X +50 = 200 ` `therefore X= 150Omega` Now, X = `X_(0) [ 1 + ALPHA (theta - 0 ) ] ` `therefore 150 = 100 [ 1 + 5 xx 10^(-3) theta ]` `therefore 1.5 = 1+ 5 xx 10^(-3) theta` `therefore theta = 100^(@) `C |
|
| 41119. |
A ball of mass 150g starts moving at 20 m/s^2 and hit by a force which acts on it for 0.1 second. Then the impulsive force is |
|
Answer» 75 N |
|
| 41120. |
S_(1) and S_(2) are two loudspeakers with the same frequency of 165 Hz and acoustic output 1.2 xx 10 ^(-3) and 1.8 xx 10^(-3) watts respectively/ They vibrate in the same phase. P is a point at a distance 4m from S_(1) and3m from S_(2) What is the intensity at P with S_(1) and S_(2) on? |
|
Answer» |
|
| 41121. |
S_(1) and S_(2) are two loudspeakers with the same frequency of 165 Hz and acoustic output 1.2 xx 10 ^(-3) and 1.8 xx 10^(-3) watts respectively/ They vibrate in the same phase. P is a point at a distance 4m from S_(1) and3m from S_(2) What is the intensity of sound at P if S_(2) is turned off? |
|
Answer» |
|
| 41122. |
Obtain the resonant frequency and Q-factor of a series LCR circuit with L = 3.0 H, C = 27 muF, and R = 7.4 Omega. It is desired to improve the sharpness of the resonance of the circuit by reducing its ‘full width at half maximum’ by a factor of 2. Suggest a suitable way. |
|
Answer» Solution :`omega_(0)=111 "rad s"^(-1), Q=45` To DOUBLE Q WITHOUT CHANGING `omega_(0)`, reduce R to 3.7 `OMEGA`. |
|
| 41123. |
In germanium crystal, a hole is provided by a ______ impurity. |
|
Answer» covalent |
|
| 41124. |
Draw a plot of potential energy of a pair of nucleons as a function of their separation. What is the significance of negative potential energy in the graph drawn ? |
Answer» Solution :Plot of potential energy of a PAIR of nucleons as a FUNCTION of a their separation r has been SHOWN in Fig. 13.06. For `r gt r_(0)` the FORCE is attractive but for `r lt r_(0)` the nuclear force is strongly repulsive.  The negative potential energy signifies that the nucleons are in a state of stable equilibrium because force between them is attractive and their energy is least possible. |
|
| 41125. |
A plane electromagnetic wave Ez = 100cos (6xx10^8t+ 4x)V/m propagates in a medium. Find the refractive index of the medium. |
|
Answer» Solution :Comparing with the equation, `E=E_0 COS (omegat+kx)` we get , `omega=6xx10^(8) s^(-1),k=4m^(-1)` `THEREFORE` The velocity of the electromagnetic wave in the MEDIUM `v=omega/k=(6xx10^8)/4=1.5xx10^8 m.s^(-1)` The refractive index of the medium , `mu=c/v=(3xx10^8)/(1.5xx10^8)=2` |
|
| 41126. |
A magnet of m magnetic moment is rotate up to 360^@ in magnetic field H then the work done is…………… |
|
Answer» Solution :`W=mH(costheta_1-COS theta_2)` `=mH(cos 0^@-cos 360^@)` `=mH(1-1)` =0 |
|
| 41127. |
Does the size of mirror affect the nature of the image ? |
|
Answer» |
|
| 41128. |
A radiation of energy E falls normally on a perfectly reflecting surface. The momentum transferred to the surface |
|
Answer» E/C |
|
| 41129. |
Assertion:- Electric field produced by changing magnetic field is nonconservative. Reason:- For theelectric field vecE induced by a chagning magnetic field which has closed lines of force ointvecE.dveclcanel=0. |
|
Answer» If both Assertion `&` Reason are True `&` the Reason is a correct explanation of the Assertion. `ointvecE_("Induced").vecdl=(dphi_("magnitude"))/(dt)` |
|
| 41130. |
The apparent depth of water in cylindrical water tank of diameter 2R сm is reducing at the rate of x cm/minute when water drained out at a constant rate. The amount of water drained in c.c. per minute is (n_1= refractive index of air, n_2= refractive index of water ) |
|
Answer» `X PI R^2 n_1//n_2` |
|
| 41131. |
S_(1) and S_(2) in List I represent coherent point sources, S represents a point source lambda = wavelength of light emitted by the sources. Fringe pattern is observed on the screen. Exclude the position of source while detecting the fringe pattern. |
|
Answer» |
|
| 41132. |
In above equation No. 304, the potential energy of the satellite is |
|
Answer» `-(GmM)/((R+h)^(2))` |
|
| 41133. |
Unpolarised light is incident on a plane glass surface. What should be the angle of incidence so that the reflected and refracted rays are perpendicular to each other? |
| Answer» Solution :For `i + R` to be EQUAL to `pi//2`, we should have tan `i_(B) = mu = 1.5.` This GIVES `i_(B) = 57^(@)`. This is the Brewster.s angle for air to GLASS interface. | |
| 41134. |
What will be the size of image as compared to the object in a rearview mirror of a car if the radius of curvature of the mirror is 1 m and the object is 4.5 m from the mirror? |
| Answer» SOLUTION :(1/10), image will be erect, VIRTUAL, diminished and at a distance 45 cm behind the MIRROR | |
| 41135. |
Water rises to height of 20mm in capillary tube hving cross sectional area A. If the area of the cross section of the tube is made A/4, then find the rise of height water. |
|
Answer» Solution :`(Delta_2)/(Delta_1) = (r_2^2)/(r_1^2)` `THEREFORE (A/4)/A = 1/4 = (r_2^2)/(r_1^2)` `therefore (r_2)/(r_1)` = 1/2` `therefore (r_1)/(r_2)` =2 For capillary RISE `h_1 r_1 = h_2 r_2` `therefore h_2 = (h_1 r_1)/r_2 = 20 XX 2 = 40 mm = 4cm` |
|
| 41136. |
The differential equation for linear S.H.M. of a particle of mass 2 g is d^2x/dt^2 +16 x=0. What is it's force constant ? |
|
Answer» SOLUTION :`(d^2x)/dt^2 =-k/mx` `k/m=16` `k=16xx2=32"DYNE"//CM.` |
|
| 41137. |
Assertion (A) : X - rays are generated when a beam of high energy electrons bombard a metal target. Reason (R ) : X - rays were discovered by Sir William Roeiitgen. |
|
Answer» If both assertion and rason are true and the reason is the correct explanation of the assertion. |
|
| 41138. |
The sun delivers 10^3W//m^2 of electromagnetic flux to the earth's surface, which is at a distance of 1.5xx10^(11)m from the sun. The whole incident electromagnetic flux is absorbed by the earth. The radiation force on the roof is |
|
Answer» `2.67xx10^-4N` `=("TOTAL POWER on roof ")/("VELOCITY of LIGHT")=(8xx10^4)/(3xx10^8)=2.67xx10^-4N` |
|
| 41139. |
The open organ pipe resonant with frequency 340Hz if velocity of sound is 340m/s. The minimum length of pipe is |
|
Answer» 1m |
|
| 41140. |
S_(1) and S_(2) are two loudspeakers with the same frequency of 165 Hz and acoustic output 1.2 xx 10 ^(-3) and 1.8 xx 10^(-3) watts respectively/ They vibrate in the same phase. P is a point at a distance 4m from S_(1) and3m from S_(2) What is the intensity of sound at P if S_(1) is turned off (S_(2)) on) |
|
Answer» |
|
| 41141. |
If a free electron is placed in the path of a plane electro magnetic wave, it will start moving along: |
|
Answer» CENTRE of earth |
|
| 41142. |
An explosion creates a shock wave. Find the initial velocity of the wave front when the air pressure is 200 times the atmospheric pressure, assuming that the front of the shock wave may be regarded as a discontinuity in the density. Take into account that at such pressures gamma = 1.8. |
|
Answer» `a = sqrt((gamma_a P_0)/(rho_0)) , y = p/(p_0) = 200 , alpha = (gamma_0 + 1)/(gamma_0 - 1) = 3.5` We obtain after some TRANSFORMATIONS: `u = sqrt((alpha y + 1)/(alpha -1) cdot (a^2)/(gamma_0)) = a sqrt(280/(1.4)) = a sqrt(200)`. |
|
| 41143. |
S_(1) and S_(2) are two loudspeakers with the same frequency of 165 Hz and acoustic output 1.2 xx 10 ^(-3) and 1.8 xx 10^(-3) watts respectively/ They vibrate in the same phase. P is a point at a distance 4m from S_(1) and3m from S_(2) How are the phase of the two waves arriving at P related? |
| Answer» | |
| 41144. |
a) Determine the 'eefective focal length' of the combination of the two lenses in Exercise 10, if they are placed 8.0 cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident ? Is the notion of effective focal length of this system useful at all ? b) A object 1.5 cm in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and the convex lens is 40 cm. Determine the magnification produced by the two-lens is 40 cm. |
|
Answer» Solution :b) Here, `h_(1)=1.5cm, u_(1)=40cm,m=?` `h_(2)=?` for the 1st lens, `(1)/(upsilon_(1))-(1)/(u_(1))=(1)/(f_(1))` `(1)/(upsilon_(1))=(1)/(P_(1))+(1)/(u_(1))=(1)/(30)-(1)/(40)=(1)/(120)` `upsilon_(1)=120cm` Magnitude of magnification produced by FIRST lens, `m_(1)=(upsilon_(1))/(u_(1))=(120)/(40)=3` The image formed by 1st lens as VIRTUAL object for the 2nd lens. `u_(2)=120-8=112cm, f_(2)=-20cm` `upsilon_(2)=?` As `(1)/(upsilon_(2))-(1)/(u_(2))=(1)/(f_(2)) rArr (1)/(v_(2))=(1)/(f_(2))+(1)/(u_(2))` `(1)/(v_(2))=(-1)/(20)+(1)/(112)` `v_(2)=(-112xx20)/(92)cm` Magnitude of Magnification produced by second lens `m_(2)=(v_(2))/(u)=(112xx20)/(92xx112)=(20)/(92)` Net magnification produced by the combination `m=m_(1)xxm_(2)` `=3xx(20)/(92)=(60)/(92)=0.652` `therefore"size of image "h_(2)="mh"_(1)` `=0.652xx1.5` `=0.98cm` |
|
| 41145. |
Match the following {:("(a) Amplitude","(e) Amplitude and angular frequency remains constant"),("(b) Frequency modulation ","(f) Digital transmission"),("(c) Phase modulation","(g) noise creeps in"),("(d) Pulse code modulation","(h) Stereophonic transmission"):} |
|
Answer» a-e,b-h,c-e,d-f |
|
| 41146. |
Refractive index of a prism is root_2. One side of prism is polished, if ray incidences at ......, then it will return back to its original path, refraction angle is 30^@ |
|
Answer» SOLUTION :From Snell.s law at Q, `n= ( sini)/(sinr)` `therefore sini=nsin r` `=sqrt2xxsin 30^@` `=sqrt2xx1/2=(1)/(SQRT2)` `therefore i=45^@` 
|
|
| 41147. |
Name the optoelectronic devide used to detect optical signals. |
| Answer» SOLUTION :PHOTODIODE | |
| 41148. |
A mass M kg is suspended by a weightless string. The horizontal force required to hold the mass at 60^(@) with the vertical is |
|
Answer» MG |
|
| 41149. |
The temperature of an ideal gas is increased from 120 K to 480 K. If at 120 K, the root mean square velocity of the gas molecules is v, then at 480 K, it will be |
|
Answer» 4v `therefore (v_(1))/(v_(2))=SQRT((T_(1))/(T_(2)))=sqrt((120)/(480))=sqrt((1)/(4))=(1)/(2)` `v_(2)=2""[because v_(1)=v]` |
|
| 41150. |
Two identical capacitors A and B are charged to the same potential and then made to discharge through resistances R_A and R_Brespectively, with R_AgtR_B |
|
Answer» A will REQUIRE greater time than B to DISCHARGE COMPLETELY. |
|



