Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 4451. |
The velocity of light in vacuum can be changed by changing ...... |
|
Answer» AMPLITUDE `n=c/v` (Where c constant) `therefore n prop 1/v` So, if medium is changed, n also changes and accordingly velocity also changes. |
|
| 4452. |
If A=(1,2,3,4)}, then which of the following are functions from A to itself? |
|
Answer» `f_1={(X,y): y=x+1)` |
|
| 4453. |
A given coin has a mass of 3.0g . Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other . For simplicity,assume that the coin is entirely made of ._(29)^(63)Cu atoms (of mass 62.92960 u) |
|
Answer» Solution :Mass defect in each copper nucleus `Delta m = 29 m_(p) + 34 m_(n) - M_(Cu)` `= (29 xx 1.00727 ) + (34 xx 1.00866) -62.929 60` `Delta m = 0.57567` U Energy required to separate all neutrons and protons in one nucleus (is binding energy) `= Delta mxx 931.5 "MeV"` `E_(b) = 0.57567 X 931.5 = 536.2 "MeV"` Number of atoms in the copper COIN : `N= (6.023 xx 10^(23) xx 3)/( 63) = 2.868 xx 10^(22)` `therefore` Total energy required to separate all neutrons and protons in the coin `E_(b) xx N ` `536.2xx 2.868 xx 10^(22) = 1.538 xx 10^(25) "MeV"` (with unit) |
|
| 4454. |
We have a charged conductor having a cavity. Electric field inside the cavity is _________and the electric potential inside the cavity is __________ . |
| Answer» SOLUTION :ZERO, same as on the SURFACE of CHARGED CONDUCTOR. | |
| 4455. |
When an AC voltage of 220 V is applied to the capacitor C |
|
Answer» the maximum voltage between plates is 220 V. Power applied to a circuit is, `LT P gt =V_"rms" I_"rms" COS phi` but for capacitive circuit `phi=90^@` `therefore lt P gt =V_"rms" I_"rms" cos 90^@=0` |
|
| 4456. |
A simple pendulum has a pariod T inside a lift when it is stationary. The lift is accelerated upwards with constant acceleration 'a'. The period : |
|
Answer» DECREASES As `T=2pi sqrt((l)/(g))`. So the TIME PERIOD decreases. Hence correct choiceis (a). |
|
| 4457. |
Are the paths of electrons straight lines between successive collisions (with the positive ions of the metal) in the (i) absence of electric field, (ii) presence of electric field ? |
| Answer» Solution :In the absence of EXTERNAL electric field, paths of free electrons between two successive COLLISIONS are straight but in the PRESENCE of external electric field, these paths are CURVED (or non LINEAR) in general. | |
| 4458. |
(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire. (b) The electric field components in the following figure are E_(x)=alphax, E_(y)=0, E_(z)=0, in which alpha=400N//Cm. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a=0.1 m. |
Answer» Solution :(a) CONSIDER an infinitely long straight charged wire of linear charge density `lambda`. To find electric field at a point P situated at a distance r from the wire by using Gauss. law consider a cylinder of length l and radius r as the Gaussian surface. 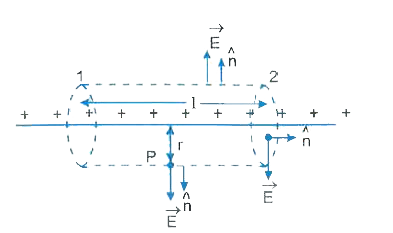 From SYMMETRY consideration electric field at each point of its curved surface is `vecE` and is pointed outwards normally. Therefore, electric flux over the curved surface `=intvecE.hatn ds=E 2pirl` On the SIDE faces 1 and 2 of the cylinder normal drawn on the surface is perpendicular to electric field E and hence these surfaces do not contribute towards the total electric flux. `therefore `Net electric flux over the entire Gaussian surface `phi_(E)=E.2pirl"....(i)"` By Gauss law electric flux `phi_(E)=(1)/(in_(0))"(charged enclosed)"=(lambdal)/(in_(0))"...(ii)"` Comparing (i) and (ii), we have `E.2pirl =(lambdal)/(in_(0))` `rArr""E=E=(lambda)/(2PI in_(0)r) and vecE=(lambda)/(2pi in_(0)r)hatr` (b) (i) Here, `E_(x)=alpha. x=400x, E_(y)=E_(z)=0 and a=0.1m`. So the electric flux is linked with only two fa c es of the cube lying in Y -Z plane (i.e., perpendicular to `E_(x)`). As position of left face of cube is at `x=a=0.1m`, hence `(E_(x))_(1)=400xx0.1=40NC^(-1)` (inward into the Cube) Now position of right face of cube is `x=a+a=2a=0.2m`, hence `(E_(x))_(2)=400xx0.2=80NC^(-1)`. `therefore"flux "phi_(2)=(E_(x))_(2).A^(2)=80xx0.01=0.8Nm^(2)C^(-1)" (outward)"` `therefore` Net flux `phi_(2)=(E_(x))_(2.)A^(2)=80xx0.01=0.8Nm^(2)C^(-1)" (outward)"` `therefore` Net flux through the cube `phi_(E)=phi_(2)-phi_(1)=0.8-0.4=0.4Nm^(2)C^(-1)` outward (ii) Charge within the cube `q=in_(0).phi_(E)=(8.854xx10^(-12))xx0.4=3.54xx10^(-12)C` |
|
| 4459. |
Which are two main points important for astronomical telescope ? |
|
Answer» Solution :The MAIN considerations with an astronomical - telescope are its light gathering power and its resolution or resolving power. The former clearly depends on the area of them objective. With larger diameters, fainter objects can be observed. The resolving power or the ability to observe TWO objects distinctly, which are in very nearly the same direction, ALSO depends on the diameter of the objective. So the desirable aim in optical telescopes is to make them with objective of large diameter. The largest lens objective in use has a diameter of 40 inch (- 1.02 m). It is at the Yerkes Observatory in Wisconsin, USA. Such big lenses tend to be very HEAVY and therefore, difficult to make and SUPPORT by their edges. Further it is rather difficult and expensive to make such large sized lenses which form images that are free from any kind of chromatic aberration and distortions. |
|
| 4460. |
Given an equilateral triangle with side L, find E at its centroid. The linear charge density is as shown in figure. |
Answer» Solution :The electric FIELD strength due to the threerods AB, BC and CA are shown in figure.  `barE_(AC) =(3lambda)/(2PI in_(0)L)` (towards B) `barE_(AB) =(3lambda)/( 2pi in_(0)L)` (towards C) `barE_(BC)=(3lambda)/(2pi in_(0)L)` (towards MIDPOINT of BC) `barE_("Net") = barE_(AC) +barE_(AB) +barE_(BC)` `=(3lambda)/(pi in_(0)L)` (towards midpoint of BC) |
|
| 4461. |
A batsman hits a pitched cricket ball at a height of 1.2 m above the ground so that it's angle of projection is 45^@ andit's horizontal range is 110m. The ball is lifted towards the left field line, where a fence of 7.5 m is located 100m from the position of batter. will the ball clear the fence ? |
|
Answer» yes x = 110m, y = 1.2m, `theta` = `45^@` u = 32.66/s Further `y = 100tan45^@ - (9.8xx(100)^2)/(2.(32.66)^2 cos 45^@) = 8.13 m ` TOTAL height 8.13 + 1.2 = 9.33 m > 7.5. |
|
| 4462. |
The earth's field, it is claimed, roughly approximates the field due to a dipole of magnetic moment 8 xx 10^(22) JT^(-1) located at its centre. Check the order of magnitude of this number in some way. |
|
Answer» Solution :Using the formula for field B on the normal bisector of a dipole of magnetic moment , we find `|vecB_E| = (mu_0)/(4pi)* (|vecm|)/(R^3)` Taking `m= 8 XX 10^(22) J T^(-1) , r ` (radius of EARTH) = `6.4xx10^6` m, we get `B_E = 3 xx 10^(-5)` , which resembles with the order of magnitude of the observed field on the earth . Thus, claim that earth.s field is DUE to a dipole of magnetic moment `8 xx 10^(22)` J `T^(-1)` is true. |
|
| 4463. |
While entering a paramagnetic material from air , the spacing between the magnetic lines of force |
|
Answer» REMAINS the same |
|
| 4464. |
What should be the energy of a conventional accelerator for it to be able to do the work of a colliding-beam accelerator of 200 MeV? Do the calculations both for electrons and for protons. |
|
Answer» |
|
| 4465. |
Assertion: Acceleration of a charged particle in non uniform electric field does not depend on velocity of charged particle Reason:Charge is an invariant quantity, that is,amount of charge on particle does not depend on frame of reference. |
|
Answer» Both ASSERTION and REASON are TRUE and Reason is the correct EXPLANATION of Assertion |
|
| 4466. |
Discuss the special cases on first minimum in Fraunhofer diffraction. |
|
Answer» Solution :Consider the condition for first minimum with (n = 1). a sin `theta = lamda` The first minimum has an angular spread of, `sin theta = lamda/a` Now, we have special cases to discuss on the above condition. (i) When `a lt lamda`, the diffraction is not possible, because `sin theta` can never be greater than 1. (ii) When `a gt= lamda` the diffraction is possible. (a) For `a = lamda, sin theta = 1 i.e., theta = 90^@` . That means the first minimum is at `90^@`. Hence, the central maximum spreads fully in to the geometrically shadowed region leading to bending of the diffracted light to `90^@` . (b) For `a gt gtlamda, sin theta lt lt1` i.e, the first minimum will fall within the width of the slit itself. The diffraction will · not be noticed at all. (III) When `agtlamda` and also comparable, say `a = 2 lamda, sin theta =lamda/a = (lama)/(2 lamda) = 1/2` ` theta= 30^@` These are practical cases where diffraction could be observed effectively. (iv) The slit AB is divided into two half's AC and CB. Now the width of AC `(a/2)`. Different points on the slit whichare separated by the same width(here ` a/2` ) called corresponding points. (v)The path difference of light waves from different corresponding points meeting at POINT P and interfere destructively to make it first minimum. The path difference `delta` between waves from these corresponding points is, `delta = a/2 sin theta` (vi) The condition for P to be first minimum, ` a/2 sin theta = lamda/2` ` a sin theta = lamda ` (first minimum) . |
|
| 4467. |
A point object is kept at a distance of 2m from origin on x- axis. A quarter cylinder of radius R=30 cm and refractive index mu=1.5 having its axis _|__(r) to plane of paper is placed between the object and the parabolic reflector at a distance of 130cm from origin as shown in figure. The position of the image after reflection from the parabolic reflector y^(2)=2x is 25lamdacm. Find the value of lamda? |
|
Answer» `tan(pi-theta)=-1/((DY)/(dx)|_((x_(1),y_(1))))=y_(1)` `tan2theta=(2tantheta)/(1-tan^(2)theta)=(y_(1))/(x_(2)-x_(1))` `impliesx_(2)=1/2m=50cm` 
|
|
| 4468. |
Two sound sources S_1 and S_2 emit pure sinusoidal waves in phase. If the speed of sound is 350 m/s, (a) For what frequencies does constructive interference occur at P? (b) For what frequencies does destructive interference occur at P? |
|
Answer» Solution :Path difference `Delta x = S_1P - S_2P` `=sqrt((2)^2 +(4)^2) - sqrt((1)^2 + (4)^2)` `=4.47 - 4.12 = 0.35m` (a) Constructive interference occurs when the path difference is an integer NUMBER of wavelength. `or Deltax = nlambda = (XV)/(f) or f = (n (v))/(Deltax)` where n = 1,2,3 ...... `:. f = (350)/(0.35), (2 xx 350)/(0.35), (3 xx 350)/(0.35),`....... `f = 1000Hz, 2000 Hz, 3000 Hz,...,` ETC. (b) Destructive interference occurs when the path difference is a half-integer number of wavelengths `Deltax = (2 n +1) lambda/2 n =0, 1,2,...(or ) Deltax = (2n +1) v/(2F)` `:.f = ((2n +1)v)/(2Deltax) =350/(2 xx 0.35) , (3 xx 350)/(2xx 0.35) , (5xx350)/(2 xx 0.35)`...... = 500 Hz, 1500 Hz, 2500 Hz |
|
| 4469. |
When the pollen grain is mature it contains two cells, the vegetative cell and generative cell. The vegetative cella. Is biggerb. Spindle shaped C. Has abundant food reserved. Has large irregularly shaped nucleus. |
| Answer» Answer :B | |
| 4470. |
Hot water cools from 60^(@)C" to "50^(@)C in the first 10 min and to 42^(@)C in the next 10 min. Then the temperature of the surroundings is: |
|
Answer» `20^(@)C` `(theta_(2)-theta_(1))/(t) =K [(theta_(1)+theta_(2))/(2)-theta_(s)]` where, `theta_(s)` is the temperature of the surroundings. `(60-50)/(10) =K [(60+50)/(2)-theta_(s)]` `1=K [55-theta_(s)]"….(i)"` Similarly, `(50-42)/(10) =K(46-theta_(s))` `(8)/(10)=K(46-theta_(s))"...(ii)"` Dividing Eq. (i) by Eq. (ii), we GET `(10)/(8) =(K(55-theta_(s)))/(K(46-theta_(s)))` `rArr theta_(s)=10^(@)C` So, correct choice is (d). |
|
| 4471. |
For diatomic gas, molar specific heat at constant volume is : (R = 2 cal/mol K) |
|
Answer» 3 cal/mol `_^@K` |
|
| 4473. |
In process 2, total energy dissipated across the resistance E_D is - |
|
Answer» ` E_D =3 ( (1)/(2) CV_0^(2) ) ` |
|
| 4474. |
Copper and Germanium are cooled from room temperature to 100 K . Then the resistance of |
|
Answer» Germanium decreases , COPPER increases |
|
| 4475. |
a.What isimpact parameter? b. Howis itrelatedto scatteringangle ? |
|
Answer» Solution :a. Impactparameter(b)of an` ALPHA ` - PARTICLE is theperpendiculardistanceof thevelocityvectorof the ` alpha `- particlefromthe CENTREOF thenucleus, whenit isawayfromthe nucleuus b.Scatteringangle`= theta `,impactparametere = b `cot ((theta )/(2)) =((4 pi epsi_0 T )/(Ze^2))b` |
|
| 4476. |
A monochromatic light source of intensity 5 m W emits (8x10^15) photons per second . This light ejects photoelectrons from a metal surface. The stopping potential for this setup is 2.0 V. Calculate the work function of the metal. |
|
Answer» Solution :`P= 5 X 10^(-3)W` `E=p/n=6.25 xx 10^(-19)J` `E=3.8eV` `W_(0)=E-eV_(0)` `=(3.9-2)eV_(0)` `W_(0)=1.8eV` |
|
| 4477. |
particle of mass m, moving with velocity 'u' makes head on collision with identical stationary particle, which is elastic. Theforce of interaction increases to maximum and then becomes zero in time 'T' as shown in graph. What is the maximum value F_(0) of interaction force ? |
|
Answer» Solution :1) Force REACHES MAXIMUM value in `T/2` time. The impulse of maximum force is `=F_(0) XX T/2` Since, impulse = Change in MOMENTUM, mu =`F_(0).T/2` i.e. `F_(0) =(2mu)/T` |
|
| 4478. |
An electrical element X, when connected to an ac sources has a current through it leading the voltage by pi/2 radian. Identify X and write an expression for its reactance. |
| Answer» SOLUTION :CAPACITOR , capacitative REACTANCE `X_C=1/C_omega`. | |
| 4479. |
A ship A is moving Westwards with a speed of 10kmh^(-1) and a ship B 100 km South of A, is moving Northwards with a speed of 10kmh^(-1). The time after which the distance between them becomes shortest,is |
|
Answer» `5sqrt2h` |
|
| 4480. |
A mark at the the bottom of a liquid appears to rise by 0.1 m. The depth of the liquid is lm. The refractive index of the liquid is |
|
Answer» 1.33 |
|
| 4481. |
Davission and Germer established wave nature of electrons by observing : |
|
Answer» REFRACTION of electrons |
|
| 4482. |
The structure that helps in photosynthesis in bacteria is |
|
Answer» Mitochondria |
|
| 4483. |
""_(1)^(2)H+""_(1)^(2)H to ""_(2)^(3)He+X Q. Identify the particle X resulting from the nuclear reaction show above. |
|
Answer» Positron |
|
| 4484. |
The primary of transformer carries a current of 10A due to which a magnetic flux of 10^-4Wb is created through its secondary. If the number of turns in the secondary is 25 . The mutual induction of the coil is: |
|
Answer» 5mH |
|
| 4485. |
A boat moves relative to water with a velocity which is 'n' times the river flow (a) If n < 1 boat can not cross the river (b) If n = 1 boat can not cross the river without drifting (c)If n > 1 boat can cross the river along shortest path (d) Boat can cross the river what ever is the value of n excluding zero value. |
|
Answer» only a is correct |
|
| 4486. |
What is the radiation pressure 2.7 m away from a 315 W lightbulb ? Assume that the surface on which the pressure is exerted faces the bulb and is perfectly absorbing and that the bulb radiates uniformly in all directions . |
| Answer» SOLUTION :`1.1xx10^(-8) ` PA | |
| 4487. |
The frequency f of certain line of the Lyman series of the atomic spectrum of hydrogen satisfies the following conditions: (i) it is the sum of the frequencies of another Lyman line and a Balmer line, (ii) it is the sum of the frequencies of a Lyman line, a Balmer line and a Paschen line, (iii) it is the sum of the frequencies of a Lyman and a Paschen line but no Brackett line. To what transition does f correspond? |
|
Answer» `n_(2)=3 to n_(1)= 1` |
|
| 4488. |
The kinetic energy E_(k) of a photoelectron varies withthe frequency upsilon of the incident radiation as which of the following ? |
|
Answer»
|
|
| 4489. |
The dispersive powers of crown and flint glasses are 0.03 and 0.05 respectively, The refractive indices for yellow light for these glasses are 1.517 and 1.621 respectively. It is desired to from an achromatice combination of prisms of crown and flint glasses which can produce a deviation of 1^@ in the yellow ray. Find the refracting angles of the two prisms needed. |
|
Answer» Solution :Suppose, the ANGLE of the CROWN prism needed is A and that of the filnt prism is A' We have `OMEGA = (mu_(upsilon) - mu_r)/(mu -1)` or, `mu_upsilon - mu_r = (mu -1)omega.` The angular dispersion produced by the crown prism is `(mu_(upsilon -1)omega A.` Similarly, the angular dispersion produced by the flint prism is `(mu' - 1) omega' A'` For achromatic combination, the NET dispersion should be zero. THUS, (mu - 1)omegaA = (mu' -1)omega'A` or `(A')/(A) = ((mu -1)omega)/((mu' - 1)omega') = (0.517 xx 0.03)/(0.621 xx 0.05) = 0.50. ... (i)` The deviation in the yellow ray produced by the crown prism is `delta = (mu -1)A` and by thecombination is `delta - delta' = (mu -1)A - (mu' - 1)A'` or , `1^@ = 0.517 A - 0.621 A'. .... (ii)` Solving (i) and (ii), `A = 4.8 ^@` and A' = 2.4^@.` Thus, the crown prism should have its refracting angle `4.8^@` and that of the flint prism should be `.2.4^@.` |
|
| 4490. |
The sensitivity of a galvanometer is 60 divisions/Amp. When a shunt is used, its sensitivity becomes 10 divisions/amp. If galvanometer is of resistance 20Omega, · the value of shunt used is : |
|
Answer» `4OMEGA` |
|
| 4491. |
Resistor of resistance R and a capacitor of capacitance Care connected in series to a battery of emf E, through a switch and this circuit is called A. Similarly, inductor of inductance L and resistor of resistance R are connected in series to a battery of emf Ethrough a switch and this circuit is called B. Switches in both the circuits A and B are closed at t= 0. |
|
Answer» CURRENT in circuit A is `E//R` just after t = 0 When LR circuit is switched on then at t = 0 inductor behaves like an infinite resistance and hence initial current in the circuit B becomes zero. Hence, option (c) is correct. After a long time when growth of the current is completed then inductor behaves like a zero resistance and final current `E//R` is established in the circuit B. Hence, option (d) is correct. |
|
| 4492. |
A metal wire is suspended vertically from a rigid support. When loaded with a weight in air, it extends by 0.4 mm and when the weight in air, it extends by 0.4 mm and when the weight is immersed completely in water, the extension is reduced to 0.2 mm. Then the relative density of the material of the suspended weight is |
| Answer» Solution :`(rho_(1))/(rho_(1)-rho_(2))=(l_(1))/(l_(1)-l_(2))=(0.4)/(0.4-0.2)=2`. | |
| 4493. |
A short bar magnet of magnetic moment m=0.32 JT^(-1) is placed in a uniform magnetic field of 0.15 T. If the bar is free to rotate in the place of the field , which orientation would correspond to its (a) stable , and (b) unstable equilibrium ? What is the potential energy of the magnet in each case ? |
|
Answer» Solution :`m=0.32JT^(-1),b = 0.15T` a. The bar MAGNET is directed ALONG the direction of external field so that PE is MINIMUM , `U = - mB = -4.8 xx10^(-2)J` (most stable ) b. Any other position , other than the above is UNSTABLE. The one with maximum PE is with the field antiparallel to that of the magnet . In this case. `U_(max)=mB=4.8xx10^(-2)J` |
|
| 4494. |
There is a convex lens of focal length 20 cm and a point object is placed at a distance 30 cm to the left of the lens. Radius of the lens is 5 cm. A person has placed eye at the right of lens at a distance 75 cm from the lens and at a height h below the principal axis. What can be the maximum value of h so that person is able to see the image ? |
|
Answer» 1.25 cm `(1)/(v)-(1)/(u)=(1)/(f)` `rArr""(1)/(v)-(1)/((-30))=(1)/(20)` `rArr""(1)/(v)=(1)/(20)-(1)/(30)=(3-2)/(60)` `rArr""v=+60cm` HENCE image is formed at a distance 60 cm to the right of the lens. Refer to the below given figure to calcualte height of eye below principal axis so that light RAY refracted from the top point of lens is able to pass through the eye so that image of the point object is visible to the person. 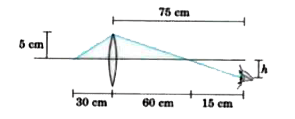 `(5)/(60)=(h)/(15)` `rArr""h=1.25cm` Hence, option (a) is correct. |
|
| 4495. |
Which Physical quantities have the same dimension ML^(2)T^(-2)? |
| Answer» SOLUTION :STRESS, YOUNG's MODULUS and PRESSURE. | |
| 4496. |
(a) Obtain the expression for the magnetic energy stored in a solenoid, due to the current I flowing in it, in terms of magnetic field B, area of cross-section A and length l of the solenoid. (b) How is this magnetic energy per unit volume compared with the electrostatic energy per unit volume stored in a parallel plate capacitor ? |
|
Answer» Solution :(a) We know that a solenoid having self-inductance L carrying current I has magnetic energy stored in it whose value is given by `U_(B) = 1/2 Ll^(2)` As magnetic field developed INSIDE the solenoid is `B = mu_(0)n^(2)I` hence `I=B/(mu_(0)n)`. Moreover self-indutance of solenoid coil `L = mu_(0)n^(2)Al`. Substituting these values, we have `U_(B) = 1/2 (mu_(0)n^(2)Al)(B/(mu_(0) n))^(2) = 1/(2mu_(0)).AlB^(2)` (b) As V = A.l is the volume of solenoid coil, hence magnetic energy stored per unit volume in a current carrying solenoid is given by `u_(B) = (U_(B))/V(1/(2mu_(0))AlB^(2))/(Al) = B^(2)/(2mu_(0))` The result compares with the ELECTROSTATIC energy per unit volume stored in a PARALLEL plate capacitor `u_(B)=1/2=in_(0)E^(2)` in the sense that in both cases energy per unit volume is proportional to square of electric/magnetic field. |
|
| 4497. |
A small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done ( by an external agent) in doing this is |
|
Answer» mgh, for all VALUES of H |
|
| 4498. |
What is potential difference between two points? What is it's unit and dimensions ? |
|
Answer» |
|
| 4499. |
Figure 2-6a is an x(t) plot for an elevator cab that is initially stationary, then moves upward ( which we take to be the positive direction of x ), and then stops. Plot v(t). |
|
Answer» Solution :KEY IDEA We can find the velocity at any timefrom the slope of the `x(t)` curve at that time. Calculations : The slope of `x(t)`, and so also the velocity, is zero in the intervals from 0 to 1 s and from 9 s on, so then the cab is stationary. During the interval bc, the slope is constant and nonzero, so then the cab moves with constant velocity . We calculate the slope of `x(t)` then as `(Delta x)/(Delta t) = v = ( 24 m - 4.0 m)/(8.0 s - 3.0 s)` ` = + 4.0 m//s` (2-5) The plus SIGN indicates that the cab is moving in the positive x direction. These intervals ( where `v=0` and `v=4` m/s) are plotted in Fig. 2-6 b. In addition, as the cab Figure 2-6 (a) The x(t) curve for an elevator cab that moves upward along an x axis. (b) The v(t) curve for the cab. Note that it is the DERIVATIVE of the x(t) curve ( `v = d x // dt`). (c) The `a (t)` curve for the cab . It is the derivativeof the `v(t)` curve ( a = dv/dt). The stick FIGURES along the bottom suggest how a passenger.s body might feel during the accelerations. initially beging to move and then later slows to a stop, v varies as indicated in the intervals 1 s to 3s and8 s to 9s. THUS, Fig. 2-6 b is the required PLOT. ( Figure 2-6c is considered in Section 2.6 ) Given a v(t) graph such as Fig. 2-6 b, we could " work backward" to produce the shape of the associated `x(t)` graph (Fig. 2-6a). However, we would not know the actual values for x at various times, because the v(t) graph indicates only changes in x. To find such a change in `x` during any interval, we must, in the language of calculus, calculate the area " under the curve" on the v(t) graph for the that interval. For example, during the interval 3s to 8 s in which the cab has a velocityof 4.0 m/s. the change in `x` is `Delta x = ( 4.0 m//s) (8.0 s - 3.0 s) = + 20 m`. (2-6) (The area is positive because the v(t) curve is above the t axis. ) Figure 2-6a shows that `x` does indeed increase by 20 m in that interval. However, Fig. 2-6 b does not tell us the values of `x` at the beginning and end of the interval. For that, we need additional information, such as the value of `x` at some instant. |
|
| 4500. |
A fish in a water tank sees the outside world as if it (the fish) is at the vertex of cone such that the circular base of the cone coincides with the surface of water. Given the depth of water where fish is located being h and the critical angle for water-air interface being ic, find out by drawing a suitable ray diagram the relationship between the radius of the cone and the height h. |
Answer» Solution :The ray diagram is shown in Fig. 9.41. Here B is a FISH SITUATED at a depth from the WATER surface and R is the radius of the cone. By definition of critical angle, we have: `sin i_( C) =1/n`, where n is the refractive index of water  But, `sin i_( C) = (CA)/(BA) = R/sqrt(R^(2) + H^(2))` Hence, `1/n = R/sqrt(R^(2) + h^(2)) rArr R =h/sqrt(n^(2)-1)` |
|



