94420 + Interview Questions in Chemistry in Class 12 Page 1860 InterviewSolution

92951.	1150 kcalheat is relasedwhen followingreaction is carriedout constant volume 27^(@)C_(7)H_(16)(l)+11O_(2)(g)to7CO_(2)(g) +8H_(2)(l)Find the heat changeatconst power .
Answer» SOLUTION :N//A

Discussion

92952.	11.2L of a gas at STP weighs 14g. The gas could be:
Answer» `N_(2)O` `NO_(2)` `N_(2)` `CO` ANSWER :C::D

Discussion

92953.	._11^24Na(half-life=15hrs.)is known to contain some radioactive impurity (half-life=3hrs.) in a sample. This sample has an intial activity of 1000 counts per minute, and after 30 hrs it shows an activity of 200 counts per minute. what percent of the intial activity was due to the impurity ?
Answer» 10 40 5 20 Solution :Let the activity due to IMPURITY be 'a' cpm `:.` due to NA it is (1000-a) cpm. After 30 hrs 'a' would be REDUCED to `(1/2)^10` a cpm and (1000-a) would be reduced to `1/4` (1000-a)cpm `:.` TOTAL activity after 30 hrs would be `(10/2)^10 a+1/4(1000-a)=200`(given) SOLVING we get `250-1/4a=200` `therefore 1/4a=50 implies a=200` Hence 20% activity was due to impurity.

Discussion

92954.	11.2L of a gas at STP weighs 14g. The gas could be
Answer» `N_(2)` CO `NO_(2)` `N_(2)O` ANSWER :A::B::C::D

Discussion

92955.	""_(11)^(23)Na ismore stable isotope of Na. Find out the process by which ""_(11)^(24)Na can undergo radioactive decay:
Answer» `BETA`-EMISSION `ALPHA`-emission `beta^(+)` emission K-electron capture Answer :A

Discussion

92956.	1,1,2,2 -Tetrabromoethane whenheated withzincand alcoholgives :
Answer» ETHANE ETHYLENE acetylene None of these ANSWER :C

Discussion

92957.	1,1,2,2- tetrachloropropane was heated with zinc dust and the product was bubbled through ammonical AgNO_3. What is the weight of precipitate obtained?
Answer» 30.0g 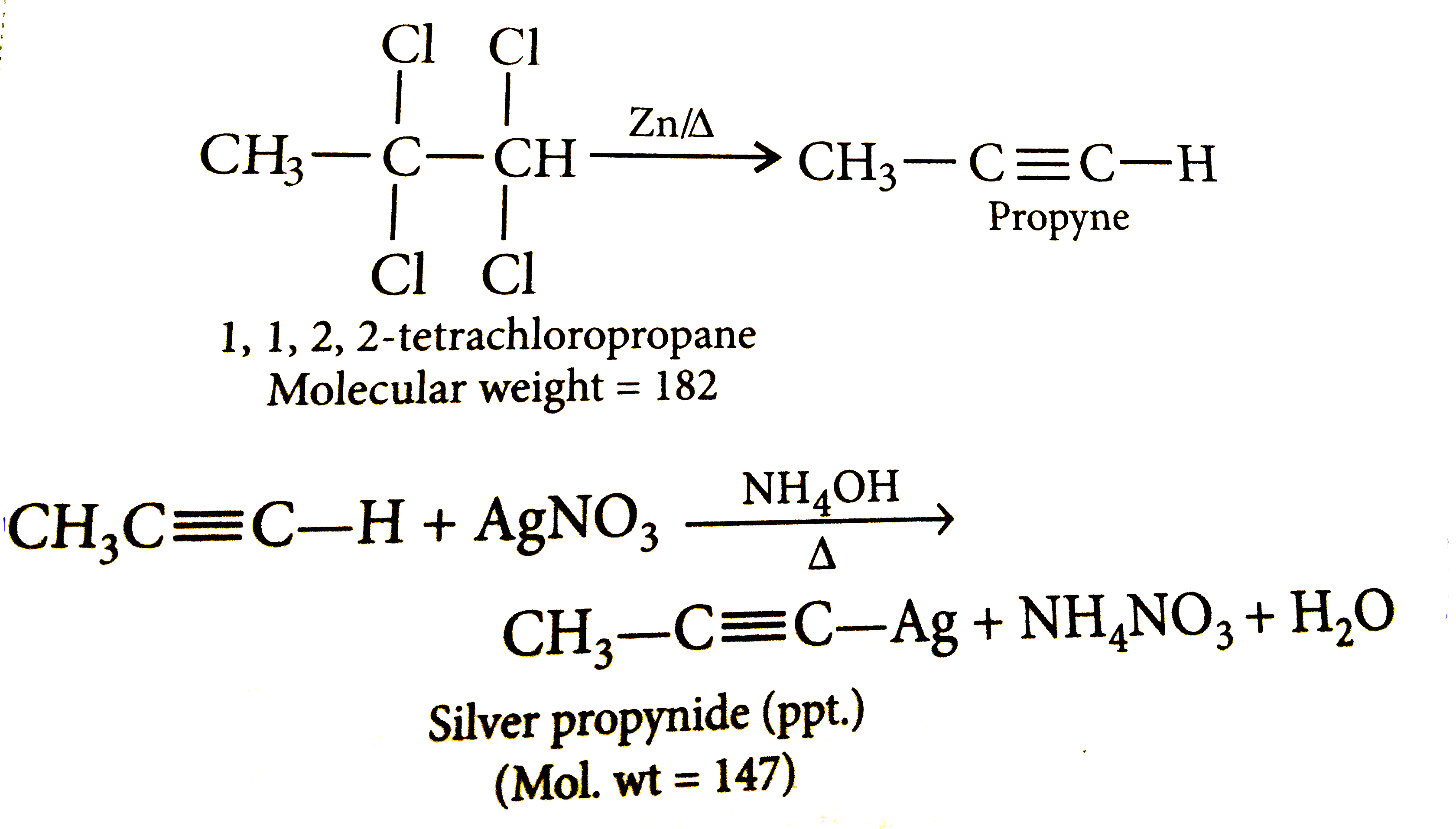29.4g 28.0g 25.7g Solution :The dehalogenation of vicinal tetrahaloalkane gives alkynes. It is done by heating the compound with ZN dust. `:'` 182 g of tetrachloro ALKANE gives 147 gives 147 g of PPT. `:.` 36.4g of tetrachloro alkane gives `(147xx 36.4)/182` = 29.4 g of precipitate

Discussion

92958.	1,1,2,2-tetra bromo ethane on heating with Zn powder in alcohol finally gives:
Answer» METHANE Ethane Ethyne Ethene Answer :A

Discussion

92959.	1.12 litre dry chlorine gas at STP was passed over a heated metal when 5.56 g of chloride of the metal was formed. What is the equivalent weight of the metal ?
Answer» ANSWER :20.1

Discussion

92960.	11.1g. Of CaCl_(2) is present in 100 ml of the aqueous solution. The chloride ion concentration is
Answer» 1M 2M 0.5M 0.2M ANSWER :B

Discussion

92961.	1.1 mole of A are mixed with 2.2 mole of Band the mixture is then kept In one litre flask till the equiliberium is attained A + 2B ⇌ 2C + D. At the equiliberium, 0.2 mole of C are formed. The equiliberium constant of the rection is :
Answer» 0.001 0.002 0.003 0.004 Answer :A

Discussion

92962.	1.1 mole of A are mixed with 2.2 mole of B and the mixture is then kept in a 1 L vessel till the equilibrium :A+2B hArr 2C+Dis reached.At equilibrium 0.2 moles of C are formed.The equilibrium constant for the reaction is :
Answer» `0.001` `0.002` `0.003` `0.004` SOLUTION :`K=([C]^(2)[D])/([A][B]^(2))` `[C]=0.2[D]=0.1, [A] =1.1-0.1=1.0`, `[B]=2.2-0.2=2.0` `therefore K=((0.2)^(2)(0.1))/((1.0)(2.0)^(2))=0.001`

Discussion

92963.	1.1 g CH_3(CH_2)_n COOHwas burnt in excess of air and the resultant gases (CO_2 + H_2O)were passed through a solution of NaOH. The resulting solution is divided into two equal parts. One part required 75 m.e. of HCl for neutralisation using phenolphthalein as indicator. The other part required 100 m.e. of HCI using methyl orange as indicator, Find n.
Answer» ANSWER :2

Discussion

92964.	11 g ,3 g
Answer» 11 G, zero 1 g,3 g 14 g,3 g 11 g ,3 g Answer :C

Discussion

92965.	1,1-dichloroethane on boiling with KOH(aq.) yields :
Answer» ACETONE ETHANOL Glycol Ethanal Answer :D

Discussion

92966.	1,1 - dichlorocyclohexane on alkaline hydrolysis gives
Answer» CYCLOHEXANE carbaldehyde cyclohexanone benzophenone cyclohexane CARBOXYLIC ACID ANSWER :B

Discussion

92967.	1.0xx10^(-3) kg of urea when disso,ved in 0.0985 kg of a solvent, decreases freezing point of the solvent by 0.211K.1.6xx10^(-3) kg of another non-electrolyte solute when disso,ved of 0.086 kg of the same solvent depresses the freezing point by 0.34 K. 0.35 K. Calculate the molar mass of the another solute. (Given molar mass of urea = 60)
Answer» Solution :Given : MASS of SOLUTE, Urea `=W_(2)` `=10xx10^(-3)kg=1g` Mass of SOLVENT `=W_(2)` `=00985kG=985g` `:.""DeltaT=0211k` MOLAR mass of urea `(NH_(2)CONH_(2))` `=M_(2)=60g//mol` Mass of unknown sabstance `=W_(2)^(')=16xx10^(-3)kg` `=16g` Mass of a solvent `=W_(1)^(')=0086` kg `:.""deltaT_(F)=034k` Molar mass of unknown sabstance `=M_(2)^()=?` This problem will be done in two parts : (i) To calculate molal depression constant `'K_(f)'`, For urea solution- `DeltaT_(f)=K_(f)xx(W_(2)xx1000)/(W_(1)xxM_(2))` `:.""K_(f)=(DeltaT_(f)xxW_(1)xxM_(2))/(W_(2)xx1000)` `=(0211xx985xx60)/(1xx1000)` `=(124701)/(1000)=124701` `:.""K_(f)=12g//mol`. (ii) To calculate molar mass, `M_(2)` For unknown solution `M_(2)^(')=K_(f)xx(W_(2)^(')xx1000)/(W_(1)^(2)xx034)` `:.""K_(f)=(12xx16xx1000)/(84xx034)` `=(1920)/(2924)` `:.""M_(2)^(')=6566g//mol` Hence, the molar mass of abother solution is 6566 g/mol.

Discussion

92968.	10mL of hydrogen contains 2xx10^(3) molecules of hydrogen at certain pressure and temperature. Calculate the number of molecules of oxygen whose volume is 200mL at the same temperature and pressure.
Answer» ANSWER :`4XX10^(4)` MOLECULES.

Discussion

92969.	10mL of hydrogen combine with 5 mL of oxygen to yield water. When 200 mL of hydrogen at NTP are passed over heated CuO, the CuO loses 0.144 g of its mass. Do these resutls correspond to the law of constant proportions?
Answer» SOLUTION :1ST case: Mass of 10mL HYDROGEN at NTP `=(2)/(22400)xx10=0.00089g` Mass of 5 mL of oxygen at NTP=`(32)/(22400)xx5=0.00714g` Ratio of masses of hydrogen and oxygen `=0.00089:0.00714=1:8` 2nd Case: Mass of 200mL of hydrogen at NTP `=(2)/(22400)xx200=0.0178g` Mass of oxygen LOST by CUO which actually combined with 0.0178g hydrogen at NTP to form water =0.144 g Ratio of masses of hydrogen and oxygen =0.00178:0.144 1=1:8`

Discussion

92970.	10ml of conc. H_(2)SO_(4) (18 molar) is diluted to 1 litre. The approximate strength of dilute acid could be
Answer» 0.18 N 0.09 N 0.36 N 1800 N Solution :`(H_(2)SO_(4))N_(1)V_(1)=N_(2)V_(2)` (dilute acid) `N_(2) = (10xx36)//1000=0.36 N`.

Discussion

92971.	10mg of an adsorbate gets adsorbed on a surface. This causes the release of 3J of heat at constant pressure and at 27^(ul@)C. [Molar mass of adsorbate = 100 g/mol]. (i) Find triangleH_("adsorption"). (ii) Argue whether the adsorption is physical or chemical ? (iii) If 20 mg of adsorbate is adsorbed at temperature T_(0). Then compare T_(0) and 27^(ul@)C :
Answer» SOLUTION :`T_(0) lt 27^(ul@)C`

Discussion

92972.	1.0M solution of a weak base, BOH is only 0.5% ionized. If 2mL 1 M solution of BOH is mixed with 30mL water, the degree of dissociation of the base in the resulting solution and H^(+) ion concentration of the solution will be respectivley.
Answer» 0.02 and `1.25 XX 10^(-3) M` ` 0.08 xx 3.5 xx 10^(-3) M` ` 0.04` and `3.0 xx 10^(-4) M` 0.0 2AND `8.0 xx 10^(-12) M` ANSWER :D

Discussion

92973.	10g solution of CuSO_4 is electrolyzed using 0.01F of electricity. Calculate : Equivalents of acid or alkali in the solution.
Answer» ANSWER :A::C::D

Discussion

92974.	10g sample of bleaching powder was dissolved into water to make the solution one litre. To this solution 35 mL of 1.0 M Mohr salt solution was added containing enough H_(2)SO_(4). After the reaction was complete, the excess Mohr salt required 30 mL of 0.1 M KMnO_(4) for oxidation. The % of availabel Cl_(2) approximately is (mol wt = 71)
Answer» ANSWER :0.071

Discussion

92975.	10g of hydrofluoric acid gas occupies 5.6 litre of volume at NTP. If the empirical of the gas is HF, then its molecular formula will be: (At. Mass of F=19)
Answer» HF `H_(3)F_(3)` `H_(2)F_(2)` `H_(4)F_(4)` SOLUTION :MOLECULAR mass `=(10)/(5.6)xx22.4=40`

Discussion

92976.	10g of a radioactive substance is reduced to 1.25 g after 15 days. Its 1kg mass will reduce to 500g in
Answer» 500 days 125 days 25 days 5 days Solution :`N = [(1)/(2)]^(n) xx N_(0)` `1.25 = [(1)/(2)]^(n) xx 10` `[(1)/(2)]^(n) = (1.25)/(10) = (1)/(8) = [(1)/(2)]^(3) , n = 3` Half-life time `= (15)/(3) = 5` days

Discussion

92977.	10g of a mixture of hexane and ethanol are reacted with Na to give 200mL of hydrogen at 27^(@)C and 760mmHg pressure. What is the percentage of ethanol in the mixture
Answer» SOLUTION :`2C_(2)H_(5)OH + 2NA rarr 2C_(2)H_(5)Ona + H_(2)`

Discussion

92978.	10g hydrogen and 64 g oxygen were filled in a steel vessel and exploded, Amoung of water produced in this reaction will be
Answer» 3 mol 4 mol 1 mol 2 mol Solution :`n_(H_(2))=(10)/(2)=5 n_(O_(2))=(64)/(32)=2` `2H_(2)+O_(2)rarr2H_(2)O` CaseI: If `H_(2)` is completely consumed, then `n_(H_(2)O)=5`mol CaseII: If `O_(2)` is completely consumed, then `n_(H_(2)O)=(2)/(1)xx2=4` mol Since,`O_(2)` gives least amount of product on complete consumption HENCE, it is limiting and number of moles of water formed will be equal TO4.

Discussion

92979.	10g farily concentrated solution of CuSO_(4), is electrolysed by passing 10 ampere current for 1.5 minutes calculate. (a) The weight of resulting solution (b) The number of equivalents of acid or alkalli produced in solution (Cu=63.5)
Answer» ANSWER :(a) 9.6294g (B) `9.326 XX 10^(-3)`

Discussion

92980.	10cm^(3) of 0.1N monobasic acid requires 15cm^(3) of sodium hydroxide solution whose normality is
Answer» 0.066 N 0.66 N 1.5 N 0.15 N Solution :From NORMALITY equation `N_(1)V_(1)=N_(2)V_(2)` or `N_(a)V_(a)=N_(b)V_(b)RARR N_(b)=(0.1xx10)/(15)`

Discussion

92981.	10cm^(3) of 0.1 N monobasic acid requires 15cm^(3) of sodium hydroxide solution whose normality is
Answer» 0.066 N 0.66 N 1.5 N 0.15 N Solution :From NORMALITY equation `N_(1)V_(1)=N_(2)V_(2) "" orN_(a)V_(a)=N_(B)V_(b)` `N_(b)=(0.1xx10)/(15)=0.066N`

Discussion

92982.	108Ã·7.2=14.583. The correct answer to this problem in proper number of significant digits is
Answer» `15` `14.58` `14.5` None of these Solution :`{:(108,Ã·7.2,=14.5833),("Three S.F. ","TWO S.F.",):}` Here answer should have two significant FIGURES. Therefore, CORRECT answer, after ROUNDING off two significant figures is 15.

Discussion

92983.	10800C of electricity past through the electrolyte deposited 2.977 g of metal with atomic mass106.4 g mol^(-1). Find the charge on the metal cations.
Answer» SOLUTION :`10800 E to 2.977 , " CHARGE " XX 96,500 to 106.4` `"Charge" xx 96,500 xx 2.977 = 106.4 xx 10800` Charge `=(106.4 xx 10800)/( 96500 xx 2.977) = 3.94 = 4 `

Discussion

92984.	10800 C of electricitythrough the electrolyte deposited 2.977 g of metal with atomic mass 106.4 g mol^(-1). Find the charge on the metal cations.
Answer» Solution :`M^(N+) + n e RARR M` For `M, (w)/(E) = (it)/(96500)"" ( :' Q = i XX t)` `(2.977)/(106.4//n) = (10800)/(96500)` `:. n = (106.4 xx 10800)/(2.977 xx 96500) = 4`

Discussion

92985.	10800 C of electricity passed through an electrolyte deposited 2.977 g of metal with atomic mass 106.4 " g mol"^(-1) The charge on the metal cation is :
Answer» `+ 4` `+3` `+2` `+1` ANSWER :A

Discussion

92986.	10800 C of electricity on passing through the electrolyte solution deposited 2.977g of metal with atomic mass 106.4 g mol^(-1) the charge on the metal cation is :
Answer» `+4` `+3` `+2` `+1` ANSWER :A

Discussion

92987.	10.6 g of a substance of molecular weight 106 was dissolved in 100 ml 10 ml of this solution was pipetted out into a 1000 ml flask and made up to the mark with distilled water. The molarity of the resulting solution is
Answer» 1M `10^(-2)M` `10^(-3)M` `10^(-4)M` Answer :B

Discussion

92988.	1.05 g of a lead ore containing impurity of Ag was dissolved in quantity of HNO_(3) and the volume was made 350 mL . A Ag electrode was dipped in the solution and E_(cell) of Pt(H_(2))\|H^(+) (1 M)\|\|Ag^(+)\|Ag was 0.503 V at 298 K. calculate % of lead in the ore. E_(Ag^(+)//Ag)^(@)=0.80 V
Answer» Solution :`{:("Anode "1/2H_(2)(G) rarr H^(+) (1 M)+e^(-)),("CATHODE "Ag^(+)(x)+e^(-) rarrAg(s)),(ulbar(1/2H_(2)(g)+Ag^(+) (x) hArr Ag(s)+H^(+) (1 M))""(n=1)):}` `E^(@)=0.80-0=0.80` volt `Q=([H^(+)])/([Ag^(+)])=1/x` `E=E^(@)-0.0591/n log_(10) Q` `0.503=0.80-0.0591/1 log_(10) (1/x)` `x=9.43xx10^(-6) M` Number of moles of `Ag^(+)` in 350 mL `=(MV)/1000=(9.43xx10^(-6)xx350)/(1000)` `=3.3xx10^(-6)` Mass of `Ag=3.3xx10^(-6)xx108=3.56xx10^(-4)g` % Ag in the ore`=(3.56xx10^(-4))/1.05xx100=0.0339 %`

Discussion

92989.	1.020 g of metallic oxide contains 0.540g of the metal . Calculate the equivalent mass of the metal and hence its atomic mass with the help of Dulong and Petit's law. Taking the symbol for the metal s M. find the molecular formula of the oxide. The specific heat of the metal is 0.216 cal "deg"^(-1) g^(-1).
Answer» SOLUTION :MASS of oxygen in the oxide `=(1.020-0.540)=0.480g` Equivalent mass of the metal `=(0.540)/(0.480)xx8=9.0` ACCORDING to Dulong and Petit's law, APPROX, atomic mass `=(6.4)/("Sp.heat")=(6.4)/(0.216)=29.63` Valency of the metal =`("At.mass)/("Eq.mass")=(29.63)/(9.0)=3` Hence, the FORMULA of the oxide is `M_(2)O_(3)`.

Discussion

92990.	1^(0),2^(0),3^(0) - amines can be distinguishedby using1) H_(2) O "" (2) R-X (3) HCl "" (4)(CH_(3)CO)_(2)O
Answer» `NaNO_(2) + HCl` `CH_(3) COCl` `C_(6)H_(5)SO_(2) Cl` ALLOF these Answer :D

Discussion

92991.	10.1g of a volatile liquid occupies a volume of 4 litres when vaporised at 100^(@)C and 70 cm pressure. What would be the osmotic pressure of a 2% (grams per 100 "cc") solution of this substance at 0^(@)C?
Answer» ANSWER :`5.34` ATM

Discussion

92992.	100mL of a solution containning 5 g of NaOH is mixed with 200 mL of M/5 NaOH solution. Calculate the molarity of the resuliting solution.
Answer» SOLUTION :Mass os NaOH in 200 mL of M/5 NaOH solution `"Molarity of solution"=("Mass os NaOH(W)/Molar mass")/("Volume of solution in LITRES")` `(1//5" mol L"^(-1))=W/((40" g mol"^(-1))XX(0.2L))` `W=(1//5" mol L"^(-1))xx(40" g mol"^(-1))xx(0.2 L)=1.6 g` Step II. Molarity of MIXTURE solution Total mass of NaOH = 1.6 + 5.0 =6.6 g Total volume of solution = 200 + 100 = 300 mL `"Molarity (M)"=("Mass os NaOH/Molar mass")/("Volume of solution is litres")=((6.6g)//(40" g mol"^(-1)))/((300//1000 L))` `0.55" mol L^(-1)=0.55 M`

Discussion

92993.	100ml of 0.01 M solution of NaOH is diluted to 1dm^(3). What is the pH of the diluted solution
Answer» 12 11 2 3 Solution :100 ML 0.01 M NaOH solution is DILUTED to `1 dm^(3)` (i.e., 10 times dluted) hence, the resultant solution will be 0.001 M. `:. [OH^(-)] = 0.001 = 10^(-3)` `[H^(+)] = (10^(-14))/([OH^(-)]) = (10^(-14))/(10^(-3)) = 10^(-11)` `because pH = - log[H^(+)] = -log[10^(-11)]` pH = 11.

Discussion

92994.	100mL of a clear saturated solution of Ag_(2)SO_(4) is added to 250mL of a clear saturated solution of PbCrO_(4) .will any precipitate form and if so what ?Given K_(sp) values of Ag_(2)SO_(4),Ag_(2)CrO_(4),PbCrO_(4)& PbSO_(4) are 1.4xx10^(-5),2.4xx10^(-12),2.8xx10^(-13) and 1.6xx10^(-8) respectively.
Answer» Solution :For `Ag_(2)SO_(4)hArr underset(2s)2Ag^(+)+underset(s)SO_(4)^(2-)` `K_(sp)=4S^(3)or s=3sqrt((K_(sp))/(4))=sqrt((1.4xx10^(-5))/(4))=1.52xx10^(-2)M` for `PbCrO_(4)hArr Pb^(2+)+CrO_(4)^(2-)` `K_(sp)=s_(1)^(2) or s_(1)sqrt(K_(sp))=sqrt(2.85xx10^(-13))=5.29x10^(-7)M` In solution concentration of each ION can be GIVEN as: THUS `[Ag^(+)]=(2sxx100)/(350)=(2xx1.52xx10^(-2)xx100)/(350)=0.869xx10^(-2)M` `[SO_(4)^(2-)]=(sxx100)/(350)=(1.52xx10^(-2)xx100)/(350)=0.43xx10^(-2)M` `[Pb^(2+)]=(s_(1)xx250)/(350)=(5.29xx10^(-7)xx250)/(350)=3.78xx10^(-7)M` `[CrO_(4)^(2-)]=(s_(1)xx250)/(350)=(5.29xx10^(-7)xx250)/(350)=3.78xx10^(-7)M` It is thus evidence that, `[Ag^(+)]^(2)[CrO_(4)^(2-)]=(0.869xx10^(-2))^(2)xx(3.78xx10^(-7))` `=2.85xx10^(-11)(gtK_(sp)Ag_(2)CrO_(4))` Thus `Ag_(2)CrO_(4)` will percipitate.

Discussion

92995.	1.00g of a non-electrolyte solute dissolved in 50g of benzene lowered the freezing point of benzene by 0.40K. Freezing point depression constant of benzene is 5.12K g//mol. Find the molar mass of solute. .
Answer» SOLUTION :`M_B= (1000K_f)/(DELTA T_f) W_B/W_A= (1000xx5.12)/0.4xx1/50 = 256G MOL^(-1)`

Discussion

92996.	1.00g of a non-electrolyte solute dissolved in 50g of benzene lowered by 0.40K. The freezing point depression constant of benzene is 5.12K kg//mol. Find the molar mass of solute.
Answer» SOLUTION :Molar MASS, `M_B= (1000K_f)/(Delta T_f) W_B/W_A= (1000xx5.12)/0.4xx1/50 = 256G mol^(-1)`

Discussion

92997.	100cm^(3) of an aqueous solution of BaCIU_(2)2H_(2)O is found to contain 6.022xx10^(22)CI^(-1)ilos. Calculate the molarity of the solution.
Answer» Solution :STEP I. Calculation of mass of `BaCI_(2)2H_(2)O` in the solution. Barium chloride is a strong electrolyte. It is completely ionised in solution. The number of different species in the solution may be represented as : `BaCI_(2)2H_(2)O(s)OVERSET(("aq"))toBa^(2+)("aq")+ 2CI^(-)("aq")+aH_(2)O` `(3.011xx10^(22)"molecules")""(3.011xx10^(22))""(6.022xx10^(22))` `"Gram molecular mass of "BaCI_(2)2H_(2)O=137.5+2xx35.5+2xx18=244" g mol"^(-1)` `6.022xx10^(23)" molecules of "BaCI_(2).2H_(2)O" correspond to mass"=244.5 g.` `6.022xx10^(23)" molecules of "BaCI_(2).2H_(2)O" correspond to mass"=((3.011xx10^(22)))/((6.022xx10^(23)))xx244.5 g=12.225 g.` Step II. Calculation of MOLARITY of the solution. `"Molarity of soltuion (M)"=("Mass of "BaCI_(2).2H_(2)O"/Molar mass")/("Volume of solution in Litres")=((12.225g)//(244.5"g mol"^(-1)))/((0.1 L))` `o.5 "mol L"^(-1)=0.5 M.`

Discussion

92998.	1000g of 1m aqueous solution of sucrose is cooled and maintained at -3.534^(@)C. Find how much ice will separate out. K_(f)(H_(2)O)=1.86Kkgmol^(-1)
Answer» Solution :Let m. be the molality of the solution after the ICE separates out at `-3.534^(@)C` Now we have, `DeltaT_(f)=K_(f)*m.` `:.m.=(DeltaT_(f))/(K_(f))=(3.534)/(1.86)=1.9` Let us now calculate the amount of ice separated. Initially the molality is 1m and wt. of solution is 1000g 1 mole of sucrose is dissolved in 1000g of `H_(2)O` or 342g of sucrose is dissolved in 1000g of `H_(2)O` `:.1342g` of solution contained `342g` of sucrose `:.1000g` of solution contained `(342)/(1342)xx1000=254.84g` Amount of `H_(2)O=1000-254.84=745.16g` Now, when ice separates out, the molality is 1.9 and the weight of sucrose remains the same as before `:.(1.9xx342)`g of sucrose is present in 1000g of `H_(2)O`. `:.254.84g` of sucrose should be in `(1000xx254.84)/(1.9xx342)` =392.18g of `H_(2)O` Thus amount of ice separated `=745.16-392.18` `=352.98g`

Discussion

92999.	1000 g of 1 m sucrose solution in water is cooled to -3.354^(@)C. What mass of ice would separated out at this temperature ? K_(f) for H_(2)O= 1.86" K mol"^(-1)kg.
Answer» Solution :`DeltaT_(f)=K_(f)xxm = 1.86 xx1=1.86^(@)` `therefore ` Freezing point of the solution `=-1.86^(@)C` As TOTAL mass of solution = 1000 G `therefore""w_(1)+w_(2)=1000"...(i)"` Further, `""DeltaT_(f)=(1000K_(f)w_(2))/(w_(1)xxM_(2))` `1.86xx(1000xx1.86xxw_(2))/(w_(1)xx342)"or"(w_(2))/(w_(1))=(1.86xx342)/(1000xx1.86)=0.342"...(ii)"` From eqns. (i)and (ii), on solving, we get`""w_(2)=254.84g` `""w_(1)=745.16g` These were the amounts present in the original solution UPTO -`1.86^(@)C`. Now on further cooling to `-3.534^(@)C`, mass of sucrose will remain the same but some water will freeze out as ICE. The mass of water left can be CALCULATED as follows : `DeltaT_(f)=(1000K_(f)w_(2))/(w_(1)xxM_(2))` `3.534=(1000xx1.86xx254.84)/(w_(1)xx342) or w_(1)=392.18 g` `therefore ` Amount of water separated as ice `=745.16-392.18 g = 352.98 g`

Discussion

93000.	1000 g aqueous solution of CaCO_3contains 10 g calcium carbonate. Hardness of the solution is:
Answer» 10 ppm 100 ppm 1000 ppm 10000 ppm Answer :D

Discussion

Explore topic-wise InterviewSolutions in .

1150 kcalheat is relasedwhen followingreaction is carriedout constant volume 27^(@)C_(7)H_(16)(l)+11O_(2)(g)to7CO_(2)(g) +8H_(2)(l)Find the heat changeatconst power .

11.2L of a gas at STP weighs 14g. The gas could be:

._11^24Na(half-life=15hrs.)is known to contain some radioactive impurity (half-life=3hrs.) in a sample. This sample has an intial activity of 1000 counts per minute, and after 30 hrs it shows an activity of 200 counts per minute. what percent of the intial activity was due to the impurity ?

11.2L of a gas at STP weighs 14g. The gas could be

""_(11)^(23)Na ismore stable isotope of Na. Find out the process by which ""_(11)^(24)Na can undergo radioactive decay:

1,1,2,2 -Tetrabromoethane whenheated withzincand alcoholgives :

1,1,2,2- tetrachloropropane was heated with zinc dust and the product was bubbled through ammonical AgNO_3. What is the weight of precipitate obtained?

1,1,2,2-tetra bromo ethane on heating with Zn powder in alcohol finally gives:

1.12 litre dry chlorine gas at STP was passed over a heated metal when 5.56 g of chloride of the metal was formed. What is the equivalent weight of the metal ?

11.1g. Of CaCl_(2) is present in 100 ml of the aqueous solution. The chloride ion concentration is

1.1 mole of A are mixed with 2.2 mole of Band the mixture is then kept In one litre flask till the equiliberium is attained A + 2B ⇌ 2C + D. At the equiliberium, 0.2 mole of C are formed. The equiliberium constant of the rection is :

1.1 mole of A are mixed with 2.2 mole of B and the mixture is then kept in a 1 L vessel till the equilibrium :A+2B hArr 2C+Dis reached.At equilibrium 0.2 moles of C are formed.The equilibrium constant for the reaction is :

11 g ,3 g

1,1-dichloroethane on boiling with KOH(aq.) yields :

1,1 - dichlorocyclohexane on alkaline hydrolysis gives

10mL of hydrogen contains 2xx10^(3) molecules of hydrogen at certain pressure and temperature. Calculate the number of molecules of oxygen whose volume is 200mL at the same temperature and pressure.

10mL of hydrogen combine with 5 mL of oxygen to yield water. When 200 mL of hydrogen at NTP are passed over heated CuO, the CuO loses 0.144 g of its mass. Do these resutls correspond to the law of constant proportions?

10ml of conc. H_(2)SO_(4) (18 molar) is diluted to 1 litre. The approximate strength of dilute acid could be

1.0M solution of a weak base, BOH is only 0.5% ionized. If 2mL 1 M solution of BOH is mixed with 30mL water, the degree of dissociation of the base in the resulting solution and H^(+) ion concentration of the solution will be respectivley.

10g solution of CuSO_4 is electrolyzed using 0.01F of electricity. Calculate : Equivalents of acid or alkali in the solution.

10g of hydrofluoric acid gas occupies 5.6 litre of volume at NTP. If the empirical of the gas is HF, then its molecular formula will be: (At. Mass of F=19)

10g of a radioactive substance is reduced to 1.25 g after 15 days. Its 1kg mass will reduce to 500g in

10g of a mixture of hexane and ethanol are reacted with Na to give 200mL of hydrogen at 27^(@)C and 760mmHg pressure. What is the percentage of ethanol in the mixture

10g hydrogen and 64 g oxygen were filled in a steel vessel and exploded, Amoung of water produced in this reaction will be

10g farily concentrated solution of CuSO_(4), is electrolysed by passing 10 ampere current for 1.5 minutes calculate. (a) The weight of resulting solution (b) The number of equivalents of acid or alkalli produced in solution (Cu=63.5)

10cm^(3) of 0.1N monobasic acid requires 15cm^(3) of sodium hydroxide solution whose normality is

10cm^(3) of 0.1 N monobasic acid requires 15cm^(3) of sodium hydroxide solution whose normality is

108Ã·7.2=14.583. The correct answer to this problem in proper number of significant digits is

10800C of electricity past through the electrolyte deposited 2.977 g of metal with atomic mass106.4 g mol^(-1). Find the charge on the metal cations.

10800 C of electricitythrough the electrolyte deposited 2.977 g of metal with atomic mass 106.4 g mol^(-1). Find the charge on the metal cations.

10800 C of electricity passed through an electrolyte deposited 2.977 g of metal with atomic mass 106.4 " g mol"^(-1) The charge on the metal cation is :

10800 C of electricity on passing through the electrolyte solution deposited 2.977g of metal with atomic mass 106.4 g mol^(-1) the charge on the metal cation is :

10.6 g of a substance of molecular weight 106 was dissolved in 100 ml 10 ml of this solution was pipetted out into a 1000 ml flask and made up to the mark with distilled water. The molarity of the resulting solution is

1.05 g of a lead ore containing impurity of Ag was dissolved in quantity of HNO_(3) and the volume was made 350 mL . A Ag electrode was dipped in the solution and E_(cell) of Pt(H_(2))|H^(+) (1 M)||Ag^(+)|Ag was 0.503 V at 298 K. calculate % of lead in the ore. E_(Ag^(+)//Ag)^(@)=0.80 V

1^(0),2^(0),3^(0) - amines can be distinguishedby using1) H_(2) O "" (2) R-X (3) HCl "" (4)(CH_(3)CO)_(2)O

10.1g of a volatile liquid occupies a volume of 4 litres when vaporised at 100^(@)C and 70 cm pressure. What would be the osmotic pressure of a 2% (grams per 100 "cc") solution of this substance at 0^(@)C?

100mL of a solution containning 5 g of NaOH is mixed with 200 mL of M/5 NaOH solution. Calculate the molarity of the resuliting solution.

100ml of 0.01 M solution of NaOH is diluted to 1dm^(3). What is the pH of the diluted solution

1.00g of a non-electrolyte solute dissolved in 50g of benzene lowered the freezing point of benzene by 0.40K. Freezing point depression constant of benzene is 5.12K g//mol. Find the molar mass of solute. .

1.00g of a non-electrolyte solute dissolved in 50g of benzene lowered by 0.40K. The freezing point depression constant of benzene is 5.12K kg//mol. Find the molar mass of solute.

100cm^(3) of an aqueous solution of BaCIU_(2)2H_(2)O is found to contain 6.022xx10^(22)CI^(-1)ilos. Calculate the molarity of the solution.

1000g of 1m aqueous solution of sucrose is cooled and maintained at -3.534^(@)C. Find how much ice will separate out. K_(f)(H_(2)O)=1.86K*kg*mol^(-1)

1000 g of 1 m sucrose solution in water is cooled to -3.354^(@)C. What mass of ice would separated out at this temperature ? K_(f) for H_(2)O= 1.86" K mol"^(-1)kg.

1000 g aqueous solution of CaCO_3contains 10 g calcium carbonate. Hardness of the solution is:

1000g of 1m aqueous solution of sucrose is cooled and maintained at -3.534^(@)C. Find how much ice will separate out. K_(f)(H_(2)O)=1.86Kkgmol^(-1)