94420 + Interview Questions in Chemistry in Class 12 Page 622 InterviewSolution

31051.	The decomposition of PH_(3) on tungsten at low pressure is a first order reaction. It is because the
Answer» rate is independent of SURFACE coverage rate of decomposition is very low rate is proportional to the surface coverage rate is inversely proportional to the surface coverage SOLUTION :The decomposition of `PH_3`on tungsten at low pressure is a FIRST order REACTION because rate is proportional to the surface cverage.

Discussion

31052.	The decomposition of ozone is believed to occur by the mechanism : O+ O_(3) rarr O_(2) ,(slow) When the concentration of O_(2) is increased, then the rate
Answer» increases decreases remains same cannot be PREDICTED ANSWER :B

Discussion

31053.	The decomposition of organic compounds, in the presence of oxygen and without the development of odoriferous ssubstances, is called
Answer» DECAY `N_(2)`-fixation nitrification denitrification Solution :Decomposition of organic compounds in the presence of oxygen is generally CALLED decay. The remaining THREE reactions takes PLACE in the presence of bacteria.

Discussion

31054.	The decomposition of N_(@)O into N_(2) and O_(2) presence of gaseous argon follows second order kinetics with k=(5.0xx10^(11)"L mol"^(-1)s^(-1))e^((-41570K)/(T)) (K stands for Kelvin units). The energy of activation of the reaction is :
Answer» `5.0xx10^(11)J` 41570 J 5000 J `345612.98` J Answer :D

Discussion

31055.	The decomposition of organic compounds in the presence of oxygen and without formation of odoriferoussubstances, is called
Answer» DECAY `N_(2)` fixation Nitrification Denitrification Solution :N//A

Discussion

31056.	Thedecompositionof nitrogenpentoxide is givenas 2N_(2)O_(5) to 4NO_(2) + O_(2) . The rates of reaction are ([N_(2)O_(5)])/(Delta t ) =k_(1)[N_(2)O_(5)],(Delta[NO_(2)])/(Deltat) = k_(2)[N_(2)O_(5)] and (Delta [O_(2)])/(Delta t) = k_(3) [N_(2)O_(5)] Relatethe rateconstants k_(1) , k_(2) and k_(3) .
Answer» SOLUTION :The rate of the reaction is given as `-(1)/(2)(DELTA[N_(2)O_(5)])/(DELTAT)=+(1)/(4)(Delta[NO_(2)])/(Deltat)=+(1)/(1)(Delta[O_(2)])/(Deltat)` Substituting the given values of rate in the above expression, `(1)/(2)k_(1)[n_(2)O_(5)]=(1)/(4)k_(2)[N_(2)O_(5)]=(1)/(1)k_(3)[N_(2)O_(5)]` Therefore, the rate constants `k_(1),k_(2)` and `k_(3)` are related as, `2k_(1)=k_(2)=4k_(3)`.

Discussion

31057.	The decomposition of NH_(3) on platinum surface is zero order reaction. What would be the rates of production of N_(2) and H_(2) if k=2.5xx10^(-4)"mol L"^(-1)s^(-1)?
Answer» Solution :For zero order reaction, rate of reaction = rate constant (k) `2NH_(3) to N_(2)+3H_(2)` Rate of reaction `=(d[N_(2)])/(dt)` HENCE, rate of production of `N_(2)=2.5xx10^(-4)"mol"^(-1)s^(-1)` Again, Rte of reaction `=(1)/(3)(d[H_(2)])/(dt)` or `(d[H_(2)])/(dt)=3xx` rate of reaction `=3xx2.5xx10^(-4)"mol L"^(-1)s^(-1)=7.5xx10^(-4)"mol L"^(-1)s^(-1)`

Discussion

31058.	The decomposition of NH_3 on the surface of finely divided platinum as catalyst
Answer» isalways a zero order RECTION is zero order at high concentration but 1st order at low concentrations is first order at low concentration but zero order at high concentration is ALWAYS a first order REACTION Solution :DECOMPOSITION of `NH_(3)` on the SURFACE of finely divided platinum is zero order at high concentration but first order at low concentration .

Discussion

31059.	The decomposition of NH_(3) on platinum surface is zero reaction. What are the rate of production of N_(2) and H_(2) is K=2.5xx10^(-4)"mol L"^(-1)s^(-1) ?
Answer» Solution :The reaction is `2NH_(3(g))overset("PT")rarr N_(2(g))+3H_(2(g))` Here `K=2.5xx10^(-4)"MOL L"^(-1)s^(-1)` The order of the reaction is zero i.e., Rate `=k ["Reactant"]^(@)` Rate `= 2.5xx10^(-4)xx1=2.5xx10^(-4)"mol L"^(-1)s^(-1)` `therefore (d)/(dt)[N_(2)]=(1)/(3)(d)/(dt)[H_(2)]` The rate of formation of `N_(2)=2.5xx10^(-4)"mol L"^(-1)s^(-1)` `therefore 2.5xx10^(-4)=(1)/(3)(d)/(dt)[H_(2)]` `therefore (d)/(dt)[H_(2)]=7.5xx10^(-4)` Therefore, rate of formation of `H_(2)` `= 7.5xx10^(-4)"mol L"^(-1)s^(-1)`

Discussion

31060.	The decomposition of NH_(3) on platinum surface is zero order reaction. What is the rate of production of N_(2)" if "K=2.5 times 10^(-4)" mol "L^(-1)" "S^(-1) ?
Answer» `2.5 times 10^(-4)" MOL "L^(-1)" "S^(-1)` `8.3 times 10^(-5)" mol "L^(-1)" "S^(-1)` `7.5 times 10^(-4)" mol "L^(-1)" "S^(-1)` `5 times 10^(-4)" mol "L^(-1)" "S^(-1)` Answer :A

Discussion

31061.	The decomposition of NH_(3) on platinum surface is zero order reaction. What are the rates of production of N_(2)and H_(2) if k=2.5xx10^(-4)"mol"^(-1)Ls^(-1)?
Answer» SOLUTION :`2NH_(3) to N_(2) +3H_(2)` Rate `= -(1)/(2) (d[NH_(3)])/(dt)= +(d[N_(2)])/(dt)= +(1)/(3)(d[H_(2)])/(dt)` For zero ORDER reaction, rate = k `therefore -(1)/(2) (d[NH_(3)])/(dt)=(d[N_(2)])/(dt)=(1)/(3)(d[H_(2)])/(dt)=2.5xx10^(-4)"mol L"^(-1)s^(-1)` `therefore ` Rate of production of `N_(2)=(d[N_(2)])/(dt)=2.5xx10^(-4)"mol L"^(-1)s^(-1)` Rate of production of `H_(2)=(d[H_(2)])/(dt)` `=3xx(2.5xx10^(-4)"mol L"^(-1)s^(-1))=7.5xx10^(-4)"mol L"^(-1)s^(-1)`.

Discussion

31062.	The decomposition of NH_(3) on platinum surface Is zero order reaction .What are the rates of production of N_(2) and H_(2) if k=2.5xx10^(-4) mol^(-1) L s^(-1)?
Answer» Solution :Decomposition of `NH_(3)` is as follows: `2NH_(3(G))toN_(2(g))+3H_(2(g))` `k=2.5xx10^(-4) mol L^(-1)s^(-1)` Reaction is of zero order Rate of reaction =`-(1)/(2)(d[NH_(3)])/(dt)=(d[N_(2)])/(dt)=(1)/(3)-(d[H_(2)])/(dt)` as the reaction is zero order Rate of formation of `N_(2)=(d[N_(2)]^(0))/(dt)=k` `2.5xx10^(-4)mol L^(-1)s^(-1)` Rate of formation of `H_(2)` `=k=(1)/(3) (d[H_(2)]^(0))/(dt)=2.5x10^(-4)=k` `therefore (d[H_(2)])/(dt)=3xx2.5xx10^(-4)`

Discussion

31063.	The decomposition of NH_(3) on platinum surface is zero order reaction what are the rates of production of N_(2) and H_(2) if k=2.5xx10^(-4)mol^(-1)Ls^(-1).
Answer» Solution :`2NH_(3(G))overset(PT)rarr N_(2(g))+3H_(2(g))` Rate `=-(1)/(2)(d[NH_(3)])/(DT)=(d[N_(2)])/(dtr)=(1)/(3)(d[N_(2)])/(dt)` However, it given that the reaction is of zero ORDER. Therefore `-(1)/(2)(d[NH_(3)])/(dt)=(d[N_(2)])/(dt)=(1)/(3)(d[H_(2)])/(dt)k` `= 2.5xx10^(-4)"mol L"^(-1)s^(-1)` The rate of production of `N_(2)` is `(d[N_(2)])/(dt)=2.5xx10^(-4)"mol L"^(-1)s^(-1)` The rate of production of `H_(2)` is `(d[N_(2)])/(dt)=3xx2.5xx10^(-4)"mol L"^(-1)s^(-1)` `= 7.5xx10^(-4)"mol L"^(-1)s^(-1)`.

Discussion

31064.	The decomposition of NH_(3) on platinum surface, 2 NH_(3)(g)overset(Pt)toN_(2)(g)+3H_(2)(g),is zero order with k=2*5xx10^(-4)molL^(-1)s^(-1). What are the rates of production of N_(2) and H_(2) ?
Answer» Solution :`2 NH_(3)toN_(2)+3 H_(2)," Rate"=-(1)/(2)(d[NH_(3)])/(dt)=+(d[N_(2)])/(dt)=+(1)/(3)(d[H_(2)])/(dt)` For zero ORDER reaction, rate `=k:.-(1)/(2)(d[NH_(3)])/(dt)=(d[N_(2)])/(dt)=(1)/(3)(d[H_(2)])/(dt)=25xx10^(-4)molL^(-1)s^(-1)` `:." Rate of PRODUCTION of "N_(2)=(d[N_(2)])/(dt)=25xx10^(-4)molL^(-1)s^(-1)` Rate of production of `H_(2)=(d[H_(2)])/(dt)=3xx(25xx10^(-4)molL^(-1)s^(-1))=75xx10^(-4)molL^(-1)s^(-1)`.

Discussion

31065.	The decomposition of NH_3 on platinum surface is zero· order with rate constant k = 2.5 xx 10^(-4) mol L^(-1) s^(-1). The rate of production of H_2 will be
Answer» `2.5 xx 10^(-4) mol L^(-1) s^(-1)` `0.83 xx 10^(-4) mol L^(-1) s^(-1)` `7.5 xx 10^(-4) mol L^(-1) s^(-1)` `5.0 xx 10^(-4) mol L^(-1) s^(-1)` Solution :`2NH_3 overset(Pt)to N_2+3H_2` `"RATE"= 1/2(d[NH_3])/(dt)=(d[N_2])/(dt)= 1/3(d[H_2])/(dt)` `=1/3 (d[H_2])/(dt)=k = 2.5 xx 10^(-4)mol L^(-1)s^(-1)` Rate of production of `H_2`. `:. (d[H_2])/(dt) = 3 xx 2.5 xx 10^(-4)` `=7.5 xx 10^(-4)mol L^(-1)s^(-1)`

Discussion

31066.	The decomposition of NH, on platinum surface is zero order reaction. If rate constant (k) is 4xx10^(-3) Ms^(-1), how long will it take to reduce the initial concentration of NH_(3) from 0.1 M to 0.064 M.
Answer» SOLUTION :`t=([R]0-[R]t)/(K)=([0.1-0.064])/(4xx10^(-3))=9 SEC`

Discussion

31067.	The decomposition of NH_3 on platinum surface is a zero order reaction. What would be the rate of production of N_2 and H_2 if k=2.5xx10^(-4) "mol L"^(-1) s^(-1) ?
Answer» SOLUTION :`2NH_3 to N_2+ 3H_2` `-1/2(d[NH_3])/(dt)=(d[NH_2])/(dt)+1/3(d[H_2])/(dt)` `(d[NH_3])/(dt)`=rate `=KXX[NH_3]^0` `=2.5xx10^(-4) "mol L"^(-1) "SEC"^(-1)` `(d[N_2])/(dt)=-1/2 (d[NH_3])/(dt)` `=1/2xx2.5xx10^(-4)"mol L"^(-1) "sec"^(-1)` `d[H_2]=-3/2 (d[NH_3])/(dt)=3/2xx2.5xx10^(-4)` `=3.75xx10^(-44) "mol L"^(-1) "sec"^(-1)` Rate=`-(d[NH_3])/(dt)=kxx[NH_3]^0` `=2.5xx10^(-4)"mol L"^(-1) "sec"^(-1)` Rate of production of `N_2=2.5xx10^(-4) "mol L"^(-1) "sec"^(-1)`

Discussion

31068.	The decomposition of N_(2)O_(5)(g) is a first order reaction with a rate constant of 5xx10^(-4)s^(-1) at 45^(@)C. i.e., 2N_(2)O_(5)(g) to 4NO_(2)(g)+O_(2)(g). If initial concentrationof N_(2)O_(5) is 0.25M, calculate its concentration after 2 minutes. Also calculate the half-life for decomposition of N_(2)O_(5)(g).
Answer» Solution :`K=5xx10^(-4)s^(-1), [R]_(0)=0.25 M, t=2xx60=120s` Use the relation, `k=(2.303)/(t)"log"([R]_(0))/([R])` Substituting the values, we get `5xx10^(-4)s^(-1)=(2.303)/(120s)"log"([R]_(0))/([R])` `"log"([R]_(0))/([R])=(5xx10^(-4)sxx120s)/(2.303)=0.02605 or ([R]_(0))/([R])=1.061` Substitutingthe value of `[R]_(0)`, we have `(0.25)/([R])=1.061 or [R]=(0.25)/(1.061)=0.23M` Half-life can be calcualted USING the relation: `t_(1//2)=(0.693)/(k)=(0.693)/(5xx10^(-4)s^(-1))=1386s`

Discussion

31069.	The decomposition of N_(2)O_(5)(g) is a first order reaction with a rate constant of 5xx10^(-4)s^(-1) at 45^(@)C. i.e., 2N_(2)O_(5)(g) to 4NO_(2)(g)+O_(2)(g). If initial concentrationof N_(2)O_(5) is 0.25M, calculate its concentration after 2 min. Also calculate half-life for decomposition of N_(2)O_(5) (g).
Answer» SOLUTION :`k=5xx10^(-4)s^(-1), [R]_(0)=0.25 M, t=2 "min"=120S` USING `k=(2.303)/(t)"log"([R]_(0))/([R])" or log"([R]_(0))/([R])=(kt)/(2.303)` Substituting the values, we GET `"log"(0.25)/([R])=(5xx10^(-4)xx120)/(2.303)=0.02605 or (0.25)/([R])=` ANTILOG 0.02605 = 1.061 or`[R]=(0.25)/(1.061)=0.23M` `t_(1//2)=(0.693)/(k)=(0.693)/(5xx10^(-4)) or t_(1//2)=1386`

Discussion

31070.	The decomposition of N_(2) O_(5) by 2N_(2) O_(5) to 4NO_(2) + O_(2) follows first order kinetics. Select the incorrect statement.
Answer» The REACTION is bimolecular The reaction is UNIMOLECULAR `t_(1//2)ooa^@` None of the above Answer :C

Discussion

31071.	The decompositionof N_2O_5 occurs as, 2N_2O_5 to 4NO_2 + O_2, and follows I order kinetics, The true statement is
Answer» `K=([A]_o-[A]_t)/t` the reaction is unimolecular `t_(1//2) prop [A]_o^o` `t_(1//2) prop [A]_o^2` Solution :For 1 order reaction half LIFE is INDEPENDENT of CONCENTRATION .

Discussion

31072.	The decomposition of N_(2)O_(5) in CCl_(4) solution follows the first order rate law. The concentrations of N_(2)O_(5) measured at different intervals are given below : {:("Time in seconds (t)",,,0,,,80,,,160,,,410,,,600,,,1130,,,1720),(["N"_(2)"O"_(5)]"mol"//"L",,,5.5,,,5.0,,,4.8,,,4.0,,,3.4,,,2.4,,,1.6):} Calculate the rate constant at t = 410 s and t = 1130 s. What do these results show ?
Answer» SOLUTION :According to FIRST ORDER rate LAW, `K=(2.303)/(t)log""(a)/(a-x)=(2.303)/(t)log""(["N"_(2)"O"_(5)]_(0))/(["N"_(2)"O"_(5)]_(t))` `{:("At "t=410" s"",",,,k=(2.303)/(410s)log""(5.5)/(4.0)=7.768xx10^(-4)s^(-1)),("At "t=1130"s"",",,,k=(2.303)/(1130s)log""(5.5)/(2.4)=7.341xx10^(-4)s^(-1)):}` These results show that the rate constant is nearly constantat differenttimes.

Discussion

31073.	The decomposition of N_(2)O_(5) in CCl_(4) solution at 318 K has been studied by monitoring the concentration of N_(2)O_(5) in the solution. Initially the concentration of N_(2)O_(5) is 233 M and after 184 minutes, it is reduced to 208 M. The reaction takes place according tothe equation : 2N_(2)O_(5)to4NO_(2)+O_(2) Calculate the average rate of this reaction in terms of hours, minutes and seconds. What is the rate of production of NO_(2) during this period ?
Answer» Solution :Average Rate `=-(1)/(2)(Delta[N_(2)O_(5)])/(Deltat)=-(1)/(2)((208-233)MOLL^(-1))/(184min)=679xx10^(-4)molL^(-1)min^(-1)` `=(679xx10^(-4)molL^(-1))/(min)xx(1min)/(60s)=1.13xx10^(-5)molL^(-1)s^(-1)` `=(679xx10^(-4)molL^(-1))/(min)xx(60min)/(1HR)=407xx10^(-2)molL^(-1)hr^(-1)` Rate `=(1)/(4)(Delta[NO_(2)])/(Deltat)=-(1)/(2)(Delta[N_(2)O_(5)])/(Deltat)=679xx10^(-4)molL^(-1)min^(-1)""("calculatedabove")` `:." Rate of production of "NO_(2),(Delta[NO_(2)])/(Deltat)=4xx679xx10^(-4)molL^(-1)min^(-1)=272xx10^(-3)molL^(-1)min^(-1)`

Discussion

31074.	The decomposition of N_2O_5 occurs as, 2N_2O_5 to 4NO_2 + O_2 and follows first order kinetics, hence:
Answer» the reaction is bimolecular the reaction is unimolecular `t_1/2 prop a^@` unit of `K=(MOL)/L "sec"^(-1)` ANSWER :C

Discussion

31075.	The decomposition of N_(2)O_(5) in CCl_(4)at 318K has been studied by monitoring the concentration of N_(2)O_(5) in the solution.Initially the concentration of N_(2)O_(5) is 2.33 mol L^(1) and after 184 minutes ,it is reduced of 2.08 mol L^(-1) .The reaction take place according to the equation 2N_(2)O_(5(g))to4NO_(2(g))+O_(2(g)) Calculate the average rate of this reaction in terms of hours,minutes and seconds.What is the rate of production of N_(0)2 during this period?
Answer» Solution :The balance equation of reactants are as under: `2N_(2)O_(5(g))to4NO_(2(g))+O_(2(g))` Average Rate=`-(1)/(2){(Delta[N_(2)O_(5)])/(DELTAT)}` `(1)/(4)((Delta[NO_(2)])/(Deltat))` `(Delta[O_(2)])/(Deltat)` Initial t=0,the concentration of `N_(2)O_(5)=2.33 ml L^(-1)` after 184 minutes ,the concentration of `N_(2)O_(5)=2.08 MOL L^(-1)` So, `Deltat`=(184-0.0) minute=184 minute `Delta[R]=[R_(2)]-[R_(1)]` `=-0.25 mol L^(-1)` `therefore` Avereage rate =`-(1)/(2)(Delta[N_(2)O_(5)])/(Deltat)` `-(1)/(2)(-0.25 mol L^(1))/(184 min)` `r_(av)` (in second)=`(1)/(2)(Delta[R])/(Deltat("in second"))` `(-0.25)/(2xx(184xx60)s)` `=1.1322xx10^(-5) mol L^(-1)S^(-1)` `r_(av)`(in HOUR)=`-(1)/(2) (Delta[R])/(Deltat ("in hour"))` `=-(-0.25 mol L^(-1))/(2xx(184+60)h)` `(+0.25xx60)/(2xx184) mol L^(-1) h^(-1)`

Discussion

31076.	The decomposition of N_(2)O_(5) occurs as, 2N_(2)O_(5) rarr4NO_(2)+O_(2) and follows I order kinetics, hence:
Answer» The REACTION is UNIMOLECULAR The reaction is bimolecular `T_(1//2) PROP a^(0)` None of these ANSWER :c

Discussion

31077.	The decomposition of N_(2)O_(5) in (C)Cl_(4) at 318 K is studied by monitoring the concentration of N_(2)O_(5) in the solution. Initially the concentration of N_(2)O_(5) is 2.4 mol L^(-1). What is the rate of production of NO_(2) during this period in mol L^(-1)min^(-1) ?
Answer» `4 XX 10^(-3)` `2 xx 10^(-3)` `1 xx 10^(-3)` `2 xx 10^(-4)` SOLUTION :a) `2N_(2)O_(5) to 4NO_(2) + O_(2)` `1//2 xx "Rate of disappearance of" N_(2)O_(5)` `=1/4 xx "Rate of production of" NO_(2)` Rate of production of `NO_(2)` = `4/2` Rate of disappearance of `N_(2)O_(5)` `(2.4 -2.0)/(200) = 0.4/100 = 4 xx 10^(-3) MOL L^(-1)min^(-1)`

Discussion

31078.	The decomposition of N_(2)O_(5) in carbon tetrachloride solution was studied N_(2)O_(5)("solution")to2NO_(2)("solution")+(1)/(2)O_(2)(g) The reaction has been found to be first order and the rate constant is found to be 6.2xx10^(-4)s^(-1). Calculate the rate of reaction when (a)[N_(2)O_(5)]=1.25" mol L"^(-1)" and "(b)[N_(2)O_(5)]=0.25" mol L"^(-1). (c) What concentration of N_(2)O_(5) would give a rate of 2.4xx10^(-3)" mol L"^(-1)s^(-1)?
Answer» Solution :(a) Rate `=k[N_(2)O_(5)]=(6.2xx10^(-4)s^(-1))(1.25" mol L"^(-1))=7.75xx10^(-4)" mol L"^(-1)s^(-1)` (B) Rate `=(6.2xx10^(-4)s^(-1))(0.25" mol L"^(-1))=1.55xx10^(-4)" mol L"^(-1)s^(-1)` (c) `2.4xx10^(-3)" mol L"^(-1)s^(-1)=(6.2xx10^(-4)s^(-1))[N_(2)O_(5)]" or "[N_(2)O_(5)]=3.87" mol L"^(-1).`

Discussion

31079.	The decomposition of N_(2)O_(5) in carbon tetrachloride was followed by measuring the volume of O_(2) gas evolved : 2NO_(2)O_(5)(C Cl_(4)) to 2N_(2)O_(4)(C Cl_(4))+O_(2)(g). The maximum volume of O_(2) gas obtained was 100 cm^(3). In 500 minutes, 90 cm^(3) of O_(2) were evolved. The first order rate constant (in min^(-1)) for the disappearance of N_(2)O_(5) is:
Answer» `(2.303)/(500)` `(2.303)/(500)log""(100)/(90)` `(2.303)/(500)log""(90)/(100)` `(100)/(10 XX 500)` Solution : `k=(1)/(t)In(a)/(a-x)=(2.303)/(500)`

Discussion

31080.	The decomposition of N_(2)O_(5) in C Cl_(4) at 318 K is studied by monitoring the concentration of N_(2)O_(5) in the solution. Initially, the concentration of N_(2)O_(5) is 2.4" mol L"^(-1) and after 200 minutes, it is reduced to 2.00" mol L"^(-1). What is the rate of production of NO_(2) during this period in mol L"^(-1)"min"^(-1) ?
Answer» `4xx10^(-3)` `2xx10^(-3)` `1xx10^(-3)` `2xx10^(-4)` SOLUTION :`2N_(2)O_(5) to NO_2) + O_(2)` Rate of reaction `= -(1)/(2) (d[N_(2)O_(5)])/(dt) = + (1)/(4)(d[NO_(2)])/(dt)"" …(i)` Rate of DISAPPERANCE of `N_(2)O_(5) ((-d[N_(2)O_(5)])/(dt))` ` = ((24 - 20))/(20 min) mol L^(-1)` `=(0*4)/(200) mol L^(-1) min^(-1)` ` = 2 xx 10^(-3) mol L^(-1) min^(-1)` From EQU. (i), Rate of production of `NO_(2)(+(d[NO_(2)])/(dt))` `= -4 xx(1)/(2)(d[N_(2)O_(5)])/(dt)` `=-2 xx(-2 xx 10^(-3)) mol L^(-1) min^(-1)` `=4 xx 10^(-3) mol L^(-1) min^(-1)`

Discussion

31081.	The decomposition of N_(2)O_(5) according to the equation2N_(2)O_(5)(g)rarr4NO_(2)(g)+O_(2)(g)is a first order reaction. After 30min, from the start of the decomposition in a closed vessel, total pressure developed is 284.5 mm Hg. On complete decomposition, total pressure is 584.5mm Hg. Calculate the rate constant of reaction .
Answer» Solution :Given REACTION `2N_(2)O_(5)(g)rarr4NO_(2)(g)+O_(2)(g)` `""N_(2)O_(5)(g)rarr2NO_(2)(g)+(1)/(2)O_(2)(g)` `{:("Initial no.of moles:",""a,0,0),("No.of moles at TIME t:",(a-x),2x,x//2),("No. of moles after",,,),("COMPLETE decomposition",0,2a,a//2):}` `therefore` Total no.of moles after complete decomposition `=2a+(a)/(2)=(5)/(2)a` At a given volume and temperature , `pprop n` [ Assuming ideal behaviour of GAS mixture] According to the given data, `(5)/(2)a prop584.5mmHg""....[1]` and`(3)/(2)x prop284.5mmHg""....[2]` or, `thereforeaprop233.8mmHg and (3)/(2)xprop284.5-a` or, `(3)/(2)xprop284.5-233.8prop50.7"mmHg " thereforexprop33.8 mm HG` Therefore ,`(a-x)prop(233.8-33.8)"mmHg"` i.e., `(a-x)prop"mm Hg"` `thereforek=(2.303)/(t)log.(a)/(a-x)=(2.303)/(30)log.(233.8)/(200)` or,`k=5.21xx10^(-3)"min"^(-1)`

Discussion

31082.	The decomposition of N_(2)O_(5) according to the equation 2N_(2)O_(5) (g) rarr 4 NO_(2)(g) + O_(2) (g) is a first order reaction. After 30 min. from start of decomposition in a closed vessel the total pressure developed in found to be 284.5 mm Hg. On complete decomposition, the toal pressure is 584.5 mm Hg. Calculate the rate constant of the reaction.
Answer» SOLUTION :`k_(1) =2.605xx10^(-3)" MIN"^(-1)`

Discussion

31083.	The decomposition of N_(2)O_(5) according to following reaction is first order reaction : 2N_(2)O_(5)(g) rarr 4NO_(2)(g) + O_(2) (g) After 30 min. from start of the decomposition in a closed vessel, the total pressure developed is found to be 284.5 mm of Hg and on complete decomposition, the total pressure is 584.5 mm of Hg. Calculate the rate constant of the reaction.
Answer» <P> Solution :`2N_(2)O_(5)(g)rarr4NO_(2)(g)+O_(2)(g)`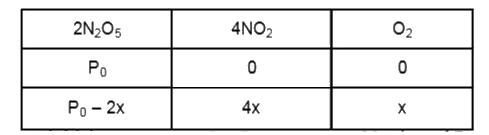 `P_(0):` initial pressure , LET `P_(t)` : pressure at 30 MIN and `P_(oo)` : pressure at the end of decompositon. `rArr " "P_(t) =P)(0)+3x` `rArr " "x=(1)/(3) (P_(t)-P_(0)) and P_(oo) =2P_(0)+(1)/(2)P_(0)=(5)/(2)P_(0)` `rArr" "P_(0)=(2)/(5) P_(oo)` For the first order kinetics `k_("eff")t=2.303 log_(10)""(A_(0))/(A)` `A_(0):` initial concentration , A: final concentration Now `" "(A_(0))/(A) =(P_(0))/(P_(0)-2x)=((1)/(5)P_(oo))/((1)/(5)P_(oo)-2(P_(t)-2//5P_(oo))/(3))` `rArr" "(A_(0))/(A) =(3)/(5)((P_(oo))/(P_(oo)-P_(t)))` `rArr" "k_("eff") =(1)/(30)xx2.303 log_(10)""(3)/(5) XX(584.5)/(584.5-284.5)` `=5.204xx10^(-3)" min"^(-1)` k for the reaction `=(5.204)/(2)xx10^(-3)=2.602xx10^(-3)" min"^(-1)`

Discussion

31084.	The decomposition of N_(2)O_(4) to NO_(2) is carried out at 280K in chloroform. When equilibrium has been estabilished, 0.2 mol of N_(2)O_(4) and 2xx10^(-3)mol of NO_(2) are present in 2 litre solution. The equlibrium constant for reaction N_(2)O_(4)hArr 2NO_(2) is
Answer» `1xx10^(-2)` `2xx10^(-3)` `1xx10^(-5)` `2xx10^(-5)` Solution :`K=([NO_(2)]^(2))/([N_(2)O_(4)])=([2xx(10)/(2)^(-3)]^(2))/([(2)/(2)])=(10^(-6))/(10^(-1))=10^(-5).`

Discussion

31085.	The decomposition of N_(2)O_(4) to NO_(2) is carried out at 280^(@)C in chloroform. When equilibrium is reached, 0.2 mol of N_(2)O_(4) and 2xx10^(-3) mol of NO_(2) are present in 2 litre solution. The equilibrium constant for the reaction, N_(2)O_(4)iff2NO_(2) is
Answer» `1xx10^(-3)` `2xx10^(-3)` `1xx10^(-5)` `2xx10^(-5)` Solution :`K=([NO_(2)]^(2))/([N_(2)O_(4)])=((2xx10^(-3)//2)^(2))/((0.2//2))=(10^(-6))/(10^(-1))=10^(-5)`

Discussion

31086.	The decomposition of N_2O into N_2and O in the presence of gaseous argon follows second-order kinetics, withk = (5.0 xx 10^11 L "mol"^(-1) s^(-1) ) e^(-2900 k//T) What is the energy of activation of this reaction?
Answer» SOLUTION :COMPARE the GIVEN EQUATION with Arrhenius.s equation.

Discussion

31087.	The decomposition of N_2O_4 to NO_2 is carried out at 280 K in chloroform.When equiliberium has been established,0.2 mole of N_2O_4 and 2 xx 10^(-3) mole of NO_2 are present in a 2 litre solution. THE equiliberium constant for the reaction, N_2O_4 ⇌ 2NO_2 is :
Answer» `1 xx 10^(-2)` `1 xx 10^(-3)` `1 xx 10^(-5)` `2 xx 10^(-5)` Answer :C

Discussion

31088.	The decomposition of N_(2)O in carbon tetrachloride was followed bymesuring the volume of O_(2) gas evolved :2N_(2)O_(5)("CCL"_(4))to2N_(2)O_(4)("CC"L_(4))+O_(2)(g) . The maximum volume of O_(2) gas obtained was 100 cm^(3). In 500 minutes, 90 cm of O_(2) were evolved. The first order rate constant (in min^(-1) for the dissaperance of N_(2)O is :
Answer» `(2.303)/(500)` `(2.303)/(500)"LOG"(100)/(90)` `(2.303)/(500)"log"(90)/(100)` `(100)/(10xx500)` ANSWER :A

Discussion

31089.	Thedecompositionof N_(2) O_(5)is representedby theequation 2N_(2)O_(5(g)) to 4NO_(2(g))+ O_(2(g)) (a ) Howis therate offormationof NO_(2)relatedto the rate offormationof O_(2)? (b ) Howis therateof formationof O_(2) relatedto therate ofconsumption of N_(2)O_(s)?
Answer» Solution : Given : `2N_(2)O_(5(g)) to 4NO_(2(g)) + O_(2(g))` (a)Rateof formationof `O_(2)` at time`t= (d[O_(2)])/(DT)` Theyare relatedto eachotherthrough RATE of reaction `:. ` Rateof reaction`=(1)/(4) (d[NO_(2)])/(dt)= (d[O_(2)])/(dt)` ( b) Rate ofconsumptionof `N_(2) O_(5)` at time `t= - (d[N_(2)O_(5)])/(dt)` Rateof reaction `=- (1)/(2)(d[N_(2)O_(5)])/(dt) =(d[O_(2)])/(dt)` INGENERAL Rate ofreaction`= -(1)/(2) (d[N_(2)O_(5)])/(dt)= (1)/(4) (d[NO_(2)])/(dt)= (d[O_(2)])/(dt)`

Discussion

31090.	The decomposition of KCIO_3 to KCI AND O_2 on heating is an example of :
Answer» INTERMOLECULAR REDOX change Intramolecular redox change combination change None of the above Answer :B

Discussion

31091.	The decomposition of hydrogen peroxide in the presence of colloidal platinum is a/an
Answer» POSITIVE catalysis negative catalysis auto-catalysis induced catalysis Answer :A

Discussion

31092.	The decomposition of hydrogen peroxide can be slowed down by the addition of a small amount ofacetanilide. The latter acts as
Answer» Inhibitor Promoter Moderator Poison Answer :A

Discussion

31093.	The decomposition of hydrocarbon follows the equation k=(4.5xx10^(11)s^(-1))e^(-28000K//T) Calculate E_(a)
Answer» Solution :K=`4.5xx10^(11)s^(-1)e^(-28000 K//T)` Calculation of `E_(a)`,here ,k indicate TEMPERATURE in kelvin. According to Arrhenius k=`Ae^(-E_(a)//RT)` …….(b) `therefore` Compairing (a) and (b)so,In (a)`4.5xx10^(11)` is K of (b). In (a),`e^(-28000K//T)`=In (b),`e^(-E_(a)//RT)` means,`-(E_(a))/(RT)=-(28000K)/(T)` `therefore E_(a)=28000 KxxR`

Discussion

31094.	The decomposition of hydrocarbon follows the equation k=(4.5xx10^(11)s^(-1))e^(-28000K//T). Calculate E_(a).
Answer» Solution :Given that `k=(4.5xx10^(11)s^(-1))e^(-28000K//T)` According to Arrhenius EQUATION, `k=Ae^(-E_(a)//RT)` EQUATING SIMILAR terms `-(E_(a))/(RT)=(28000K)/(T)` or `E_(a)=28000 K xx R=28000 K xx 8.314 JK^(-1)"mol"^(-1)=232.79"KJ mol"^(-1)`.

Discussion

31095.	The decomposition of hydrogen peroxide can be slowed by addition of a small amount of acetamide. The later acts as a:
Answer» Detainer Stopper Promoter Inhibitor Answer :D

Discussion

31096.	The decomposition of H_2O_2 rate is decreased by ................
Answer» SOLUTION :ETHANOL ( or ) GLYCEROL ,NEGATIVECATALYST

Discussion

31097.	The decomposition of hydrocarbonfollows the equation k=(4.5xx10^(11)s^(-1))e^(-28000K//T) Calculate E_(a).
Answer» SOLUTION :`K=(4.5xx10^11 s^(-1)) e^(-28000k//T)` COMPARING the equation with Arrhenius equation, `K=Ae^(-Ea//RT)` `-E_a/R=-28000` K `E_a=28000xx8.314` `=232192 J "MOL"^(-1)`

Discussion

31098.	The decomposition of H_2O_2 may be checked by adding a small quantity of phosphoric acid. This is an example of :
Answer» Neutralization Negative catalysis Positive catalysis Catalytic poisoning Answer :B

Discussion

31099.	The decomposition of H_(2)O_(2) may be checked by adding a small quantity of phosphoric acid. This is an example of
Answer» autocatalysis negative catalysis positive catalysis catalytic promotion. Solution :`H_(3)PO_(4)`acts as negative CATALYST for decomposition of `H_(2)O_(2)`

Discussion

31100.	The decomposition of ethane into ethene and hydrogen involves 5 different steps, having rate constants K_(1), K_(2), K_(3), K_(4) and K_(5). The rate law is given by: (-d[C_(2)H_(6)])/(dt)=((K_(1)K_(3)K_(4))/(K_(5)))^((1)/(2))[C_(2)H_(6)] if E_(a_(1))(10 kJ //mol), E_(a_(3))(5kJ//mol),E_(a_(4))(3kJ//mol)) and E_(a_(5))(0) are the energies of activation associated with 1^(st), 3^(rd), 4^(th) and 5^(th) steps respectively, find the overall energy of activation for ethane decomposition.
Answer» ANSWER :`9kJ//mol`

Discussion

Explore topic-wise InterviewSolutions in .

The decomposition of PH_(3) on tungsten at low pressure is a first order reaction. It is because the

The decomposition of ozone is believed to occur by the mechanism : O+ O_(3) rarr O_(2) ,(slow) When the concentration of O_(2) is increased, then the rate

The decomposition of organic compounds, in the presence of oxygen and without the development of odoriferous ssubstances, is called

The decomposition of N_(@)O into N_(2) and O_(2) presence of gaseous argon follows second order kinetics with k=(5.0xx10^(11)"L mol"^(-1)s^(-1))e^((-41570K)/(T)) (K stands for Kelvin units). The energy of activation of the reaction is :

The decomposition of organic compounds in the presence of oxygen and without formation of odoriferoussubstances, is called

Thedecompositionof nitrogenpentoxide is givenas 2N_(2)O_(5) to 4NO_(2) + O_(2) . The rates of reaction are ([N_(2)O_(5)])/(Delta t ) =k_(1)[N_(2)O_(5)],(Delta[NO_(2)])/(Deltat) = k_(2)[N_(2)O_(5)] and (Delta [O_(2)])/(Delta t) = k_(3) [N_(2)O_(5)] Relatethe rateconstants k_(1) , k_(2) and k_(3) .

The decomposition of NH_(3) on platinum surface is zero order reaction. What would be the rates of production of N_(2) and H_(2) if k=2.5xx10^(-4)"mol L"^(-1)s^(-1)?

The decomposition of NH_3 on the surface of finely divided platinum as catalyst

The decomposition of NH_(3) on platinum surface is zero reaction. What are the rate of production of N_(2) and H_(2) is K=2.5xx10^(-4)"mol L"^(-1)s^(-1) ?

The decomposition of NH_(3) on platinum surface is zero order reaction. What is the rate of production of N_(2)" if "K=2.5 times 10^(-4)" mol "L^(-1)" "S^(-1) ?

The decomposition of NH_(3) on platinum surface is zero order reaction. What are the rates of production of N_(2)and H_(2) if k=2.5xx10^(-4)"mol"^(-1)Ls^(-1)?

The decomposition of NH_(3) on platinum surface Is zero order reaction .What are the rates of production of N_(2) and H_(2) if k=2.5xx10^(-4) mol^(-1) L s^(-1)?

The decomposition of NH_(3) on platinum surface is zero order reaction what are the rates of production of N_(2) and H_(2) if k=2.5xx10^(-4)mol^(-1)Ls^(-1).

The decomposition of NH_(3) on platinum surface, 2 NH_(3)(g)overset(Pt)toN_(2)(g)+3H_(2)(g),is zero order with k=2*5xx10^(-4)molL^(-1)s^(-1). What are the rates of production of N_(2) and H_(2) ?

The decomposition of NH_3 on platinum surface is zero· order with rate constant k = 2.5 xx 10^(-4) mol L^(-1) s^(-1). The rate of production of H_2 will be

The decomposition of NH, on platinum surface is zero order reaction. If rate constant (k) is 4xx10^(-3) Ms^(-1), how long will it take to reduce the initial concentration of NH_(3) from 0.1 M to 0.064 M.

The decomposition of NH_3 on platinum surface is a zero order reaction. What would be the rate of production of N_2 and H_2 if k=2.5xx10^(-4) "mol L"^(-1) s^(-1) ?

The decomposition of N_(2) O_(5) by 2N_(2) O_(5) to 4NO_(2) + O_(2) follows first order kinetics. Select the incorrect statement.

The decompositionof N_2O_5 occurs as, 2N_2O_5 to 4NO_2 + O_2, and follows I order kinetics, The true statement is

The decomposition of N_2O_5 occurs as, 2N_2O_5 to 4NO_2 + O_2 and follows first order kinetics, hence:

The decomposition of N_(2)O_(5) occurs as, 2N_(2)O_(5) rarr4NO_(2)+O_(2) and follows I order kinetics, hence:

The decomposition of N_(2)O_(5) in (C)Cl_(4) at 318 K is studied by monitoring the concentration of N_(2)O_(5) in the solution. Initially the concentration of N_(2)O_(5) is 2.4 mol L^(-1). What is the rate of production of NO_(2) during this period in mol L^(-1)min^(-1) ?

The decomposition of N_(2)O_(4) to NO_(2) is carried out at 280K in chloroform. When equilibrium has been estabilished, 0.2 mol of N_(2)O_(4) and 2xx10^(-3)mol of NO_(2) are present in 2 litre solution. The equlibrium constant for reaction N_(2)O_(4)hArr 2NO_(2) is

The decomposition of N_(2)O_(4) to NO_(2) is carried out at 280^(@)C in chloroform. When equilibrium is reached, 0.2 mol of N_(2)O_(4) and 2xx10^(-3) mol of NO_(2) are present in 2 litre solution. The equilibrium constant for the reaction, N_(2)O_(4)iff2NO_(2) is

The decomposition of N_2O into N_2and O in the presence of gaseous argon follows second-order kinetics, withk = (5.0 xx 10^11 L "mol"^(-1) s^(-1) ) e^(-2900 k//T) What is the energy of activation of this reaction?

The decomposition of N_2O_4 to NO_2 is carried out at 280 K in chloroform.When equiliberium has been established,0.2 mole of N_2O_4 and 2 xx 10^(-3) mole of NO_2 are present in a 2 litre solution. THE equiliberium constant for the reaction, N_2O_4 ⇌ 2NO_2 is :

Thedecompositionof N_(2) O_(5)is representedby theequation 2N_(2)O_(5(g)) to 4NO_(2(g))+ O_(2(g)) (a ) Howis therate offormationof NO_(2)relatedto the rate offormationof O_(2)? (b ) Howis therateof formationof O_(2) relatedto therate ofconsumption of N_(2)O_(s)?

The decomposition of KCIO_3 to KCI AND O_2 on heating is an example of :

The decomposition of hydrogen peroxide in the presence of colloidal platinum is a/an

The decomposition of hydrogen peroxide can be slowed down by the addition of a small amount ofacetanilide. The latter acts as

The decomposition of hydrocarbon follows the equation k=(4.5xx10^(11)s^(-1))e^(-28000K//T) Calculate E_(a)

The decomposition of hydrocarbon follows the equation k=(4.5xx10^(11)s^(-1))e^(-28000K//T). Calculate E_(a).

The decomposition of hydrogen peroxide can be slowed by addition of a small amount of acetamide. The later acts as a:

The decomposition of H_2O_2 rate is decreased by ................

The decomposition of hydrocarbonfollows the equation k=(4.5xx10^(11)s^(-1))e^(-28000K//T) Calculate E_(a).

The decomposition of H_2O_2 may be checked by adding a small quantity of phosphoric acid. This is an example of :

The decomposition of H_(2)O_(2) may be checked by adding a small quantity of phosphoric acid. This is an example of