Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

31101.

The decomposition ofH_2O_2 can be slowed down by the addition of small amount of phosphoric acid which act as :

Answer»

Stopper
Detainer
Inhibitor
Promoter

Answer :C
Discussion
31102.

The decomposition of ethers by KI or HBr is called-

Answer»

Zerewitinoff's reaction
ZIESEL's method
Williamson's method
Hell-Volhard-Zelinsky reaction

Solution :Decomposition of ether by HI or HBR is called Ziesel's method.
Discussion
31103.

The decomposition of dimethyl ether leads to the formation of CH_(4),H_(2) and CO and the reaction rate is given by Rate =k[CH_(3)OCH_(3)]^((3)/(2)) The rate pressure is measured in bar and time in minutes ,then what are the units of rate and rate constants?

Answer»

Solution :Where ,PRESSURE is in bar and time is in minute.
`therefore` The unit of rate =bar `MIN^(-1)`
Rate =`k("Pressure"(CH_(3)OCH_(3))^((3)/(2)))/("Time")`
unit of k=`time^(-1)((1)/("pressure"))^(-1)`
`min^(-1)((1)/("bar"))^((3)/(2)-1)="bar"^(-(1)/(2)) "min"^(-1)`
Discussion
31104.

The decomposition of dinitrogen pontoxide(N_2O_5) follows the first order rate law . Calculare the rate constant from the given data :

Answer»

Solution :APPLYING the formula,
`K=(2.303)/((t_2-t_1))LOG10([A_1])/([A_2])`
`=(2.303)/((1600-800))log 10 (1.45)/(0.88)=(2.303)/(800)xx0.2169`
`=6.24xx1^(-4)"sec"^(-1)`
Discussion
31105.

The decomposition of dimethyl ether leads to the formation of CH_(4),H_(2) and CO and the reaction rate is given by Rate =k[P_(CH_(3)OCH_(3))]^(3//2). If the pressure is measured in bar and time in minutes, then what are the units of the rate and rate constants ?

Answer»

Solution :In TERMS of PRESSURES, units of RATE `="bar "min^(-1)`
Units of `k=("Rate")/([P_(CH_(3)OCH_(3))]^(3//2))("bar min"^(-1))/("bar"^(3//2))="bar"^(-1//2)min^(-1).`
Discussion
31106.

The decomposition of dimethyl ether leads to the formation of CH_(4), H_(2) and CO and the reaction rate is given by Rate =k[CH_(3)OCH_(3)]^(3//2) The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e., Rate =k(p_(CH_(3)OCH_(3)))^(3//2) If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?

Answer»

Solution :In TERMS of pressures, units of rate = bar minutes`""^(-1)`
Units of `K=("Rate"("bar minutes"^(-1)))/([p_(CH_(3)OCH_(3))]^(3//2)("bar"^(3//2)))="bar"^(-1//2)"minutes"^(-1)`.
Discussion
31107.

The decomposition of dimethyl ether is a fractional order reaction. The rate of reaction is givenby rate = k (p_(CH_(3)OCH_(3)))^(3//2). If the pressure is measured in bar and time in minutes, then what are the units of rate and constant?

Answer»

<P>BAR `"min"^(-1), "bar"^(2) "min"^(-1)`
bar `"min"^(-1), "bar"^(2), "min"^(-1)`
`"bar"^(-1//2) "min"^(-1),"bar"^(2),"min"^(-1)`
bar `"min"^(-1), "bar"^(1//2) "min"^(-1)`

Solution :In TERMS of pressure
Rate `k = (P_(CH_(3)OCH_(3))^(3//2))`
Unit of rate = bar `"min"^(-1)`
Unit of rate constant = `("rate")/((p_(CH_(3)OCH_(3))^(3//2))`
`= ("bar" "min"^(-1))/("bar"^(3//2)) = "bar"^(-1//2) "min"^(-1)`
Discussion
31108.

The decomposition of Cl_2O_7 at 500K in the gas phase to Cl_2 and O_2 is a first order reaction . After 1 minutes at 500 K , the pressure of Cl_2O_7 falls from 0.08 to 0.04 atm. Calculate the reate constant in s^(-1).

Answer»

Solution :`k = (2.303)/TLOG.([A_0])/([A])impliesk = (2.303)/(1 min)LOG.([0.08])/([0.04])`
`k = 2.303log 2 = ? k = 2.303xx0.3010`
`k = 0.6932 "min"^(-1)`
`k = ((0.6932)/60)s^(-1)impliesk=1.153xx10^(-2)s^(-1)`.
Discussion
31109.

The decomposition of complex organic compound into simpler compound with the help of enzyme is known as

Answer»

CATABOLISM
ANABOLISM
Fermentaiton
METABOLISM

ANSWER :A
Discussion
31110.

The decomposition of Cl_2O_7" at " 400 K in the gas phase to Cl_2 and O_2 is a first order reaction. after 55 seconds at 400K, the pressure of Cl_2 falls from 0.062 atm to 0.044 atm. Calculate the rate constant Calculate the pressure of Cl_2O_7after 100 sec of decomposition at this temperature.

Answer»

Solution :`6.23 XX 10^(-3) s^(-1) , 0.033` ATM
Discussion
31111.

The decomposition of Cl_(2)O_(7) at 400 K in the gas phase to Cl_(2) and O_(2) is a first orderreaction. (i) After 50 secondsat 400 K, the pressure of Cl_(2)O_(7) falls from 0.062 to 0.044 atm. Calculate the rate constant. (ii) Calculate the pressure of Cl_(2)O_(7) after 100sec of decomposition at this temperature.

Answer»

Solution :`apropP_(0)" and "(a-x)propP_(t)."Hence, "k=(2.303)/(t)log""(P_(0))/(P_(t))""(P_(t)=" pressure of "Cl_(2)O_(7)" at TIME t")`
(i) `t=50" SEC",P_(0)=0.062" atm",P_(t)=0.044" atm. "k=(2.303)/(50" s")log""(0.062" atm")/(0.044" atm")=6.86xx10^(-3)s^(-1)`
(II) `t=100" sec ",P_(t)=?k=6.86xx10^(-3)s^(-1)`
`6.86xx10^(-3)s^(-1)=(2.303)/(100s)log""(0.062" atm")/(P_(t))`
`log""(0.062)/(P_(t))=0.2979" or "(0.062)/(P_(t))="Antilog"0.2979=1.986" or "P_(t)=0.0312" atm"`
Discussion
31112.

The decomposition of Cl_2O_7,at 400 K in the gas phase to Cl_2 and O_2 is a first order reaction : Calculate the pressure of Cl_2O_7after 100 s of decomposition at this temperature

Answer»

SOLUTION :C = 0.033 ATMOSPHERE.
Discussion
31113.

the decomposition of ammonia on tungsten surface at 500K follows zero order kinetics. The Half-life period of this reaction is 45 minutes when the initial pressure is 4 bar. The half-life period (minutes) of the reaction when the initial pressure is 16 bar at the same temperature is

Answer»

`120`
`60`
`240`
`180`

Solution :For a ZERO order reaction,
`t_(1//2)PROPA` (initial concentration of initial pressure)
`(t_(1//2)_(1)prop_(1)`
`(t_(1//2)_(2)propP_(2)`
`((t_(1//2))_(2))/((t_(1//2))_(1))=(P_(2))/(P_(1)),((t_(1//2))_(2))/(45)=(16)/(4)`
`(t_(1//2))_(2)=(16)/(4)xx45=180` min
Discussion
31114.

The decomposition of ammonia on tungsten surface at 500 K follows zero order kinetics . The half-life period of this reaction is 45 minutes when the initial pressure is 4 bar . The half life period (minutes) of the reaction when the initial pressure is 16 bar at the same temperature is

Answer»

120
60
240
180

Solution :For a zero ORDER reaction
`t_(1//2) PROP a_(0)` (initial CONCENTRATION or initial pressure )
`(t_(1//2))_(1) prop P_(1)`
`(t_(1//2))_(2) prop P_(2)`
`((t_(1//2))_(2))/((t_(1//2))_(1)) =(P_(2))/(P_(1)) , (t_(1//2))_(2) = (16)/(4)`.
`(t_(1//2))_(2) = (16)/(4) XX 45` = 180 MIN
Discussion
31115.

The decomposition of ammonium nitrate gives …………………

Answer»

SOLUTION :NITROUS OXIDE
Discussion
31116.

The decomposition of ammonia on tungsten surface at 500 K follows zero order kinetics. The half-life period of this reaction is 45 minutes when the initial pressure is 4 bar. Find the half-life period (in minutes) of the reaction when the initial pressure is 16 bar at the same temperature.

Answer»


Solution :For a zero ORDER reaction,
`t_(1//2) PROP a_(0)` (initial concentration or initial pressure)
`(t_(1//2))_(1) prop P_(1)`
`(t_(1//2))_(2) prop P_(2)`
`(t_(1//2))_(2)/(t_(1//2))_(1) = P_(2)/P_(1), (t_(1//2))_(2)/45 = 16/4`
`(t_(1//2))_(2) = 16/4 xx 45 = 180` MIN
Discussion
31117.

The decomposition of ammonia gas on platinum surface has a rate constant k = 2.5 xx10^(-4)"mol L"^(-1)s^(-1) . What is the order of the reaction ?

Answer»

FIRST ORDER
SECOND order
THIRDORDER
ZERO order

Answer :D
Discussion
31118.

The decomposition of AB_2 to AB and B is first-order with k = 2.8 xx 10^(-7)s^(-1) at 1000^@CAB_2 to AB + BAtomic weights of A and B are 12 and 32 respectively.(i) Find the half-life of this reaction at 1000^@C.(ii) How many days would pass before 1 g of AB_2 had decomposed to theextent that 0.60 g of AB_2remained? (iii) With reference to (ii), how many grams of AB would be present after this length of time?(iv) How much of a 1-g sample of AB_2would remain after 35 days?

Answer»

SOLUTION :28.58 DAYS, 20.84 days, 0.23 G, 0.43 g
Discussion
31119.

The decomposition of acetaldehyde by I_(2)catalyst is an example of ........... catalysis.

Answer»

SOLUTION :HOMOGENEOUS
Discussion
31120.

The decomposition of acetaldehyde is a reaction of the order

Answer»

1
2
1.5
2.5

Solution :`CH_3CHO to CH_4 + CO,R = K[ CH_3CHO]^(1//2)` ORDER= 1.5
Discussion
31121.

The decomposition of a substance 'R' takes place according to fl rst order kinetics, Its initial concentration is reduced to 1/8th in 24 s. The rate constant of the reaction si

Answer»

`1/24 s^(-1)`
`0.69 /(16S^(-1))`
`(In 2) /8 s^(-1)`
`1/8 s^(-1)`

SOLUTION :`K = 1/24 In a/(a//8) = 1/24 In 8`
`= 1/24 In 2^3= 1/8 In2 s^(-1)`
Discussion
31122.

The decomposition of A into products has value of k as 4.5xx10^(3)s^(-1) at 10""^(@)C and energy of activation 60" kJ mol"^(-1). At what ttemperature would k be 1.5xx10^(4)s^(-1) ?

Answer»

Solution :`k_(1)=4.5xx10^(3)s^(-1),T_(1)=10+273" K"=283" K",k_(2)=1.5xx10^(4)s^(-1),T_(2)=?,E_(a)=60" kJ mol"^(-1)`
APPLYING Arrhenius equation,
`log""(k_(2))/(k_(1))=(E_(a))/(2.303" R")((T_(2)-T_(1))/(T_(1)T_(2)))`
`log""(1.5xx10^(4))/(4.5xx10^(3))=(60000" J mol"^(-1))/(2.303xx8.314" JK"^(-1)" mol"^(1))((T_(2)-283)/(283T_(2)))`
or `log3.333=3133.63((T_(2)-283)/(283t_(2)))" or "(0.5228)/(3133.63)=(T_(2)-283)/(283T_(2))" or "0.0472T_(2)=T_(2)-283`
or `0.9528T_(2)=283" or "T_(2)=(283)/(0.9528)=297" K"=297-273""^(@)C=24""^(@)C.`
Discussion
31123.

The decomposition of A into product has value of k as as 4.5 xx10^3s^(-1)" at "10^@C and energy of activation 60"kJ mol"^(-1). At what temperature would k be 1.5xx10^4s^(-1) ?

Answer»

SOLUTION :`k_1=4.5xx10^3s^(-1)`
`T_1 = 10 + 273 K = 283 K`
`k_2=1.5x10^4s^(-1)`
`T_2=? , E_a=60" kJ MOL"^(-1)`

According to Arrhenius equation,
`LOG.k_2/k_1=E_a/(2.303R)[(T_2-T_1)/(T_1T_2)]`
or `log.(1.5xx10^4)/(4.5xx10^(3))=(60000"Jmol"^(-1))/(2.303xx8.314"JK"^(-1) mol^(-1))xx[(T_2-283)/(283T_2)]`
or , `log3.3333333=3133.63[(T_2-283)/(283T_2)]`
or `0.0472T_2=T_2-283`
or `0.9528T_2=283`
or `T_2=283/90.9528=297K=(297-273^@C)=24^@C`
Discussion
31124.

The decomposition of A into products has a value of k as 4.5 xx 10^(3) s^(-1) at 10^(@)C and energy of activation 60 kJ mol^(-1). At what temperature would k be 1.5 xx 10^(-4) s^(-1) ?

Answer»

Solution :Given, `T_(1) = 10^(@)C + 273 = 283 K`
`k_(T_(1)) = 4.5 xx 10^(3) sec^(-1)`
`E_(a) = 60 KJ mol^(-1) =6 xx 10^(3) J mol^(-1)`
`T_(2) = ?`
`k_(T_(2)) = 1.5 xx 10^(4) sec^(-1)`
We know that
`log.(k_(T_(1))/(k_(T_(1)))) = (E_(a))/(2.303 R)[(T_(2)-T_(1))/(T_(1) xx T_(2))]`
On putting values
`log.(1.5 xx 10^(4))/(4.5 xx 10^(3)) = (60 xx 10^(3) J mol^(-1))/(2.303 xx 8.314)((T_(2)- 283)/(283 T_(2)))`
`0.523 = 3133.63((T_(2)-283)/(283 T_(2)))`
`(T_(2) - 283)/(283 T_(2)) = 1.67 xx 10^(-4)`
`T_(2) - 283 = 0.0472 T_(2)`
`0.953 T_(2) = 283`
`T_(2) = 297 K`
`T_(2) = 24^(@) C`
Discussion
31125.

The decomposition of A into product has value of k as 4.5xx10^(3)s^(-1) at 10 ""^(@)C and energyof activation 60 kJ "mol"^(-1). At what temperature would k be 1.5xx10^(4)s^(-1)?

Answer»

Solution :`k_(1)=4.5xx10^(3)s^(-1), T_(1)=10+273K=283K, k_(2)=1.5xx10^(4)s^(-1), T_(2)=?, E_(a)=60"kJ MOL"^(-1)`
Applying Arrhenius equation and substituting the values, we get
`"log"(k_(2))/(k_(1))=(E_(a))/(2.303R)((T_(2)-T_(1))/(T_(1)T_(2)))`
or `"log"(1.5xx10^(4))/(4.5xx10^(3))=(E_(a))/(RT)= -(60000"J mol"^(-1))/(2.303xx8.314JK^(-1)"mol"^(-1))((T_(2)-283)/(283T_(2)))`
or`log 3.333=3133.63 ((T_(2)-283)/(283T_(2))) or (0.5228)/(3133.63)=(T_(2)-283)/(283T_(2))`
or `0.0472T_(2)=T_(2)-283 or 0.9528T_(2)=283`
or `T_(2)=(283)/(0.9528)=297K=(297-273)""^(@)C=24""^(@)C`.
Discussion
31126.

The decomposition of A into product has value of k as 4.5xx10^(3) s^(-1) at 10^(@)C and energy of activation 60 KJ mol^(-1) .at what temperature would k be 1.5xx10^(4)s^(-1)?

Answer»

Solution :REACTION A `to` Product
`T_(1)=10^(@)C=10+273=283 K` and
`K_(1)=4.5xx10^(3)s^(-1)`
`E_(a)=60 KJ mol^(-1)=60000J mol^(-1)`
If `K_(2)=1.5xx104 s^(-1)` so temperature `T_(2)`=(?)
The ARRHENIUS equation is as under.
log `(K_(1))/(K_(2))=(E_(a))/(2.303)((T_(2)-T_(1))/(T_(1)T_(2)))`
`therefore ((1.5xx10^(4))/(4.5xx10^(3)))=(60000 J mol^(-1))/(2.303xx(8.314 JK^(-1) mol^(-1)))((T_(2)-283)/(T_(2)xx283))`
`therefore log 0.5228=(6000K)/(2.303xx8.314)((T_(2)-283)/(283 T_(2)))`
`therefore (T_(2)-283)/(T_(2))=(0.5228xx2.303xx8.314xx283)/(60000)`
`therefore T_(2)-283=(0.0472)T_(2)`
`therefore (T_(2)-0.0472 T_(2))=283`
`therefore 0.9528 T_(2)=283`
`therefore T_(2)=(283)/(0.9528)=297.02 K=24.02^(@)`C
Discussion
31127.

The decomposition of a compound P, at temperature T according to the equation 2P_((g)) rarr 4Q_((g)) +R_((g)) +S_((l))is the first order reaction. After 30 minutres from the start of decomposition in a closed vessel, the total pressure developed is found to be 317 mm Hg and after a long period of time the total pressure observed to be 617 mm Hg. Calculate the total pressure of the vessel after 75 mintute, if volume of liquid S is supposed to be negligible. Also calculate the time fraction t_(7//8). Given : Vapour pressure of S(l) at temperature T = 32.5 mm Hg

Answer»

<P>

SOLUTION :`p_(t)=379.55" MIN HG, "t_(7//8)=399.96` min
Discussion
31128.

The decomposition of a compound is found to follow a first order rate law. If it takes 15 minutes for 20 percent of original material to react, calculate (i) specific rate constant (ii) the time at which 10 percent of the original material remains unreacted, (iii) the time it takes for the next 20 percent of the reactant left to react after the first 15 minutes.

Answer»


SOLUTION :(i) `k=(2.303)/(t)LOG""(a)/(a-x)=(2.303)/(15" min")log""(a)/(a-0.20a)=0.01488" min"^(-1)`
(ii) `t=(2.303)/(k)log""(a)/(0.10a)=(2.303)/(0.01488)log10=154.77" min".`
(iii) In first 15 minutes, `20%` has reacted. `:.` AMOUNT LEFT unreacted `=80%` of `a=0.80` a
This is now initial CONCENTRATION. For next `20%` of this amount to react means `x=20%` of `0.80a=0.16a`
`:.""t=(2.303)/(k)log""(0.80a)/(0.80a-0.16a)=(2.303)/(0.01488" min"^(-1))log""(0.80)/(0.64)`
`=154.77" min "xxlog1.25=154.77xx0.0969" min "=15 "minutes"`
Discussion
31129.

The decomposition of A into product has value of K as 4.5 xx 10^(3) sec^(-1) at 10^@ C and energy of activation 60 kJ/mol. At what temperature would K be 1.5 xx 10^(4) "sec"^(-1).

Answer»

SOLUTION :`24^@` C
Discussion
31130.

The decomposition of a hydrocarbon follows the equation k=(4.5xx10^(11)s^(-1))e^(-28000" K"//"T") Calculate E_(a).

Answer»

SOLUTION :According to Arrhenius EQUATION, `k="A E"^(-E_(a)//"RT")`
`:.-(E_(a))/(RT)=-(28000" K")/(T)" or "E_(a)=28000" K"XX" R"=28000" K"xx8.314" JK"^(-1)" mol"^(-1)=232.79" kJ mol"^(-1).`
Discussion
31131.

The decomposition of a certain mass of CaCO_(3) gave 11.2dm^(3) of CO_(2) gas at STP. The mass of KOH required to completely neutralize the gas is

Answer»

56 g
28 g
42 g
20 g

Solution :`{:(2KOH,+,CO_(2)rarrK_(2)CO_(3)+H_(2)O),(2(39+16+1),,22.4dm^(3)),(=112g,,"at STP"):}`
22.4 `dm^(3)` of `CO_(2)` at STP required KOH = 112 g
`THEREFORE 11.2dm^(3)` of `CO_(2)` at sTP will required KOH
= 56 g
Discussion
31132.

The decomposition of a certain mass of CaCO_(3) gave 11.2 dm^(3) of CO_(2) gas at STP. The mass of KOH required to completely neutralise the gas is:

Answer»

56g
28g
42g
20g

Solution :`11.2dm^(3)` of `CO_(2)` at `STP=(1)/(2)"MOLE"CO_(2)`
`KOH+CO_(2)rarrKHCO_(3)`
`(1)/(2)` mole `CO_(2)` will be neutralised by `(1)/(2)` mole KOH,i.e.,28g KOH
Discussion
31133.

The decomposition of a certain mass of CaCO_(3) gave 11.2 dm^(3) of a CO_(2) at S.T.P. The mass of KOH required to completely neutralize the gas is

Answer»

`56 g`
`28g`
`42G`
`20g`

Solution :`underset(112G)underset(2(39+16+1))(2KOH)+underset("at S.T.P.")underset(22.4 L)(CO_(2))toK_(2)CO_(3)+H_(2)O`
`22.4 DM^(3)` of `CO_(2)` at N.T.P. required KOH = 112 g
`11.2 dm^(3)` of `CO_(2)` at S.T.P. will require KOH = 56 g
Discussion
31134.

The decomposition of a certain mass of CaCO_(3) gave 11.2 dm^(3) of CO_(2) gas at STP. The mass of KOH required to completely neutralise the gas is

Answer»

56 g
28 g
42 g
20 g

Solution :Weight of `11.2 DM^(3)` of `CO_(2)` GAS at STP is
`44//2=22g`
`underset(56 g)(KOH)+underset(44 g)(CO_(2))to KHCO_(3)`
KOH REQUIRED for complete NEUTRALISATION of 22 g `CO_(2)` is
`(56)/(44)xx22=28 g`.
Discussion
31135.

The decay of a radioactive element follows first order kinetics, as a result

Answer»

Half-life period = constant/k, where k is the decay constant
Rate of decay is independent of temperature
Rate can be changed by changing chemical conditions
The element will be completely transformed into a NEW element after EXPIRY of two half-life period

Solution :For `1^(ST)` ORDER `t_(1//2) = 0.693 K^(-1)`. Rate of decay is independent of temperature.
Discussion
31136.

The decimal equivalent of 2/5 may be written upto four significant figures as :

Answer»

0.4
`4.0 xx 10^(-1)`
`0.4000`
`0.04000`

SOLUTION :`2/5 = 0.4` . The result can be EXPRESSED upto FOUR significant figures as 0.4000.
Discussion
31137.

The decay constant of radioactive substance is 0.173 ("years")^(-1) . Therefore

Answer»

One sixth of the RADIOACTIVE substance will be left after 8 years
Half life of the radioactive substance is 1/0.173 YEAR
Nearly 63% of the radioactive substance will decay in 1/0. 173 years
All the above statements are true.

Answer :C
Discussion
31138.

The decay constant of a radioactive element is 3 xx 10^(-6) "min"^(-1). Its half-life is

Answer»

`2.31 XX 10^(5)` min
`2.31 xx 10^(6)` min
`2.31 xx 10^(-6)` min
`2.31 xx 10^(-7)` min

Solution :`t_(1//2) = (0.693)/(lamda) = (0.693)/(3 xx 10^(-6) "min"^(-1)) = 2.31 xx 10^(5)` min
Discussion
31139.

The decay constant of Ra^(226) " is " 1.37 xx 10^(-1)) s^(-1). A sample of Ra^(226) having an activity of 1.5 millicurie will contain.... atoms

Answer»

`4.1 XX 10^(18)`
`3.7 xx 10^(17)`
`2.05 xx 10^(15)`
`4.7 xx 10^(10)`

SOLUTION :1 milli curie `= 3.7 xx 10^(7) dps`
1.5 milli curie `= 5.55 xx 10^(7) dps`
`(5.55 xx 10^(7))/(N_(0)) = lamda = 1.37 xx 10^(-11)`
Discussion
31140.

The decay constant of a radioactive sample is 'lamda'. The half-life and mean life of the sample are respectively

Answer»

`(1)/(lamda), (LN 2)/(lamda)`
`(ln 2)/(lamda), (1)/(lamda)`
`lamda ln 2, (1)/(lamda)`
`(lamda)/(ln 2), (1)/(lamda)`

Solution :`t_(1//2) = (log_(E)2)/(lamda)`, Average life `= (1)/(lamda)`
Discussion
31141.

The decay constant of _88^226 Ra is 1.37 times 10^-11 sec^-1. A sample of _88^226 Ra having an activity of 1.5 millicurie will contain ….atoms. The blank can be correctly filled by,

Answer»

`4.05 TIMES 10^18`
`3.7 times 10^17`
`2.05 times 10^15`
`4.7 times 10^10`

ANSWER :A
Discussion
31142.

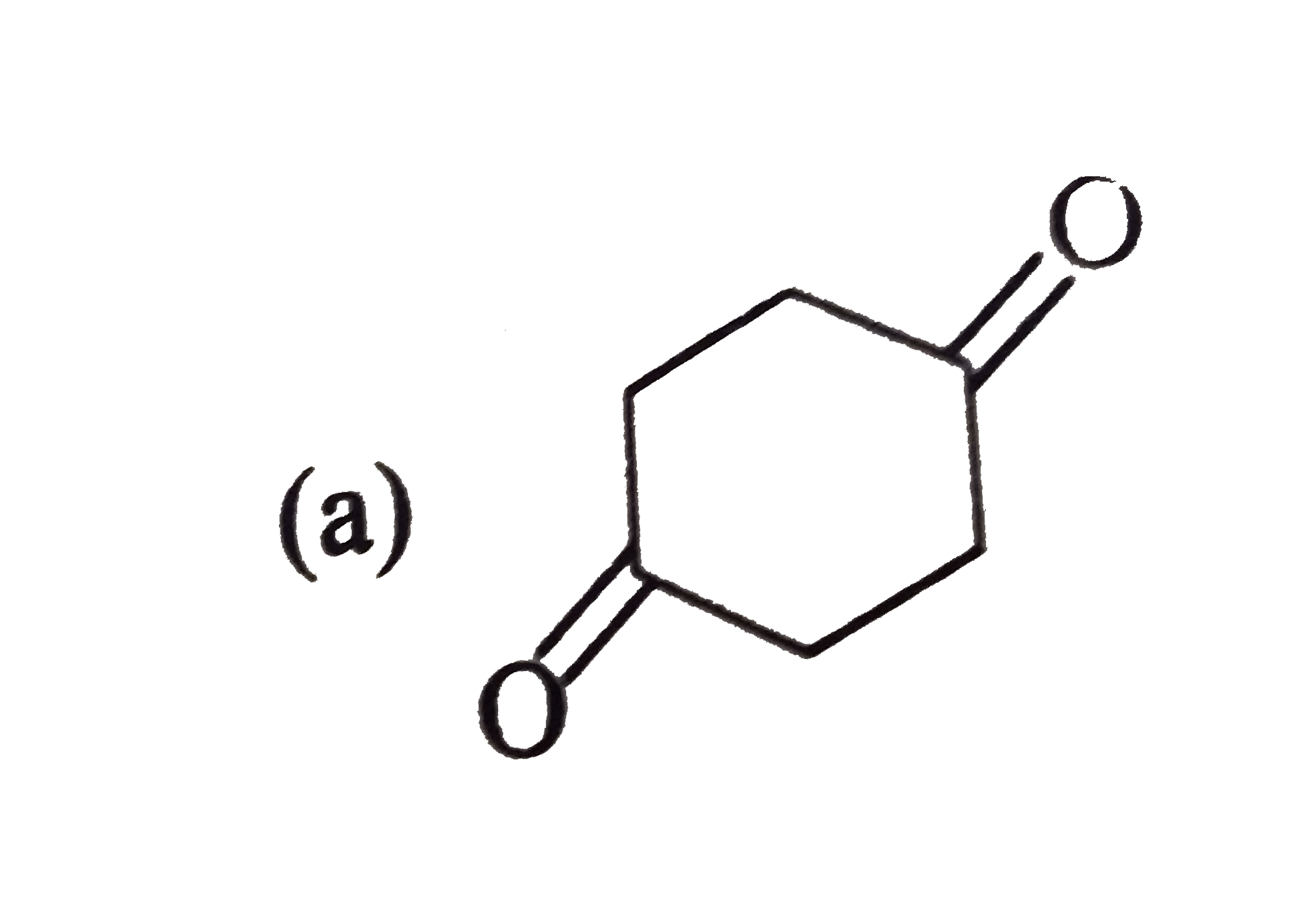
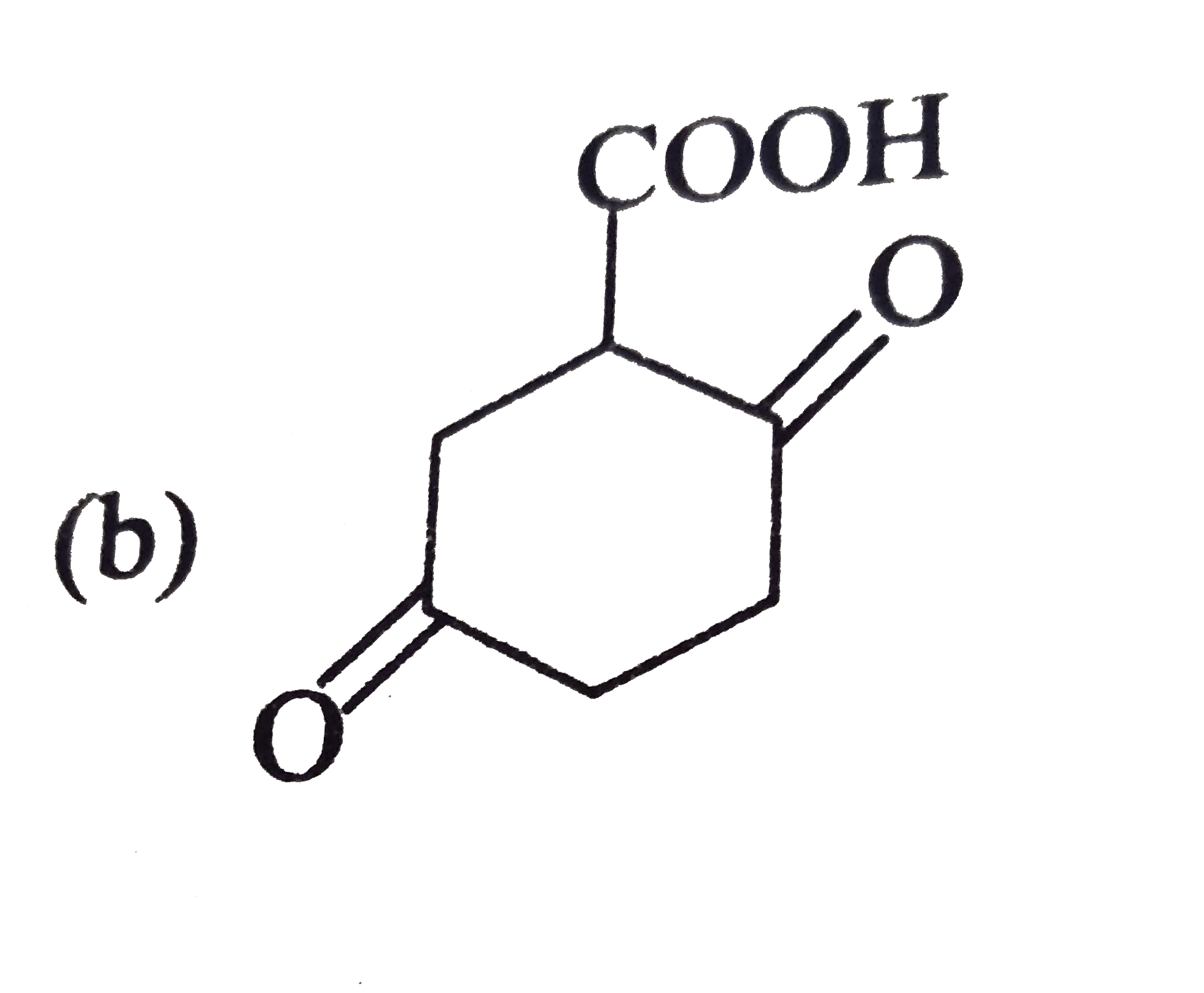
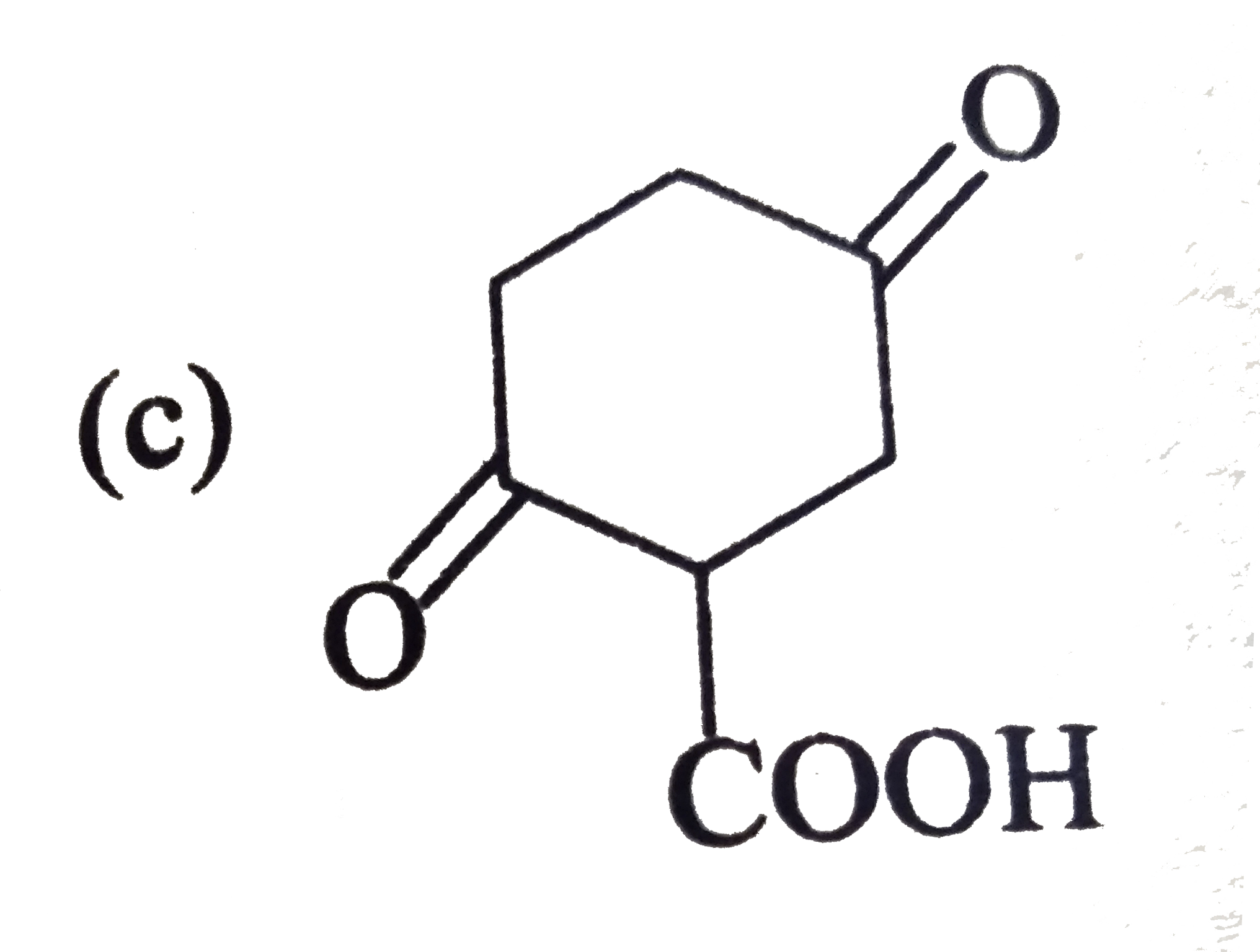
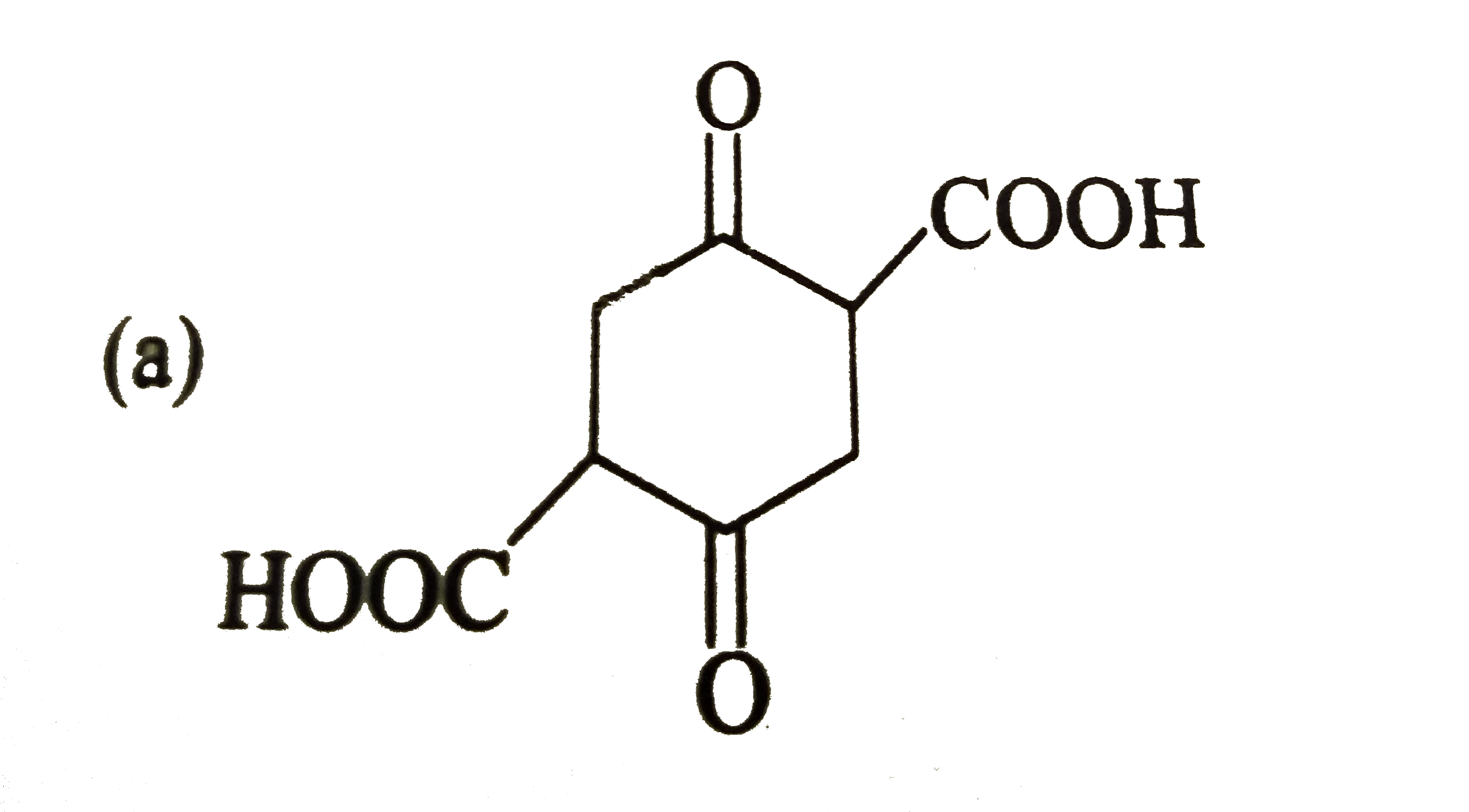
The decarboxylation of beta - ketoacids, beta, gamma - unsaturated acid and geminal diacid proceed through the formation of cyclic transition state in presence of heat. CH_(3)-overset(O)overset("||")C-CH_(2)-overset(O)overset("||")C-OHoverset(Delta)rarrCH_(3)-overset(O)overset("||")C-CH_(3) Mechanism: Find the correct product of following reaction: H_(3)C-CH=CH-CD_(2)-overset(O)overset("||")C-OHoverset(Delta)rarr

Answer»

`H_(3)C-CH_(2)-CH=CD_(2)`
`CH_(3)-CH=CH-CHD_(2)`
`H_(3)C-underset(CHD_(2))underset(|)C=CH_(2)`
NONE of these

Answer :A
Discussion
31143.

The decasing nucleophilic order of the following compounds is: i. H_(2)O, ii. H_(2)S, iii. H_(2)Se, iv. H_(2)Te

Answer»

`(i) GT (ii) gt (iii) gt (iv)`
`(iv) gt (iii) gt (ii) gt (i)`
`(IIII) gt (i) gt (ii) gt (iv)`
`(iv) gt (ii) gt (i) gt (iii)`

Solution :Basically and nucleophilicity orders are reversed, Have different nucleophilic CENTRE and belong to the same group.
Nuclophillcity: `H_(2)OTE gt H_(2)Se gt H_(2)S gt H_(2)Te`
Discussion
31144.

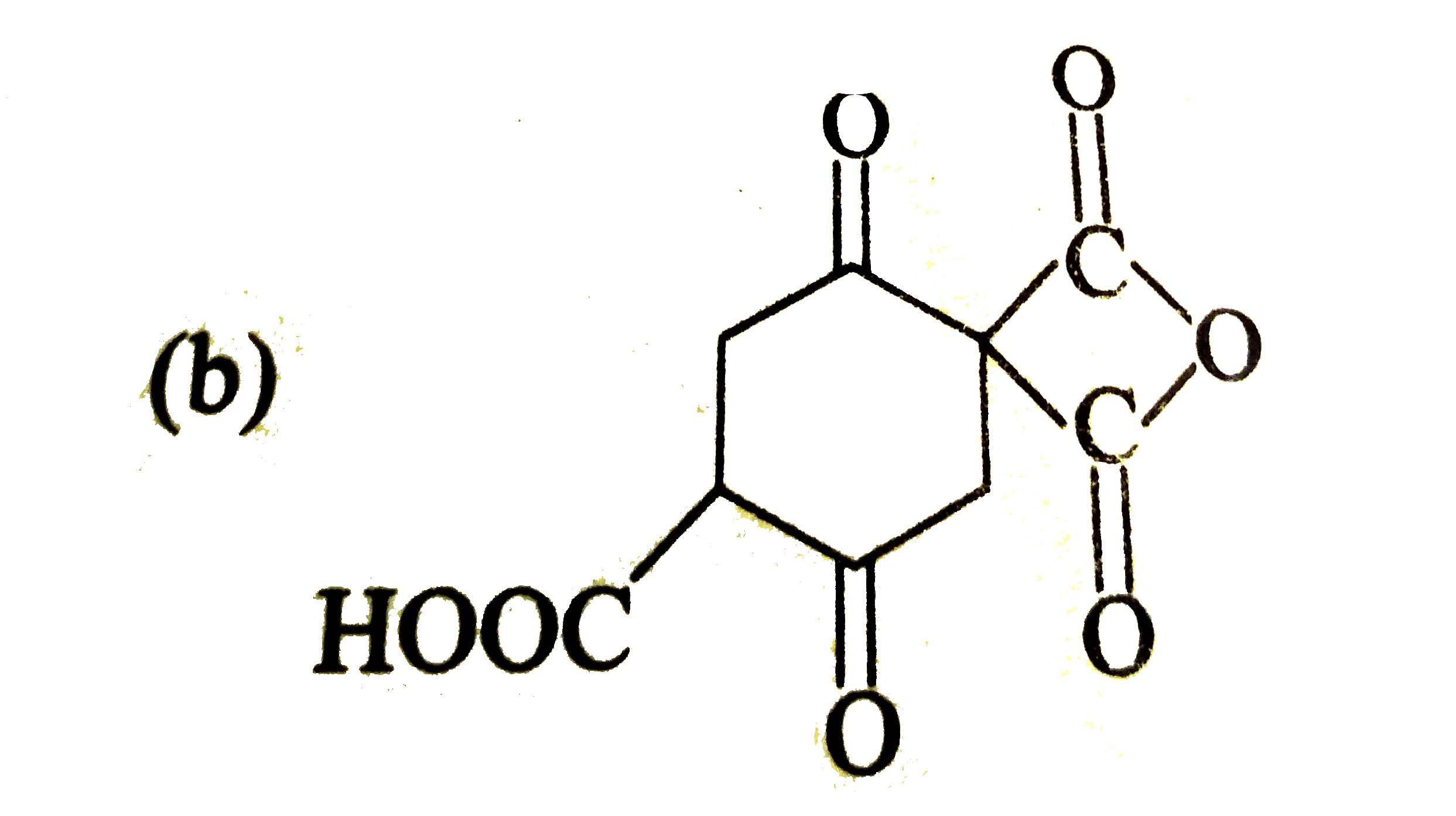
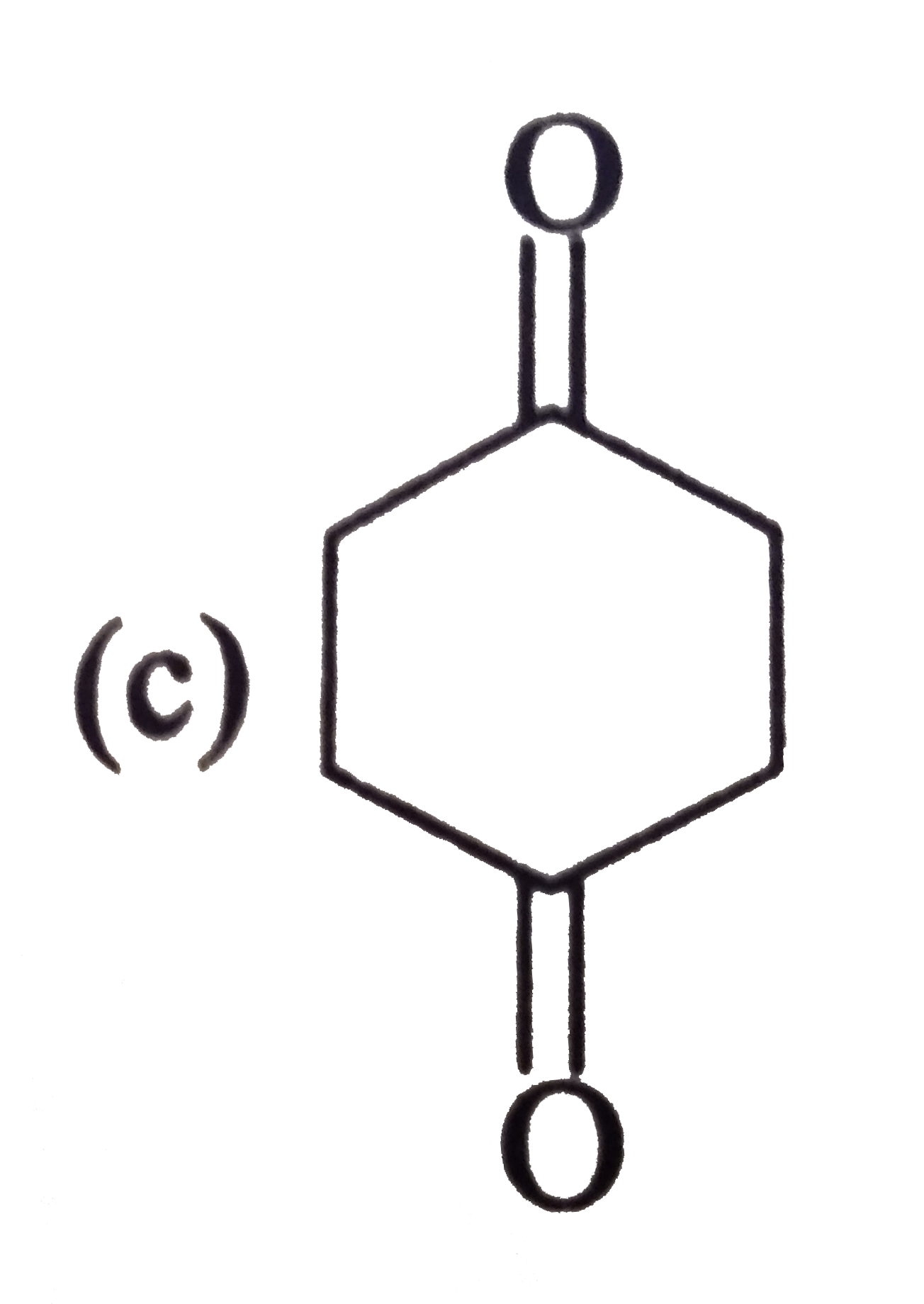
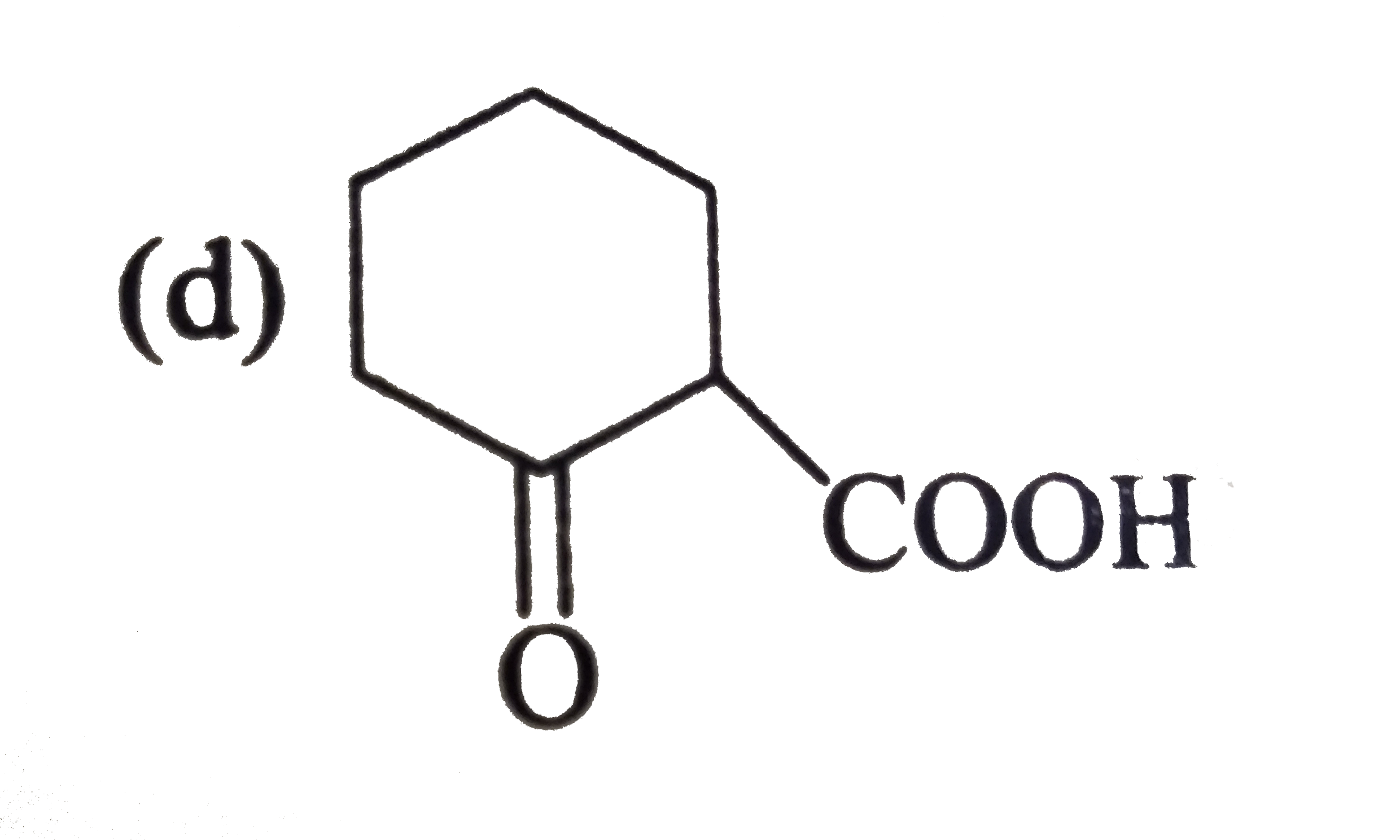
The decarboxylation of beta - ketoacids, beta, gamma - unsaturated acid and geminal diacid proceed through the formation of cyclic transition state in presence of heat. CH_(3)-overset(O)overset("||")C-CH_(2)-overset(O)overset("||")C-OHoverset(Delta)rarrCH_(3)-overset(O)overset("||")C-CH_(3) Mechanism: Find the product of following reaction :

Answer»




ANSWER :A
Discussion
31145.

The decarboxylation of beta - ketoacids, beta, gamma - unsaturated acid and geminal diacid proceed through the formation of cyclic transition state in presence of heat. CH_(3)-overset(O)overset("||")C-CH_(2)-overset(O)overset("||")C-OHoverset(Delta)rarrCH_(3)-overset(O)overset("||")C-CH_(3) Mechanism:

Answer»




ANSWER :C
Discussion
31146.

The decarising basic order of the following is: i. F_(3)CSO_(3)^(o-), ii. Cl_(3)C-COO^(o-) iii. PhSO_(3)^(o-), iv. MeSO_(3)^(o-)

Answer»

`(i) gt (ii) gt (III) gt (iv)`
`(iv) gt (iii) gt (ii) gt (i)`
`(ii) gt (iv) gt (iii) gt (i)`
`(iv) gt (ii) gt (i) gt (iii)`

SOLUTION :Stronger the ACI, WEAKER the `C_(B)`
i. Sulphonic acids are stronger than carboxylic acids.
ii. Aromatic sulphonic acids are stronger than alipatic sulphonic acids.
iii. More the number of number of `EWG` stronger is the acid.
Acidic:
`F_(3) CSO_(3)H gt PhSO_*3)H gt MeSO_(3)^(o-) lt MeSO_(3)H gt Cl_(3)CCOOH`
Basic:
`F_(3)CSO_(3)^(o-) lt PhSO_(3)^(o-) lt MeSI_(3)^(o-) lt Cl_(3)CCO overset(o-)(O)`
Discussion
31147.

Namethe decarboxylatingagent .

Answer»

SODA lime
lime water
quick lime
lime of milk

Answer :A
Discussion
31148.

The decahydrate form of sodium carbonate i.e. washing soda on starding in air effloresces and crumbles to powder.The number of water molecule(s) present in the compound formed is:

Answer»


SOLUTION :`Na_2CO_3. 10H_2O UNDERSET(-9H_2O)OVERSET("efforesces")toNa_2CO_3. H_2O`(MONOHYDRATE)
Discussion
31149.

The deBroglie wavelength of an electron travelling at 1% of the speed of light is(h=6.6xx10^(-4)Js, mass of electron =9.0xx10^(-31)kg

Answer»

`24.4xx10^(-10)m`
`244nm`
`24.4"PM"`
`244 "pm"`

ANSWER :D
Discussion
31150.

The de Broglie wavelength of a tennis ball of mass 60 g moving with a velocity of 10ms^(-1) is approximately (h=6.6xx10^(-34)Js)

Answer»

`10^(-31)m`
`10^(-16)m`
`10^(-25)m`
`10^(-33)m`

SOLUTION :`lamda=h/(MV)=(6.63xx10^(-34)kg m^(2)s^(-10))/(0.060kgxx10ms^(-10))=10^(-33)m`
Discussion