Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

5101.

The M.I. of a cyclinder about the axis of symmetry is equal to the M.I. about the axis passing through its centre and perpendicular to its length. The ratio of its length to the radius is :

Answer»

`sqrt(3):1`
`1:sqrt(3)`
`sqrt(2):1`
`1:sqrt(2)`

Solution :Here `(MR^(2))/(2)=[(MR^(2))/(4)+(ML^(2))/(12)]`
`therefore (L)/(R)=sqrt(3)/(1)`
Discussion
5102.

Capacitive reactance of a capacitor for a D.C. circuit is.......

Answer»

0
`omegaC`
`1/(omegaC)`
INFINITE

SOLUTION :`X_C=1/(2pifC)` for D.C. SUPPLY f=0
`X_C=1/0`= infinite
Discussion
5103.

In a plane Electromagnetic wave the electric field oscillates sinusoidally at a frequency of 2.0 X 10^(10) Hz & amplitude 48 Vm^(-1). show that the average energy density of the electric field (vec(E )), is equal to average energy density of the magnetic field (vec(B))

Answer»

Solution :Average energy magnetic field `vec(E )`
`U_(E ) "" (1)/(2)CDOT epsilon_(0) E^(2) `
Average energy density of electric field `vec(B)`
`U_(E ) = (1)/(2 mu_(0)) cdot B^(2)`
But E = CB & `C^(2) = (1)/(mu_(0)epsilon_(0))`
`U_(E ) = (1)/(2) cdot epsilon_(0) E^(2)= (1)/(2) cdot epsilon_(0)(CB)^(2)`
`U_(E )= (1)/(2) cdot epsilon_(0) (1)/(mu_(0)epsilon_(0)) B^(2) = (1)/(mu_(0) epsilon_(0)) B^(2) = U_(B)`
`THEREFORE U_(E ) = U_(B)`
Discussion
5104.

A photoelectric cell gives zero current when maintained at 2V negative potential. The energy of most energetic photoelectrons is

Answer»

2eV
2J
4eV
4J

Solution :`K_(max)` in eV=stopping potential `V_(0)` in VOLT.
`implies K_(max)=2eV`
Discussion
5105.

Light of uniform intensity shines perpendicularly on a totally absorbing surface fully illuminating the surface . If the area of the surface is decreased

Answer»

The radiation PRESSURE increases and the radiation FORCE increases
The radiation pressure increases and the radiation force DECREASES
The radiation pressure STAYS the same and the radiation force increases
The radiation pressure stays the same and the radiation force decreases

ANSWER :D
Discussion
5106.

Lens is kept nearer to eye to observe a small thin net of wire at 8 cm distance by magnifying glass of 10 cm focal length, then magnification = …....

Answer»

5
8
10
20

Solution :u=-8 CM , f= +10 cm
`1/v-1/u=1/f`
`therefore 1/v=1/f+1/u`
`=(1)/(10)+(1)/(-8)=(1)/(10)-1/8=(4-5)/(40)`
`1/v=(-1)/(40)`
`therefore v=-40` cm
Now `m=v/u=(-40)/(-8)=5`
SECOND METHOD :
`m=(f)/(f+u)=(10)/(10-8)=(10)/(2)=5`
Discussion
5107.

A short bar magnet placed with its axis at 30^(@) with a uniform external magnetic field of 0.25T. T experiences a torque of magnitude equal to 4.5 xx 10^(-2)J. What is the magnitude of magntic moment of the magnet?

Answer»

Solution :When magnetic dipole moment `overset(to) (m)` of a bar magnet makes angle `theta` with external uniform magnetic field `overset(to) (B)` TORQUE `overset(to) (TAU)` exerted on it is GIVEN by,
`overset(to)(tau ) = overset(to) xx overset(to)(B)""...(1)`
`therefore tau = mB SIN theta""...(2)`
`therefore m= (tau)/( B sin theta)`
`= (4.5 xx 10^(-2) )/( (0.25) (sin 30^@) )`
`= (0.045)/( (0.25) (0.5) )`
`therefore m= 0.36` (ampere)(metre) `""^(2)`
Discussion
5108.

In an n-type semiconductor, the donor energy level lies

Answer»

at the CENTRE of the ENERGY gap.
just below the CONDUCTION band.
just above the VALANCE band.
in the conduction band.

Answer :b
Discussion
5109.

In the above problem if potential on its surface is .V.. Potential at distance (r )/(2) from its centre is _____

Answer»

`(11)/(13)V`
`(14)/(11)V`
`(22)/(13)V`
`(23)/(16)V`

Answer :D
Discussion
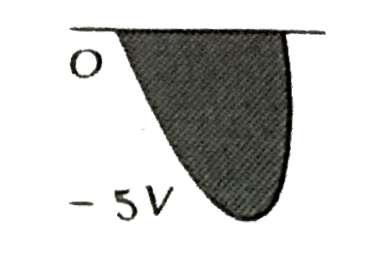
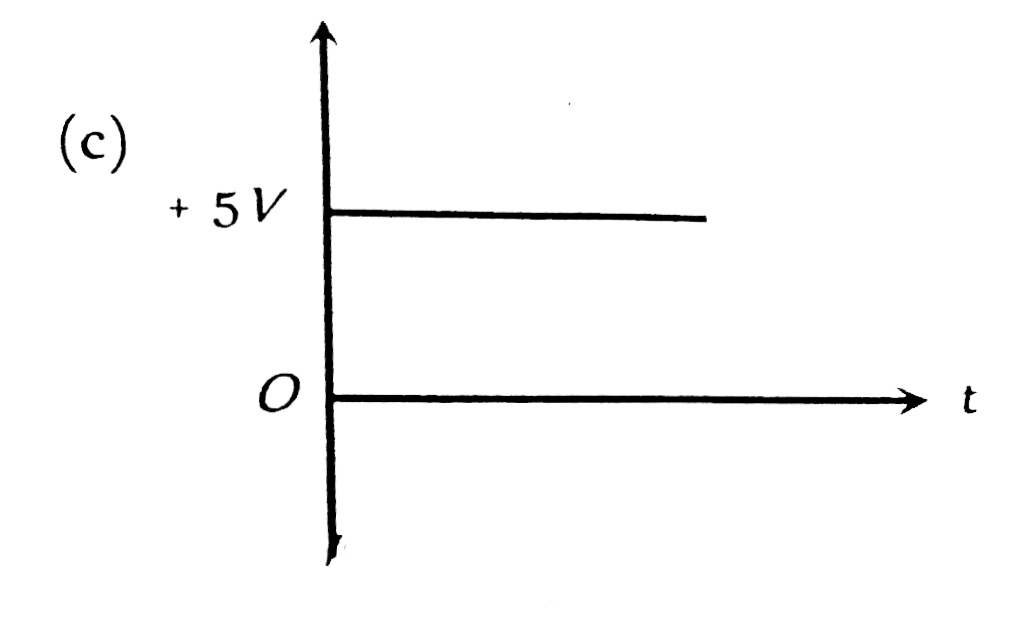
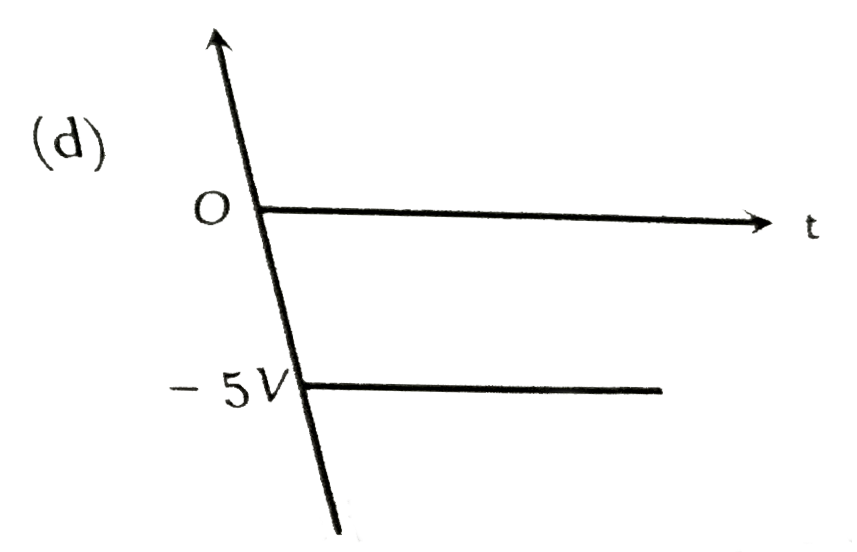
5110.

The output in the circuit of figure is taken across a capacitor. It is as shown in figure

Answer»




ANSWER :C
Discussion
5111.

A 100 W and a 500 W bulbs are joined in series and connected to the mains. Which bulb will glow brigher ?

Answer»

Solution :Let `R_(1) and R_(2)` be the resistance of the two bulbs. If each bulb is connected separately to the mains of voltage V, then `P_(1)=(V^(2))/(R_(1)) and R_(2)=(V^(2))/(R_(2))`
`therefore""(P_(1))/(P_(2))=(R_(2))/(R_(1)) (or) (R_(1))/(R_(2))=(P_(2))/(P_(1))=(500)/(100)=5`
If the two bulbs are in series with the mains, the same current .i. flows through each of them.
Let `P_(1) and P_(2)` be the powers dissipated by two bulbs, turn `(P_(1)^(1))/(P_(2)^(1))=(R_(1))/(R_(2))=5 or P_(1)^(1)=5P_(2)^(1)`
SINCE 100 WATT bulb dissipates more POWER, it glows brigher
Discussion
5112.

Displacement vecd _(1) is in the yz plane 63.0^(@) from the positive direction of the y axis, has a positive z component , and has a magnitude of 4. 80 m. Displacement vecd _(2) is in the xz plane 30.0 ^(@) from the positive direction of the x axis, has a positive z component, and has magnitude 1.40m. What are (a) vec d _(1) . vecd_(2), (b) vecd _(1)x vecd _(1), and(c ) the angle between vecd _(1) and vecd_(2) ?

Answer»

Solution :`(a) 2.99 m ^(2) , (b) (1. 53hati + 5.19hatj - 2.64 HATK) m^(2) , (C ) 63.6 ^(@)`
Discussion
5113.

A cyclotron is used to accelerate

Answer»

both POSITIVELY and NEGATIVELY CHARGED particles
only NEGATIVE charged particles
only positively charged particles
neutron

Solution :`5950Omega`
Discussion
5114.

A convex lens of focal length 0.24 m and of refractive index 1.5 is completely immersed in water of refractive 1.33. Find the changes in the focal length of the lens.

Answer»

Solution :Lens in air, `(1)/(f_(G)) \= ( n _(g)-1) ((1)/(R_(1))-(1)/(R_(2)) )`, `(f_(g) = `FOCAL length in air )
`(1)/(0.24) = ( 1.5-1) ((1)/(R_(1))-(1)/(R_(2)))`
Lens in water, ` (1)/( f_(gw)) = ( (n_(g))/(n_(w))-1)= ( (1)/( R_(1)) - ( 1)/( R_(2)))`,`( f_(gw)` = focal length of lens in water )
`(1)/( f_(gw)) = ((1.5)/(1.3) -1) ( (1 )/( R_(1))- ( 1)/( R_(2))) `....(ii)
DIVIDING EQUATION (1) by (2),
`f_(gw) = 0.939m`
`:.` Change in focal length `= 0.699m ( with unit )
Discussion
5115.

in the circuit shown in the figure, each battery is of 5 V and has an internal resistance of 0.2 Omega What is the reading of the ideal voltmeter V

Answer»

Solution :As the internal resistance of an ideal voltmeter is INFINITE, the resistance of the battery ACROSS which it is connected will not change by its presence as`(1)/(r_(1))=(1)/(r)+(1)/(INFTY)impliesr_(1)=r`
Now, as the given eight batteries are discharging in series, i.e
`E_(eq) = 8 xx 5 = 40 V`
and `r_(eg) = 8 xx 0.2 = 1.6Omega`
So, current in the circuit, `I=(E_(eq)/(r_(eq))=(40)/(1.6)=25A`
`HENCE, potential difference across the required battery
`V=E- Ir = 5-25 xx 0.2 = 0V`
Discussion
5116.

A solid cyclindrical insulator of uniform density having length 4 and radius 2 contains charge Q. Find the value of the electric field at a distance L along the axis from one end. (L=length of insulator)

Answer»

`(Q)/(16piepsi_(0))(2-sqrt(17))`
`(Q)/(32piepsi_(0))(2+SQRT5)`
`(Q)/(16piepsi_(0))(sqrt5-sqrt(17))`
`(Q)/(16piepsi_(0))(2-sqrt(17)-sqrt5)`

ANSWER :D
Discussion
5117.

A boat is moving with a velocity vw= 5 km/hr relative to water. At time , the boat passes through a piece of cork floating in water while moving downstream. If it turns back at time t_(1)=30 min, (a) when the boat meet the cork again? (b) The distance travelled by the boat during this time.

Answer»

Solution :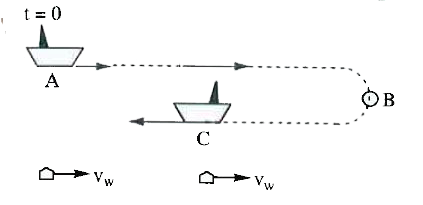
Consider an observer attached with cork. The BOAT has same speed upstream and downstream relative to cork. HENCE, if the boat travels for 30MIN, while moving away from cork, it travel the same TIME while approching the cork.
THEREFORE the boat meet thecork at T=2 60 min. = 1h The distance travelled by boat in this time
`S=V_(BW)xxT=5xx1=5 km`
Discussion
5118.

During Diwali festival, Rajender brought a new microwave oven in his house and told his wife Sarika to use the same carefully. He also told her that microwave oven is to used for slow heating of the vegetables and food articles upto moderate temperature as that will preserve the from the food. Further, the vegetables or flood items to be heated in oven are to be kept in a porecelain vessel and not in a matallic vessel. Read the above paragraph and answer and following questions: (i) What is the basic principle of working of microwave oven? (ii) Why is it advised to use porcelain vessel for heating the food items in microwave oven? (iii) What basic values do you learn from his study?

Answer»

Solution :(i) The basic principle of working of microwave oven is to create microwave radiations of siutable frequency
in the working space of oven, which may match the resonant frequency fall on food items containing
water molecules (like, fruits, vegetables,cereals etc.) placed in oven, the water molecules absorb these
radiations. As a result of it, the energy of water molecules increases. These molecules SHARE their energy
with neighbouring molecules. Due to it, the entire gets heated.
(ii) In microwave oven, a porcelain container is used for HEATING the food articles in the oven. It is so becuase
the size of the molecules of porcelain container is large and they vibrate and rotate with much smaller
frequency than that of microwave and hence can not absorb microwaves. Due to it, the porcelain container
REMAINS at relatively lower temperature.
(iii) We find that in a microwave oven, the SLOW and low heating of food will preserve the food values but fast
and intense heating will destroy the food values. The same is true in day to day life. Sudden rises may be
HARMFUL. Instead, steady rises are appricable.
Discussion
5119.

Ordinary light incident on a glass slab at the polarizing angle suffers a deviation of 22^(@). The value of angle of refraction is .......

Answer»

`74^(@)`
`22^(@)`
`90^(@)`
`34^(@)`

Solution :
From figure `theta_(p)=r+22^(@) ""..(1)`
Now from proof of Brewster.s law.
`theta_(p)+90^(@)+r=180^(@)`
`:.` From RESULT (1)
`r+22^(@)=r=90^(@)`
`:.2r=68^(@)`
`:.r=34^(@)`
Discussion
5120.

Derive an expression for the magnetic dipole moment of an orbiting electron.

Answer»

SOLUTION :REFER TEXT
Discussion
5121.

The charge density is maximum at ...........

Answer»


ANSWER :POINTED
Discussion
5122.

Fig shows the electric field lines due to a point positive charge. P and Q are two point in the electric field. i) What is the sign pf V_(P)-V_(Q)? ii) What is the sign of the potential energy difference of a small negative charge between Q and P? iii) What is the sign of work done by the field in moving a small positive charge from Q to P? iv)What is the sign of work done by external agent in moving a positive charge from Q to P?

Answer»

<P>

Solution :(i) Potential at point `V prop 1//r`. Therefore, `V_(P) gt V_(Q)`.
Hence sign of `V_(P)-V_(Q)` is positive.
(ii) If a negative CHARGE is placed at Q, it will move towards P.
SINCE, a charge moves from higher potential ENERGY to lower potential energy, `U_(Q) gt U_(P)`. Therefore, `U_(Q)-U_(P)` is positive.
(iii) If a small positive charge is placed at P, work done by the field in moving it to Q is positive. Hence, work done by the field in moving small positive charge from Q to P is negative.
(iv) Since in moving the positive charge from Q to P, external AGENT should do work against the field, the work done is positive.
Discussion
5123.

Electric potential in vole (in region) is given by v=6x+8y+4z^(2) Calculate the electric force (in N) acting on 2C point charge placed at origin.

Answer»


Solution :`E _(x) =-(delv )/(delx) =- 6 hati`
`E _(y) =-(delv)/(vely)=-8 hatj`
`E _(z) =-(delv)/(delz) =-8 z HATK`

`vecE_(n ET) ` AR origin` = sqrt(6^(2) +8^(2)) =10`
`implies|vecF| =|q vecE|=20N`
Discussion
5124.

What is the voltage gain of a transistor with load resistance 100 Omega and internal resistance 200 Omega ? Given that beta = 90.

Answer»

400
450
800
900

Solution :`A_v=betaR_L//R_i=450`
Discussion
5125.

A body projected vertically from the earth reaches a height equal to earth'sradius before returning ot the earth. The power exerted by the gravitational force is greatest:

Answer»

at the highestposition of the body.
at the instant just before the body hits the earth.
it remains CONSTANT all through.
at the instant just after the body is projected.

Solution :Power, `P=F.v`.
Since F and v are maximum when the body is just to HIT the each. so power EXERTED by earth WOULD also be max. at that instant.
Thus correct choice is (B).
Discussion
5126.

The work done in rotating a bar magnet f magnetic moment M from its unstable equilibrium positon to its stable equilibrium position in a uniform magnetic field B is

Answer»

`2MB`
`MB`
`-MB`
`-2MB`

ANSWER :D
Discussion
5127.

Asseration A bar magnetic is dropped into a long vertical copper tube. Even taking air resistance as negligible, the magnet attains a constant terminal velocity gets increased. Reason: The terminal velocity depends on eddy current produced in bar magnet.

Answer»

If both asseration and reason are true and reason ISTHE correct explanation of ASSERTION.
If both asseration and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If assertion is false but reason is true.

Solution :When the TUBE is hearted its RESISTANCE gets increased due to which eddy currents produced in copper tube becomes weak. Hence opposing force also gets increased.
Discussion
5128.

The network shown in figure is a part of the circuit. (The battery has negligible resistance) At a certain instant the current I = 2A and it is decreasing at the rate of 10^2 "As"^(-1). What is the potential difference between the points B and A ?

Answer»

8.0 V
8.5 V
10 V
15 V

SOLUTION :`V_A-IR+epsilon-(-L(DI)/(dt))=V_B`
`THEREFORE V_B-V_A=-IR+ epsilon+L(dI)/(dt)`
`=-2xx2+12+5xx10^(-3)xx10^(-2)`
=-4+12+0.5
=8.5 V
Discussion
5129.

A reactive element, in an a.c. circuit, causes the current flowing (i) to lag in phase by pi/2, (ii) to lead in phase by pi/2with respect to the applied voltage. Identify the element in each case.

Answer»

SOLUTION : (i) In an inductor CURRENT lags behind the voltage by a PHASE ANGLE of `pi/2`
(ii) In a capacitor current LEADS the voltage by a phase angle of `pi/2`
Discussion
5130.

If the gravitational force varies inversely as the nth power of the distance then, the time period T of a satellite revolving in a circular orbit round the earth at distance r is proportional to :

Answer»

`( R )^((n+1)/(2))`
`( r )^((n-1)/(2))`
`(1)/(SQRT(r^(n-1)))`
`(1)/(sqrt(r^(n+1)))`

ANSWER :A
Discussion
5131.

A fork gives 5 beats with a 40 cm length of sonometre wire. If the length of the wire is shortened by 1 cm, the number of beats is still the same. The frequency of the fork is :

Answer»

385 Hz
600 Hz
395 Hz
400 Hz

Solution :Here v = `(1)/(2l)sqrt(T//m)`
`THEREFORE "" v l ` = constant
`therefore"" v_(1) l_(1)= v_(2) l_(2) `.
If v be the FREQUENCY of TUNNING fork.
`(v - 5) 40= (v + 5) 39 `.
`rArr "" v = 395 ` Hz.
Hence the correct CHOICE is (c).
Discussion
5132.

A short bar magnet o magnetic field . It experiences a torque of 0.05 J. Calculate the magnitude of the magnetic field.

Answer»

Solution :Theposition of minimum energy corresponds to position of STABLE equilibrium
The energy `(upsilon) = - mB cos THETA `
when `theta = 0^(@) , upsilon = - MU B ` = minimum energyHence when the bar MAGNET is placed parallel to the MAGNETIC field , it is the state of stable equilibrium.
Discussion
5133.

The current in a 90mH inductor changes with time as i=1.0t^2, where I is in amperes and t is in seconds.

Answer»

the MAGNITUDE of the INDUCED emf at t=4.0s is 180 mV
the emf zero at time t=3.0s
the magnitude of the inducedemf at t=4.0s is 360 mV
the emf zero at time t=4.0s

Answer :A::B
Discussion
5134.

How is current kept continous inside a conductor ?

Answer»

SOLUTION :By MAINTAINING a PD. Between the to ENDS of a CONDUCTOR.
Discussion
5135.

It is raining at a speed of 5 ms^(-1) at an angle 37^@ to vertical, towards east. A man is moving to west with a velocity of 5 ms^(-1). The angle with the vertical at which he has to hold the umbrella to protect himself from rain is

Answer»

`TAN^(-1) (2)` to west
`Tan^(-1) (2)` to east
`Tan^(-1) (1//2)` to south
`Tan^(-1) (1//2) ` to east

Answer :A
Discussion
5136.

If a hemispherical body is placed in a uniform electric field E then the flux linked with the curved surface is

Answer»

`2pi R^2 E`
`PI R^2E`
`4 pi R^2 E`
`6 pi R^2 E`

ANSWER :B
Discussion
5137.

A current I is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will stop further accumulation of electrons.

Answer»

SOLUTION :`(IB)/(An E)`
Discussion
5138.

A current I is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n What will be the potential difference developed across the width of the conductor due to the electron accumulation? The appearance of the transverse emf, when a current - carrying wire is placed in a magnetic field, is called Hall effect.

Answer»

SOLUTION :`(IBD)/(An E)`
Discussion
5139.

A bird 'B' in air is diving vertically downwards over a water tank with speed 5 cm/s. Base of thetank is silvered. A fish 'F' in the tank is rising vertically upwards along the same line with speed 2 cm/s. Water level is lowered at the rate of 2 cm/s. Take mu_("water") = 4/3

Answer»


ANSWER :A::B::C::D
Discussion
5140.

A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at 22^@ with the horizontal. The horizontal component of the earth's magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth's magnetic field at the place.

Answer»

Solution :Here angle of dip `delta=22^@ ` and horizontal COMPONENT of earth.s MAGNETIC FIELD `B_H = 0.35 G =0.35 XX 10^(-4) T`
`B_H = B_E cos delta`
`implies` Earth magnetic field `B_E = (B_H)/(cos delta) = (0.35xx10^(-4))/(cos 22^@) = (0.35xx10^(-4))/(0.9272) = 3.8 xx 10^(-5) T ` or0.38 G= `0.35 xx 10^(-4) T`
`B_H = B_E = cos delta`
`implies` Earth.s magneticfield `B_E = (B_H)/(cos delta) =(0.35xx10^(-4))/(0.9272)=3.8xx10^(-5) T ` or 0.38 G.
Discussion
5141.

d/dx (1/x) =?

Answer»

`x^2`
-`x^2`
`1/x^2`
-`1/x^2`

ANSWER :D
Discussion
5142.

Along wire carries a current of 18 A kept along the axis of a long solenoid of radius 1 cm. The field due to the solenoid is 8.0 xx10^(-3)T. The magnitude of the resultant field at a point 0.6 mm from the solenoid axis is (Assume mu_0 = 4pi x 10^(-7)Tm/A)

Answer»

`6 xx 10^(-3)T`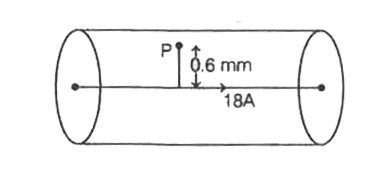
`6 xx 10^(-4) T `
`2 sqrt(7) xx 10^(-3) T`
`10 xx 10^(-3) T`

Solution :GIVEN , current in a long wire ,`I = 18A`

Magnetic field due to a solenoid ,
` B_1 = 8 xx 10^(-3) T`
and r = 0.6 mm ` = 0.6 xx 10^(-3) m`
Radius of solenoid , `R = 1 cm = 1 xx 10^(-2) m `
Magnetic field due to current carrying wire at a point , P
`B_2 = (mu_0)/(2pi) . I/r = 2 xx 10^(-7) xx ( 18)/(0.6 xx 10^(-3) )`
` = 6 xx 10^(-3) T `(in upward direction)
Since, current carrying wire is placed along the axis of solenoid, HENCE magnetic field produced by wire and magnetic field due to solenoid at point P, both are perpendicular to each other, Hence, the magnitude of the resultant magnetic field,
`B = sqrt (B_1^2 + B_2^2)`
` = sqrt ( (8 xx 10^(-3))^2 + (6 xx 10^(-3) )^2 )`
` = 10 xx 10^(-3) T`
Discussion
5143.

A charged sphere of mass m and charge q starts siliding from rest on circular track of radius R from the position shown in the figure. There exists a uniform and constant horizontal magnetic field of induction B . Find the maximum force exerted by the track on the sphere.

Answer»

SOLUTION :`F_m` = qVB (DIRECTED radially outward)
N- mg `sin theta - qvB = (mV^2)/(R)`
`N = (mv^2)/R + mg sin theta + qVB`
`theta = (PI)/(2),`N is maximum.
`N = m/R (2gR) + mg + qB sqrt(2gR)`
`N= 3 mg + qB sqrt(2gR)`
Discussion
5144.

A point object is placed at (0, 0, 0) and a plane mirror is placed parallel to YZ plane at x = 2. Find the coordinate of image

Answer»


ANSWER : (4, 0, 0)
Discussion
5145.

If alpha,beta,gama are the zeros of the polynomial x^3-6x^2-x+30 then (alpha.beta + beta.gama + gama.alpha) = ?

Answer»

-1
1
-5
30

Answer :A
Discussion
5146.

If sky wave with a frequency of 60 MHz is incident on D-region at angle of 30^(@), then the angle of refraction.

Answer»

`30^(@)`
`60^(@)`
`45^(@)`
`90^(@)`

ANSWER :A
Discussion
5147.

.......... Suggested that earth behaves as a giant bar magnet

Answer»


ANSWER :GILBERT
Discussion
5148.

In the circuit shown in figure, epsilon_(1) =3 V,epsilon_(2) = 2 V , epsilon_(3) = IVandR = r_(1) = r_(2) = r_(3)= 1 Omega . The current through each branch is...... and potential difference between the points A and B is .......

Answer»

Solution :Let `I_(1) ,I_(2) and I_(3)` be the currents through the resistors `r_(1), r_(2) and r_(3)`respectively as indicated in figure. USING Kirchoff.s second RULE to loops abaca and abcdefa we have,
`I_(1) r_(1) - epsilon_(1) + epsilon_(2) + I_(2) r_(2) = 0 ""` ..... (1)
`I_(1) r_(1) - epsilon_(1) + epsilon_(3)+ I_(3)r_(3) = 0""` ..... (2)
From equation (1) and (2),
`epsilon_(1) - I_(1) r_(1) = epsilon_(2) + I_(2) r_(2) = epsilon_(3) + I_(3) r_(3) ""` .... (3)
Applying Kirchoff.s first rule to junction a, we have `I_(1)= I_(1) + I_(3) "" ` .... (4)
Using equation (4) in (3) , we get ,
` epsilon_(1) - (I_(2) + I_(3) ) r_(1) = epsilon_(3) + I_(3) r_(3)`
or, `2I_(3) + I_(2) = 2"" `.... (5)
Also `epsilon_(2) +I_(2) r_(2) = epsilon_(3) + I_(3) r_(3)`
or , `I_(3) - I_(2) = I "" ` .... (6)
From equation (4) , (5) and (6) ,
`I_(1)= IA, I_(2) = 0 A and I_(3) = 1 A `
Potential difference between A and B
= Potential difference between a and d
= `epsilon_(1) - I_(1) r_(1) = 3 -1 XX 1 = 2 ` V
Discussion
5149.

An inductor of unknown value, a capacitor of 100 uF and a resistor of 10 Omega are connected in series to a 200 V, 50 Hz a.c. source. It is found that the power factor of the circuit is unity. Calculate the inductance of the inductor and the current amplitude.

Answer»

SOLUTION :Here `C = 100 muF = 10^(-4) F, R = 10 OMEGA, V_(rms) = 200 V` and v= 50 HZ
As the power factor is unity hence, `X_(L) = X_(C)` or `Lomega = 1/(C omega)`
`therefore L = 1/(C omega) = 1/(C.4pi^(2) v^(2)) - 1/(10^(-4) XX 4 xx (3.14)^(2) xx (50)^(2)) = 0.1 H`
Current amplitude `I_(m) = (sqrt(2)V_(rms))/R = (sqrt(2) xx 200)/10 = 28.2 A`
Discussion
5150.

Weights of 1g, 2g,...., 100g are suspended from the 1-cm, 2-cm,......, 100-cm marks respectively of a light meter scale. Where should it be supported for the system to be in equilibrium ?

Answer»

55-cm MARK
60-cm mark
66-cm mark
72-cm mark

Answer :C
Discussion