Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

6751.

An electicdipoleplacedin vacuumis formedby twoequalbutopposite charges each of magnitude1mu Cseparatedby a distance of 2 cm. calculatethe electric fieldintensities in thefollowingcases :(i)ata pointon theaxisof thedipole situatedata distance60 cmaway from itscentre. (ii)ata pointon theperpendicularbisector ofthedipolesituatedat a distance60cmawayfrom itscentre.

Answer»

SOLUTION :Moment of the electricdipole,
` p = q * 2l = 1 xx 10 ^(-6)xx 2 xx 10 ^( -2 )= 2 xx10^(- 8 ) C *m `
(i) Electricfieldintensity on theaxisof the dipole,
`E _ 1=( 1 ) /( 4piin _0)*( 2p ) /( R ^ 3 )=( 9 xx 10 ^ 9xx 2 xx 2 xx 10 ^( - 8)) /( (0 .6) ^3 ) `
` = 1666.6 N *C^( -1 )` ,ALONGTHE axis
(ii)Electricfieldintensity on the perpendicularbisector of the dipole,
`E _ 2=( 1 ) /( 4pi in _0 )* (p ) /(r ^ 3)=( 1 )/( 2 )E _ 1 `
` = 833.3 N*C ^ (-1 )` ,parallelto axisof thedipole
Discussion
6752.

A charge 'q' is enclosed in a cube. What is the electric flux associated with one of the faces of the cube ?

Answer»

`epsilon_0/Q`
`q/epsilon_0`
`(6Q)/epsilon_0`
`q/(6epsilon_0)`

ANSWER :D
Discussion
6753.

At time t= 0 , number of nuclei of a radioactive substance is 100. At t = 1 s this number becomes 90. Find the number of nuclei at t = 2s.

Answer»

SOLUTION :In 1 second 90% of the NUCLEI have remained undecayed, so in ANOTHER 1 second 90% of 90 i.e., 81 nuclei will REMAIN undecayed.
Discussion
6754.

The width of fringes ...... as the Young's double slit experiment moves from air to water

Answer»

becomes infinite
DECREASES
increacses
does not change

Solution :Width of slit `(2barX) PROP lambda`, experiment done from air to water, wavelength of LIGHT decreases HENCE width of fringes also decreases.
Discussion
6755.

A diverging beam of rays from a point source S , making a divergent angle , alpha are incident on a glass slab (as shown in Fig. 2.82). The angle of incidence of the extreme rays on the two sides is the same. If thickness of the glass slab is t and refractive index n, then the angle of divergence of the emergent rays will be

Answer»

ZERO
`-alpha`
`sin^(-1)(1)/(n)`
`2SIN^(-1)(1)/(n)`

ANSWER :B
Discussion
6756.

A particle of mass 5 kg is moving along a circular path of radius 1 m. It is making 300 rp., uniformly. Its kinetic energy would be:

Answer»

100 `pi^2` J
50 `pi^2` J
250 `pi^2` J
zero

Solution :Here the `E_k=1//2 m v^2`
or`E_k=1/2mr^2omega^2=(mr^2(2pin)^2)/(2)`
=`1/2xxmr^2xx4 pi^2.n^2`
=`2M r^2 pi^2.n^2`
=`2xx5xx(1)^2pi^2xx(300/60)^2`
=`10pi^2xx25=250 pi^2J`
Discussion
6757.

A coil of surface area 200 cm^2 having 25 turns is held perpendicular to the magnetic field of intensity 0.02 "Wb/m"^2. The resistance of the coil is 1Omega if it is removed from the magnetic field in 1s, the induced charge in the coil is ….. C.

Answer»

1
0.01
0.1
0.001

Solution :`Q=N (Deltaphi)/R` but `Deltaphi=AB-0=AB`
`THEREFORE Q=(NAB)/R`
`=(25xx200xx10^(-4)xx0.02)/1`
`=100xx10^(-4)` =0.01 C
Discussion
6758.

The phase difference between the voltage and the current in an A.C. circuit is pi/4. If the frequency is 50 Hz, then this phase difference is equivalent to a time of :

Answer»

0.05 s
2.5 m s
25 ms
0.25 s

Answer :B
Discussion
6759.

A block of mass M_(1) and a block of mass M_(2) are connected by a string that passes over a pulley as shown in Fig. The pulley is a uniform disk of radius R and mass M. Find the acceleration of the two object, using the concepts of angular momentum and torque.

Answer»

Solution :(1) If the block `M_(1)` moves upward, the block `M_(2)` moves DOWNWARD, and the pulley will rotate counterclockwise. This problem is same as Sample Problem we have already solved, except that now we have to use angular momentum and torque to find acceleration.
(2) We define the blocks and pulley as our system. We consider the AXLE of the pulley as our axis. We can write the angular momentum of the system considering the ball and the block that are moving translationally and the pulley which is UNDERGOING pure rotation. The external torque on the system about the axis is due to the weights of the blocks.
Calculations: Due to constraint, the blocks have same speed n. We can find angular momentum using the definition of angular momentum about the axle, given by equation `vecL=vecrxxvecp`.
The momentum and position vectors are given by
`vecP_(1)=-M_(1)nuhatjandr_(1)=-Rhati-y_(1)hatj`
Using `vecL=vecrxxvecp`, the angular momentum of block 1 is `M_(1)nuRhatk`.
Similarly, for block 2, momentum and position vectors are given by
`vecP_(2)=+M_(2)nuhatjandr_(1)=Rhati+y_(2)hatj`
Using `vecL=vecrxxvecp`, the angular momentum of block 2 is `M_(2)nuRhatk` about our chosen axis.
The angular momentum of the pulley can be found using `L=Iomega`. It is given by `M_(p)R^(2)omegahatk//2` about our chosen axis.
We calculate the external torque acting on the system about the pulley axle. The force is being exerted by the axle on the pulley, but it does not produce torque about the axle as the LENGTH of moment arm is zero.
The gravitational force `M_(1)vecg` acting on block 1 PRODUCES a torque about the axle equal to `M_(1)gRhatk` and the gravitational force `M_(2)vecg` acting on block 2 produces a torque about the axle equal in magnitude to `-M_(2)gRhatk`, where R is the moment arm of the force about the axle. Thus, the total external torque about the pulley axle is
`sumtau_(ext)=M_(1)gRhatk-M_(2)gRhatk`
Writing an expression for the total angular momentum of the system,
`L=(M_(1)nuR+M_(2)nuR+MnuR)hatk`
Substituting this expression and the total external torque in
`sumt_(ext)=(dL)/(dt)`
`M_(1)gRhatk-M_(2)gRhatk=d/dt[(M_(1)+M_(2)+M)nuR]hatk`
`M_(1)gR-M_(2)gR=(M_(1)+M_(2)+M)R(dnu)/(dt)`
Recognizing that `dnu//dt=a` and solving Eq. for a
`a=((M_(1)-M_(2))g)/(M_(1)+M_(2)+M)`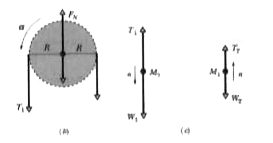
Discussion
6760.

Electric field 'E' at a point situated at a normal distacne 'r' from an infinitely long uniformaly charged straight were is proportional to

Answer»

`E infty R`
` E PROP (1)/® `
` Eprop (1)/(r^(2))`
` E prop (1)/(r^(3))`

Answer :B
Discussion
6761.

Who is the writer of the poem?

Answer»

GARETH Owen
Sirpheno The Knight
John Keats
None of the above

Answer :A
Discussion
6762.

Which of the following animal struts?

Answer»

Duck
Horse
Cock
Cat

Answer :C
Discussion
6763.

The anode plate in an experiment on photoelectric effect is kept vertically above the emitter plate. Light source is put on.An electric field is switched on which has vertically downward direction.

Answer»

The PHOTOCURRENT will increase
The kinetic energy of the ELECTRONS will increase
The stopping POTENTIAL will decrease
The transhold WAVELENGTH will increase

Answer :B
Discussion
6764.

In order to heat a liquid an electric heating coil is connected is to a cell of emf E = 12 V and internal resistance r = 1 Omega. There are three options for selecting the resistance (R) of the heating coil. R can be chosen as 1 Omega, 2 Omega or 4 Omega. The cell has a rating of 2000 mAh (milli Ampere hour) and it is to be used to heat the liquid till it expires. [The cell maintains constant emf till it lasts] (a) Which value of R will you chose so that maximum heat (H_0) is transferred to the liquid before the cell expires? Calculate H_(0). (b) Which value of R will chose so that heat is transferred to the liquid at fastest possible rate? What percentage of H_(0) (as obtained in (a)) is transferred to the liquid in this case by the time the cell expires ?

Answer»


ANSWER :(a) `4 Omega,69.12 KJ`
(B) `1 Omega,62.5 %`
Discussion
6765.

A rectangular tank of mass m_(0) and charge Q over it is placed over a smooth horizontal floor. A horizontal electric field E exist in the region. Rain drops are falling vertically in the tank at the constant rate of n drops per second. Mass of drops is m. Find the time in second taken by tank to reach to half the maximum speed. (given m_(0)=30kg, m=1mg and n=10^(4))

Answer»

Solution :Mass oftank at time `t`
`M=m_(0)+nmt`
Let VELOCITY of TANK be `v`
`M(dv)/(DT)=QE-vnm`
For `v_(max)`, `(dv)/(dt)=0`
`RARR v_(max)=(QE)/(nm)`
from `(i)`
`(m_(0)+nmt)(dv)/(dt)=QE-vnm`
`rArrint_(0)^(v)(dv)/(QE-vnm)=int_(0)^(t)(dt)/(m_(0)+nmt)`
` rArr-(1)/(nm)[LN(QE-nmv)]_(0)^(v)=(1)/(nm)[ln(m_(0)+nmt)]_(0)^(t)`
`rArr ln((QE-nmv)/(QE))=-ln((m_(0)+nmt)/(m_(0)))`
` rArr(QE-nmv)/(QE)=(m_(0))/(m_(0)+nmv)`
`rArr1-(nmv)/(QE)=(m_(0))/(m_(0)+nmt)`
`rArr(nmv)/(QE)=1-(m_(0))/(m_(0)+nmt)=(nmt)/(m_(0)+nmt)`
`rArrt=(m_(0))/((QE)/(v)-nm)`
required time when `v=v_(max)//2=(m_(0))/((2QE)/(v_(max))-nm)=(m_(0))/(nm)`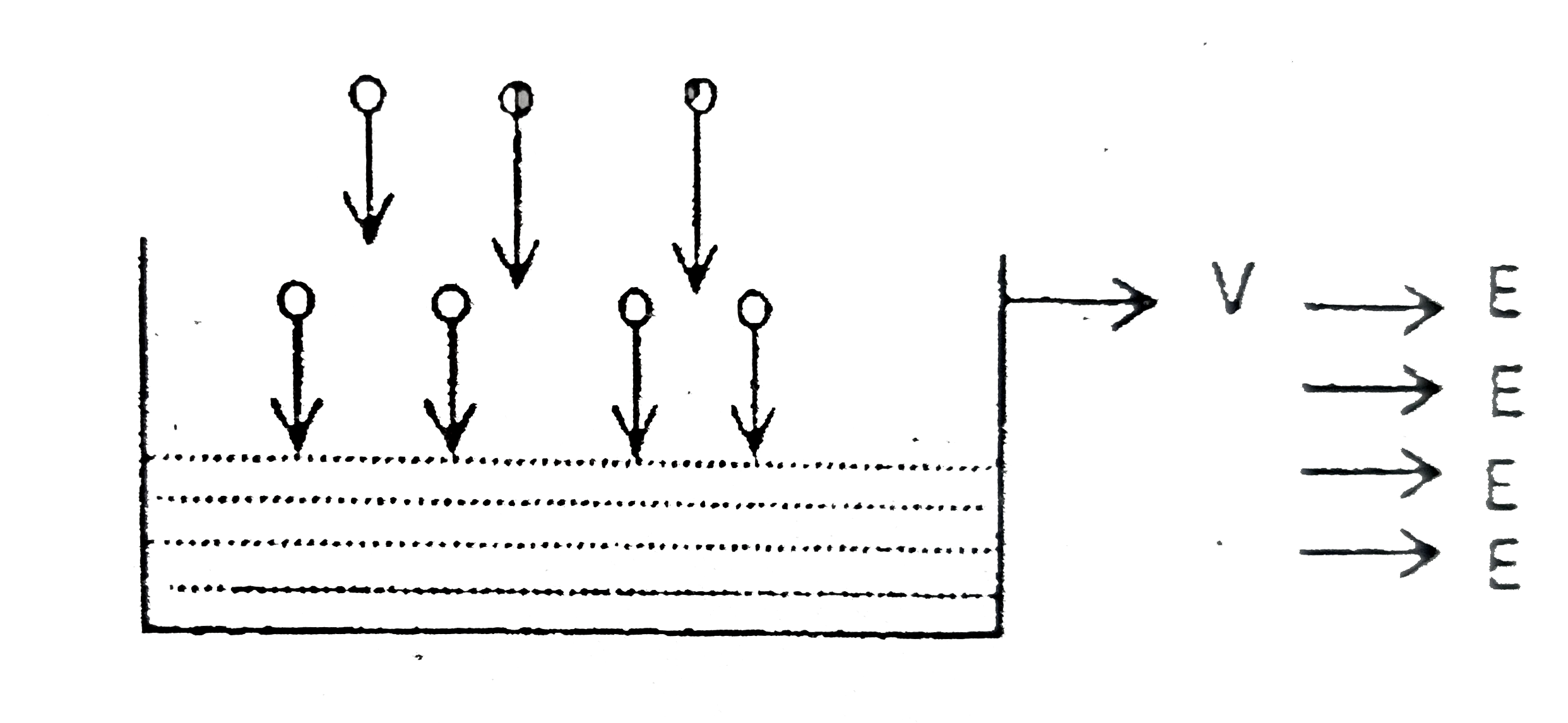
Discussion
6766.

Polarized light

Answer»

Is a DIFFERENT form of LIGHT
Can show interference pattern
Travels in any medium with a velocity slightly more than that for UNPOLARIZED light
Has direction of VIBRATION restricted in some way

Answer :D
Discussion
6767.

A circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switchdisconnected, the capacitor was charged to a voltage V_(0), and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is I_(max) equal to ?

Answer»

Solution :`o=(q)/(C)+L(dI)/(dt)+RI, I=+(dq)/(dt)`
For the critical case `R=2sqrt((L)/(C))`
Thus `LCddot(q)+2 sqrt(LC)dot(q)+q=0`
Look for a solution with `q prop E^(alphat)`
`alpha=-(1)/(sqrt(LC))`
An independent solution is `t e ^( alpha t)`. Thus
`q=(A+Bt)e^(-t//sqrt(LC))`,
At `t=0 q=CV_(0) ` thus `A=CV_(0)`
Also at`t=0 dot(q)=I=0`
`0=B-A(1)/(sqrt(lC))implies B=B_(0)sqrt((C)/(L))`
Thus FINALLY `I=(dq)/(dt)=V_(0)sqrt((C)/(L))e^(-t//sqrt(LC))`
`-(1)/(sqrt(LC))(CV_(0)+V_(0)sqrt((C)/( L))t) E^(-t//sqrt(LC))`
`=-(V_(0))/( L)te^(-t//sqrt(LC))`
The current has been defined to increase the CHARGE. Hence the MINUS sign. ltbr. The current is maximum when
`(dI)/( dt)=-(V_(0))/(L) e^(-t//sqrt(LC))(1-(t)/(sqrt(LC)))=0`
This GIVES `t= sqrt(LC)` and the magnitude of the maximum current is
`|I_(max)|=(V_(0))/(e)sqrt((C)/(L))`.
Discussion
6768.

The transmitting antenna of TV station is 300 m high. Find the area of the earth's surface in which TV signals can be received from it.(Radius of the earth = 6400 km).

Answer»

Solution :AREA over which SIGNALS can be received, A = `pid^2`
Where d=sqrt(2Rh), R being the radius of the earth and h the height of the transmitting ANTENNA.
`thereforeA=pixx2Rh=2piRh`
`=2xx3.14xx6.4xx10^6xx300`
`=12.058xx10^9m^2=12058km^2`
Discussion
6769.

Electric field in a region is given by vec( E) = - 4xhat(i) + 6yhat(j). Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram

Answer»

`epsilon_(0)`
`2 epsilon_(0)`
`3 epsilon_(0)`
`10 epsilon_(0)`

Answer :B
Discussion
6770.

A 30 kg block is to be moved up an inclined plane at an anglue 30° to the horizontal with a velocity of 5ms^(-1). If the frictional force retarding the motion is 150N find the horizontal force required to move the block up the plane. (g=10ms^(-2))

Answer»

Solution :The FORCE required to a body up an inclined plane is:
`F = mg sin theta +` FRICTIONAL force.
`=30(10) sin 30^(@) + 150 = 300 N`
If P is the HORIZONTAL force, `F = P cos theta`
`P = F/(cos theta) = 300/(cos theta) = (300 xx 2)/sqrt(3) = 200sqrt(3) = 346 N`
Discussion
6771.

One milliwatt of light of wavelength 4560Å is incident on a cesium surface. Calculate the photoelectric current liberated, assuming a quantum efficiency of 0.5%. Given work function for cesium = 1.93 eV :

Answer»

1.856 mA
`1.856muA`
`18.56muA`
none of these.

Solution :ENERGY of each photon of incidentlight is
`E=HV=(hv)/(lambda)=(6.62xx10^(-34)xx3xx10^(8))/(4560xx10^(-10))`
`=4.32xx10^(-19)J`
Power of source `=10^(3)W(=P)`
NUMBER of photons liberarted per sec.
`N=(P)/(E)=(10^(-3))/(4.32xx10^(-19))=2.32xx10^(15)` per sec.
As quantum efficiency is `0.5%` of EFFECTIVE number of incident photons is only `0.5%` which ejecte photoelectron.
`:.` Number of electrons ejected as
`N_(e)= 2.32xx10^(15)xx(0.5)/(100)=1.16xx10^(13)//sec`
`:.` CORRESPONDING photo electric current proudced,
`i=(q)/(t)=(n.N_(e))/(t)=1.6xx10^(-19)xx1.16xx10^(13)`
`=1.856xx10^(-6)A`
`u=1.856 muA`.
Discussion
6772.

Define intensity of radiation on the basis of photon picture of light. Write its S.I. unit.

Answer»

SOLUTION :The amount of LIGHT `"ENERGY" // "Photon"` energy, incident per metre square per second is called intensity of `"JOULE" // "Sec-metre"^(2)` radiation.
SI Unit : `W // m` or `"Joule" // "Sec-metre"^(2)`).
Discussion
6773.

Assertion:A free neutron is unstable Reason : Free neutron disintegrates into proton, electron and an antineutrino i.e. n to p + e^(-) + barupsilon

Answer»

If both assertion and REASON are TRUE and reason is the correct explanation of assertion .
If both assertion and reason are true but reason is notthe correct explanation of assertion .
If assertion is true but reason is false .
If both assertion and reason are false

ANSWER :a
Discussion
6774.

A block of mass 2 kg is moving with a velocity of 2hati-hatj+3hatk m/s. Find the magnitudeand direction of momentum of the block with the x-axis.

Answer»

Solution :The magnitude of MOMENTUM is `2sqrt(14)kg` m/s and the direction is at an angle of `TAN^(-1)( SQRT((2)/(7)))` with x-axis.
Discussion
6775.

If on the x - axis electric potential decreases uniform from 60 V to 20 V between x = -2 m to x = +2 m then the magnitude of electric field at the origin

Answer»

Must be 10 V/m
MAY be greater than 10 V/m
is ZERO
is 5 V/m

Answer :B
Discussion
6776.

A ball falls on the surface from 10 m height and rebounds to 2.5 m. If the duration of contact with the floor is 0.01 sec. Then average acceleration during contact is:

Answer»

2100 `MS^(-2)`
1400 `ms^(-2)`
700 `ms^(-2)`
400 `ms^(-2)`

Solution :Here `a=(V_2-V_1)/(t)`
Now `v_2=SQRT(2gh_2)=sqrt(2xx10xx2.5)=sqrt(50)`
and `v_1=sqrt(2xx10xx10)=sqrt(200)`
`:. (sqrt(200)-sqrt(50))/(0.01)=a`
or a=2100 `ms^(-2)`
Discussion
6777.

Match the following{:("List - I ","List - II "),("a)cigerent monochromatic highly unidirectionally","e)Malus law "),("b) " I = I_(0) cos^(2)theta,"f)Polstiod "),("c) Selective absorption is exhibited by ","g) Spherical wave front "),("d) Fresnel diffraction","h) LASER "):}

Answer»

`a - H, B - e, C - F, d - g`
`a - g , b - h, c - e, d - f`
`a - h, b - g, c - e, d - f`
`a - g, b - h, c - f, d - e`

Answer :A
Discussion
6778.

Consider an interference pattern between two coherent sources.If I_1 and I_2be intensities at pointswhere the phase difference are pi/3 and (2pi)/3and respectively , then the intensity at maxima is

Answer»

`(I_2 - 3I_1)/(2)`
`(I_1 - 3I_2)/(2)`
`(3I_2 + I_1)/(2)`
`(3I_1 - I_2)/(2)`

ANSWER :D
Discussion
6779.

A parabolic section of wire, as shown in figure is located in the X-Y plane and carries a current of 12A. A uniform magnetic field B = 0.4T making an angle of 60 with X-axis exists throughout the plane. The total force acting on a wire between the origin and the point X=0.25m, y = 1.00 m.

Answer»

`0.68 HATK N`
`-0.68hatk N`
`1.36hatk N`
`-1.36hatk N`

ANSWER :D
Discussion
6780.

An ionized H-molecule consists of an electron and two protons. The protons areseparated by a small the ground state distance of the order of angstrom. In the ground state (a) The electron would not move in circular orbits The energy would be (b) times that of a H-atom (c) The electrons orbit would go around the protons (d) The molecule will soon decay in a proton and a H-atom

Answer»

B' and 'd' are TRUE
a' and 'b' are true
a' and 'c' are true
b' and 'c' are true

Answer :C
Discussion
6781.

If the incidentwavelength on a photodiode is 1700 nm, what is its energy gap (E_(g)) ?

Answer»

0.073 eV
1.20 eV
0.73 eV
1.16 eV

Solution :0.73 eV
`E_(G)=(hc)/(LAMBDA)`
`=(6.62xx10^(-34)xx3xx10^(8))/(17xx10^(-7)xx1.6xx10^(-19))=0.73014~~0.73eV`
Discussion
6782.

How does the de-Broglie wavelength of a charged particle changes when accelerating potential increases ?

Answer»

Solution :The de-Broglie WAVELENGTH DECREASES when ACCELERATING potential increases. (since `LAMBDA prop =(1)/(sqrtV)`)
Discussion
6783.

Time of flight is given by t=((-))/g.

Answer»


ANSWER :`[U SING THETA]`
Discussion
6784.

Which of the following is not the unit of magnetic induction ?

Answer»

tesla
gauss
oersted
`Wb/m^2`

ANSWER :C
Discussion
6785.

A uniform circular ring of radius R, mass m has uniformly distributed charge q. The ring is force to rotate about its own axis (which is vertical) without friction. In the space a uniform magnetic field B, directed vertically down ward exists in a cylindrical region. The cylindrical region is co-axial with B and has a radius greater than R. If B increasesa at a constant rate (dB)/(dt)=alpha. angular acceleration of the ring will.

Answer»

DIRECTLY PROPORTIONAL to R
Directly proportional to q
Directly proportional to m
Independent of R and m

Answer :B
Discussion
6786.

A slit of width 'd' is placed infront of a lens of focal length 0.5 m and is illuminated normally with light of wavelength 5.89 xx 10^(-7)m . The first diffraction minima on either side of the central diffraction maximum are separated by 2xx10^(-3). Find the width of the slit.

Answer»

SOLUTION : 0.294mm
Discussion
6787.

Answer the following questions: (ii) Why are infrared waves referred to as heat waves ? How are they produced ? What role do they play in maintaining the earth.s warmth through the green house effect ?

Answer»

Solution :(ii) Infrared rays are referred as heat waves because water molecules present in most MATERIALS readilyabsorb infrared waves and are HEATED up. Infrared waves are produced by hot bodies and molecules. These radiation plays an IMPORTANT role in maintaining the earth.s warmth through the greenhouse EFFECT.
Discussion
6788.

Explain the use of potentiometer for comparison of e.m.f. of two cells.

Answer»

Solution :Potentiomter. A potentiomter consists of a uniform and long wire stretched on a wooden board. Its ENDS are connected to battery B through rheostat `R_(h) and ` an ammter. Ells whose e.m.f.s are to be compared are connected as shown in the FIGURE.
Priciple. the potential drop across any PORTION of the wire, is directly proporrtional to the length of that portion of wire, provided wire is uniform and a constant current flows through it.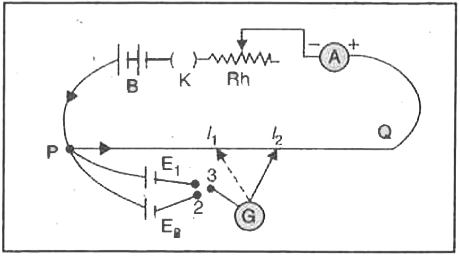

Comparison of e.m.f..s of two cells. The positive of `E_(1) and E_(2)` are connected to a terminal P where the positive of auxiliary battery B is connected. negative are connected to a galvanometer through two way key. the other end of galvanometer is connected to a jockey which can slide over the wire. circuit is closed FIRST by putting the key between 1,3 and then between 2,3. the length of the wires, `l_(1) and l_(2)` for which there is no deflection in the galvanomter is noted.
Now `E_(1) prop l_(1) and E_(2) propl_(2)`
or `E_(1)=kl_(1) and E_(2)=kl_(2)`
Dividing, `(E_(1))/(E_(2))=(l_(1))/(l_(2))`
Discussion
6789.

Statement I: In fission reaction : ""_(92)P^(263) to Q^(141)+""_(36)R^(10)+3_(0)n'. The values of a = 56 and b = 119. Statement II: The electrons emitted in beta-decay have same energy.

Answer»

A STATEMENT I is TRUE, statement II is false.
Statement I is false, statement II is true.
C Statement I is true, statement II is true, Statement II is correct EXPLANATION of statement I.
Statement I is true, statement II is true and statement I is not correct explanation of statement II.

Answer :A
Discussion
6790.

What is the equivalent capacitance, C of the five capacitors connected in figure below.

Answer»


ANSWER :`C=C_3,` because the COMBINATIONS of `C_1` and `C_2` as WELL as `C_4` and `C_5` have been SHORTED.
Discussion
6791.

540 gm if ice at 0^@C is mixed with 540 gram of water at 80^@C . The final temperature of the mixture is

Answer»

`0^@C`
`40^@C`
`80^@C`
LESS than `0^@C` .

ANSWER :A
Discussion
6792.

The maximum speed of a particle executing an S.H.M. is 1" m s"^(-1) and maximum acceleration is 1.57" m s"^(-2). The timeperiod of S.H.M. is :

Answer»

0.25 s
4.00 s
1.57 s
`(1)/(1.57)s.`

Solution :`v_("MAX")=r omega` and `a_("max")=omega^(2)r`.
`(a_("max"))/(v_("max"))=omega=(2PI)/(T)`
`T=2pi""(v_("max"))/(a_("max"))=2pi.(1)/(157)=4` s.
Hence correctchoice is (b).
Discussion
6793.

Values of mu_(r ) and in_(0) are respectively 2 NA^(-2) and 8C^(2)N^(-1)m^(-2), then speed of light is ….

Answer»

`0.25`
`0.5`
`0.75`
`1.0`

SOLUTION :`c=(1)/(sqrt(mu_(0)in_(0)))=(1)/(sqrt(2xx8))=(1)/(4)`
`therefore c=0.25 MS^(-1)`
Discussion
6794.

When accelerated along a straight line at 2.8xx10^(15)m//s^(2) in a machine, an electron ( mass m=9.1xx10^(-31)kg) has an initial speed of 1.4xx10^(7) m/s and travels 5.8 cm. Find (a) the final speed of the electron and (b) the increase in its kinetic energy.

Answer»


ANSWER :(a) `2.3xx10^(7)m//s; (B) 1.5xx10^(-16)J`
Discussion
6795.

The number of silicon atoms per m^(3) is 5xx10^(28). This is doped simultaneously with 5xx10^(22) atoms per m^(3) of Arsenic and 5xx10^(20) per m^(3) atoms of Indium. Calculate the number of electrons and holes. Given that n_(i)=1.5xx10^(16)m^(-3). Is the material n-type or p-type?

Answer»

SOLUTION :Here number of atoms of Arsenic per `m^(3)` is,
`N_(D)=5xx10^(22)`
and number of atoms of Indium per `m^(3)` is,
`N_(A)=5xx10^(20)`
`therefore` Number of electrons per `m^(3)`,
`n_(e )=N_(D)-N_(A)=(5xx10^(22)-0.05xx10^(22))`
`=4.95xx10^(22)`
but `n_(i)^(2)=n_(e )n_(h)`
`therefore n_(h)=(n_(i)^(2))/(n_(e ))=((1.5xx10^(16))^(2))/(4.95xx10^(22))`
`thereforen_(h)=0.4545xx10^(10)`
`~~0.45xx10^(10)`
`~~4.5xx10^(9)m^(-3)`
Here `n_(e ) GT gt n_(h)` so semiconductor is n-type.
Discussion
6796.

Which is the correct phasor diagram for an a.c. circuit containing only a pure capacitor?

Answer»




SOLUTION :The CURRENT LEADS the VOLTAGE by `90^(@)`. (c).
Discussion
6797.

Ultrasonic and Infrasonic Waves: The sound having frequency 20 Hz to 20 KHz is called audible sound Human ear cannot hear sound of frequencies lying outside this range. The limits of audibility of sound vary from individual. Generally the upper limit decreases with increase of age of individual, usually and people can not hear sound of frequency more than 15 kHz. Sound of frequencies below 20 Hz are called infrasonics, while frequencies beyond 20 kHz are called ultrasonics. Ultrasonics can be heard by dogs, cat bats etc. Bats detect the path by means of ultrasonics. Ultrasonics can be used for diagnosis of tumour and other abnormalities within our body. This is known as ultrasonography. Ultrasonics are used to curve various diseases and to measure depth of oceans to detect submarines.

Answer»

BATS only
HUMAN BEINGS only
bats and human beings
neither bats nor human beings

Answer :C
Discussion
6798.

Capacitance of network is

Answer»

Solution :
`IMPLIES C_(AB) =(C )/(3)+C=(4C)/(3)`
Discussion
6799.

A 10 N force is applied on a body produces an acceleration of 1 m//s^(2) . The mass of the body is

Answer»

5 kg
10 kg
15 kg
20 kg

Answer :B
Discussion
6800.

If water drops are falling at regular time intervals from ceiling of height H, then position of drop from the ceiling is (when n^(th) drop falling from the ceiling and r^(th) drop is in its way)

Answer»

`((n-1)^2)/((n-r)^2) H`
`((n-r)^2)/((n-1)^2) H`
`((n-r)^2)/((n+1)^2) H`
`((n+1)^2)/((n+r)^2) H`

ANSWER :B
Discussion