Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3651. |
A stone dropped from the top of a tower of travel 5/9th of the height of the tower during the last second of its fall . The time of fall is. |
|
Answer» 2s |
|
| 3652. |
An astronomical telescope of ten fild angular magnification has a length of 44 cm. The focal length of the object is |
|
Answer» 4 cm |
|
| 3653. |
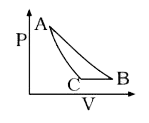
A thermodynamic process is shown in the figure. The pressure and volumes corresponding to some points in the figure are |
|
Answer» `p_(A) = 3 XX 10^(4)` PA, |
|
| 3654. |
Shown below is an experemental set up with a semiconductor diode. |
|
Answer» IDENTIFY the experiment |
|
| 3655. |
The initital speed of an arrow shot from s bow, at an elevation of30^(@) , is15 m s^(-1) , Find the velocity when it hits the ground back. |
|
Answer» Solution :Here ` v_(0) 15 " m s"^(-1)`, angle of projection , ` theta_(0) = 30^(@)` Therefore, ` v_(0x) = v_(0_ cos theta_(0)` ` = 15 cos(30 ^(@))` ` = ( 15 sqrt3)/2 " m s"^(-1)` And ` v_(0y) = v_(0)sin theta_(0)` ` = 15/2 m s ^(-1)` Horizontal component of velocity remians CONSTANT throughout the fight i.e. ` v_(x) = v_(0x) = (15 sqrt3)/2ms^(-1)` Vertical component of velocity is given by ` v_(y) = v_(0) sin theta_(0) - GT ` Put` t= T_(f) = ( 2v_(0) sin theta_(0))/g` ` Rightarrowv_(y) = v_(0) sin theta_(0)-g xx ( 2v_(0) sin theta_(0))/ g` ` v_(y) = - v_(0) sintheta_(0)` `1 v_(y) - 15/2m s^(-1)` Thus, total velocity` V = sqrt(v_(x)^(2) + v_(y)^(2))` ` sqrt( ( 15^(2)xx 3)/4+ 15^(2)/4))` `v = 15 m s ^(-1)` Let the final velocity make and angle ` theta` with the positive x - axis , then ` tetha= TAN^(-1) (v_(y)/v_(x))` ` theta = tan^(-1) (((-15)/2)/(15 sqrt3/2))` `= tan^(-1) ((-1)/sqrt3)` ` theta = - 30^(@)` ` (##AAK_T1_PHY_C02_SLV_029_S01.png" width="80%"> |
|
| 3656. |
A wave traveling along a string is described by y(x,t)=(0.00327 m) sin(72.1x - 2.721). (16-21) in which the numerical constants are in SI units (72.1 rad/m and 2.72 rad/s) (a) What is the velocity of this wave? (b) What is the displacement y at x= 22.5 cm and t=18.9s? (c) What is the transverse velocity u of the string element at x =22.5 cm at time t= 18.9s? (This velocity, which is associated with the transverse oscillation of a string elenient, is parallel to the y axis. Do not confuse it with the constant velocity at which the wave form moves along the x axis.) (d) What is the transverse acceleration of our string element at 18.9 3? |
|
Answer» Solution :The speed of the wave is given by Eq. 16-14. `(dx)/(dt)=v=omega/k` Calculation: The speed of the wave is `v=omega/k=(2.72"rad//s")/("72.1 rad//m")=0.0377 m//s` =3.77 cm/s Because the phase in Eq. 16-21 CONTAINS the position varible x the wave is MOVING along the x axis. Also, because the wave equation is written in the form of Eq. 16-4, the minus sign in front of the wt term indicates that the wave is moving in the positive direction of the x axis. Calculations: Equation 16-21 GIVES the displacement as a function of position x and time 1. Substituting the given values into the equation yields `y=0.00327 sin (72.1 xx 0.225 -2.72 xx 18.9)` `=(0.00327 m) sin (-35.1855 rad)` =(0.00327 m) (0.588) =0.00192m =1.92 mm Thus, the displacement is positive. The transverse velocity u is the rate at which at displacement y of the element is CHANGING. In general, that displacement is given by `y(x,t) =y_(m) sin(kx-omegat)`. For an element at a certain location, we find the rate of change of y by taking the derivative of Eq. 16-21 with respect to i while treating x as a constant. A derivative taken while one (or more) of the variables is treated as a constant is called a partial derivative and is represented by a symbol such as `delta//delta t` a rather than d/dt. Calculations: Here we have `u=(delta y)/(delta t)=-omega y_(m) (kx-omegat)` Next, substituting numerical values but suppressing the units, which are SI, we write `u=(-2.72) (0.00327) cos [(72.1) (0.225)-(2.72) (18.9)]` =0.00720 m/s=7.20 mm/s. Thus, at t=18.9 s out string element is moving in the positive direction of y with a speed of 7.20 mm/s. (Caution: In evaluating the cosine function, we keep all the significant figures in the argument or the calculation can be off considerably. For example, round off the numbers to TWO significant figures and then see what you get for u.) (d) The transverse acceleration is the rate all which the element.s transverse velocity is changing Calculations: From Eq. 16-23. again treating as constant but allowing a to vary, we find `a_y=(delta u)/(delta t)=-omega^(2) y_(m) sin (kx-omegat)` Substituting numerical values suppressing the units, which are SI, we have `a_(y)=-(2.72)^(2) (0.03327) sin [(72.1) (0.225) -(2.72) (18.9)]` `=-0.0142 m//s^2)=-14.2 mm//s^(2)` From part (a) we learn that at t=18.9s our string element in moving in the positive direction of y, and here we learn that it is slowing because its acceleration is in the opposite direction of u. |
|
| 3657. |
An ammeter, suspected to give inaccurate reading, is connected in series with a silver voltameter. The ammeter indicates 0.54 A . A steady current passed for one hour deposits 2.0124 gm of silver . If the E.C.E . of silver is 1.118xx10^(-3) gmC^(-1),then the error in ammeter reading is |
|
Answer» `+0.04 A` |
|
| 3658. |
An uncharged capacitor is fully charged with a battery . The ratio of energy stored in the capacitor to the work done by the battery in this process is |
|
Answer» `1 : 2 ` |
|
| 3659. |
(a) Define electrostatic potential at a point. Write its SI unit. Three charges q_(1), q_(2) and q_(3) are kept rspectively at points A, B and C as shown in figure Write the expression for electrostatic potential enery of the system. (b) Depict the equipotential surfaces due to (i) an electric dipole. (ii) two identical negative charges separated by a small distance. |
|
Answer» SOLUTION :(a) Electric potential at a point in an electric field is equal to the amount of work done by the EXTERNAL force (against the electric field) in order to bring a unit positive test charge (without acceleration) from infinity to that point. MATHEMATICALLY, electrostatic potential at a point A is given by `V_(A)=(W_(oo)rarrA)/(q_(0))`, where `W_(oo rarrA)` is the amount of work doen in order to carry a test charnge `q_(0)` from `oo` to the point A. Value of test charge should be as small as possible. SI unit of electric potential is volt (V). Potential is said to be 1 volt if a work of 1 J is being done to bring a positive charge of 1 C from infinity to that point. Expression for potential eneryg. U of hte combination of three charge is : `U=(1)/(4pi in_(0))[(q_(1)q_(2))/(r_(12))+(q_(1)q_(3))/(r_(13))+(q_(2)q_(3))/(r_(23))]` (b) (i) Equipotential surfaces due to an electric dipole are shown below : 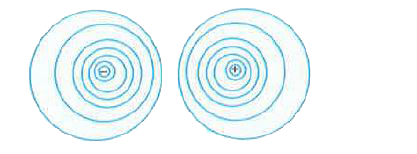 (ii) Equipotential surface due to two identical charges separated by a small distance .d. are shown below : 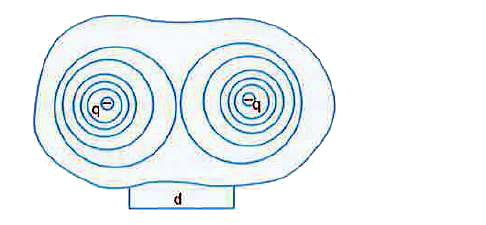
|
|
| 3660. |
An electric dipole has a fixed dipole moment vecp which makes angle 9 with respect to X-axis. When subjected to an electric field vecE_(1) = Ejhati ,it experience a torque vecT_(1) = tauveckWhen subjected to another electric field vecE_(2) = sqrt(3)E_(1)hatjit experiences a torque vecT_(2) - vecT_(1). The angle theta is: |
|
Answer» `60^(@)` 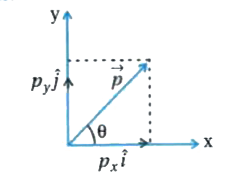 `vectau_(1) = VECP xx vecE` `=(p_(x)hati + p_(y)hatj) xx Ehati` `=-p_(y)Ehatk`………..(1) and `vectau_(2) =(p_(x)hati + p_(y)hatj) xx sqrt(3)Ehatj` `=sqrt(3)p_(x)Ehatk`………(2) but `vectau_(2) =-vectau_(1)` But `vectau_(2) =-vectau_(1)` `therefore sqrt(3)p_(x)Ehatk =-(-p_(y)Ehatk)` `therefore sqrt(3)=tan THETA` (From figure) `therefore theta = 60^(@)` |
|
| 3661. |
The intensity of central fringe in the interference pattern produced by two indetical slits is I. When one of the slits is closed then the intensity at the same points is I_(0). The relation between I and I_(0) is |
|
Answer» `I = 4I_(0)` |
|
| 3662. |
An a.c. is passed through a series LCR circuit What is the impedance of the circuit at resonance ? |
| Answer» Solution :At resonance IMPEDANCE of LCR series CIRCUIT is equal to the resistance (R) present in the circuit. | |
| 3663. |
An ideal gas undergoes a cyclic process as shown in the given P-T diagram, where ACis adiabatic. The process is also represented by: |
|
Answer»
|
|
| 3664. |
Sketch the variation of intensity of the interference pattern in Young's double-slit experiment. |
Answer» Solution :SEE figure. The central fringe is bright and on either side of it we GET alternate dark and bright fringes of UNIFORM fringe WIDTH. 
|
|
| 3665. |
Two radioactive nuclei A and B have their disintegration constant lambda_(A) and lambda_(B) respectively. Initially N_A and N_B number of nuclei are taken, then the time after which their undisintegrated nuclei are same is : |
|
Answer» `(lambda_(A) lambda_(B))/((lambda_(A)-lambda_(B))) ln (N_(B))/(N_(A))` `e^((lambda_(B)-lambda_(A))t)=(N_(B))/(N_(A))` `(lambda_(B)-lambda_(A))=ln ((N_(B))/N_(A))` `t=(1)/(lambda_(B)-lambda_(A)) ln ""N_(B)/(N_(A))` |
|
| 3666. |
A ray passing through focus of a convex mirror, after reflection passes through: |
|
Answer» POLE of mirror |
|
| 3667. |
The binding energy of a H-atom, considering an electron moving around a fixed nuclei (proton), is B=-(me^(4))/(8n^(2)epsilon_(0)^(2)h^(2)) (m=electron mass). If one decided to works in a frame of reference where the electron is rest, the proton would be moving around it. By similar arguments, the binding energy would be B=-(Me^(4))/(8n^(2)epsilon_(0)^(2)h^(2)) (M=proton mass) This last expression is not correct because |
|
Answer» n would not be integral |
|
| 3668. |
An explosion blows a rock into three pieces. Two pieces go off at right angles to each other. One of these two pieces of mass 1 kg moves with 12 m//s and other of mass 2 kg moves with 8 m/s. If the velocity of the third piece is 40 m//s, then its mass is: |
|
Answer» 5 kg `vecp_(2)=m_(2)upsilon_(2)=2xx8=16kgms^(-1)` SINCE total momentum is zero.:.`vecp_(3)`MUST be equal and OPPOSITE to resultant of `vecp_(1)`and`vecp_(2)` `:.m_(3)upsilon_(3)=sqrt(p_(1)^(2)+p_(2)^(2))=20impliesm_(3)=(20)/(40)=(1)/(2)kg` ` (##MOD_RPA_OBJ_PHY_C04_A_E01_008_S01.png" width="80%">Thus correct choice is (b). |
|
| 3669. |
Calculate the iterval (in eV units) between neighbouring levelsof free electrons in a metal at T=0 near the Fermi level, if the concentration of free electrons is n= 2.0.10^(22)cm^(-3) and the volume of the metal is V=1.0cm^(3). |
|
Answer» Solution :We WRITE expression for the NUMBER of electrons as `dN=(Vsqrt(2)m^(3//2))/(pi^(2)ħ^(3))E^(1//2)dE` Hence if `DeltaE` is the spacing between neighbouring levels near the FERMI level we must have `2=(Vsqrt(2)m^(3//2))/(pi^(2)ħ^(3))E_(F)^(1//2)DeltaE` (`2` on the `RHS` is to take care of both spins `f` electrons). Thus `DeltaE=(sqrt(2)pi^(2)ħ^(3))/(Vm^(3//2)E_(F)^(1//2))` But `E_(F)^(1//2)=(ħ)/(sqrt(2)m^(1//2))(3 pi^(2)n)^(1//3)` So `DeltaE=(2 pi^(2)ħ^(2))/(MV(3PI^(2)n)^(1//3))` Substituting the data we get `DeltaE= 1.79xx10^(-22)eV` |
|
| 3670. |
In a biprism experiment, the bandwidth is found to be increased bt 25^@ of initial. If D_1 = 64 cm then the distance between the slit and the eye-piece is : |
|
Answer» 80 mm |
|
| 3671. |
A nuclear reactor starts producing a radionuclide of half - life T at a constant rate R starting at time t = 0 The activity of the radionuclide at t = T is found to the A. Then (R )/(4) is |
|
Answer» `2:1` |
|
| 3672. |
On abruptly withdrawing the stretching force acting on a wire, its temperature will |
|
Answer» increase |
|
| 3673. |
Here is an example with this lesson plan: Generally you can choose any level to e the reference level, but once chosen, be consistent. A 2.0 kg sloth hangs 5.0 m above the ground (Fig. 8-23). (a) What is the gravitational potential energy U of the sloth-Earth system if we take the reference point y=0 to be (1) at the grund, (2) at a balcony floor that is 3.0 m above the ground, (3) at the limb, and (4) 1.0 m above the limb? Take the gravitational potential energy to be zero at y=0. |
|
Answer» SOLUTION :KEY IDEA Once we have chosen the reference POINT for `y=0`, we can calculate the gravitational potential energy U of the system relative to that reference point with Eq. 8-50. Calculations: For choice (1), the sloth is at `y=5.0` m, and `U - mgy = (2.0 kg) (9.8 m//s^(2))(5.0 m) =98 J`. For the other choices, the values of U are (2) `U = mgy = MG (2.0 m) = 39J`. (3) `U = mgy = mg(0) = 0J`, (4) `U = mgy = mg(-1.0m)= - 19.6 J ~~ - 20J`. |
|
| 3674. |
What are logic gates? Give the logic symbol of NOT and AND gates. |
|
Answer» SOLUTION :Logic gates : A logic gate is a digital circuit which PERFORMS a logical OPERATION logic SYMBOL of AND gate : 
|
|
| 3675. |
The volume of air space in the passenger compartment of an 1800 kg car is 5.00 m^(3) . The volume of the motor and front wheels is 0.710 m^(3), and the volume of the rear wheels, gas tank, and trunk is 0.800 m^(3), water cannot enter these two regions. The car rolls into a lake. (a) At first, no water enters the passenger compartment. How much of the car, in cubic meters, is below the water surface with the car floating (Fig. 14-45)? (b) As water slowly enters, the car sinks. How many cubic meters of water are in the car as it disappears below the water surface? (The car, with a heavy load in the trunk, remains horizontal.) |
| Answer» SOLUTION :(a) `1.80 m^(3),(B) 4.71 m^(3)` | |
| 3676. |
Here is an example with this lesson plan: Generally you can choose any level to e the reference level, but once chosen, be consistent. A 2.0 kg sloth hangs 5.0 m above the ground (Fig. 8-23). (b) The sloth drops to the ground . For each choice of refrence point, What is the change DeltaU in the potential energy of hte sloth-Earth system due to the fall? |
|
Answer» Solution :KEY IDEA The change in potential energy does not DEPEND on the choice of the refrence point for `y=0`, instead, it depends on the change in height `Delta y`. 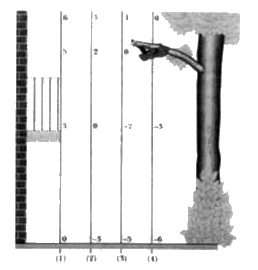 Figure 8-23Four choices of reference point `y=0`. Each y axis is marked in units of meters. The choice affects the value of the potential energy U of the sloth-Earth SYSTEM. However, it does not AFFECT the change `DeltaU` in potential energy of the system if the sloth moves by, say, falling. Calculation: For all four situations, we have the same `Delta y = -5.0m`. Thus, for (1) to (4) , Eq. 8-48 tells US that `Delta U = MG Deltay=(2.0kg)(9.8 m//s^(2))(-5.0m)` ` = -98` J. |
|
| 3677. |
Using the Bernoulli equation for a compressible flow derive the relation between the velocity of the flow at a given point and the local sound velocity. |
|
Answer» |
|
| 3679. |
Determine the .effective focal length. of the combination of the two lenses in Exercise 9.10, if they are placed 8.0 cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident ? Is the notion of effective focal length of this system useful at all . |
|
Answer» Solution :(i) Here `f_1 = 30 CM , f_2 = -20 cm , d= 8.0 cm` Where d = DISTANCE between two lenses. `rArr` If parallel rays incident on first lens in absence of second lens, `u_1 = oo ` and `f_1 = 30 cm` `therefore` From lens formula `1/f_1 = 1/v_1 - 1/u_1` `therefore 1/30=1/v_1 - 1/(-oo) = 1/(v_1) - 0` `therefore 1/30= 1/v_1` `therefore v_1 = 30 cm ` This image wil work as VIRTUAL object for second lens. `therefore u_e = (30 -8) = + 22 cm f_2 = - 20 cm ` From lens formula `1/f_2 = 1/v_2 - 1/u_2` `therefore 1/v_2 = 1/(-20) + (1)/(22) = (-22 + 20)/(440) = (-2)/(440)` `therefore v_2 = - (440)/(2) = - 220 cm` `rArr` Parallel rays coverged at 220-4 = 216 cm from mid-point of system two lenses. (ii) Let, parallel beam first incidents at left to concave mirror, `therefore u_1 = - oo ,f_1 = -20` cm From lens FORMUAL, `1 /f_1 = 1/v_1 - 1/u_1` `therefore1/v_1 = 1/f_1 + 1/u_1` `therefore 1/v_1 = (1)/(-20) + 1/(-oo) = - (1)/(20)+ 0` `therefore v_1 = -20 cm ` `rArr` This image wil work as real image for second lens, `therefore u_1 = - (20 + 8) = -28 cm ` `f_2 = 30 cm ` From lens formula `(1)/(f_2) = (1)/(u_2) - (1)/(u_2)` `therefore(1)/(v_2) = (1)/(f_2) + (1)/(u_2)` `therefore(1)/(v_2) = (1)/(3) + (1)/(-28) = (14 -15)/(420) = - (1)/(420)` `thereforev_2 = - 420 cm ` The parallel beam appears to diverge from a point 420 - 4 = 416 cm on the left of the centre of the two lens system. From the above tow cases it concludes that the answer DEPENDS on which side of the lens system the parallel beam in incident. So, the notion of effective focal lenght doesn.t seem to ve useful here. |
|
| 3680. |
what is the time period of revolution of a geostationary Satellite of earth? |
|
Answer» a)T |
|
| 3681. |
A plane electromagnetic wave of frequency 25 MHz travels in free space along the x - direction.At a particular point in space and time, E=6.3 hat(j) V/m. What is B at this point ? |
|
Answer» Solution :The magnitude of B is `B=(E )/(c )=(6.3V//m)/(3XX10^(8)m//s)=2.1xx10^(-8)T` To find the direction, we note that E is along y-direction and the wave propagates along x-axis. Therefore, B should be in a direction perpendicular to both x and y-axes. Using vector algebra, `E XX B` should be along x - direction. Since,`(+hat(J))xx (+hat(K))=hat(i)`,B is along the z-direction.Thus `B=2.1xx10^(-8)hat(k)T`. |
|
| 3682. |
A spherical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that the whole of it is just immersed in water is : |
|
Answer» <P>`5/12pir^(4)PG` `=Vprg-V/2p[3/8r].` Now `V=4/3pir^(3)` `THEREFORE` Gain in P.E. `=4/3pir^(4)pg-1/4pir^(4)pg=13/12pir^(4)pg` Loss of P.E. of ball =`4/3pir^(4)`p. g or work DONE `=13/12pir^(4)pg-4/3pir^(4)p.g` `therefore` Work done=`pir^(4)pg[13/12-4/3(p.)/p]` `=pir^(4)pg[13/12-4/3xx0.5]` `5/12pir^(4)p.g` CORRECT choice is (a). |
|
| 3683. |
Bohr's basic idea of discrete energy levels in atoms and the process of emission of photons from the higher levels to lower levels was experimentally confirmed by experiments performed by |
|
Answer» MICHELSON- MORLEY |
|
| 3684. |
A double convex thin lens made of glass of refractive index 1.6 has radii of curvature 15 cm each. The focal length of this lens when immersed in a liquid of refractive index 1.63 is : |
|
Answer» -407 cm |
|
| 3685. |
There are 21 marks (zero to 20) on the dial of a galvanometer, that is there are 20 divisions. On passing 10muA current through it, it shows a deflection of 1 division. Its resistance is 20Omega. (a) How can it be converted into an ammeter which can measure 1 A current ? (b) How can we change it into a voltmeter to measure a pd of 1 V ? Also find the effective resistance of both of the above mentioned meters. |
|
Answer» Solution :1. When a current of `10MUA` passes through the galvanometer, its pointer shows a deflection of 1 division. There are 20 divisions in this galvanometer. `therefore` The maximum current which can be measured by it (current capacity) `I_(G)=10xx10^(-6)xx20=200xx10^(-6)A`. 2. For ammeter, the REQUIRED shunt to be joined in parallel to galvanometer is, `S=(GI_(G))/(I-I_(G))` = `(20xx200xx10^(-6))/(10000xx10^(-4)xx10^(-4))` = `(20xx2xx10^(-4))/(10000xx10^(-4)xx10^(-4))` = `40/9998~~0.004Omega` `I_(G)=200xx10^(-6)A` = `2xx10^(-4)A` `G=20Omega` I = 1 A = `10000xx10^(-4)A` 3. THUS to convert this galvanometer into an ammeter which can measure 1A current, a shunt of `0.004Omega` should be joined. The effective resistance of this ammeter will be `G.=(GS)/(G+S)=(20xx0.004)/(20+0.004)~~0.004Omega`. 4. In order to convert the galvanometer into a voltmeter, the required series resistance is `R_(S)=V/I_(G)-G` = `1/(2xx10^(-4))-20` = `0.5xx10^(4)-20` = 5000 - 20 = `4980Omega` Here, V = 1 volt `I_(G)=2xx10^(-4)A` `G=20Omega` 5. In order to convert this galvanometer into a voltmeter which can measure 1 volt, a series resistance of 4920 should be joined with it. The effective resistance of this voltmeter will be `R._(S)=R_(S)+G=4980+20=5000Omega`. (`thereforeR_(S)` and G are in series) |
|
| 3686. |
The IV characteristic of an LED is: |
|
Answer»
|
|
| 3687. |
In previous question, if the total distance covered by the car is s, the maximum speed attained by it will be : |
|
Answer» `(2S.(a_1a_2)/(a_1+a_2))^((1)/(2) ) ` ` ""S= (VM^(2))/(2) ((1)/(a_1)+(1)/(a_2)) ,"" V_m =(2s (a_1a_2)/(a_1+a_2)) ^(1//2)` |
|
| 3688. |
A resistance of R draw current from a potentiometer. The potentiometer wire, AB, has total resistance of R_(0). A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of potentiometer wire. |
Answer» Solution :Derivation of expression of voltage ACROSS resistance R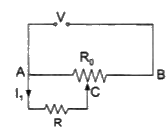 Resistance between points A & C `1/(R_1))=(1/R+1/((R_(0))/2))` Effective resistance between points A & B. `R_(2)=((R(R_(0))/2)/(R+(R_(0))/2))+(R_(0))/2` Current drawn from the voltage source. `1=V/((R(R_(0))/(R+(R_(0))/2)+(R_(0))/2)` LET current through R be `I_(1)` `I=(I((R_(0))/2))/(R+(R_(0))/2)` Voltage across R `V_(1)=I_(1)R` `=(IR_(0))/(2(R+(R_(0))/2)).R=("RR"_(0))/(2(R+(R_(0))/2)) . V/(("RR"_(0))/(2R+R_(0)))+(R_(0))/2` `=(2RV)/(R_(0)+4R)` |
|
| 3689. |
Draw logic diagrams for the Boolean expressions given below. (i)A . barB+barA . B=Y , (ii)(A+barB). (barA+B)=Y |
Answer» Solution :(i) The REQUIRED logic diagram for the given Boolean expression is given in FIGURE. Here the input B before applying to first AND GATE and input A before applying to second AND gate have been inverted. The output these gates are, THEREFORE, `AbarB` and `barAB` respectively. These outputs are FED to OR gate which gives `Y = AbarB+ barAB` as shown in figure.  (ii) The required logic diagram for the given Boolean expression is shown in figure. The input B to first OR gate and input A to second OR gate have been inverted, The output of these gates are, therefore, `A+barB` and `barA+B` as shown. These inputs when applied to AND gate give the required output. `Y=(A+barB).(barA + B)` 
|
|
| 3690. |
A slab of material of dielectric constant K has the same area as the plates of a parallel-plate capacitor but has a thickness (3/4)d. where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates? |
|
Answer» Solution :Let `E_(0)=V_(0)/d` be the electric field between the PLATES when there is no dielectric and the potential difference is `V_(0)`. If the dielectric is now inserted, the electric field in the dielectric will be `E=E_(0)/K`. The potential will then be `V=E_(0) (1/4 d)+E_(0)/K (3/4 d)=E_(0) d(1/4+3/(4K))=V_(0) (K+3)/(4K)` The potential difference decreases by the factor `((K+3))/(K)` while the free charge `Q_(a)` on the plates remains unchanged. The capacitance thus INCREASES. `C=Q_(0)/V=(4K)/(K+3) (Q_(0))/(V_(0))=(4K)/(K+3) C_(0)` |
|
| 3691. |
Define capacitance of a capacitor. |
| Answer» Solution :CAPACITANCE of a capacitor is DEFINED as the ratio of CHARGE Q on a plate of pacitor to the potential DIFFERENCE V across its plates i.e., `C = Q/V`. | |
| 3692. |
The unit of a physical quantity which does not depend on the unitofany other physical quantity is called |
|
Answer» INDEPENDENT dimension |
|
| 3693. |
An insect trapped in a circular groove of radius 12 cm moves along the groove steadily and completes7 revolutions in 100 s. (a) What is the angular speed, and the linear speed of the motion ?(b)Is the acceleration vector a constant vector ? What is Us magnitude ? |
|
Answer» Solution :This is an example of uniform circular motion. Here, R =12 cm. The angular speed `omega` is GIVEN by `omega = 2pi//T =2pi xx 7//100 = 0.44` rad/s The LINEAR speed V is: `v=omegaR =0.44S^(-1) xx 12 cm = 5.3 cm S^(-1)` The direction of velocity v is along the tangent to the circle at every point. The acceleration is directed towards the centre of the circle. Since this direction changes continuously, acceleration here is not a constant vector. However, the magnitude of acceleration is constant : `a = omega^(2)R =(0.44 S^(-1))^(2) (12 cm) = 2.3 CMS^(-2)` |
|
| 3694. |
The working of which of the following is similar to that of a slide projector? |
|
Answer» Electron MICROSCOPE |
|
| 3695. |
Which group of people did not join the Jacobin club? |
|
Answer» Artisans |
|
| 3696. |
A secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380 Omega. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car? |
| Answer» SOLUTION :`0.005 A`, impossible because a STARTER motor REQUIRES LARGE current (`~ 100 A)` for a few seconds | |
| 3697. |
A rectangular coil of N-turns, area A is held in a uniform magnetic field B. If the coil is rotated at a steady angular velocity omega, deduce an expression for the induced emf in the coil at any instant of time. |
|
Answer» SOLUTION :Consider a rectangular coil PQRS of N turns, each of area A, held in a uniform magnetic field `VECB`. Let the coil be rotated at a steady angular VELOCITY w about its own axis. Let at any instant t, normal to the area (i.e., the area vector `vecA`) subtends an angle `THETA = omega t` from direction of magnetic field `vecB`. Then, at that moment, the magnetic flux linked with the coil is ` phi_(B) = NvecB.vecA = NB Acos theta = NB Acos omegat` `THEREFORE` Induced emf `varepsilon = - (dphi_(B))dt = - d/dt (N B A cos omegat)` ` =-N B A d/dt(cos omegat) = N B A omegat` where `varepsilon_(0) = N B A omega` = maximum value of induced emf. If the coil be rotating at .f. revolutions per second, then `omega = 2pif` and the maximum induced emf `varepsilon_(0) = NBAomega = 2pifNBA` 
|
|
| 3698. |
An electric refrigerator abstracts 2000 calories from ice trays. The coefficient of performance is 5. Then the work done by motor in calories, is : |
|
Answer» 5 |
|
| 3699. |
In an experiment, electrons are made to pass through a narrow slit of width d comparable to their de-Brogile wavelength. They are detected on a screen at a distance D from the slit. Which of the following graphs can be expected to represent the number of electrons N detected as a function of the detector position y(y = 0 corresponds to the middle of the slit)? |
|
Answer»
|
|
| 3700. |
A mica slab of thickness equal to the distance between the two plates of a parallel plate air capacitor is inserted in the space between the plates. Explain the changes in capacitance in the following case, When the mica slab is inserted partially. |
Answer» Solution :Fig.4.47 shows the partial INSERTION of the mica slab in the SPACE between the plates of the PARALLEL plate air capacitor. Let the area of the plates of the capacitor be `alpha`, the area of the mica slab inside the capacitor be `alpha_1(alpha_1 lt alpha)`, distance between the plates of the capacitor be d and the DIELECTRIC constant of mica be k.  Therefore, TOTAL capacitance of the capacitor, C = capacitance of parallel plate capacitor of area `alpha_1` with mica as dielectric + capacitance of parallel plate air capacitor of area `(alpha- alpha_1)` `= (in_0 k alpha_1)/(d)+(in_0(alpha-alpha_1))/(d)= (in_0 alpha)/(d)+(in_0 alpha_1(k-1))/(d)` So due to partial insertion of the mica slab, the capacitance increases by `(in_0alpha_1(k-1))/(d)`. |
|