Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 44951. |
An amplitude modulated wave is as shown in Fig. Which of the following is/are correct ? |
|
Answer» The percentage of modulation is 66.67% |
|
| 44952. |
Three point charges + q each are kept at the vertices of an equilateraltriangleof side l. Determinethe magnitude and sign of charge to be kept at the centroid so that charges at the vertices remain in equillibrium. |
|
Answer» `Q = (2q)/(sqrt(3))`  `vec(F_(1))` = force at A due to charge at B `= (1)/(4pi in_(0)) (q^(2))/(L^(2))`, along `vec(BA)` `vec(F_(2))` = forceat A due to charge at C `= ((1)/(4pi in_(0)) (q^(2))/(l^(2)))`, along `vec(CA)`. `vec(F_(1)) + vec(F_(2)) = sqrt(F_(1)^(2) + F_(2)^(2) + 2F_(2)F_(2) cos60^(0))` `= F_(1) sqrt(3) = (sqrt(3)q^(2))/(4pi in_(0) l^(2))` along GA. Force at A due to chargeQ at the CENTROID G `= (1)/(4pi in_(0)) (Qq)/(AG^(2)) = (Qq)/(4pi in_(0) (l// sqrt(3))^(2)) = (3Qq)/(4pi in_(0) l^(2))` This mustbe EQUALAND opposite to `(vec(F_(1)) + vec(F_(2)))` `:. (3Qq)/(4pi in_(0) l^(2)) =(- sqrt(3) q^(2))/(4pi in_(0) l^(2))` `Q = (q)/(sqrt(3))` |
|
| 44953. |
Resistivity of ideal conductor and idealinsulator are rho_(1) and rho_(2) respectively, then ..... |
|
Answer» `rho_(1) = 0, rho_(2) =0` |
|
| 44954. |
A rectangular coil of dimensions 40 cm xx25 cm having 1000 turns rotates in a uniform magnetic field of strength 0.08 Wbm^(-2) about an axis perpendicular to the field. If the coil makes 300 revolution per minute, find the instantaneous emf when the plane of the coil make and angle of (i) 0^(@) (ii) 45^(@) and (iii) 90^(@) with the magnetic lines of force. |
|
Answer» |
|
| 44955. |
A long current carrying wire, carrying current I_(1) such that I_(1) is flowing out from the plants of paper is placed at O. A steady state current I_(2) is flowing in the loop ABCD. |
|
Answer» The net force is zero 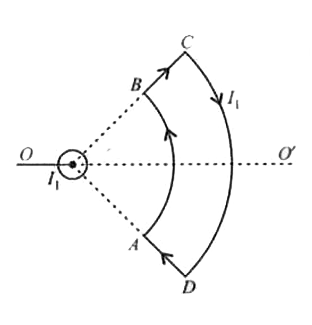 (a) The forces on BC and CD are equal and opposite. `:.` The net force on ABCD is zero. Torque on loop ABCD: The equal and opposite forces, on BC and AD, constitute a torque which, as seen from O, will rotate the loop in clockwise direction, along OO. as axis. |
|
| 44956. |
A 100 turn closely wound circular coil of radius 10 cm carries a current of 3.2 A. a. What is the field at the centre of the coil ? b. What is the magnetic moment of this coil ? The coil is placed in a vertical plane and is free to rotate about a horizontal axis which coincides with its diameter. A unifrom magnetic field of 2 T in the horizontal direction exists such that initially the axis of the coil is in the direction of the field. The coil rotates through an angle of 90^@ under the influence of the magnetic field . c. What are the magnitudes of the torques on the coil in the initial and final position ? d. What is the angular speed acqired by the coil when it has rotated by 90^(@) ? The moment of inertia of the coil is 0.1 kg m^2 |
|
Answer» Solution :`B = (mu_0 NI)/(2R)` Here, N =100, I = 3.2 A, and R = 0.1 m . Hence, `B = (4 PI xx 10^(-7) xx 10^(2) xx 3.2 )/(2 xx 10^(-1))``= (4 xx 10^(-5) xx 10)/(2 xx 10 ^(-1)) (" using " pi xx 3.2 = 10)` The direction is given by the right - hand thumb rule. b. The magnetic moment is given by `m = NI A = NI pi r^2 = 100 xx 3.2 xx 3.14 xx 10^(-2) = 10 Am^2` The direction is given by the right hand thumb rule . c. `tau = | m xx B| = mB sin theta` Initially, `theta = theta` Thus, inital torque `tau_i =0` Finally , `theta = (pi)/(2) ( or 90^@)` Thus , FINAL torque ` tau_t = mB =10 xx 2 = 20 Nm ` d. Prom Newton.s second law, `I (d omega)/(dt) = m B sin theta` where I is the moment of inertia of the coil. From chain rule, `(domega)/(dt)=(domega)/(d theta)(d theta)/(dt)=(d omega)/(d theta) omega` Using this , `I omega d omega = m B sin theta d theta ` Intergrating from `theta = 0 " to " theta = pi/2 ,1 int_(0)^(OMEGAR) omegadomega = mBint_(0)^(pi//2)sin theta d theta` `I (omega_r^2)/(2) =- mB COS theta "|"_(0)^(pi //2) = m B` `omega_(f) = ((2mB)/(I))^(1/2) = ((2 xx20)/(10^(-1))) ^(1/2) = 20 s^(-1)` |
|
| 44957. |
What is power factor ? |
|
Answer» SOLUTION :POWER factor is defined as the ratio betwqeen true power to apparent power. It is given by `cosphi`= True power/apparent power where F is phase DIFFERENCE between E nd I. |
|
| 44958. |
Explain arrangement of Davission and Germer experiment. |
|
Answer» Solution :The WAVE nature of electron was first experimentally verified by C.J. Davission and L.H. Germer in 1927 and G.P.Thomson in 1928. Davisson and Thomson shared Nobel Prize in 1937 for their experimental discovery of diffraction of electron by crystals. Experimental arrangement:Figure shows schematic arrangement of Davisson and Germer experiment.  It consist of an electron gun which comprises of tungsten filament F,COATED with barium oxide and heated by a low voltage power supply (L.T. battery)filament is heated by passing current through L.T. Battery. It consist of an electron gun which comprises of tungsten filament F,COATED with barium oxide and heated by a low voltage power supply (L.T. battery)filament is heated by passing current through L.T. Battery. When filament is heated due to thermionic emission electrons are EMITTED which are accelerated by H.T. battery to a desired velocity. Thses electrons are made to pass through a cylinder with fine HOLES along axis producing a fine collimated beam.The beam is made to fall on the surface of the crystal. Electrons are scattered in all directions by atoms of crystal . THe intensity of electron beam scattered in given DIRECTION is measured by electron detector (collector). The detector can be moved on a circular scale and it is connected with sensitive galvanometer which records currents. The deflection of the galvanometer is proportionl to the intensity of the electron beam entering the collector. The apparatus is enclosed in an evacuated chamber. |
|
| 44959. |
A parallel wire line has air as dielectric. What can be the minimum characteristic Impedance of such a line? |
|
Answer» |
|
| 44960. |
How we correct astigmatism by using what? |
| Answer» SOLUTION :CYLINDRICAL LENS | |
| 44961. |
Obtain the equation of electric field by dipole at a point on axis of dipole. |
Answer» Solution :Let the point P be at distance R from the centre of the dipole on the SIDE of the charge q as shown in figure, then electric field by - q charge.  The electric field by `-q` charge `vecE_(-q) =-q/(4pi epsilon_(0)(r+a)^(2))hatp =(-kq)/(r+a)^(2)hatp` (`therefore` distance from `-q` to `P = r+a`).........(1) Electric field by `+q` charge. `vecE_(+q) = -q/(4pi epsilon_(0)(r-a)^(2))hatp = - (kq)/(r-a)^(2) hatp` (`therefore` distance from `+q` to P `=r -a)`.......(2) The unit field at P is `vecE =vecE_(+q) + vecE_(-q) = kq[1/(r-a)^(2) -1/(r+a)^(2)] hatp_(n)` (`therefore` From equation (1) and (2) ) `therefore vecE = kq(4ar)/(r^(2)-a^(2))^(2)hatp`..........(3) For `r gt gt a, r^(2) -a^(2) = r^(2)`, using in equation (3) `vecE= (k(4qa))/(r^(3))hatp =(2kp)/r^(3) (therefore p = q(2A))`..........(4) |
|
| 44962. |
When an oscillator completes 100 oscillations its amplitude reduced to 1/3 of initial value. What will be its amplitude, when it completes 200 oscillations? |
|
Answer» `1//8` Now, when `t= 100 T, a=a_(0)//3`[T is time period] Let the amplitude be a at t= 200 T i.E, after completing 200 oscillations. `therefore a =a_(0)//3 = a_(0)e^(-100Th)`............ (i) and `a. = a_(0)e^(-200 Th)`........(ii) From (i) `1/3 = e^(-100Th), therefore e^(-200 Tb) = 1//9` From (ii), `a. = a_(0) xx 1/9 =a_(0)/9` `therefore` The amplitude will be reduced to 1/9 of initial value. |
|
| 44963. |
A : Light waves travel through vacuum where as sound waves can.t R : Light waves are mechanical waves whereas sound waves are electro-magnetic |
|
Answer» Both A and R are true and R is the correct EXPLANATION of A |
|
| 44964. |
A magnetic field of 100 G (1 G = 10^(-4) T) is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10^(-3) m^2 . The maximum current-carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a core is at most 1000 turns m^(-1). Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is notferromagnetic. |
| Answer» Solution :LENGTH about 50 cm, radius about 4 cm, number of turns about 400, current about 10 A. These particulars are not unique. Some ADJUSTMENT with limits is possible. | |
| 44965. |
Two resistors when connected in series net resistance is 5 Omega and when they are connected in parallel net resistance is 1.2 Omega What are these resistors? |
|
Answer» `2 OMEGA,3 Omega` |
|
| 44966. |
A moving coil galvanometer of resistance 50Omega is connected in series with a fixed resistance 50Omega and the combination toa cell of steady emf and negligible internal resistance. What is the shunt required to halve the current through the galvanometer? |
|
Answer» |
|
| 44967. |
If a particle takes 0.5 sec to reach position of minimum velocity from previous such position, then |
|
Answer» T = 6 SEC, V = 1/6 HZ |
|
| 44968. |
The dimension formula of the magnetic field intensity B is ______ . |
|
Answer» `ML^(-2)A^(-1)` `therefore` The dimension formula of, `B=("(Dimenstion formula of F)")/("(Dimension formula of I)(Dimenstion formula of l)")` `=(M^(1)L^(1)T^(-2))/(A^(1)L^(1))` = `MT^(-2)A^(-1)` |
|
| 44969. |
A thin biconvex lens of refractive index 3//2and radius of curvature 50cm is placed on a reflecting convex surface of radius of curvature 100cm. A point object is placed on the principal axis of the system such that its final image coincides with itself. Now, few drops of a transparent liquid is placed between the mirror and lens such that final image of the object is at infinity. Find refractive index of the liquid used. Also, find the position of the object. |
|
Answer» POWER of LENS, `P_(L)=(1)/(f_(l))=((3)/(2)-1)((1)/(50)-(1)/(-50))=(1)/(50)` `:.` Power of equivalent mirror `P_(EM) =2P_(l)+P_(m)=(2)/(50)-(1)/(50)=(1)/(50)` i.e., Focal length of equivalent mirror `f_(CM)=-50` Since image and object coincides, hence position of the object is at the center of curvature of the equivalent mirror,i.e., at `2f_(cm)=100cm` from the lens. When the liquid of refractive index be isplaced between the lens and convex mirror, it forms a liquid lens of power, `p_(u)=((1)/(-50)-(1)/(100))=(3(l-mu))/(100)` Now, power of equivalent mirror `=2P_(l)+2P_(u)+P_(m)` `=(2)/(50)+(2xx3(1-mu))/(100)+(1)/(-50)=(3(1+mu)+1)/(50)` (i) Since final image is at infifnity, hence the object should be at its focal point i.e., `f_(EM)^(')=100` `rArr =-(1)/(f_(EM)^('))=(1)/(100)` (ii) From Eqs (i) and (ii), we get `(3(1-mu)+1)/(50)=(1)/(100)` `rArr mu=7//6` |
|
| 44970. |
Photons of equal energy were incident on two different H-like samples, one containing He ions in n_(1) state and other containing Li^(++) ions in n_(2) state. The incident photons ionises both the samples. If the difference in KE^(8) of the ejected electrons in is 2.55 eV then magnitude of difference in the states of the two ions may be : |
|
Answer» 8 |
|
| 44971. |
Explain first focal centre and second focal centre for lens. |
Answer» SOLUTION :(i) First FOCAL point : Position of object from which IMAGE formed by lens at INFINITY is called first focal point `(F_1)`. Second focal point : Position of point like image formed by lens for object at infinity is called second focal point `(F_2)`. 
|
|
| 44972. |
Two small spheres of radius 'a' each carrying charges +q and -q are placed at points A and B, distance d apart. Calcualte potential difference between points A and B. |
|
Answer» `= (1)/(4PI in_(0)) XX (Q)/(d) - (1)/(4pi in_(0)) ((-q))/(d) = (2q)/(4pi in_(0) d)` |
|
| 44973. |
Name c.g.s and S.I. units of charges. |
|
Answer» SOLUTION :The c.g.s units of charge is 1 STAT COULOMB or 1 e.s.u. of charge. SI UNIT of charge is 1 coulomb 1 Coulomb = `3xx10^9` stat coulomb |
|
| 44974. |
If wavelengths of light in liquid A and B are 3500 Å and 7000 Å respectively, then critical angle of liquid A with respect to liquid B is ..... |
|
Answer» `15^@` but`1/n=(v_A)/(v_B)=(lambda_Af)/(lambda_Bf)`[`because` F is constant] `therefore1/n=(lambda_A)/(lambda_B)=(3500)/(7000)` `1/n=1/2` sinC=`1/2` `therefore C=sin^(-1)(1/2)` `thereforeC=30^@` |
|
| 44975. |
What is the ratio of radii of the orbits corresponding to first excited state and ground state in a hydrogen atom? |
|
Answer» Solution :We knowthat radius of nith orbit in a hydrogen atom is GIVEN by `r_(N) = r_(0)n^(2)`, where `r_(0)` = radiusof orbitin stablein stablestatecorrespondington = 1 . `THEREFORE `radiusof hydrogenorbitin firstexcitedstate`(n = 2) r_(2) = r_(0) (2)^(2) = 4r_(0)` `rArr "" (r_(2))/(r_(1)) =(r_(2))/(r_(0))= (4)/(1)` |
|
| 44976. |
The variation of the intensity of magnetisation with respect to the magnetisign field Hin a diamagnetic substance is described by the graph |
| Answer» Answer :B | |
| 44977. |
A missile is launched at an angle of 60^(@) to the vertical with a velocity sqrt( 0.75gR) from the surface of the earth ( R is the radius of the earth). Find the maximum height from the surface of earth. (Neglect air resistance and rotating of earth). |
|
Answer» |
|
| 44978. |
Conservatios of charge is the propery by virtue of whichtotal charge of an isolatedsystem always remainsconstant or conserved. For example, whenwe rub two inslatingbodies, A and B, suchthat n electrons fromA transfer to B, then chargeacquiredby A = + ne and chargeacquired byB = -ne, where e is magnitudeof chargeon electron. The net chargeon isolated systemof bodiesA and B =n e -ne - 0, which was the chargebefore rubbing. Thus, itis not possibleto create or destroynet charge carriedby any isolated system. It also imples that chargescan be created or destroyedin equaland unlike pairs only. (i) What is the basic causeof conservationof charge ?(ii) Name any other fundamentalpropertyof electric charge. (iii) At a time, can you createtwo likecharges of magnitudeq =n e each ? (iv) How is the property of conservation of charge reflected in day to day life ? |
|
Answer» SOLUTION :(i) As is known, CHARGING is dueto actualtransfer of electrons from one day to the other. Assuming that there is no stay lossloss of electrons number of electrons gainedby one body is equalto number of electrons lost by the other body. This is the basiccause of CONSERVATION of charge. (ii) Another fundamentalof electric charge is'Quantization of charge'. (iii) No, as it is against the conservation of charge. Creationof a charge `+q` is ACCOMPAINED by creations of charge `-q`. (iv)In day to daylife, conservation of charge impliesthat gainof oneis alwaysequal to lossof the other. It also imples that sumtotal of gain in lifeis equalto sumtotal of losses in LIFE infact, the sum total of gainsand losses in lifeis constant. |
|
| 44979. |
A two wire transmission line has a capacitance of 20 pF/m and a characteristic impedance of 50 Omega (a) What is the inductance per metre of this cable ? (b) Determine the impedance of an infinitely long section of such cable. |
|
Answer» Solution :(a) The CHARACTERISTIC impendance `Z=sqrt(L//C)L=(Z^(2))(C)=(50)^(2)(20xx10^(-12))H=0.05H`. (b) The characteristic impedance of a trasnmission line is the impedance that an infinite length of line would PRESENT to a power supply at the input end of the line. Thus, `Z_(oo)=Z_(0)=50Omega`. |
|
| 44980. |
A beam of light is incident normally upon a polaroid and the intensity of the emergent beam is found to be unchanged when the polaroid is rotated about an axiis perpendicular to its pass axis. The incident beam is ____in nature. |
|
Answer» |
|
| 44981. |
Obtain an expression for the equivalent emf and internal resistance of two cells connected in parallel. |
Answer» Solution :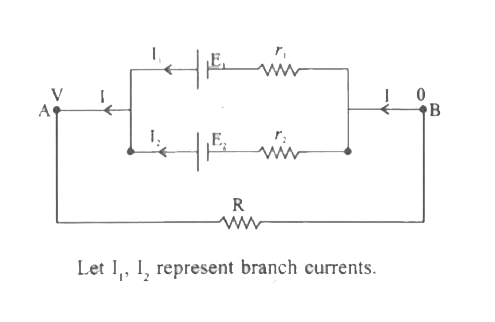 LET `I_1,I_2` represent branch currents. Let V be the commonpotential ,so that , `I_1=(E_A-V)/r_1, I_2=(E_2-V)/r_2` hence, `I=(E_1-V)/r_1 + (E_2-V)/r_2` i.e., `I=(E_1/r_1 + E_2/r_2)-V (1/r_1+1/r_2)` Comparingthis with the terminalpotentialdifference, `V_E_(eq)-Ir_(eq)` i.e.,`V=E_(eq)-1/((1/r_(eq)))` For two CELLS in parallel COMBINATION , `(E_(eq))_p=(E_1/r_1 +E_2/r_2)/(1/r_1+1/r_2)=(E_1r_2 + E_2r_1)/(r_1+r_2)` `1/(r_(eq))_p =1/r_1+1/r_2`and main current=`i=E_(eq)/(R+r_(eq))` Note : (i) For .n. cells in parallel `V=[(sum_(r=1)^n E_i/r_i)/(sum_(i=1)^n 1/r_1)]-[I/(sum_(i=1)^n 1/r_1)]` , `(E_(eq))_"parallel" =[(sum_(r=1)^n E_i/r_i)/(sum_(i=1)^n 1/r_1)]-[I/(sum_(i=1)^n 1/r_1)]` and `(1/r_(eq))_(p)=sum_(i-1)^n (1/r_i)`. (ii) For .n. number of identicalcells E-emf of each CELL r-internalresistance of each cell. `(E_(eq))_p =(n(E/r))/(n(1/r))` i.e.,`(E_(eq))_p=E` and `(1/r_(eq))_p=n(1/r)` i.e. `(r_(eq))_p =r/n` Main current, `I=(nE)/(R+n/r)` and terminalpotential difference across cells V=IR. |
|
| 44982. |
How much work has to be done to isolate the two charges and take them infinitely away from each other? |
|
Answer» |
|
| 44983. |
Ruby lases at a wavelength of 694 nm. A certain ruby crystal has 4.00xx10^(19)Cr ions (which are the atoms that lase). The lasing transition is between the first excited state and the ground state, and the output is a light pulse lasting 1.50mus. As the pulse begins, 60.0% of the Cr ions are in the first excited state and the rest are in the ground state. What is the average power emitted during the pulse? |
| Answer» SOLUTION :`1.5xx10^(6)J//s=1.5xx10^(6)W` | |
| 44984. |
A body of mass 5 kg collides elastically with a stationary body of mass 2.5 kg. After the collision, the 2.5 kg body begins to move with a kinetic energy of 8). Assuming the collision to be one-dimensional, the kinetic energy of the 5 kg body before collision is: |
|
Answer» 3 J =`(4X)/((1+x)^2)=(4xx1/2)/((1+1//2)^2)` =8/9 This means that `("K.E of 2.5 KG after collison")/("K.E of 2.5 Kg before collison")=8//9` `:.` K.E of 5 kg before collison is `E_k=9//8xx8=9 J` |
|
| 44985. |
A particle of mass m is attached to one end of missless rigid non-conducting rod of length l. Another particle of the same mass is attached to the other end of the rod. Two particles carry charges +q and -q . Thisarrangement is held in the region of uniform electric field E such that the rod makes and angle theta (lt 5^(@)) withthe fielddirection. Find an expression for the minimum time that is needed for the rod to become parallel to the field after it is set free. |
|
Answer» Solution :As the rod has twocharges of EQUAL MAGNITUDE(be opposite in nature), the torqueacting on the rod, `tau=qE xx l sin theta` or, `tau =qE l theta""[ becausetheta LT 5^(@)]` We know, `tau=I alpha` [where I = moment ofinertia and `alpha` = angular acceleration] 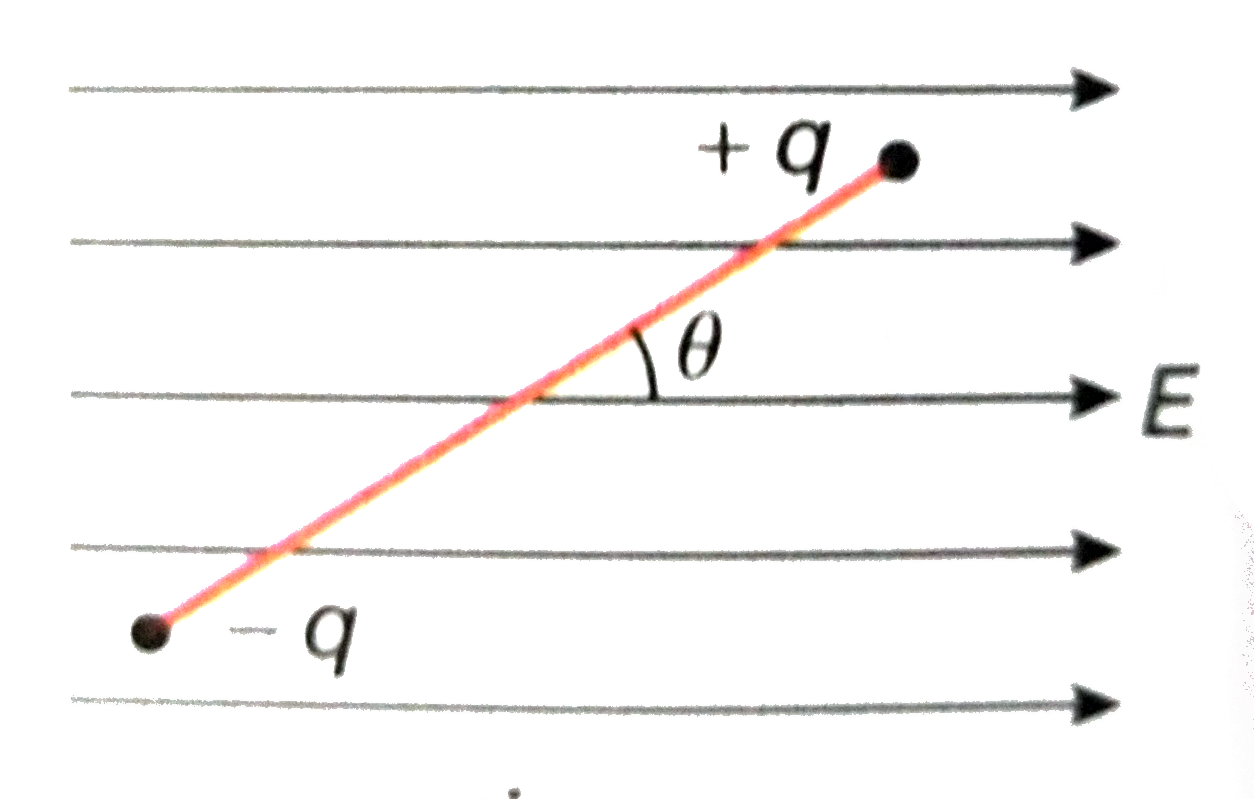 Hence, `I alpha=q E l theta or, alpha=(q E l theta)/(I)` `therefore` TIME period, `T=2pi sqrt(("angular displacement")/("angular acceleration"))=2pi sqrt((I)/(qE l))` Now, moment ofinertiaof the DIPOLE, `I=[((l)/(2))^(2)+((l)/(2))^(2)]m=(1)/(2) ml^(2)` `therefore T=2pisqrt((ml^(2))/(2qEl))=2pi sqrt((ml)/(2qE))` `therefore ` Required time, `t=(1)/(4)xx "time period"=(T)/(4)=(pi)/(2) sqrt((ml)/(2qE))` |
|
| 44986. |
A uniform solid sphere has a radius R and density p. The M.I. of sphere passing through its centre is |
|
Answer» 28/15`PI R^5rho` |
|
| 44987. |
An laternativing voltage of 350 V, 60 Hz is applied on a full wave rectifier. The internal resistance of each diode is 200Omega. If R_(L)=5kOmega, then find (i) the peak value of output current. (ii) the value of output direct current. (iii) theoutput dc power. (iv) the rms value of output current. (v) the efficiency of rectifier. (vi) the value of peak inverse voltage (P.I.V.). |
|
Answer» <P> Solution :(i) `I_("PEAK")=I_("rms")xxsqrt2=(V_("rms")xxsqrt2)/((R_(L)+2r_(p)))``or I_(0)=(350xxsqrt5)/(5400)=0.092A` (II) `I_(DC)=(2I_(0))/(pi)=(2xx0.092)/(3.14)=0.058A` (iii) `p_(DC)=I_(DC)^(2)xxR_(L)=(0.058)^(2)xx(5000)=17W` (iv) `I_("rms")=(I_(0))/(sqrt2)=(0.092)/(1.41)=0.065A` (v) Efficiency of reaction `eta=(81.6)/(1+(r_(p))/(R_(L)))` `or eta=(81.6)/(1+(200)/(5000))=(81.6xx25)/(26) or eta=78%` (VI) `P.I.V.=2E_(0)` `or P.I.V.=2sqrt2E_("rms")=2sqrt2=350` `or P.I.V.=1000V`. |
|
| 44988. |
The cube in figure has edge length sqrt2m and is oriented as shown in a region of uniform electric field , in newtons per coulomb, is given by (a)6.00hati, (b) -2.00 hatj, and (c) -3.00 hatj+ 4.00 hatk . (d) what is the total flux through the cubefor each field ? |
|
Answer» |
|
| 44989. |
Optical fibers work on the principle of ___________. |
| Answer» SOLUTION :TOTAL intermal REFLECTION | |
| 44990. |
Find the capacitance of the capacitor that would have a reactance of 100 Omega when used with an a.c. source of frequency 5/pi kHz. |
|
Answer» Solution :Here, `X_(C) = 100 Omega, v= 5/pi kHz = 5000/pi Hz` `therefore C = 1/(X_(C).2pi) = (1/(100 XX 2pi xx (500)/pi)) = 10^(-4) F = 1 muF` |
|
| 44991. |
What should be the distance between the object in Exercise 9.24 and the magnifying glass if the virtual image of each square in the figure is to have an area of 6.25 mm^(2) . Would you be able to see the squares distinctly with your eyes very close to the magnifier? |
|
Answer» Solution :Magnification `=sqrt((6.25//1))=2.5` `v=+2.5u` `+(1)/(2.5u)-(1)/(u)=(1)/(10)` i.e., `u=-6cm` `|v|=15cm` The VIRTUAL image is CLOSER than the normal NEAR point (25 cm) and cannot be seen by the eye distinctly. |
|
| 44992. |
In a young ,s double slit experiment distance the slits is 1mm. The fringe width is found to be 0.mm. when the screen is moved through a distance of 0.25m away from the plane of the slit used . |
|
Answer» Solution : `BETA= 0.6xx10^(-3)m,beta_(2)=0.75xx10^(-3)m` `d= 1xx10^(-3)m, D_(1) = Dm, D_(2) = (D+ 0.25 ) m, lamda= ?` `beta_(1) = (lamdaD_(1))/(d) = (lamdaD)/(1xx10^(-3)) rightarrow(1)` `beta_(2)= ( lamda(D_(2)))/(d) = (lamda(D+0.25))/(1xx10^(-3)) rightarrow(2)` `beta-(1))/(beta_(2))= (0.6xx10^(-3))/(0.75xx10^(-3))= (lamdaD)/(lamda(D + 0.25))` `(D+ 0.25)0.6xx10^(-3)= 0.75xx10^(-3)D` `RightarrowD=1m` Subsituting the value of D in eqaution (1) or (2) `lamda= (beta_(1)d)/(D)= (0.6xx10^(-3)xx10^(-3))/(1)` `lamda=6xx10^(-7)m= 6000A^(@)` |
|
| 44993. |
A straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15 m/s and is directed perpendicular to the field. The e.m.f. induced between the two ends of the conductor is |
|
Answer» 0.10 V `epsilon = Blv` Here, `B=0.1 T, l=0.1 m, v = 15 ms^(-1), epsilon = ?` `epsilon =0.1xx0.1xx15=0.15 V` |
|
| 44994. |
Where gammarays are emited ? |
| Answer» Solution :The `gamma` rays are emitted from the nuclei of some RADIOACTIVE materials such as URANIUM,RADIUM etc. It was DISCOVERED by Paul ULRICH Villard. | |
| 44995. |
On metal surface radiation of 2000Å and 5000 Å is incident sequentially .Change in kinetic energy of photo-electric emitted during this will be…….h=6.6xx10^(-34)Js . |
|
Answer» 3.71 eV `K_(max)=(hc)/(lambda)-phi_(0)` `[because (1)/(2)mv_(max)^(2)=K_(max)` and `v=(c )/(lambda)]` In first case `(K_(max))_(1)=(hc)/(lambda_(1))-phi_(0)` In SECOND case `(K_(max))_(2)=(hc)/(lambda_(2))-phi_(0)` `THEREFORE DeltaK=(K_(max))_(1)-(K_(max))_(2)` `=6.6xx10^(-34)xx3xx10^(8)` `[(5xx10^(-7)-2xx10^(-7))/(5xx10^(-7)xx2xx10^(-7))]` `=6.6xx3xx10^(-26)xx(3xx10^(-7))/(10xx10^(-14))` `=59.4xx10^(-20)J` `=(5.94xx10^(-19))/(1.6xx10^(-19))eV` 3.7125 eV `~~3.71` eV |
|
| 44996. |
A boat which has a speed 5 km/h in still water crosses a river 100 m along the shortest possible path in 1.5 min. The velocity of river water in km/h is : |
|
Answer» 1 `|vec(V_(R))|=(OB)/t=0.1/(1.5/60)=60/15`=4km/h `vec(OA)` repesents velocity of man `:. AB=SQRT(OA^(2)-OB^(2))=sqrt(25-16)=3` `:.` Velocity of river =3km/h 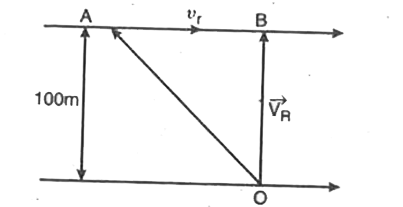
|
|
| 44997. |
In a choke coil, the values of reactance X_L and resistance R are such that |
|
Answer» `X_L = R` |
|
| 44998. |
Given a +b+c+d=0 which of the following statement is incorrect |
|
Answer» a,b,C and d must each be a null vector. |
|
| 44999. |
The range of a projectile, when launched at an angle of 15^@ with the horizontal is 1.5 km. The additional horizontal distance the projectile would cover when projected with same velocity at 45^@ is |
| Answer» ANSWER :C | |
| 45000. |
In the following circuit a 10m long potentiometer wire withresistance 1.2 ohm/m , a resistance R 1 and an accumulator of emf 2 V are connected in series. When the emf of thermocouple is 2.4 mV then the deflection in galvanometer is zero. The current supplied by the accumulator will be |
|
Answer» `4 XX 10^(–4) A` |
|