Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

2501.

Explain Malus law and write it.

Answer»

Solution :If the pass-axis of `P_(2)` makes an angle `theta` with the pass-axis of `P_(1)` then `VECE` vectors `(E_(0))` emerging from `P_(2)` makes an angle `theta` with pass axis of polaroid `P_(1)` which is shown in the FIGURE.
By taking two component of vector `E_(0)` of plane POLARIZED light,
(1) `E_(0)costheta` which is parallel to pass-axis of analyser `P_(1)`.
`E_(0)SINTHETA` which is perpendicular to pass-axis of analyser `P_(1)`.

Component `E_(0)costheta` passes through `P_(1)` while component `E_(0)sintheta` is perpendicular to pass-axis of `P_(1)` so it is absorbed.
Now intensity of light is proportional to square of amplitude intensity of light incident on analyser is `I_(0)propE_(0)^(2)` and intensity of light emerging from analyser is `Iprop(E_(0)costheta)^(2)`.
Hence, intensity of light emerging from analyser,
`(I)/(I_(0))=(E_(0)^(2)cos^(2)theta)/(E_(theta^(2)))=cos^(2)theta`
`:.I=I_(0)cos^(2)theta`
This is known as Malus law.
Discussion
2502.

The best waves for emission of electrons from a surface :

Answer»

Microwaves
Ultra VIOLET rays
Infrared rays
X-rays.

Answer :D
Discussion
2503.

The position x of a particle at time t is given by : x=(v_(0))/(a)(1-e^(-at)) where v_(0) is a constant and a>0. The dimensional formula of v_(0) and a is :

Answer»

`[M^(0)LT^(-1)]` and `[T^(-1)]`
`[M^(0)LT^(0)]` and `[T^(-1)]`
`[M^(0)LT^(-1)]` and `[T^(-2)]`
`[M^(0)LT^(-1)]` and `[T]`

Solution :Here exponential has no DIMENSION.
THUS `at=M^(0)L^(0)T^(0)`
`a=(1)/(T)=T^(-1)`
Also `v_(0)/(a)=x=L^(1)`or `v_(0)=aL^(1)`
`:.v_(0)=LT^(-1)`
Hence correct CHOICE is `(a)`.
Discussion
2504.

When a high-speed passenger train traveling at 161 km/h rounds a bend, the engineer is shocked to see that a locomotive has improperly entered onto the track from a siding and is a distance D=676 m ahead ( Fig. 2-20). The locomotive is movingat 29.0 km/h. The engineerof the high-speed train immediately applies the brakes . (a) What must be the magnitude of the resulting constant deceleration if a collision is to be justavoided ? (b) Assume that the engineer is at x=0 when , at t=0, he first spots the locomotive. Sketch x(t) curves for the locomotive and high-speed train for the cases in which a collision is just avoided and is not quite avoided.

Answer»


ANSWER :(a) `-0.994 m//s^(4)`
Discussion
2505.

What is the amount of magnetic flux density at the axial line of magnetic dipole.

Answer»

SOLUTION :`B=mu_0/(4PI).(2MU)/d^3`
Discussion
2506.

Two bodies of masses m_(1) and m_(2) are separated by a distance R. The distance of the centre of mass of the bodies from the mass m_(1) is

Answer»

`(m_(2)R)/(m_(1)+m_(2))`
`(m_(1)R)/(m_(1)+m_(2))`
`(m_(1)m_(2))/(m_(1)+m_(2))R`
`(m_(1)+m_(2))/(m_(1))R`

SOLUTION :Consider MASS `m_(2)` is at the origin.
Centre of mass of the SYSTEM
`X_(EM)=(m_(1)xx0+m_(2)xxR)/(m_(1)+m_(2))`
`=(M_(2)R)/(m_(1)+m_(2))`
Discussion
2507.

The total magnetic induction at point O due to curved portion and straight portion in the following figure, will be

Answer»

`(mu_(0)i)/(2pir)[pi-phi+tanphi]`
`(mu_(0)i)/(2pir)`
0
`(mu_(0)i)/(PIR)[pi-phi+tanphi]`

ANSWER :A
Discussion
2508.

The principle made use of an lightning arrester is .................. .

Answer»


ANSWER :ACTION of POINTS
Discussion
2509.

James Clerk Maxwell modified Ampere.s circuital theorem by introducing the concept of displacement current. : What do you mean by displacement current?

Answer»

SOLUTION :The current DUE to time varying electric FIELD is CALLED DISPLACEMENT current.
Discussion
2510.

How we define mutual-inductance?

Answer»

SOLUTION :It is defined as the magnetic flux through one coil DUE to the flow of one ampere CURRENT in the neighboring coil.
M = `phi_2/I_1` where I_1 = Current FLOWING through a coil.
`phi_2` = Magnetic flux linked with other coil.
Discussion
2511.

A : The apparent depth of a tank of water decreases if viewed obliquely. R : Real depth decreases if viewed obliquely.

Answer»

If both ASSERTION & Reason are TRUE and the reason is the CORRECT explanation of the assertion, then mark (1).
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark (2).
If Assertion is true statement but Reason is false, then mark (3).
If both Assertion and Reason are false statements, then mark (4).

Answer :C
Discussion
2512.

An ideal p-n junction is to be used across a battery of 3 V. A resistance of ______ should be connected in series of p-n junction so as to limit the current to 15 mA only.

Answer»

Solution :200 `OMEGA , 15` mA ` = (3 V)/(R) RARR R = 200 Omega`
Discussion
2513.

A thin insulating rod of mass m and length L is hinged at its upper end (O) so that it can freely rotate in vertical plane. The linear charge density on the rod varies with distance (y) measured from upper end as {:(lamda=ay^(2),0 le y le (L)/(2)),(=-by^(n),(L)/(2)ltyleL):}} Where a and b both are positive constants. whenahorizontal electric field E is switched on the rod is found to remains stationary. (a). find the value of constant b in terms of a. Also find n. (b). Find the force applied by the hinge on the rod, if EaL^(3)=45mg.

Answer»


Answer :(a) `B=(a)/(15);n=2`
(b). `SQRT(2)MG`
Discussion
2514.

Object #1 moves toward object #2, whose mass is twice that of object #1 and which is initially at rest. After their impact, the object lock together and move with what fraction of object #1's initial kinetic energy?

Answer»

`(1)/(18)`
`1/9`
`1/6`
`1/3`

Solution :FIRST, apply conservation of linear momentum to calculate the speed of the COMBINED object after the (perfectly inelastic) collision.
`m_(1)v_(1)+m_(2)v_(2)=(m_(1)+m_(2))v'`
`v'=(m_(1)v_(1)+m_(2)v_(2))/(m_(1)+m_(2))` LTBRGT `=(m_(1)v_(1)+(2m_(1))(0))/(m_(1)+2m_(1))`
Therefore, the ratio of the kinetic energy after the collision to the kinetic energy before the collision is
`(K')/(K')=((1)/(2)m'v^('2))/((1)/(2)m_(1)v_(1)^(2))=((1)/(2)(m_(1)+2m_(1))((1)/(3)v_(1))^(2))/((1)/(2)m_(1)v_(1)^(2))=(1)/(3)`.
Discussion
2515.

Eleven equal point charges, all of then having a charge +Q , are placed at all the hour positions of a circular clock of radius r, except at the 10 hour position . What is the electric field strength at the centre of the clock ?

Answer»

`(Q)/(4piepsilon_(0)r^(2))` from the CENTRE towards the mark 10
`(Q)/(4piepsilon_(0)r^(2))` from the mark 10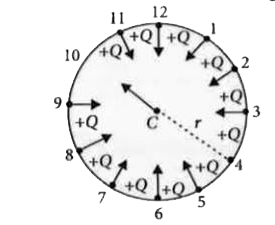towards the centre
`(Q)/(4piepsilon_(0)r^(2))` from the centre towards the mark 6
Zero

Solution :Given,radius of the circular clock = r and each of ELEVEN position of a circular clock has a charge +Q.

`THEREFORE` Electric field at the centre of the clock is
`E_(0)=E_(1)+E_(2)+E_(3)+E_(4)+E_(5)+E_(6)+E_(7)+E_(8)+E_(9)+E_(10)+E_(11)+E_(12)`
Now , `E_(1)andE_(7)`are opposite to each other , so they will cancel out each OTHERS effect.
Similarly`E_(2)andE_(8),E_(3)andE_(9),E_(5)andE_(11),E_(6)andE_(12)`will also cancel out their effect as they are opposite to each other.
`thereforeE_(c)=E_(4)=(1)/(4piepsilon_(0))(Q)/(r^(2))` (directed from the centre towards the maek 10)
Discussion
2516.

The diameter of a wire as measured by a screw gauge was found to be 1.002cm, 1.000cm, 1.006cm. The absolute error in the Secondreading is

Answer»

`0.002` CM
`0.004 cm `
`0.006 cm `
`0.003 cm `

ANSWER :D
Discussion
2517.

The resistance of a conductor at 20 ^@C"is" 6.3 Omega and "at" 100^@C it is 7.5 Omega . Calculate the resistance of the conductor at 0^@C and its temperature coefficient of resistance .

Answer»

Solution :Temperature dependence of resistance is given by `R= R_(0) (1 + alpha t)`. On SUBSTITUTING values we can write the following :
`6.3= R_(0) (1 + 20 alpha)` …(i)
`7.5 = R_(0) (1 + 100 alpha)` …(ii)
Divding equations (i) and (ii) we get
`(6.3)/(7.5) = (1 + 20 alpha)/(1 + 100 alpha) rArr 6.3 + 630 alpha = 7.5 + 150 alpha`
`rArr 480 alpha = 1.2 rArr alpha = (1.2)/(480) = 0.0025" PER " ""^(@)C`
On substituting calculated `alpha` in equation (i) we get
`R_(0) = (6.3)/(1 + 20 alpha) = (6.3)/(1 + 20 xx 0.0025) = 6 Omega`
Discussion
2518.

Susceptibility of a diamagnetic substance has a value

Answer»

`GT 1 `
`1`
`LT 1 `
`lt 0`

SOLUTION :`lt 0`
Discussion
2519.

A flywheel of mass 4 kg has radius of gyration 0.4m . calculate the kinetic energy of rotation when it makes 5 r.p.s.

Answer»

531.8 J
315.8 J
325.8 J
None

Answer :C
Discussion
2520.

For a single slit of width "a", the first minimum of the interference pattern of a monochromatic light of wavelength lambda occurs at an angle of (lambda)/(a). At the same angle of (lambda)/(a), we get a maximum for two narrow slits separated by a distance "a" . Explain.

Answer»

Solution :In the first case, the OVERLAPPING of the contributions of the wavelets from TWO halves of a SINGLE slit produces a minimum because CORRESPONDING wavelets from two halves have path difference of `(lambda)/(2)`.
In the second case, the OVERLAPING of the wave fronts from the two slits produces first maximum because these wave fronts have the path differences of `lambda`.
Discussion
2521.

In YDSE fringes are obtainedusinglight of wavelength 4800 A^(0).One slitis covered with a thinglass filmof refractive index1.4 and anotherslit iscoveredby a filmof samethickness but refractive index 1.7.By doing so the centrafringeis shiftedto fifth bright in the original pattern. Thethickness of glassfilm isx xx 10^(-3) mm, what is the value of x ?

Answer»


ANSWER :8
Discussion
2522.

The increasing order of the specific charge on (i) electron (e) (ii) proton (p) (iii) neutron (n) and (iv) O-particle (a) is :

Answer»

<P>`E,p,N,ALPHA`
`n,p,e,alpha`
`n,p,alpha,e`
`n,alpha,p,e`

ANSWER :D
Discussion
2523.

Frost uses the image of two diverging roads to symbolize...

Answer»

SORROW and regret
Life's choice
The LOVE of nature
The SPIRIT of independence

Answer :B
Discussion
2524.

Given that the horizontal and vertical components of earth are equal at a place. What is the angle of dip at that place ?

Answer»

Solution :When the horizontal and vertical components of the earth.s MAGNETIC field are equal, we have
`B COSTHETA= B sintheta`
where B is TOTAL intenwsity of earth.s magnetic field and `theta` is the angle of DIP.
Discussion
2525.

Two charges of magnitudes -2Qand+Q are located at points (a,0)and(4a,0) respestively . Whatis the electric flux due to these charges through a sphere of radius 3a with its centre at the origin ?

Answer»

Solution :Gauss .s theorem states that the ELECTRIC FLUX through a closed suface enclosing charges is equal to `(1)/(epsilon_(0))`times the magnitude of the charge enclosed.
The SPHERE enclosed a charge of `-2Q`,so
`phi=(2Q)/(epsilon_(0))`
Discussion
2526.

When one computes the square root of the ratio of the permeability of free space to the permitivity of free space, one obtains sqrt(mu_(0)/epsilon_(0))=337. What is the unit of this quantity?

Answer»

farads
joules
volts
ohms

SOLUTION :Unit of `mu_(0)`= ohm sec/meter
`C^(2) = 1/(mu_(0)epsilon_(0))`
`RARR epsilon_(0) = 1/(C^(2) mu_(0))`
C=velocity of light
`xsqrt(mu_(0)/epsilon_(0)) = SQRT(mu_(0)^(2)C^(2))= mu_(0)C`
Unit of C = metre/sec.
Unit of `sqrt((mu_(0))/epsilon_(0)) =` unit of `mu_(0)C`= ohm sec/meter x meter/sec = Ohm.
Discussion
2527.

In a Young's double slit experiment, the angular width of a fringe formed on distance screen is 0.1^(@).The wvae length of light find spacing between the slit.

Answer»

`3.4 xx 10^(-6) m`
`4.3 xx 10^(-4) m`
`4.3 xx 10^(-6) m`
`3.4 xx 10^(-4) m`

Solution :Using the relation , `theta = (beta)/(D)` and putting `beta = (D LAMBDA)/(d)`, we get `theta = (Dlambda)/(DD) = (lambda)/(d)`
or `d = (6000 xx 10^(-10))/((pi)/(180) xx 0.1) = (6000 xx 180 xx 10^(-10))/(pi xx 0.1)`
`THEREFORE` Spacing between `d = 3.44 xx 10^(-4) m`. Angular fringe width is independent of the distance between screen and PLANE of slits i.e. D.
Discussion
2528.

At what temperature will the average K.E. per molecule of a gas be exactly half its value at N.T.P. ?

Answer»

`136.5^@K`
`120^@K`
`125.5^@K`
None

Answer :A
Discussion
2529.

What is electromagnetic spectrum?

Answer»

Solution :`GAMMA`-rays, x-rays, Radio WAVES, infraed LIGHT and MICROWAVES.
Discussion
2530.

An ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is

Answer»

`(4mg)/(K)`
`(2MG)/(k)`
`(Mg)/(k)`
`(Mg)/(2k)`

ANSWER :B
Discussion
2531.

What should be the current in a circular coil of radius 5cm to annual B_(H)=5xx10^(-5)T

Answer»

`0.4A`
`4A`
`40A`
`1A`

ANSWER :B
Discussion
2532.

What happens if intensity of light is increased, when the frequency is less than threshold value?

Answer»

SOLUTION :PHOTOELECTRIC EMISSION is not POSSIBLE.
Discussion
2533.

Two capacitors of a capacitance 3 mu Fand 6mu F respectively are connected in series across a 100 V power supply. Charge on each capacitor is _____________ .

Answer»

Solution :`200 muC`. RESULTANT CAPACITANCE `C_s = (C_1 C_2)/(C_1+C_2) = ((3 xx6))/((3 + 6)) MU F = 2muF `
`:.` CHARGE `Q =C_s. V= 2 MUF xx 100 V= 200 muC`
Discussion
2534.

Obtain equation for force between two parallel currents carrying wire.

Answer»

Solution :1. Two long wire a and b are placed at d distance apart from each other and `I_(a)andI_(b)` current flowing through them.

2. The conductor .a. produces the same magnetic field `vecB_(a)` at all points along the conductor .b..
3. The right hand rule tells US that the direction of this field is downwards. (When the conductor are placed horizontally).
`B_(a)=(mu_(0)I_(a))/(2pid)""...(1)`
4. The conductor .b. CARRYING a current `I_(b)` will experience a sideways force DUE to the field B. The direction of this force is towards the conductor .a..
Force on wire is given by `vecF=IveclxxvecB`
`F_(ba)=(I_(b)L)B_(a)`
`F_(b_(a))=(mu_(0)I_(a)I_(b)L)/(2pid)""...(2)`
5. It is of course possible to compute the force on .a. due to .b.. From consideration SIMILAR to above we can find the force `F_(ab)` on a segment on a segment length L of .a. due to the current in .b.. It is equal in magnitude to `F_(ba)` and directed towards .b Thus,
`vecF_(ba)=-vecF_(ab)""...(3)`
6. This is consistent with Newton.s third law.
7. We have seen from above that currents flowing in the same direction attract each other. One can show that oppositely directed currents repel each other.
8. Thus, parallel currents attract and antiparallel currents repel.
Discussion
2535.

(a) Two cells of emfe and € have their internal resistances epsi_(1) and epsi_(2) respectively. Deduce an expression for the equivalent emf and internal resistance of their parallel combination when connected across an external resistance R. Assume that the two cells are supporting each other. (b) In case the two cells are identical, each of emf e= 5V and internal resistance r= 2Omega, calculate the voltage across the external resistance R= 10Omega.

Answer»

Solution :(a). Consider a parallel combination of two cells. Let `epsi_(1) and epsi_(2)` be the emfs of two cells and `r_(1) and r_(2)` their respective INTERNAL RESISTANCES. `I_1 and I_2` are the currents leaving the positive ELECTRODES of two cells and at Junction `B_1`, these currents are added up so that net CURRENT
`l=l_(1)+l_(2)` ..........(i)
Let `V(B_1) and V(B_2)` be the potentials at `B_1 and B_2,` respectively, then considering first cell, we have
`V=V(B_(1))-V(B_(2))=epsi_(1)-l_(1) r_(1) rArr l_(1)=(epsi_(1)-V)/(r_(1))` ............(ii)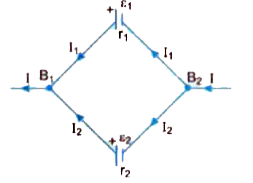

and considering second cell, we have
`V=V(B_(1))-V(B_(2))=epsi_(2)-l_(1) r_(2) rArr l_(2)=(epsi_(2)-V)/r_(2) ..........(iii)`
`l=l_(1)+l_(2) =(epsi_(1)-V)/(r_(1))+(epsi_(2)-V)/(r_(2)) =(epsi_1/r_1+epsi_2/r_2)-V(1/r_(1)+1/r_(2))`
`rArr V=[(epsi_1/r_1+epsi_2/r_2) -I]//(1/r_(1)+1/r_(2))=((epsi_(1)r_(2)+epsi_(2)r_(1))/(r_(1)+r_(2))-I (r_(1)r_(2))/(r_(1)+r_(2))` .......(iv)
If instead of two cells we join a single cell having equivalent emf `e_(eq)` and equivalent internal resistance `e_(eq)` then we have
`V=epsi_(eq)-I r_(eq)` .........(v)
Thus, comparing (iv) and (v), we get
`e_(eq)=(epsi_(1)r_(2)+epsi_(2)r_(1))/(r_(1)+r_(2)) and r_(eq)=(r_(1)r_(2))/(r_(1)+r_(2))`
Alternately, we can write
`1/r_(eq)=1/r_(1)+1/r_(2) and (epsi_(eq))/(r_(eq))=epsi_1/r_1+epsi_(2)/r_(2)`
(b) As per question emf of cells `epsi_(1)=epsi_(2)=5V`, internal resistance of cells `r_(1)=r_(2)=2 Omega` and external resistance R=10 V.
Effective emf of cell combination `epsi=(epsi_(1)r_(2)+epsi_(2)r_(1))/(r_(1)+r_(2))=(5 xx 2 +5 xx 2)/(2+2)=5V`
and effective internal resistance `r=(r_(1)r_(2))/(r_(1)+r_(2))=(2 xx 2)/(2+2) =1 Omega`
Current in the circuit `I=epsi/(R+r)=(5)/(10+1)=5/(11) A`
Voltage across external resistance, `V=IR=(5)/(11) xx 10=4.55V`
Discussion
2536.

A cannon and a larger are 5.10 km apart and located at the same level. How soon will the shell launched with the initial velocity 240 m/s reach the farger in the absence of air drag?

Answer»

Solution :Here `v_(0)=240 ms^(-1) , R =5.10 km =5100 m`
`g=9.8 ms^(-2), ALPHA= ? "" R=(v_(0)^(2) 2 alpha)/(g)`
`sin 2 alpha=(Rg)/(v_(0)^(2)) "" rArr alpha=30^(@) or 60^(@)`
Using =`T=(2v_(0) sin alpha)/(g)`
When `alpha=30^(@), T_(1)=(2xx240xx0.5)/(9.8)=24.5s`
When `alpha=60^(@)T_(2)=(2xx240xx0.867)/(9.8)=42.41s`
Discussion
2537.

The period of oscillation of a magnet of a vibraion magnetometer is 2.45 s at one place and 4.9 s at the other, the ratio of the horizontal component of earth magnetic field at the two places is

Answer»

`1:4`
`1:2`
`2:1`
`4:1`

ANSWER :D
Discussion
2538.

Three planets of same density and with radiiR_1,R_2 and R_3such that R_1=2R_2=3R_3have gravitation fields strength on planets arev_1,v_2,v_3, respectively. Then :

Answer»

`g_1//g_2=1//2`
`g_1//g_3=3`
`v_1//v_2=2`
`v_1//v_3 =1//3`

Solution :`v=sqrt(2QR)=sqrt((2GM)/R)=sqrt((2G)/R(rho4/3piR^3))=sqrt((8piGP)/3)R`
Therefore , `rArr v_1/v_2=R_1/R_2 =2 , g_1/g_2=3 , g_1/g_3=R_1/R_3=3 , v_1/v_3=R_1/R_3=3`
`G=(GM)/R^2 =G/R^2 (rho 4/3 piR^3) =(5piGP)/3 R`
Discussion
2539.

How many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit ?

Answer»

Solution :`q = Q(1-e^-n)`
` 2q^2/2C = initial VALUE `
` q^2/2C = final value`
` rArr 2q^2/2C = q^2/2C`
` rArr q^2 = q^2/2rArr q= (SQRT (q^2/2))`
` rArr q/(sqrt 2) = q(1-e^-n)`
` rArr 1/sqrt 2 = 1-e^-n`
` rArr e^-n = 1 - (1/sqrt(2)) = ((sqrt(2))-1/sqrt(2))`
` rArr n= log ( sqrt(2) / ((sqrt 2)-1))` = 1.22 `
Discussion
2540.

Which statement is correct for intermediates.

Answer»

METHYL carbocation isplanar and has incomplete octet.
Phenyl carbocatio is resonance stabilised cation.
Phenyl carbanion is PLANAR but not resonance stabilised.
Methyl carbocation is stabilised by hyperconjugation AFFECT of three hydrogen atoms.

Solution :FACT base.
Discussion
2541.

The velocity at the maximum height of a projectile is half of its initial velocity of projection The angle of projection is

Answer»

`30^(@)`
`45^(@)`
`60^(@)`
`76^(@)`

Answer :C
Discussion
2542.

A monoenergetic (18 keV) electron beam initially in the horizontal direction is subjected to a horizontal magnetic field of 0.04G normal to the initial direction. Estimate the up or down deflection of the beam over a distance of 30 cm (m_(e) = 9.11 xx 10^(-31)kg). [Note : Data in this exercies are so chosen that the answer will give you an idea of the effect of earth's magnetic field onthe motion of the electron beam from electron gun to the screen in a TV set].

Answer»

Solution :Here energy E `= 18 KEV = 18 XX 1.6 xx 10^(-19)J`
`B = 0.40 G = 0.40 xx 10^(-4)T`
`x = 30 cm = 0.3 m`
As `E = (1)/(2) mv^(2) :. v = sqrt((2E)/(m))`
In magnetic field electron beam is deflected along a circular arc or radius r, such that
`BeV = (mv^(2))/(r)` or `r = (mv)/(Be)`
`r = (m)/(Be)sqrt((2E)/(m)) = (1)/(Be) sqrt(2Em) = 11.3 m`
If y is the deflection at the END of the path it is clear from FIG.
`theta = (x)/(r) = (y)/(x//2) = 2(y)/(x)`
or `y = (x^(2))/(2r) = (0.30 xx (0.30))/(2 xx 11.3)m = 0.004 m = 4mm`
Discussion
2543.

Light from a source falls on a straight edge at a distance of 50 cm and the didtance between the first and third maxima is found to be 1.197 mm on a screen at a distance 75 cm from the edge. Calculate wavelength of light falling on the slit.

Answer»

SOLUTION :5002 Å
Discussion
2544.

Determine V_(0) and I for the networks of figure.

Answer»

SOLUTION :(a) `V_(0)` =9.7V,I=9.7mA,
(B)`V_(0)` =14.6V,I=0.553mA
Discussion
2545.

The volume of a gas and the number of gas molecules within that volume for four situations are (1) 2V_(0)andN_(0) (2) 3V_(0)and3N_(0) (3) 8V_(0)and4N_(0) (4) 3V_(0)and9N_(0) Which of them has mean free path greatest?

Answer»

1
2
3
4

Solution :Mean free PATH, `lambda=(1)/(SQRT(2)pid^(2)n)n=(N)/(V)`, which is GREATEST for least value of n.n is least in case (a) and (C ).
Discussion
2546.

In a radioactive decay, an element ""_(z)X^A emits four alpha- particles, three beta -particles and eight gamma photons. The atomic number and mass number of the resulting final nucleus are

Answer»

Z-8, A-13
Z-11, A-16
Z-5, A-13
Z-5, A-16

Solution :After `n_(a), alpha`- DECAYS and `n_(BETA) beta`- decays, the respective atomic number and mass number of resulting nucleus are GIVE by
`Z.=Z-2_(n_(alpha))=Z-8+3=Z-5`
and `A.=A-4n_(alpha)=A-16`
Discussion
2547.

Two equal resistances are connected in the gaps of a metre bridge. If the resistance in the left gap is increased by 10%, the balancing point shirt

Answer»

`10%`to RIGHT
`10%` to LEFT
`9.6%` to right
`4.8%` to right

Answer :D
Discussion
2548.

In the Boolean expression bar(A).bar(B) is equal to

Answer»

A+B
`BARA +BARB`
`BAR(A.B)`
`bar(A+B)`

ANSWER :D
Discussion
2549.

Angle of the prism A = 72^(@) and its refractive index is 1.66 the prism is immersed in a liquid of refractive index 1.33 Find the angle of minimum deviation for a parallel beam of light passing through the prism .

Answer»


ANSWER :`22^(@)`22'
Discussion
2550.

The Young's modulus of a certain material is 24 xx 10^11 "dyne"/(cm^2) . Within what range the value of rigidity modulus must lie ? (sigma = 0.5)

Answer»

a)`8 xx 10^11"dyne"/(cm^2)`
B)`9 xx 10^11"dyne"/(cm^2)`
C)`8.5 xx 10^11"dyne"/(cm^2)`
d)`10 xx 10^11"dyne"/(cm^2)`

ANSWER :A
Discussion