Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

39601.

A charged ball of mass 9 kg is suspended from a string in a uniform elelctric field vecE = (3hati + 5hatj) xx 10^5 N//C. The ball is in equilibrium with theta=37^@. If direction of electric field is reversed, fing the new equilibrium position of the ball. Given your answer in terms of angle made by string with vertical. Take g = 10ms^(-2).

Answer»

`TAN^(-1)(3/4)`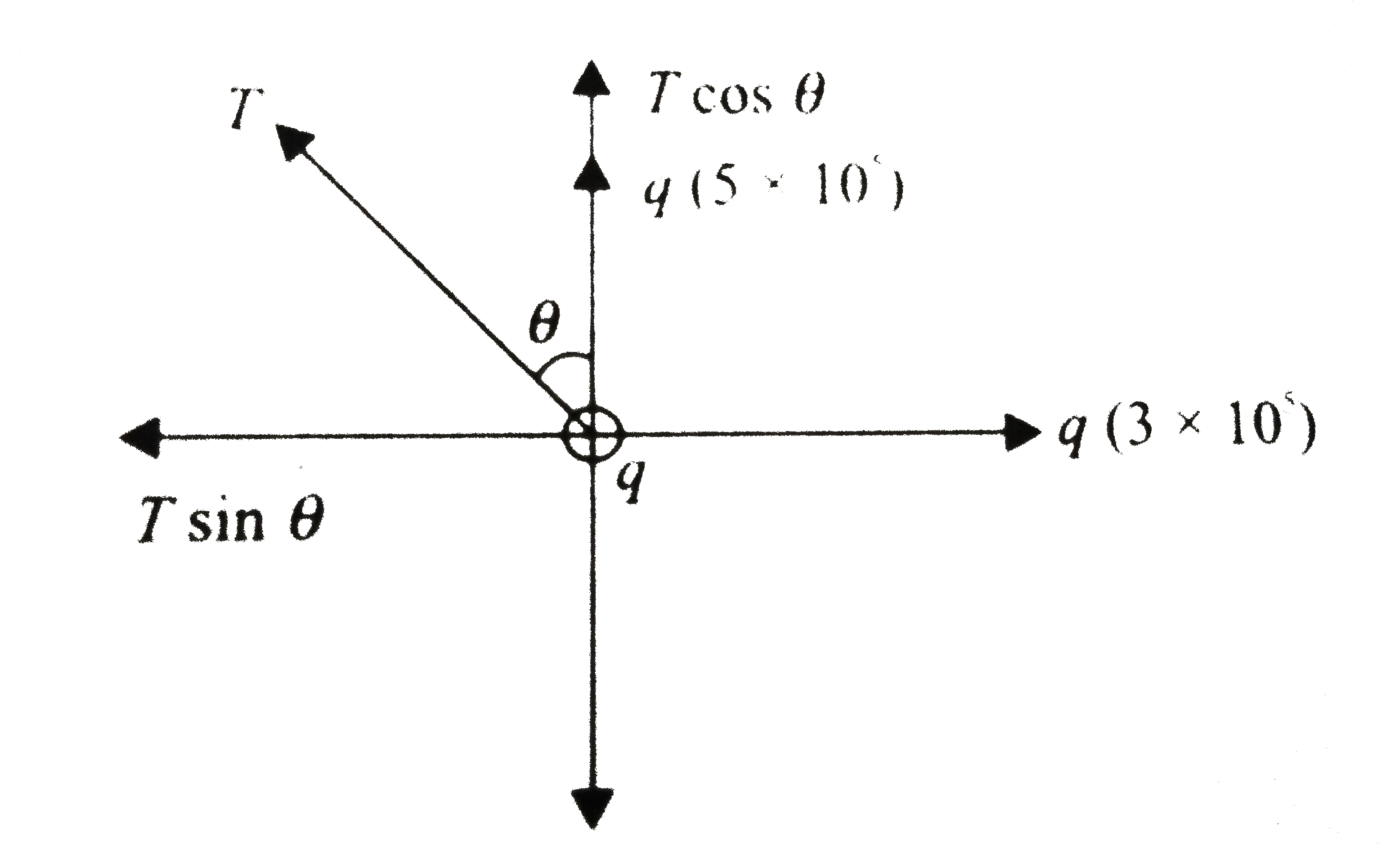
`cot^(-1) (3/14)`
`cot^(-1) (3/4)`
`tan^(-1)(3/14)`

Solution :
`Tsin theta=3thetaxx10^(5)`(i)
`Tcostheta=mg-5qxx10^(5)`(ii)
Solve to get `q=100muC,T=50N`.
After the rever4sal of direction of electric FIELD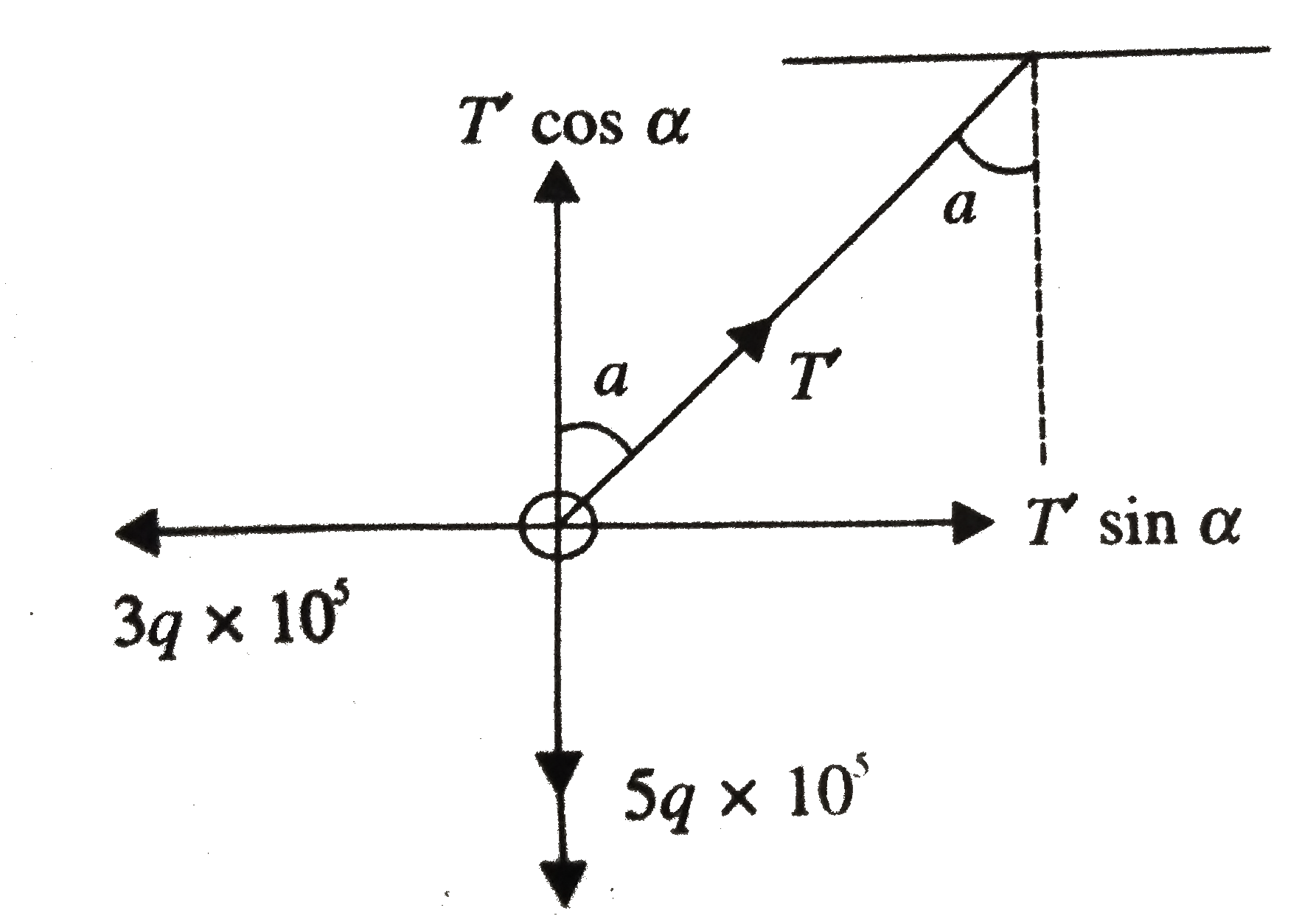

`T'sin a=3qxx10^(5)` or `T'cos a=mg+5qxx10^(5))`
`TANA=(3qxx10^(5))`
`=(3XX10^(-4)xx10^(5))/(9xx10+5xx10^(-4)xx10^(5))=(3)/(14)`
or `a=tan^(-1)((3)/(14))`
Discussion
39602.

(A) : We do not feel the pressure when sun shines on our hand even the energy being absorbed from the EM waves (Our hands get warm). (R) : EM waves transfer momentum to our hands but because speed of light is very large so the momentum transfered is very small.

Answer»

Both 'A' and 'R' are TRUE and 'R' is the CORRECT EXPLANATION of 'A'.
Both 'A' and ’R' are true and 'R' is not the correct explanation of 'A
A' is true and 'R' is FALSE
'A' is false and R' is true

Answer :A
Discussion
39603.

A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, (a) the wire intersects the axis, (b) the wire is turned from N-S to northeast-northwest direction, (c) the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?

Answer»

SOLUTION : (a) 2.1 N VERTICALLY DOWNWARDS (b) 2.1 N vertically downwards (true for any ANGLE between CURRENT and direction and B since l sin `theta `remains fixed, equal to 20 cm) (c) 1.68 N vertically downwards
Discussion
39604.

Figure shows a ray of light passing through a prism. If the refracted ray QR is parallel to the base BC, show that (i) r_(1) = r_(2) = A//2, (ii) angle of minimum deviation, D or D_(m) = 2i -A.

Answer»

SOLUTION :(i) From give figure, `A = r_(1) + r_(2)`
As RAY QR is parallel to the base BC,
then `r_(1) = r_(2)`, and i = E
Therefore, `2r_(1) ` ( or `2r_(2)) = A`
`rArr r_(1) = r_(2) = A//2`
(ii) `D = x+y``D = ( i - r_(1)) + ( e- r_(2))`
`D = ( i +e ) - ( r_(1) + r_(2))`
or`D = 2i -A`
Discussion
39605.

The axes of the poariser and analyser are inclined to each other at 60^(@). If the amplitude of polarised light emergent through analyser is A. The amplitude of unpolarised light incident on polariser is

Answer»

`A"/"2`
`A`
`2A`
`2sqrt(2)A`

ANSWER :D
Discussion
39606.

The figure shows the electric field lines in the vicinity of two point charges. Which one of the following statements concerning this situation is true ?

Answer»

`q_1` is negatuve and `q_1` is POSITIVE
The magnitude of RATIO `(q_2//q_1)` is LESS than one
Both `q_1` and `q_2` havve the same SIGN of charge

The electric field is strongest midway between the charges

Solution :Since field line are originating gron ` q_1` and terminating at ` q_2` to ` q_1` is lessthab ` q_1` so ` q_2 //q_1 lt 1`.
Discussion
39607.

An electron is in a certain energy state in a one- dimensional, infinite potential well from x = 0 to x = L = 180 pm. The electron's probability density is zero at x = 0.300L, and x = 0.400L, it is not zero at intermediate values of x. The electron then jumps to the next lower energy level by emitting light. What is the change in the electron's energy?

Answer»

SOLUTION :`3.54xx10^(-17)J`
Discussion
39608.

To help keep his warm on cold days, a farmer stores 840 kg of solar-heated water ( L_(F) = 3.35 xx 10^(5) J //kg ) in barrels . For how many hours would a 2.0 kW electric space heater have to operate to provide the same amount of heat as the water does when it cools from 10.0 to 0.0^(@)C and completely freezes ?

Answer»


ANSWER :44
Discussion
39609.

A : An inductor and a capacitor are called low pass filter and high pass filter respectively. R : Reactance of an inductor is low for low frequency signals and that of a capacitor is high for high frequency signals.

Answer»

If both Assertion & Reason are TRUE and the reason is the CORRECT explanation of the assertion, then mark (1)
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark (2)
IfAssertion is true statement but Reason is FALSE, then mark (3)
If both Assertion and Reason are false statement, then mark (4)

ANSWER :C
Discussion
39610.

The equation of alternating current for a circuit is given I = 50 cos 100 pi t. Find (i) frequency of a.c. applied (ii) mean value of current during positive half of the cycle (iii) virtual value of current and (iv) the value of current 1/300 sec after it was zero

Answer»


Answer :(i) 50 HZ, (II) 31.8 A, (III) 35.35 A, (iv) 43.3 A
Discussion
39611.

A particle of mass m is tied to a light string and rotated with a speed v along circular path of radius r. If T is tension in the string and mg is gravitational force on the particle then, the actual forces acting on the particle are

Answer»

MG, and T only
mg, T and an ADDITIONAL FORCE of `(mv^(2))/(r )` directed inwards
mg. T and an additional force of `(mv^(2))/(r )` directed outwards
only a force `(mv^(2))/(r )` directed outwards

Answer :A
Discussion
39612.

An oscilllator of frequency 680 Hz drives two speakers. The speakers are fixed on a vertical pole at a distance 3m from each other as shown in the fig. A person whose height is almost the same as that of the lower speaker walks towards the lower speaker in a direction perpendicular to the pole. Assuming that these is no reflection of sound from the ground and speed of sound is v = 340 m/s. How far is the person from the pole when he hears a minimum in sound intensity a second time ?

Answer»

5.6 m
7.8 m
12.4 m
17.6m

Answer :A
Discussion
39613.

An oscilllator of frequency 680 Hz drives two speakers. The speakers are fixed on a vertical pole at a distance 3m from each other as shown in the fig. A person whose height is almost the same as that of the lower speaker walks towards the lower speaker in a direction perpendicular to the pole. Assuming that these is no reflection of sound from the ground and speed of sound is v = 340 m/s. As the person walks toward the pole, his distance from the pole when he first hears a minimum in sound intensity is nearly

Answer»

14.6 m
17.9 m
10.1 m
22.4 m

Answer :B
Discussion
39614.

A stationary Pb^(200) nucleus emits an alpha-particle with kinetic energy T_(alpha)= 5.77MeV. Find the recoil velocityof a daughter nucleus. What friction of the total energy liberated in this decay is accountd for by the recoil energy of the daughter nucleus?

Answer»

Solution :The momentum of the `alpha`-particle is
`sqrt(2M_(alpha)T)`. This is also the recoil momentum of the daughter nuclear in opposite DIRECTION.
The recoil VELOCITY of the daughter nucleus is
`(sqrt(2M_(alpha)T))/(M_(d))=(2)/(196)sqrt((2T)/(M_(p)))= 3.39xx10^(5)m//s`
The ENERGY of the daughter nucleus is `(M_(alpha))/(M_(p))T` and this represents a fraction
`(M_(alpha)//M_(d))/(1+(M_(alpha))/(M_(d)))=(M_(alpha))/(M_(alpha+M_(d)))=(4)/(200)=(1)/(50)=0.02`
of total energy. Here `M_(d)`is the mass of the daughter nucleus.
Discussion
39615.

A parallel plate capacitor with circular plates of radius 1m has a capacitance of 0.5muF. At t=0, it is connected for charging inseries with a resistance R=2kOmega across a 4V battery. Calculate the magnetic field at a point P in between the plates and half way between the centre and periphery of the plates after 10^-3s. Fig.

Answer»

<P>

Solution :Here, `r=1m, C=0.5muF =0.5xx10^-6F,`
`R=2kOmega=2xx10^3Omega,V=4V,t=10^-3s`.
The charge Q on the capacitor at any time t during
charging is
`Q=Q_0(1-e^(-t//RC))=CV(1-e^(-t//RC))`
`:. (dQ)/(dt)=CVxx1/(RC) e^(-t//RC)=V/R e^(-t//tau) ( :' tau=RC)`
Electric field in between the plates at time t is
`E=Q/(in_0A) =Q/(in_0pir^2)`
`(dE)/(dt)=1/(in_0pir^2) (dQ)/(dt) =1/(in_0pir^2)xxV/R e^(-t//tau)`
Let us now consider a circular loop of radius
`r'=(=1/2m)`, parallel to the plates passing
through P. The magnetic field B at all points on
this loop is of the smae value and acting
tengentially to the loop.
Applying Ampere Maxwell's Law to this loop,
we get
`oint vecB.vec(dl)=mu_0[I+in_0 (dphi_E)/(dt)]`
or `B2pir'=mu_0(0+in_0pir' (dE)/(dt))`
or `B=mu_0(in_0r')/2 (dE)/(dt) =(mu_0in_0r')/2XX1/(in_0pir^2) V/R e^(-t/tau)`
`(mu_0r')/(2pir^2)xxV/R e^(-t/tau)`
`=((4pixx10^-7)xx(1//2))/(2PI(1)^2)xx4/((2xx10^3))e^-1`
`( :' t=10^-3s , tau=10^-3s)`
`=(2xx10^-10)/2.718=7.358xx10^-11T`
Discussion
39616.

Self inductance coefficient of a system can be increased by increasing the current through it b) decreasing the current through it c) inserting an iron core d) increasing the number of turns

Answer»

a, C only
c, d only
a, c, d
d only

Answer :B
Discussion
39617.

Degree of constant polynomial?

Answer»

1
2
4
0

Answer :D
Discussion
39618.

Rating of 12 V battery is 80 A, this means that if we join any conducting wire between two terminals of battery, we get 80 A electric current and internal resistance of battery = Omega.

Answer»

0
0.015
0.15
none of these

Solution :0.15
R= `(V)/(I) = (12)/(80) = 0.15 OMEGA`
Discussion
39619.

A seconds pendulum is mounted in a rocket. Its period of oscillation decreases when rocket is

Answer»

MOVING up with UNIFORM velocity
moving up with CONSTANT acceleration
moving DOWNWARD with uniform acceleration
nothing

Answer :B
Discussion
39620.

Wavelength of two notes in ai rare 80//195 m and 80//193 m. Each note produces five beats per second with a third note of a fixed frequency. Calculate the velocity of sound in air.

Answer»


ANSWER :D
Discussion
39621.

A negligibly small current is passed through a wire of length 15m and uniform cross-section 6.0xx10^(-7)m^2, and its resistance is measured to be 5.0 Omega. What is the resistivity of the material at the temperature of the experiment?

Answer»

SOLUTION :`2.0xx10^(-7) OMEGA m`
Discussion
39622.

A sonometer wire resonates with a given tuning fork forming standing waves with five antinodes between the two bridges when a mass of 9 kg is suspended from the wire. When the mass is replaced by M, the wire resonates with the same tuning fork forming three antinodes for the same position of bridges. The value of M is

Answer»

25 KG
5 kg
12.5 kg
`1/25` kg

ANSWER :A
Discussion
39623.

When a wheel with metal spokes 1.0 m long is rotated in a magnetic field of flux density 2xx10^(-4) T normal to the plane of the wheel, an emf of pixx10^(-2) V is induced between the rim and the axle. Find the rate of rotation of the wheel.

Answer»


ANSWER :50 RPS
Discussion
39624.

Tritium has a half-life of 12.5 y undergoing beta decay. What fraction of a sample of pure tritium with remain undecayed after 25 y?

Answer»

Solution :After 12.5 years, half the INITIAL sample will remain undecayed. In the NEXT 12.5 years ONE half of these NUCLEI undergoes decay. Therefore one-fourth of the initial sample of tritium will remain undecayed.
Discussion
39625.

About an electric field which of the following statements are not true ?

Answer»

If `E=0,V` must be zero
If `V=0,E` must be zero
If `E NE 0,V` cannot be zero
If `V ne 0,E` cannot be zero

Answer :A::B::C::D
Discussion
39626.

In double slit pattern (lambda = 6000 Å), the zero order and tenth order maxima fall at 12.34 mm and 14.73 mm from a particular reference point. If lambda is changed to 5000 Å, find the position of zero order and tenth order fringes, other set up being same :

Answer»

`6.2 mm`
`14.53 mm`
`7.2 mm`
94 mm

Solution :`beta = (14.73 - 12.34)/(10) = 0.239 mm, beta = (lambdaD)/(d)`
`THEREFORE 0.239 xx 10^(-3) = (6000 xx 10^(-10)D)/(d)`
or `(D)/(d) = 398.3`
When `lambda. = 5000 Å`
`beta. = (lambda.D)/(d) = 0.219 mm`.
The zero ORDER fringe will OCCUR at same position, at 12.34 mm. The 10th order at
`12.34 + 10 xx 0.219= 14.53 mm`.
Discussion
39627.

(A) : The sky waves are not used in the transmission of television signals. (R) : Sky waves are mechanical waves.

Answer»

Both 'A' and 'R' are TRUE and 'R' is the correct explanation of 'A'.
Both 'A' and 'R' are true and 'R' isnot the correct explanation of 'A'.
A' is true abd 'R' FALSE
A' is false and 'R' is false

ANSWER :C
Discussion
39628.

An oscilllator of frequency 680 Hz drives two speakers. The speakers are fixed on a vertical pole at a distance 3m from each other as shown in the fig. A person whose height is almost the same as that of the lower speaker walks towards the lower speaker in a direction perpendicular to the pole. Assuming that these is no reflection of sound from the ground and speed of sound is v = 340 m/s. At some instant, when the person is.at a distance 4m from the pole, the wave function (at the person.s location) that describes the waves coming from the lower speaker is y=A cos(kx - omegat),where A is the amplitude omega = 2piv with v = 680 Hz (given) and k=(2pi)/lambda wave function (at the person.s) location) that described waves coming from the upper speaker can be expressed as

Answer»

`y=Acos(KX - omegat +PI)`
`y = A cos(kx - omegat + pi//2)`
`y=A cos(kx - omegat + 2pi)`
`y=Acos(kx - omegat + (3PI)/2)`

Answer :C
Discussion
39629.

An oscilllator of frequency 680 Hz drives two speakers. The speakers are fixed on a vertical pole at a distance 3m from each other as shown in the fig. A person whose height is almost the same as that of the lower speaker walks towards the lower speaker in a direction perpendicular to the pole. Assuming that these is no reflection of sound from the ground and speed of sound is v = 340 m/s. As the person walks toward the pole, the total number of times that the person hears a minimum in sound intensity will be:

Answer»

2
8
4
6

Answer :D
Discussion
39630.

The resistance of the platinum wire of a platinum resistance thermometer at the ice point is 5 Omega and at steam point ins 5.23 Omega When the thermomenter is inserted in a hot bath, the resistance of the platinum wire is 5.795Omega. Calculate the temperature of the bath.

Answer»

SOLUTION :`R_(0) = 5 OMEGA , R_(100) = 5. 23 Omega and R_(t) = 5.795Omega`
Now, `t = ( R _(t) - R _(0))/( R _(100) - R _(0)) xx 100`
`= ( 5. 795 -5)/(5.23 -5) xx 10 0`
` = ( 0.795)/( 0.23) xx 10 0= 345.65^(@)C`
Discussion
39631.

The audio signal :

Answer»

Can be sent directly over the AIR for large distance
Cannot be sent directly over the air for large distance
Possess very HIGH frequency
None of the above

Answer :B
Discussion
39632.

Find integrals of given functions int x^(-3)(x + 1)dx

Answer»


Answer :`-(1)/(X)-(1)/(2X^(2))+C`
Discussion
39633.

A converging light beam incidents on diverging lens. After passing through lens, rays intersect at 15 cm behind the lens. If lens is kept away, then these rays intersect at 5 cm. Focal length of lens is ..

Answer»

`-10 cm`
20 cm
`-30` cm
5 cm

Solution :
ACCORDING to lens equation, `1/v-1/u=1/f`
u=-10 cm , v=15 cm ,f=(?)
`(1)/(15)-(1)/(10)=1/f`
`thereforef=-(150)/(3)`
`thereforef=-30` cm
Discussion
39634.

One - fourth length of a uniform rod is placed on a rough horizontal surface and it starts rotating about the edge as soon as we release it. The rod starts slipping on the edge when it has turned through an angle theta. If the coefficient of friction between rod and surface is mu, and it satisfies the relation x tan theta=4mu, then what is the value of x? ["Take "g=10m//s^(2)]

Answer»


ANSWER :13
Discussion
39635.

Two nuclei have mass numbers in the ratio 1:2. What is the ratio of their nuclear densities?

Answer»

SOLUTION :Densities of both NUCLEI are equal because NUCLEAR density is independent of the MASS number of a nuclide.
Discussion
39636.

A microscope is having objective of focal length 1 cm and eyepiece of focal length 6 cm. If tube length is 30 cm and image is formed at the least distance of distinct vision, what is the magnification produced by the microscope ? Take D=25 cm.

Answer»

6
150
25
125

Solution :`m = (L)/(f_(0))(1+(D)/(f_(E))) = (30)/(1)(1+(25)/(6)) = 155 ~~ 150`
Discussion
39637.

Two similar metal spheres are suspended by silk threads from the same point. When the spheres are given equal charges of 2 mu C the distance between them becomes 6cm. If length of each thread is 5 cm, the mass of each sphere is (g=10 m/s2)

Answer»

4 KG
3KG
`4/3 kg `
`1/3` kg

ANSWER :C
Discussion
39638.

Soap film of thickness 1 mu m appears bright when seen through reflected light of wavelength 700 nm. What should be the index of refraction of soap solution if it is somewhere between 1.2 and 1.3 ?

Answer»

Solution :Soap film appears bright by reflected light, hence condition of strong reflection is to be used and the same canbe written as follows :
`2 mu t = (2n + 1) lambda//2`
We can SEE in the above RELATION that `mu` and `n` are directly RELATED to each other. Hence for MINIMUM `mu` we can calculate minimum `n` and similarly for maximum `mu` we can calculate maximum n. And then in this range we need to find integer.
Maximum n :
`2nt = (2n+ 1) lambda/2`
`implies 2 xx 2 xx 1 xx 10^(-6) = (2n + 1)(700 xx 10^(-9))/(2)`
`implies 2n + 1 = (2 xx 1.3 xx 1 xx 10^(-6) xx 2)/(700 xx 10^(-9))`
`implies 2n + 1 = 7.43`
`implies 2n = 6.43`
`implies n = 3.21`
Integer between the ranges calculated above is just 3, so we can substitute it back to calculate the exact index of refraction.
`2mu t = (2n + 1) lambda//2`
`implies 2 xx mu xx 1 xx 10^(-6) = (2 xx 3 + 1) (700 xx 10^(-9))/(2)`
`implies mu = 7/(2 xx 10^(-6)) (700 xx 10^(-9))/(2)`
`implies mu = (7 xx 0.7)/(4)`
`implies mu = 1.225`.
Discussion
39639.

In n-type semiconductor when all donor states are filled, then the net charge density in the donor states becomes

Answer»

1
`GT1`
`LT1`but not zero
zero

Answer :B
Discussion
39640.

n_1 and n_2 are refractive indices of core and cladding of optical fibre respectively, then maximum acceptance angle theta = ......

Answer»

`SIN^(-1)((n_2)/(n_1))`
`sin^(-1)SQRT(n_1^2-n_2^2)`
`[TAN^(-1)(n_2)/(n_1)]`
`[tan^(-1)(n_1)/(n_2)]`

SOLUTION :`sin^(-1)sqrt(n_1^2-n_2^2)`
Discussion
39641.

A direct vision prism is made up of two prisms, one of flint glass and the other of crown glass. The flint glass prism has an angle of 10^(@) and mean index of refraction 1.650 . What must be the angle of the crown glass prism if its mean index of refraction is 1.5137? The diskpersive powers of flint and crown and glass are 0.0296 and 0.0175, respectively. Find also the angular separation of red and blue lights on emergence.

Answer»


ANSWER :`12^(@)39`',4'4''
Discussion
39642.

What is shunt? Obtain the formula for the shunt.

Answer»

Solution :1. LOW value RESISTOR connected across GALVANOMETER is known as shunt.

Equation of shunt :
2. Resistance of galvanometer be `R_(G)` and current flowing through it is `I_(G)`.
3. Resistance of shunt be `r_(s)` and current flowing through it is `(I-I_(G))`.
4. Apply Kirchhoff.s law in LOOP,
A-B-C-D-A,
`-I_(G)R_(G)+r_(s)(I-I_(G))=0`
`thereforer_(s)=(R_(G)I_(G))/((I-I_(G)))`
(I = current capacity of ammeter, `I_(G)` = current capacity of galvanometer)
Discussion
39643.

If the earth shrinks such that its mass does not change but radius decreases to one-quarter of its original value then one complete day will take

Answer»

96 h
48 h
6 h
1.5 h

Answer :D
Discussion
39644.

An ideal monoatomic gas of given mass is heated at constant pressure. In this process, the fraction of supplied heat energy used for the increase of the internal energy of the gas is

Answer»

`3/8`
`3/5`
`3/4`
`3/7`

SOLUTION :Using , `(DU)/(DQ) = C_(V)/C_(p) (dT)/(dT) = C_(v)/C_(p) = ((3/2 R))/((5/2 R)) = 3/5`
Discussion
39645.

A non - conducting disc of radius R is uniformly charged with surface charge density sigma. A disc of radius (R )/(2) is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be

Answer»

`(PI sigmaR)/(2epsilon_(0))`
`(sigmaR)/(2piepsilon_(0))`
`(sigmaR(pi-1))/(2PI epsilon_(0))`
`(sigmaR(pi-1))/(2epsilon_(0))`

ANSWER :C
Discussion
39646.

An amplifier has a voltage gain of 100 without feedback. A fraction of its output voltage is applied to input in such a way that the gain reduces to 50. Find feedback factor

Answer»

SOLUTION :`betaA=1`
Discussion
39647.

Derive an expression for resonant frequency of series circuit containing inductor, capacitor and resistor.

Answer»

SOLUTION :
Series LCR circuit is said to be in resonance when CURRENT through the circuit is maximum. In a series LCR circuit current amplitude is given by
`i_(m)=(V_(m))/(Z)`
`i_(m)=(V_(m))/(sqrt(R^(2)+(X_( C )-X_(L))^(2)))`
where `X_( C )=(1)/(omegaC)` and `X_(L)=omega_(L)`
If FREQUENCY is varied, at particular angular frequency `omega_(0)` the condition
`X_( C )=X_(L)` is achieved, this condition is called resonance, `(1)/(omega_(o)C)=omega_(0)L`
`:." "omega_(0)=(1)/(sqrt(LC))`
`2pi v_(o)=(1)/(sqrt(LC))""(because omega_(0)=2pi v_(0))`
`v_(0)=(1)/(2pi sqrt(LC))` is called resonant frequency
Discussion
39648.

Two identical balls one solid and other hollow are allowed to roll down an inclined plane, which one of them reached the base first?

Answer»

HOLLOW ball
Solid ball
Both REACH together
None reaches

Solution :For solid sphere `a=(5)/(7)gsintheta=0.7sintheta`
For hollow sphere `a=(3)/(5)gsintheta=0.6gsintheta`
Since acceleration of solid sphere is more than hollow sphere : solid sphere reaches the BOTTOM FIRST.
Discussion
39649.

The potential energy of a particle varies with distance x as U=(Ax^(1//2))/(x^(2)+B) where a and B are constants. The dimensional formula for AXB is :

Answer»

`M^(1)L^(7//2)T^(-2)`
`M^(1)L^(11//2)T^(-2)`
`M^(1)L^(5//2)T^(-2)`
`M^(1)L^(9//2)T^(-2)`

SOLUTION :Here `x^(2)` has the dimensions of `L^(2)`
`:.B=[L^(2)]`
Also `ML^(2)T^(-2)=(AL^(1/2))/(L^(2))`
or `A=ML^(7/2)T^(-2)`
`:.AxxB=ML^(11/2)T^(-2)`
HENCE correct choice is `(b)`.
Discussion
39650.

If L stands for coefficient of self inductance, R electric resistance and C for capacitance, then which of the following expression has the dimensions of time ?

Answer»

`L/sqrtR`
R/C
`SQRT(LC)`
`sqrt(RC)`

ANSWER :D
Discussion