Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 41601. |
A convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens. As in the lat problem, find the distance of A' below the optic axis of lens. |
|
Answer» |
|
| 41602. |
To explain his theory, Bohr used……… |
|
Answer» conservation of LINEAR momentum |
|
| 41603. |
A convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens. If A'B' is the final image formed, A' corresponding to A and B' corresponding to B, find the distance of B' below optics axis of lens. |
|
Answer» 0.3 m |
|
| 41604. |
A real image of an object is formed on a screen at a distance of 50 cm from a convex lens . A person holdshis spectacles in between the screen and theconvex lens at a distance of 5 cm from the lens . If the screen is moved 15 cmtowards the lens again a real image is formed , what is the focal length of the spectacles ? what is the nature of defect of his vision ? |
|
Answer» |
|
| 41605. |
A circuit containing resistance R_(1), inductance L_(1) and capacitance C_(1) connected in series resonates at the same frequency 'n' as a second combination of R_(2), L_(2)" and "C_(2). If the two are connected in series. Then the circuit will resonates at |
|
Answer» n |
|
| 41606. |
(A) : In electric circuits, wires carrying currents in opposite directions are often twisted together. (R) : If the wire are not twisted together, the combination of the wires forms a current loop. The magnetic field generated by the loop might affect adjacent circuits or components. |
|
Answer» Both 'A' and 'R' are TRUE and 'R' is the CORRECT explanation of 'A'. |
|
| 41607. |
Light of frequency 7.21xx10^(14) Hz is incident on a metal surface .Electrons with a maximum speed of 6.0xx10^(5)m//s are ejected from the surface .What is the threshold frequency for photoemission of electrons? |
|
Answer» Solution :Here frequency v`=7.21xx10^(14)` Hz `v_(max)=6.0xx10^(5)m//s` `V_(0)=?h=6.63xx10^(-34)Js` `m=9.1xx10^(-31)Js` `m=9.1xx10^(-31)KG` `implies`From Einstien.s EQUATION of photoelectric effect. `K_(max)=hv-phi_(0)` `therefore (1)/(2)mv^(2)max=hv-hv_(0)` `thereforehv_(0)=hv-(1)/(2)mv^_(max)(2)` `therefore v_(0)=v-(mv_(max)^(2))/(2h)` `=7.21xx10^(14)-(9.1xx10^(-31)xx36xx10^(10))/(2xx6.63xx10^(-34))` `=7.21xx10^(14)-2.47xx10^(14)` `therefore v_(0)4.74xx10^(14) Hz` |
|
| 41608. |
I a magnetis divided in to 2n parts by cutting along lines parallel to length then polestrength of each part will be |
|
Answer» same |
|
| 41609. |
The maximum intensity of fringes in Young's double-slit experiment is I. if one of the slit is closed, the intensity at that place becomes I_(0). Which of the following relation is true ? |
|
Answer» `I=I_(0)` If one slit is closed then maximum intensity `I_(0)=I_(1)IMPLIES I=4I_(0)`. |
|
| 41610. |
A radioactive isotope has a half-life of T years.How long will it take the activity to reduce to , |
|
Answer» 4.5 T and 7.5 T |
|
| 41611. |
Two long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity sigma and a constant potential difference V is maintained between them by a battery. Then the current per unit length of the cylinder flowing from one cylinder to the other is |
|
Answer» `(4pisigma)/(LN(b//a))V ` cylinder. And `V = int_ (a)^(b) Edl = lambda/(2piepsilon_0) In (b/a)` Now, `I = int vec(J).d vec(A) = sigma int vec(E ) * d vec (A)` ` = sigma int (lambda/(2piepsilon_0r)) 2pir dr ` Current per unit LENGTH will be `I = (sigmalambda)/(epsilon_0)` From Eq. (i), we get `I = (2sigmapiepsilon_0)/(epsilon_0In (b//a)) v = (2pi sigma)/(In(b//a)) v` Alternatively, `I = V/R or R = int_(x=a)^(b) (i/sigma)(dx)/(2pix 1) = 1/(2pir) In (b/a)` `:.I = (2pisigmaV)/(In (b//a))` . |
|
| 41612. |
A cylindrical vessel with water is rotated about its vertical axis with a constant angular velocity omega. Find: (a) the shape of the free surface of the water, (b) the water pressure distribution over the bottom of the vessel along its radius provided the pressure at the central point is equal to p_0. |
|
Answer» Solution :The Euler's equation is `rho(dvecv)/(dt)=vecf-vecnablap` in the space fixed frame where `vecf=-rhogveck` downward. We assume incompressible fluid so `rho` is constant. Then `vecf=-vecnabla(rhogz)` where Z is the height vertically upwards from some fixed origin. We go to rotating frame where the equation becomes `rho(dvecv)/(dt)=-vecnabla(p+rhogz)+rhoomega^2+2rho(overset(rarr')vxxvecomega)` the additional terms on the right are the well known coriolis and centrifugal FORCES. In the frame rotating with the liquid `overset(rarr')v=0` so `vecnabla(p+rhogz-1/2rohomega^2r^2)=0` or `p+rhogz-1/2rhoomega^2r^2=consta nt` On the free surface `p=const ant`, thus `z=(omega^2)/(2g)r^2+const ant` If we choose the origin at point `r=0` (i.e. the axis) of the free surface then "constant" =0 and `z=(omega^2)/(2g)r^2` (The PARABOLOID of REVOLUTION) At the bottom `z=const ant` So `p=1/2rhoomega^2r^2+const ant` If `p=p_0` on the axis at the bottom, then `p=p_0+1/2rhoomega^2r^2`. |
|
| 41613. |
In a P-type semiconductor, the dopant material used is |
|
Answer» arsenic |
|
| 41614. |
Magnetic flux linked with one coil changes with time t is phi=xt^2 . If emf induced at t=3s is 9 V then value of x = ...... |
|
Answer» 0.66 `"WB s"^(-2)` `therefore (dphi)/(dt)=2xt` INDUCED emf, `epsilon=-(dphi)/(dt)` `epsilon=-2xt` `therefore x=-epsilon/(2T)=-9/(2xx3)=-1.5 "Wb s"^(-2)` |
|
| 41615. |
Let u_(a) and u_(d) represent the energy density (energy per unit volume) in air and in a dielectric respectively, for the same field in both. Let K= dielectric constant. Then |
|
Answer» `u_(a)=u_(d)` |
|
| 41616. |
A short magnet produces a deflection of 45^(@) along the east of deflection magnetometer, at a certain distance. When kept at the same distance in the south, the deflection will be : |
| Answer» Answer :A | |
| 41617. |
When two capacitors are connected in series and connected across 4kV line, the energy stored in the system is 8 J. the same capacitors, if connected in parallel across the same line, the energy stored in 36 J. find the individual capacitances. |
|
Answer» SOLUTION :`E=(1)/(2)CV^(2)` finding `C_(1)+C_(2)=4.5xx10^(-6)F` finding `C_(1)+C_(2)=4.5xx10^(-12)` Final answer `C_(1)3muF` and `C_(2)=1.5muF` Detailed `E_(S)=(1)/(2)C_(S)V^(2)=(1)/(2)[(C_(1)C_(2))/(C_(1)+C_(2))]V^(2)` . . (1) `E_(p)=(1)/(2)C_(p)V^(2)=(1)/(2)[C_(1)+C_(2)]V^(2)`. . (2) `8=(1)/(2)[(C_(1)C_(2))/(C_(1)+C_(2))]xx(4xx10^(3))^(2)`. . (4) `36=(1)/(2)[C_(1)+C_(2)]xx(4xx10^(3))`. . (5) on SOLVING equation (4) and (5) we get `C_(1)=3muF,C_(2)=1.5muF`. |
|
| 41618. |
What is shown by Thomson's experiments of electric discharge through gases ? And explain the plum pudding model. |
|
Answer» Solution :These experiments SHOWED the atoms of various elements contain negatively charged constituents (electrons). They are identical for all atoms. All atoms are electrically neutral even though they have negatively charged constituents. Therefore, an atom must also contain some POSITIVE charge to neutralise the negative charge of the electrons. To understand this, Thomson understood the ATOMIC model called PLUM Pudding Model of the atom. According to this model, the positive charge of the atom is uniformly distributed throughout the volume of the atom. In this model the negatively charged electrons are embended in it like SEEDS in a watermelon, This called plum pudding model of the atom. |
|
| 41619. |
An achromatic objective of focal length 1.5mis to be constructed with a crown glass convex lens (mu=1.51, omega=0.21) and a flint glass concave lens (mu=1.65, omega=0.45) One face of the concave lense is in complete contact withthe convex lens and the other face is plane. Calculate the curvatures of the surfaces. |
|
Answer» |
|
| 41620. |
A spherical surface is split into two parts, S_(1) and S_(2), by a circular loop. The sphere is placed near a bar magnet, as shown in the following figure. Through which of the two parts is the magnitude of the magnetic flux larger? |
|
Answer» `S_(1)` |
|
| 41621. |
An inductor of inductance L and resistor R are joined together in series and connected by a source of frequency omega. The power dissipated in the circuit is |
|
Answer» `(V)/(R^2+ OMEGA^2 L^2)` ` P=V _(" RMS")I_("rms") cos phi,cosphi= (R )/( Z ) = V(V )/(Z ), (R )/(Z)= (V^2 R)/(sqrt(R^2 =( Omega L)^2)))` |
|
| 41622. |
Assuming that about 20 MeV of energy in released per fusion in the reaction ""_(1)H^(2)+""_(1)H^(3) to ""_(0)n^(1)+ ""_(2)He^(4). then the mass of ""_(1)H^(4) consumes per day in a bowiem reactor of puwwer Imawat will styroximately be: |
|
Answer» 0.001gm `=10^(6) XX 24 xx 60 xx 60 J//day` Energy/fusion `=20 xx 10^(6)eV` `=20 xx 10^(6) xx 1.6 xx 10^(-19)J` In each fusion, MASS of `""_(1)H^(2)` used =2 a.m.u. `=2 xx 1.6 xx 10^(-27)kg ..........(1)` Number of fusion/day `=(10^(6) xx 24 xx 60 xx 60)/(20 xx 10^(6) xx 1.6 xx 10^(-19))` Mass consumed//day of `""_(1)H^(2)` `=(10^(6) xx 24 xx 60 xx 60)/(20 xx 10^(6) xx 1.6 xx 10^(-19)) xx 2 xx 1.6 xx 10^(-27)kg` `approx 10^(-4)kg=0.1gm` |
|
| 41623. |
In L-C oscillator circuit inductor ………. |
|
Answer» having high RESISTANCE |
|
| 41624. |
Domain and range of greatest integer Functions are respectively |
|
Answer» R,I |
|
| 41625. |
Given below are some functions of x and t to represent the displacement the displacement ( transverseor longitudinal ) of an elasticwave. State which of these represent (i) atravelling wave, (ii) a stationary wave or ( iii) none at all : (a)y = 2cos ( 3x ) sin ( 10 t ) (b)y= 2 sqrt(x-vt) (c ) y =3 sin ( 5x - 0.5 t ) + 4 cos ( 5x- 0.5 t ) (d)y cos x sin t+ cos 2x sin 2t |
|
Answer» Solution :(a) It represents a stationary wave as harmonicfunctions of x & t are contained separately in the equation . (b) It cannot represent any type of wave. (c ) It represents a PROGRESSIVE `//` travelling harmonic wave. (d ) This equation is SUM of two FUNCTIONS each representing a stationary wave. Therefore it represents SUPERPOSITION of two stationary waves. |
|
| 41626. |
Magnetic flux of 5 microweber is linked with a coil, when a current of 1mA flows through it. What is the self-inductance of the coil? |
| Answer» Solution :`5 xx 10^(-3)H` | |
| 41627. |
When a dielectric slab of thickness 6 cm is introduced between the plates of parallel plate condenser, it is found that the distance between the plates has to be increased by 4 cm to restore to capacityoriginal value. The dielectric constant of the slab is |
|
Answer» `1.5` |
|
| 41628. |
Figure shows a cylindrical vessel of height 90 cm filled upto the brim. There are four holes in the vessel as shows in figure . The liquid falling at maximum horizontaldistancefromthe vesselwould come from |
|
Answer» hole 1 ` t = sqrt((2H)/g)` ` " RANGE "= vt = 2 sqrt(h(H-h))` `R_(1) = 2 xx sqrt(20 xx (90 - 20)) = 20 sqrt(14) cm , ""R_(2) = 2 xx sqrt(30 xx (90 - 30)) = 20 sqrt(18)` cm ` R_(3) = 2 xx sqrt(40 xx (90 - 40)) = 20 sqrt(20) cm "" R_(4) = 2 xx sqrt(50 xx (90 - 50 )) = 20 sqrt(20) ` cm |
|
| 41629. |
When frequencies f_(1) and f_(2) are incident on two indentical photo sensitive surfaes ,maximum velocities of photo-electrons of mass m are v_(1) and v_(2) hence…… |
|
Answer» `v_(1)^(2)-v_(2)^(2)=(2h)/(m)(f_(1)-f_(2))` `(1)/(2)mv_(max)^(2)=HF-phi` `therefore hf=(1)/(2)mv_(max)^(2)+phi` `therefore hf_(1)=(1)/(2)mv_(1)^(2)+phi [because v_(max)=v_(1)]` and `hf_(2)=(1)/(2)mv_(2)^(2)+phi[because v_(max)=v_(2)]` `therefore H(f_(1)-f_(2))=(1)/(2)m(v_(1)^(2)-v_(2)^(2))` `therefore (2h)/(m)(f_(1)-f_(2))=v_(1)^(2)therefore v_(1)^(2)-v_(2)^(2)=(2h)/(m)=(2h)/(m)(f_(1)-f_(2))` |
|
| 41630. |
Do the same exercise as above with the replacement of the earlier transformer by a 40,000-220V step-down transformer (Neglect, as before, leakage losses though this may not be a good assumption any longer because of the very high voltage transmission involved). Hence, explain why high volage transmission is preferred ? |
|
Answer» Solution :Given primary VOLTAGE `V_(P)=40,000 V` Let the current in primary is `I_(P)` `therefore V_(P)I_(P)=P` `800xx1000=40000 xx I_(P)` `I_(P)=20A` (a) Line power loss `= (I_(P))^(2)xxR` `= (20)^(2)xx2xx0.5xx15` `= 6000W = 6KW` (B) Power SUPPLY by plant `= 800+6=806KW` Voltage drop of line `= I_(P).R` `= 20xx2xx0.5xx15` = 300 V Voltage for transmission `= 40000+300=40300V` Power loss at higher voltage `= (6)/(800)xx100=0.74%` Power loss at lower voltage `= (600)/(1400)xx100=42.8%` Hence, the power loss is minimum at higher voltage. So, the high voltage transmission is preferred. |
|
| 41631. |
Two plane mirrors are inclined at an angle of 60^@ with each other. An incident ray hits one of the mirror at an angle of 80^@ with the normal. Its angle of deviation after two reflections is |
| Answer» ANSWER :A | |
| 41632. |
A certain particle has a half life of 60 seconds. The fraction of the particles that will decay at the end of 10 seconds is |
|
Answer» `2^(1//6)` |
|
| 41633. |
A body initially at rest is moving with uniform acceleration 'a'. It's velocity after n seconds is v. The displacement of the body in last 2 seconds is: |
|
Answer» `(2v(N-1))/(n)` `s=(a)/(2)[n^(2)-n^(2)-4+4n]` =2a[n-1] Also `a=("VELOCITY")/("time")=(v)/(n)` `:. S=(2v(n-1))/(n)` |
|
| 41634. |
In the following nuclear reaction, identify the particle X: n → p+e^(-)+X. |
| Answer» SOLUTION :ANTINEUTRINO or `OVERLINE(V)`. | |
| 41635. |
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12 m//s^2. Find the displacement of the block during the first 0.2 s after the start. Take g = 10 m//s^2 |
| Answer» Answer :C | |
| 41636. |
Hard X-rays for the study of fractures in bones should have a minimum wavelength of 10^(-11)m. The accelerating voltage for electron in X-ray machine should be ..... |
|
Answer» `lt 124.2kV` `:.V=(1.24xx10^(-6))/(10^(-11))=124.2kV` The ACCELERATING voltage for electrons in X-ray MACHINE should be greater than |
|
| 41638. |
The maximum kinetic energy of the photoelectrons depends only on : |
|
Answer» potential |
|
| 41639. |
What is Rectification? Describe with a circuit diagram the working of a p-n junction diode as half wave rectifier with input and output waveforms. |
Answer» Solution :The process of converting ac into dc is called rectification   The diode D in series with a load resistor `R_(L)` is connected to the secondary of the transformer. The ac voltage to be rectified is applied to the primary of the transformer. The secondary of a transformer supplies the DESIRED ac voltage across terminals A and B. The output dc voltage is taken across the load `R_(L)`. WORKING: During the POSITIVE half cycle of input ac voltage, the end A becomes positive with respect to the end B. As a result the diode becomes forward biased and conducts the current. The current flows in the direction `ADR_(L)BA`. During the negative half cycle of input ac voltage, the end A becomes negative with respect to teh end B. As a result the diode becomes reverse biased and does not conducts the current. Thus the current flows through the diode during positive half cycle only. The current flows through the load `R_(L)` ALWAYS in the same direction. HENCE dc output is obtained. |
|
| 41640. |
Fig. 9.12 shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0 cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0 cm. What is the refractive index of the liquid ? |
|
Answer» SOLUTION :From the first measurement we get the value of focal length/of the COMBINATION of equiconvex lens and a planoconcave LIQUID lens i.e f = 45.0 CM. From the second measurement we find the focal length fx of the equiconvex lens i.e `f_(1) = 30.0 cm` If `f/2`be the focal length of planoconcave liquid lens, then `1/f =1/f_(1) + 1/f_(2)` or `1/f_(2) =1/f -1/f_(1) =1/45 -1/30 =-1/90 rArr f_(2) =-90 cm` Using lens maker.s formula for equiconvex lens, we get `1/f_(2) =(n_(1)-1) [1/(-R) -1/infty]` `1/(-90) = (n_(1)-1) [1/(-30) -1/infty] =-(n_(1)-1)/30` or `(n_(1)-1) = 30/90 = 0.33 rArr n_(1) = 1.33` |
|
| 41641. |
In a building there are 15 bulbs of 45 W, 15 bulbs of 100 W, 15 bulbs of 10 W and 2 heaters of 1 kW. The voltage of electric main is 220 V. The minimum fuse capacity (rated value ) of the building will be approximately . |
|
Answer» Solution :20A Total POWER, `15 xx 45 + 100 xx 15 + 10 xx 15 + 1000 xx 2 ` `P = 675 + 1500 + 150 + 2000` `therefore P = 4325` W Now, `VI = 4325` `therefore I= (4325)/(V) = (4325)/(220)` `therefore I = 19.659 A "" therefore I = 20 `A |
|
| 41642. |
A ball falls freely from a height of 180 m on to a hard horizontal floor and repectedly bounces . If the coefficient of restitution is 0.5 the average speed and aberage velocity of the ball before it ceases to rebound are respectively( acceleration due to gravity = 10 "ms"^(-2)) |
|
Answer» `10 MS^(-1), 10 ms^(-1)` 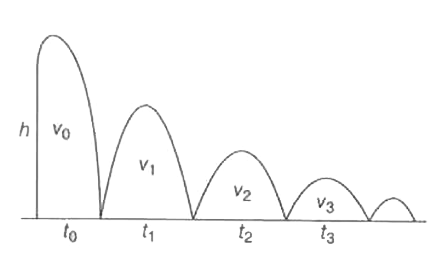 When ball dropped from height h then time taken to reach the ground `t_(0)sqrt((2h)/(g))` and speed `v_(0)= sqrt(2gh)` After first COLLISION its speed will become `v_(1)=ev_(0)=esqrt(2gh)` where e= coefficient of restitution . Now the ball will go up and will take time `t_(1)` when it STOPS `nu = mu + at ` `o= v_(1)-"gt"_(1)` `t_(1)= (v_(1))/(g)` It will coem down and take same time `t_(1)` before second collision.So time taken between first and second collision is `2t_(1)` . Similarly time taken between second and third collision will be `2t_(3)= (2v_(2))/(g)` Total time before it ceaser to REBOUND `T= t_(0)+2t_(1)+2t_(2)+ .........` ` T = t_(0)+ (2v_(1))/(g)+ (2v_(2))/(g) + ..........` `T= t_(0)+ (2ev_(0))/(g)+(2e^(2)v_(0))/(g)+...........` {as`v_(2)=ev_(1)=e^(2)v_(0)}` `T=sqrt((2h)/(g))[I+2e(1+e+e^(2)+e^(3)+cdots)]` `{as v_(0)= sqrt(sqrt(2h)/(g))}` It forms a GP, `T=sqrt((2h)/(g))[1+2e((1)/(1-e))]` `T=sqrt((2h)/(g))((1+e)/(1-e))` T= `6xx3 = 18 s` Calculation of distance in ENTIRE motion intitial height `h_(0)` = h After first collision = `h_(1) ` As ` e = (v)/(u)= =sqrt((2gh_(1))/(2gh_90))=sqrt(h_(1)/(h))` `h_(1)=e^(2)h` similarly `h_(2)= e^(2)(e^(2)h)` `h_(2)= e^(4)h` Total distance , `H=h_(0)+2h_(1)+2h_(2)+ .........` `H= h+2e^(2)h+2e^(4)h+ ............. ` `H = h[I+2e^(2)(1+e^(2)+e^(4)+ ...........)]` ` H =h [1+2e^(2)((1)/(1-e^(2)))]` `H=h((1+e^(2))/(1-e^(2)))` `H= 180 ((1+(1)/(4))/(1-(1)/(4)))e = 0.5 = (1)/(2)` `H= 180 xx(5)/(3)` H= 300 m Average speed v = `("Total distance" )/("Time")` `v=(300)/(18) = (50)/(3) `m/s Average velocity `v = ("Total displacement")/("Time")` `v=(180)/(18) = 10 ` m/s |
|
| 41643. |
Two coherent monochromatic light beams of of intensities I and 4I are superposed. The maximum and minimum intensities in the resulting beam are |
|
Answer» 5I and I `THEREFORE I_(max)=I+4I+2sqrt(I*4I)(1)=9I and I_("min")=I+4I+2sqrt(I*4I)(-1)=I`. |
|
| 41644. |
A swimming pool is filled with water up to its brim. A swimmer observes a source of light just over the edge of the pool looking from a depth of 2 m in water and at a distance of 1.5 m from the vertical wall of the pool. The source of the light is placed at a height of 3 m from the ground and at a distance of 4 m from the edge of the pool. Find the refractive indexof water in the swimming pool. |
|
Answer» |
|
| 41645. |
The nucleus ""_(10)^(23)Ne decays by beta^(-) emission. Write down the beta-decay equation and determine the maximum kinetic energy of the electrons emitted. Given that: m (""_(10)^(23) Ne) = 22.994466 u m (""_(11)^(23)Na) = 22.989770 u. |
|
Answer» SOLUTION :The equation is `""_(10)^(23)Ne to ""_(11)^(23)Na + beta + BARUPSILON +Q` `Q = [m_n(""_(10)^(23)Ne) - m_(N) ""_11^23Na - m_e]c^2` (Neglect the rest mass of `barupsilon)` `= {{m_n ""_(10^(23)Ne + 10 m_e} - {m_n(""_11^23Na) + 11m_e}]c^2` `= [m ""_(10)^(23)Ne - m ""_(11)^(23)Na]c^2` `=[22.994466 - 22.989770]931` `= 4.374 MeV`. |
|
| 41646. |
The same capacitors are connected in series. Find the resultant capacitance. |
Answer» Solution :When the CAPACITORS are connected in series (Fig. 24.10), their charges are redistributed so that the charges of all the capacitors are  equal. To make sure that this is so, consider using Fig. 24.10, what will happen if the system is discharged by shortcircuiting the points at potentials`varphi_(1) and varphi_(2)`. We have `varphi_(1)-varphi.=q//C_(1), varphi.-varphi_(2)=q//C_(2)` For the system as a whole, Q C g/C. ADDING the two former EQUATIONS and comparing the result with the THIRD, we obtain the formula sought. |
|
| 41647. |
The coefficient of thermal conductivity depends upon : |
|
Answer» temperature difference between two sides Thus correct CHOICE is (c ). |
|
| 41648. |
A constant potential difference is applied across a resistance. Consider variation of resistance with temperature. Which graph represents best the variation of power produced in resistance versus resistance? |
|
Answer»
|
|
| 41649. |
Name the physical quantity whose SI unit is JC. Is it a scalar or vector quantity ? |
| Answer» SOLUTION :ELECTRIC POTENTIAL, which is a SCALAR QUANTITY. | |
| 41650. |
When the applied potential difference across a circuit element is increased linearly with time as shown in the second figure, the current in the circuit remains constant with time as shown in the first figure. At t = 4 s the lead wire connecting the element to the source breaks. What will be the voltage across the element after t = 4 s ? Can you identify the element? |
|
Answer» |
|



