Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 41951. |
Describe schematically the equipotential surfaces corresponding to a. a constant electric field in the z-direction. b. a field that uniformly increases in magnitude but remains in a constant (say,z) direction. c. a single positive charge at the origin, and d. a uniform grid consisting of long equally spaced parallel charged wires in a plane. |
Answer» Solution :a. EQUALLY spaced x-y planes. 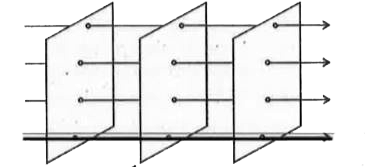 B. x-y planes getting closer and closer along the z-direction. 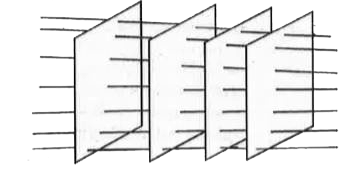 c. Concentric SPHERICAL surfaces gradually increasing in spacing. 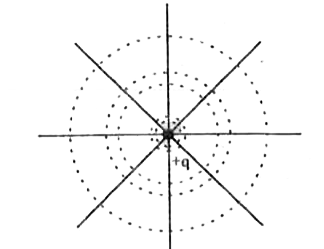 d. A periodically varying shape near the GRID which gradually reaches the shape of the planes parallel to the grid at far distances. 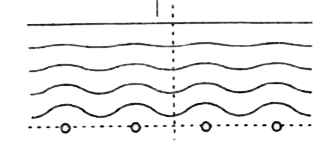
|
|
| 41952. |
गुणोत्तर श्रेढ़ी 1+1/2+1/4.. . के n पदों का योग है |
|
Answer» `1/2^n` |
|
| 41953. |
Calculate the critical angle inside a denser medium if it's RI is 2/sqrt3 ? |
| Answer» SOLUTION :`MU`=1/SIN C or sin c=`1/mu`=`sqrt3/2`[ `mu`=`2/sqrt3`] or,sin c = sin`60^@D` or C= `60^D@` | |
| 41954. |
In the given table, Columns I and II given statements regarding different types of motion of particle along straight line and Column III shows figures depicting the motion. (1) Which combination of statements is characteristic of oscillatory motion ? |
|
Answer» (I) (II) (J) |
|
| 41955. |
write equation the magnetic field due to current carrying loop as magnetic dipole on its axial point. |
|
Answer» Solution :1. The magnetic field on the AXIS of a circular loop of a radius R, carrying a steady current I, at x distance from centre is given by `B=(mu_(0)IR^(2))/(2(x^(2)+R^(2))^(3/2))""...(1)` 2. And its DIRECTION is along the axis and the right hand thumb rule. Here, x is the distance along the axis from the centre of the loop. 3. For `xgtgtR`, we MAY neglect `R^(2)` term in the denominator. Thus, `B=(mu_(0)IR^(2))/(2x^(2))""...(2)` 4. Multiply right SIDE of EQUATION (2) with `pi` in denominator and numerator, `thereforeB=(mu_(0)I(piR^(2)))/(2pix^(3))` Area of coil A = `piR^(2)` `thereforeB=(mu_(0)IA)/(2pix^(3))` Here, IA = magnetic dipole moment = m `B=(mu_(0)m)/(2pix^(3))` `thereforeB=(2mu_(0)m)/(4pix^(3))` and In vector form, `thereforevecB=mu_(0)/(4pi)((2vecm)/x^(3))` which is formula for magnetic field on point of axis of coil. |
|
| 41956. |
The electric field at (30,30) cm due to a charge of - 8 nC at the origin in NC^(-1) is |
|
Answer» `-400 (hat(i) - hat (J))` |
|
| 41957. |
A mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is |
|
Answer» `2pi SQRT((m)/(k))` `t_(1) = pi sqrt((m)/(2k))` when mass moves upwards only Upper spring is effective `t_(2) = pi sqrt((m)/(k))` `:.` Time period `T = t_(1) + t_(2)` `T = pi sqrt((m)/(2k)) + pi sqrt((m)/(k))` 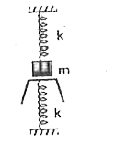
|
|
| 41958. |
A diode detector is used to detect an amplitude modulated wave of 60% modulation by using a condenser of capacity 20 picofarad in parallel with a load resistance 100 kilo ohm. Find the maximum modulated frequency which could be detected by |
|
Answer» 10.62 kHz |
|
| 41959. |
As a car rolls along pavement, electrons move from the pavement first onto the tires and then onto the car body. The car stores this excess charge and the associated electric potential energy as if the car body were onc plate of a capacitor and the pavement were the olher plate (Fig. 27-35a). When the car stops, it discharges its excess charge and energy through the tires, just as a capacitor can discharge through a resistor. If a conducting object comes within a few centimeters of the car before the car is discharged, the remaining energy can be suddenly transferred to a spark between the car and the object. Suppose the conducting object is a fuel dispenser. The spark will not ignite the fuel and cause a fire if the spark energy is less than the critical Value U_("fire")=50 mJ. When the car of Fig. 27-35a stops at time t=0, the car ground potential difference is V_(0)=30kV. The car-ground capacitance is C= 500 pF, and the resistance of each tire is R_("tire")= 100G Omega. How much time does the car take to discharge through the tires to drop below the critical value U_("fire")? |
|
Answer» SOLUTION :(1) At any time t, a capacitor.s stored electric potential energy U is related to its stored charge d according to Eq. 25-21 `(U=q^(2)//2C)` While a capacitor is discharging, the charge decreases with time according to Eq. 27-49 `q=q_(0) e^(-1//RC)` Calculations. We can TREAT the times as resistors that are connected to one another at their tops via the car body and at their bottoms via the pavement. Figure 27-35b shows how the four resisters are connected in parallel across the car.s capacitance and Fig. 27-35c shows  Figure 27-35 (a) A charged car and the pavement acts like a capacitor that can discharge through the tires (b) The effective circuit of the car-pavement capacitor, with four tire resistances `R_("tire")` connected in parallel. (c) The equivalent resistance R of the tires. (d) The electric potential energy U in the car-pavement capacitor decreases during discharge. their equivalent resistance R. From Eq. 27-24, R is given by `1/R=(1)/(R_("tire"))+(1)/(R_("tire"))+(1)/(R_("tire"))+(1)/(R_("tire"))` `or R=(R_("tire"))/(4)=(100 xx 10^(9) Omega)/(4)=25 xx 10^(9) Omega`. When the car stops, it discharges its excess charge and energy through R. We now use our two Key Ideas to analyze the discharge Substituting Eq. 27-49 into Eq. 25-21 gives `U=q^(2)/(2C) =(q_(0) e^(-t//RC^(2)))/(2C)=q_(0)^(2)/(2C) e^(-2T//RC)` From Eq. 25-1 (q= CV), we can relate the initial charge `q_(0)` on the car to the given initial potential difference `V_(0):q_(0)= CV_(0)`. Substituting this equation into Eq. 27-55 brings us to `U=((CV_(0))^(2))/(2C) e^(-2t//RC)=(CV_(0)^(2))/(2) e^(-2t//RC)` `or e^(-2t//RC)=(2U)/(CV_(0)^(2))`. Taking the natural logarithms of both sides, we obtain `-(2t)/(RC)=ln (2U)/(CV_(0)^(2))`. or `t=-(RC)/(2) ln (2U)/(CV_(0)^(2))` Substituting the given data, we find that the time the car takes to discharge to the energy level `U_("fire")="50 mJ is"` `t=((25 xx 10^(9) Omega) (500 xx 10^(-12)F))/(2)` `xx ln (2(50 xx 10^(-3)J))/((500 xx 10^(-12) F) (30 xx 10^(3) V)^(2))` =9.4 s Fire or no fire: This car requires at least 9.4 s before fuel can be brought safely near it. A pit crew cannot WAIT that long. So the tires include some type of conducting material (such as carbon black) to lower the tire resistance and thus increase the discharge rate, Figure 27-35d shows the stored energy U versus time t for tire resistances of `R= 100 G Omega` (our value) and `R=10 G Omega.` Note how much more rapidly a car discharges to level `U_("fire")` with the lower R value. |
|
| 41960. |
(a) What is the gravitational potential energy of the two-particle system in Problem 22? If you triple the separation between the particles, how much work is done (b) by the gravitational force between the particles and (c) by you? |
| Answer» Solution :(a) `-7.6xx 10^(-11)J,` (b) `-5.1 xx 10^(-11) J,` (C ) `5.1 xx 10^(-11) J` | |
| 41961. |
The mass of the astronauts in a space station cannot be checked with the scales used on the Earth. Instead we use a spring balance, which oscillates when a mass is suspended from it. Imagine a seat of a mass of 20 kg, which, oscillates with a frequency of 2 Hz. After the astronaut sits in the seat the frequency decreases to 1 Hz. How much is the mass of the astronaut ? |
|
Answer» 40kg `implies m_(2)=80kg,m_(a)=60kg` . |
|
| 41962. |
Suppose that the lower half of the concave mirror’s reflecting surface in Fig. 9.5 is covered with an opaque (non-reflective) material. What effect will this have on the image of an object placed in front of the mirror? |
| Answer» Solution :You may think that the image will now show only half of the object, but taking the LAWS of reflection to be TRUE for all POINTS of the remaining part of the MIRROR, the image will be that of the whole object. However, as the area of the REFLECTING surface has been reduced, the intensity of the image will be low (in this case, half). | |
| 41963. |
According to the kinetic theory of gases, the root mean velocity of gas molecules is directly proportional to |
| Answer» SOLUTION :`v_(rms)=sqrt((3)/(2)KT)therefore v_(rms)=sqrt(T)` | |
| 41964. |
Current of 50/pi Hz frequency is passing | through an A.C. circuit having series combination of resistance R = 100Omega and inductor L = sqrt3H. The phase difference between the voltage and current is ….. |
|
Answer» `30^@` `=(100xxsqrt3)/100` `f=50/pi rArr 2pif =100` `therefore (omega)` = 100 rad/sec `=sqrt3` `= phi=60^@` |
|
| 41965. |
A galvanometer of resistance 20Omega gives a current of 10mA. To convert into a 50Vvoltmeter ,the resistance connected to it is : |
|
Answer» `4980Omega`RESISTANCE in SERIES |
|
| 41966. |
What is the probability of cold electron emission from tungsten, if the field strength at the point is 5xx10^(10)V//m? |
|
Answer» |
|
| 41967. |
What is meant by 1 eV |
| Answer» SOLUTION :1 ev is the energy acquired by an electron, when it is ACCELERATED through a potential DIFFERENCE of one VOLT. | |
| 41968. |
What is the de-Broglie wavelength associated with (a) an electrin moving with a speed of 5.4xx10^(6)m//s and (b) a ball of mass 150 g travelling at 30.0 m/s? |
|
Answer» 1.47 nm |
|
| 41969. |
In question 55, which region or regions of the figure could the electric field be zero? |
|
Answer» Near A |
|
| 41970. |
Two nuclei have their mass numbers in the ratio of 1:3. The ratio of their nuclear densities would be |
|
Answer» `(3)^(1//3):1` Their RADII will be in the ratio `R_0A_1^(1//3) : R_0A_2^(1//3)=1:3^(1//3)` DENSITY,`rho=A/(4/3piR^3)` `THEREFORE rho_(A_1):rho_(A_2)=1/(4/3 piR_0^3. 1^3):3/(4/3piR_0^3(3^(1//3))^3)=1:1` Their nuclear densities will be the same . |
|
| 41971. |
Define mutual inductance. |
|
Answer» SOLUTION :(i) Mutual inductance of TWO coils is the MAGNETIC flux linked with the secondary COIL when a unit current flows through the primary coil, i.e., `phi_2=MI_1" or" M=phi_2/I_1` |
|
| 41972. |
In the above problem find the magnetic field (a) near the ends of the solenoid. (b) outside the solenoid near its centre |
|
Answer» SOLUTION :(a) `1.05 xx 10^(-2)T` (B) zero |
|
| 41973. |
The radiation emitted when an electron jumps from n=3 to n = 2 orbit in a hydrogen atom, falls on a metal to produce photoelectron. The electron with maximum kinetic energy are made to move perpendicular to a magnetic field of (1)/(320) T in a radius of 10^(m). The work function of the metal is : |
|
Answer» 3.03 eV `(1)/(lambda)=R((1)/(2^(2)))-(1)/(3^(2))=(5R)/(36)` Given `r=10^(-3) m and B=(1)/(320)T` Now `r=(mv)/(EB)=(sqrt(2mk))/(eB)` Here K is K.E. of emitted electron `:.K=(r^(2)e^(2)B^(2))/(2m)` `=(10^(-6)xx(1.6xx10^(-19))^(2)XX1)/(2XX(9.1xx10^(-31))^(2)(320)^(2))=(10^(-17))/(8xx9.1)` `=(10^(-17))/(72.8xx1.6xx10^(-19))eV=0.86eV` Now `(HC)/(lambda)=K+w` `:.w=(hc)/(lambda)-K` `=(5Rhc)/(36)-K` `=(5xx13.6)/(36)eV=0.86eV` ` w=103.eV` is work FUNCTION of metal |
|
| 41974. |
An alternating sinusoidal current of frequency omega=1000s^(-1) flows in the winding of a straight solenoid whose cross - sectional radius is equal to R=6.0 cm. Find the ratio of peak values of electric and magnetic energies within the solenoid. |
|
Answer» Solution :Here `I = I_(m) COS omegat`, then the peak magnetic energy is `W_(m) = (1)/(2)LI_(m)^(2) = (1)/(2)mu_(0)n^(2)I_(m)^(2)piR^(2)d` Changing magntic field induces an electric field which by Fararday's law is given by `E.2pi R =- (d)/(dt) int oversetrarr(B).d oversetrarr(S) = pir^(2) mu_(0)nI_(m)omega SIN omega t` `E = (1)/(2)rm_(0)nI_(m)omega sin omega t` The associated peak electric energy is `W_(e) = int (1)/(2)epsilon_(0)E^(@)d^(3)r = (1)/(8)epsilon_(0)mu_(0)^(2)n^(2)I_(m)^(2)omega^(2)sin^(2)omega xx (piR^(4))/(2)d` Hence `(W_(e))/(W_(m)) = (1)/(8) epsilon_(0)mu_(0) (omegaR)^(2) = (1)/(8)((omegaR)/(c))^(2)` Again we expect the results to be valid if and only if `((omegaR)/(c)) lt lt 1` |
|
| 41975. |
If oint_(s)vecE.vecdS=0 over a surface, then |
|
Answer» the electric field inside the surface and on it is zero. `ointvecE.vec(dS)=0` Means no. of electric field lines EMERGE out is equal to no. of electric field lines emerge in. According to Gauss.s law, CHARGE enclosed by the surface should be zero. Hence, other charges should be outside the surface as they are not CONSIDERED in flux. |
|
| 41976. |
An ammeter A of finite resistance, and a resistor R are joined in series to an ideal cell C. A potentiometer P is joined in parallel to R. The ammeter reading is I_(0) and the potentiometer reading is V_(0) . P is now replaced by a voltmeter of finite resistance. The ammeter reading now is I and the voltmeter reading is V. |
|
Answer» `I GT I_(0), V LT V_(0)` |
|
| 41977. |
A particle ofmass 0.1 kg is executing S.H.M. with amplitude 0.1 m. At the mean position its K.E. is 8xx10^(-3) J. If the intial phase is 45^(@). What is the equation of its motion ? |
|
Answer» `y=0.1 sin(4t)` `(1)/(2)m omega^(2)A^(2)=8xx10^(-3)" J"` or `(1)/(2)xx(0.1)^(2)xx0.1xx omega^(2)=8xx10^(-3)` `omega^(2)=16` or `omega=4` rad `s^(-1)` and `phi=(+pi)/(4)`or `y=0.1sin(4t+(pi)/(4))`. Correct CHOICE is (b). |
|
| 41978. |
The force experienced by a particle having mass m and charge q accelerated through a potential difference V when it is kept under perpendicular magnetic field vec(B) is .............. . |
|
Answer» `SQRT((2Q^(3) BV)/(m))` |
|
| 41979. |
Photons of 5.5 eV energy fall on the surface of the metal emitting photoelectrons of maximum kinetic energy 4.0 eV. The stopping voltage required for these electrons is |
|
Answer» 5.5 V |
|
| 41980. |
A particle of mass 2 is dropped from a height 80 m above the ground. At the same time another particle of mass m is thrown vertically upwards from the ground with a speed of 40 m/s. If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of second is: |
|
Answer» `((sqrt(112)-2)/(3))` at collision , `v_(A) = 20"" v_B = - 20` Velocity of combined mass `= (2 m XX 20-m xx 20)/(2m + m) = (20)/(3)` m/s Time taken by combined mass to rach the ground Time `=((sqrt(112)-2)/(3))` sec. 
|
|
| 41981. |
Obtain an expression for motional emf from Lorentz force. |
|
Answer» Solution :Consider a straight conducting rod AB of length 1 in a uniform MAGNETIC field `vec(B)` which is directed perpendicularly into the plane of the paper as shown in Figure (a). The length of the rod is normal to the magnetic field. Let the rod move with a constant velocity `vec(v)` towards right side. ii. When the rod moves, with same velocity `vec(v)" in "vec(B).` As a result, the DIRECTION from B to A and is given by the relation `vec(F_(B))=-e(vxxvec(B))` iii. The ACTION of this Lorentz force is to accumulate the FREE electrons at the end A. This accumulation of free electrons produces a potential difference across the rod which in turn establishes an electric field `vec(E)` directed along BA (Figure (b)). Due to the electric field `vec(E)`, the coulomb force stars acting on the free electrons along AB and is given by `vec(F_(E))=-evec(F)` iv. The magnitude of the electric field `vec(E)` keeps on increasing as long as accumulation of electrons at the end A continues. The force `vec(F_(B))` also increases until equilibrium is reached. At equilibrium, the coulomb force `vec(F_(E))` balance each other and no further accumulation of free electrons at the end A takes place.  v. The potential difference between two ends of the rod is V = El V = vBl `vec(B)(botr," inwards ")`  vi. Thus the Lorentz force on the free electrons is responsible to maintain this potential difference and hence produces an emf `epsilon=B//v` vii. As this emf is produced due to the movement of teh rod, it is often called as motional emf. |
|
| 41982. |
Can we take one slab of p-type semiconductor and physically join it to another n-type semiconductor to get p-n junction? |
| Answer» SOLUTION :No! Any SLAB, howsoever FLAT, will have roughness much larger than the inter-atomic crystal spacing (~2 to 3 Å) and hence continuous contact at the atomic level will not be possible. The junction will behave as a discontinuity for the flowing charge carriers. | |
| 41983. |
Explain the term 'drift velocity' of electrons in a conductor. Hence obtain the expression for the current through a conductor in terms of 'drift velocity'. |
|
Answer» Solution :Drift velocity of electrons in a conductor : METALS contain a large number of free electrons. These electrons are in continous random motion. Due to the random motion, the free electrons COLLIDE with positive metal ions with HIGH frequency and undergo change in direction at each collision. So, the average velocity for the electrons in a conductor is zero. Now, when this conductor is connected to source of EMF, an electric field is established in the conductor such that `E = (V)/(L)` Where V = potential difference across the conductor and L = length of the conductor. The electric field exerts an electrostatic force "-Ee" on each free electron in the conductor. The acceleration of each electron is given by`vec(a) = -(e vec(E))/(m)` Where, e = electric charge on the electron and m = mass of electron The negatice sign indicates that the force and hence the acceleration is in a direction opposite to the direction of the electric field. Dueto this acceleration, the electrons attain a velovity in addition to thermal velocity in the direction opposite to that of electric field. The average velocity of all the free electrons in the conductor is called the drift velocity of free electrons of the conductor. `vec(V)d = (e vec(E))/(m)tau""...(i)` Thus, the expression for the drift velocity is electric field, `E = (-V)/(L)""...(ii)` where `tau` = relaxation time between two successive collisions. Let n = number DENSITY of electrons in the conductor. No. of free electrons in the conductor = nAL Tolal charge on the conductor, q = nALe Time taken by this charge to cover the length L of the conductor, `t = (L)/(V_(d))` Current `""I = (q)/(t) = (nALe)/(L) xx V_(d) = nAeV_(d)` Using equation (i) and (ii), we get `I = nAe xx (-(e vec(E))/(m)tau)=nAe xx (-(e(-v))/(mL)tau)=(("ne"^(2)A)/(mL)tau)V`. |
|
| 41984. |
A ray of light having wavelenght 720 nm enters in a glass of refractive index 1.5 The wavelenght of the ray within the glass will be |
| Answer» Solution :`lambda_(G) = (lambda_(o))/(mu) = (790 nm)/(1.5) = 480 nm` | |
| 41985. |
The physical quantity which has same dimensions as that of Planck's constant is |
| Answer» SOLUTION :ANGULAR MOMENTUM | |
| 41986. |
If n is the orbit number of the electron in a hydrogen atom, the correct statement among the following is : |
|
Answer» electron ENERGY varies as `n^(2)` Hence, electron energy increases as n increases |
|
| 41987. |
(A): Material used in the construction of a standard resistance is constantan or manganin. (R): Temperature coefficient of Resistance constantan is very small. |
|
Answer» Both 'A' and 'R' are true and 'R' is the correct EXPLANATION of 'A' |
|
| 41988. |
For a full scale deflection in a galvanometer,a current of 50mA is required. The resistance of galvanometer is 99Omega if it is converted into an ammeter of 5 A range, the necessary shunt resistance should be : |
|
Answer» `1.0Omega` |
|
| 41989. |
The particular used for transmission of light signal through opticalfibe is |
|
Answer» TOTAL INTERNAL reflection |
|
| 41990. |
If the number of turns in a galvanometer becomes double. Then deflection for the same current will become: |
|
Answer» HALF |
|
| 41991. |
Assume that the nuclear binding energy per nucleon (BIA) versus mass number (A) is as shown in the figure. Use this plot to choose the correct choice(s) given below: |
|
Answer» Fusion of two NUCLEI with mass mumber lying in the range of `1 LT A lt 50` will release energy. (a) For `1 lt A lt 50`, on fusion mass number of the resulting nucleus will be less than 100. (b) For `51 lt A lt 100`, on fusion mass number of the resulting nucleus is between 100 and 200. B/A increases, energy will be released. (c) On fission for `100 lt A lt 200`, the mass number for fission nuclei will be between 50 to 100. B/A decreases, no energy will be released. (d) On fission for `200 lt A lt 260`, the mass number for fission nuclei will be between 100 to 130, B/A will increase, energy will be released. |
|
| 41992. |
A block of mass m is pulled along a horizontal suface by applying a force at an angle q with the horizontal. If the block travels with a uniform velocity and has a displacement d and the coefficient of friction is mu, then the work done by the applied force is |
|
Answer» `(MU m gd)/(cos theta + mu sin theta)` |
|
| 41993. |
In the circuitshown here current flowing through 3Omega resistor is_____ . |
| Answer» Solution :1A. Here CURRENT flowing through 3`OMEGA` resistance, `I = epsi/R = (3V)/(3Omega) = 1A` | |
| 41994. |
For a point on the axis of the electric dipole theta = 0 and theta = pi = .. .. .. .. . , ......... |
|
Answer» `-(KP)/(r^(2)),+(kP)/(r^(2))` `:. V =pm = (kP)/(r^(2))` |
|
| 41995. |
The minimum energy required to excite a hydrogen atom from its ground state is ______. |
| Answer» Solution :10.2 EV.[MINIMUN ENERGY required [` E = E_(2) - E_(1) = - (13.6)/((2)^(2)) - (13.6)/((1)^(2)) = - 3.4 + 13.6 = + 10.2eV`]. | |
| 41996. |
Discuss the basic properties of electric charges. |
|
Answer» SOLUTION :(i) Electric charge : Most objects in the universe are made of atoms which in turn are made up of protons neutrons and electrons. These particles have mass an inherent property of particles . Similarly the electric charge is another intrinsic and fundamental property of particles . The SI unit of charge is coulomb . (ii) Conservation of charges : Benjamin Franklin argued that when one object is rubbed with another object charges get transferred from one to the other . Before rubbing both objects are electrically neutral and rubbing simply transfers the charges form one object to the other . (For examplewhen a glass rod is rubbed against silk cloth some negative charge are transferred from glass to silk . As a result the glass rod is positively charged and silk cloth becomes negatively charged ) . From these observations he concluded that charges are neither created or nor destroyed but can only be transferred from one object to other . This is called conservation of total charges and is one of the fundamental conservation laws in physics . It is stated more generally in the following way . The total electric charge in the universe is constant and charge can neither be created nor be destroyed . In any physical process the net change in charge will always be zero. (iii) Quantisation of charges : The charge q on any object is equal to an integral multiple of this fundamental unit of charge e. q=ne Here n is any integer `(0,pm1,pm2,PM3,PM .... ).` This is called quantisation of electric charge . Robert Millikan in his famous experiment found that the value of e `= 1.6xx10^(-19)C.` The charge of an electron is `-1.6xx10^(-19)C` and the charge of the proton is `+1.6xx10^(-19)C` . When a glass rod is rubbed with silk cloth the number of charges transferred is usually very large typically of the order of `10^(10)` .So the charge quantisation is not appreciable at the macroscopic level . Hence the charges are treated to be continuous ( not discrete ) . But at the microscopic level , quantisation of charge PLAYS a vital role. |
|
| 41997. |
Two coherent monochromatic point sources S_1 and S_2 of wavelength lambda = 600 nm are placed symmetrically on either side of the centre of the circle as shown. The sources are separated by a distance d = 1.8 mm. This arrangement produces interference fringes visible as alternate bright and dark spots on the circumference of the circle. The angular separation between two consecutive bright spots is Delta theta. Which of the following options is/are correct ? |
|
Answer» The TOTAL number of fringes produced between `P_1 and P_2` in the first quadrant is close to 3000 `n = d/(lambda) = (1.8 XX 10^(-3))/(600 xx 10^(-9)) = 3000` We can see that option (a) is correct. Moreover path difference at point P is integral (n = 3000) multiple of wavelength, hence there will be bright at the point `P_2`. Hence option (b) is not correct but option (c ) is correct. We shall now calculate path difference between waves arriving at point P from the two sources and for this calculation we shall assume that radius of the circle is much greater than the separation between sources. OP makes an angle `theta` with the line joining sources. Since radius is very large, we can treat lines `S_1P, OP and S_2P` almost parallel to each other. M is the foot of perpendicular drawn from `S_2`on`S_1P`. Path difference `(X) = S_2P - S_1P ~~ S_1M` Angle `MS_1S_2` is also approximately `theta`, hence in triangle `MS_1S_2` we can write the following: `cos theta = (S_1M)/(S_1S_2)` `implies cos theta = x/d implies x = d cos theta` We can differentiate the above relation. `(dx)/(d theta) = -d sin theta implies (Delta x)/(Delta theta) = - d sin theta` `implies Delta x = -(d sin theta) Delta theta` `Deltax` is the difference prodced in the path difference as we move further by an angle `Delta theta`. For consecutive fringes, difference in path difference MUST be `lambda`. Hence if we assume `Delta x` equal to `lambda`, then `Delta theta` will be the angular fringe width. Hence angular fringe width can be written as follows: `implies |Delta theta| = lambda/(d sin theta)` As we move from `P_1` towards `P_2`, value of `theta` decreases from `90` to `0`, hence `sin theta` decrease which means angular fringe width `Delta theta` increases. 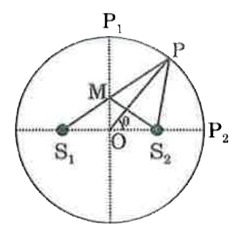
|
|
| 41998. |
A five- wire potentiometer is connectedto an accumulator emf 2.2 V and internal resistance 1 Omega The potentiometer wire has resistance of 1 Omega per metre. What is the maximum voltage that you can measure with this particular arrangement of the potentiometer? What length of this potentiometer will balancethe emf of a Daniell cell(emf=1.18)? What resistance in series with the accumulatro will be required to balce this cell exactly at the centre of the last wire? |
|
Answer» |
|
| 41999. |
A magnifying glass is made of a combination of a convergent lens of power 20D and and divergent lens of power 4D. If the least distance of distinct vision is 25cm. The magnifying power is |
|
Answer» 7 |
|