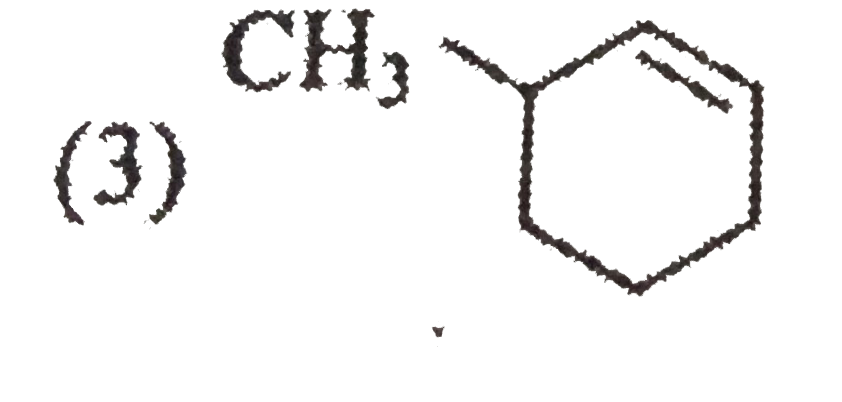Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 42001. |
Monochromatic light of frequency 6.0xx10^(14) Hz is produced by a laser.The power emitted is 2.0xx10^(-3) W. (a)What is the energy of a photon in the light beam?(b)How many photons per second.on an average ,are emitted by the source? |
| Answer» Answer :B | |
| 42002. |
Calculate the limit of resolution of a telescope given that the diameter of the objective is 1.5 m and wavelength of the light used is 555 nm. |
|
Answer» SOLUTION :`d theta= ( 1.22 LAMBDA)/( D)` `d theta =(1.22 XX 555 xx 10^(-9) )/( 1.5) = 4.514 xx 10^(-7) rad` |
|
| 42003. |
If a high power heater is connected to electric mains, then the bulbs in the house become dim, because there is a |
|
Answer» CURRENT DROP |
|
| 42004. |
A conductro AB carrying current i is placed vertically above and parallel to a long horizontal conductor XY carrying current I. Assume that AB is free to move and that the wires through which currents enter and leave it do no exert any forces on it. If AB is in equilibrium |
|
Answer» `i=I` |
|
| 42005. |
Which one is the correct spelling? |
|
Answer» INDENTITI |
|
| 42006. |
An object is kept at rest on the principal axis of a lens. Initially the object is at a distance three times the focal length 'f' of the lens. The lens runs towards the object at a constant speed u, until the distance between the object and its real image becomes 4 f. If the iamge always forms on a moving screen then express the velocity of the screen as a function of time. |
|
Answer» `u("x-co-ordinate of object")=-[3 F-u t]` by lens FORMULA `rArr(1)/(v)-(1)/(u)=(1)/(f)` `rArr (1)/(v)=(1)/(f)+(1)/(u)=(1)/(f)+(1)/(-(3f-u t))` `=(-3f+u t+f)/(f(3f-u t)), v=(f(3f-u t))/(u t- 2f)`  Now by differentiating the lens formula once we get `v_(iL)=(v^(2))/(u^(2))v_(oL) rArrv_(i)-v_(L)=(f^(2)(3f-u t)^(2))/((ut-2f)^(2))xx(1)/((3f-ut)^(2)).(v_(o)-v_(L))` `=u+(f^(2))/((ut-2f)^(2))(0-u) =u[1-(f^(2))/((ut-2f)^(2))]` Ans `THEREFORE v_(i)=u[1-{(f)/(ut-2f)}^(2)]` |
|
| 42007. |
A particle of mass m and charge Q is placed in an electric field E which varies with time t ass E = E_(0) sin omegat. It will undergo simple harmonic motion of amplitude |
|
Answer» `(QE_(0)^(2))/(MOMEGA^(2))` |
|
| 42008. |
A : In Y.D.S.E., if distance of screen (D) is very large compared to the fringe width, the fringes will be very nearly straight lies. R : In general, the shape of fringes formed in Y.D.S.E is hyperbola. |
|
Answer» Both A and R are true and R is the correct explanation of A |
|
| 42009. |
यदि a तथा 18 का लघुतम (LCM ) 36 है तथा a और 18 का महतम समापवर्तक (HCF ) 2 है, तो a = |
|
Answer» 2 |
|
| 42010. |
Assertion (A): Bluish colour predominates in a clear sky. Reason( R): Light of shorter wavelengths is scattered much more than light of longer wavelengths. |
|
Answer» If both ASSERTION and reason are TRUE and the reason is the CORRECT EXPLANATION of the assertion. |
|
| 42011. |
Shape of graph drawn between rate of decay and number of radio active nuclei is |
|
Answer»
|
|
| 42012. |
230 J work is done in lifting a block of 10 kg to a height of 2 m above the ground. The acceleration of the block (given g=10m//s^(2)) is : |
|
Answer» `23 m//s^(2)` |
|
| 42013. |
In a stationary wave the particle velocity at nodal point is |
|
Answer» Zero |
|
| 42014. |
When a man walks on a horizontal surface with constant velocity work done by the |
|
Answer» frictional force is zero |
|
| 42015. |
Charge passing through the cross-section of a conductor h given by Q = B' + A' t^(2). What will be the current in ampere at lime t = 10 s ? |
|
Answer» 5 A' I= `(dQ)/(dt ) = (d)/(dt)(B. + A. t^(2)) ` `therefore I = 0 + 2A.t ` `therefore I = 2A. XX 10 = 20 A.` |
|
| 42016. |
An electric current flows in a wire from eastto west- What will be the direction of the magnetic field due to this wire at a point north of the wire? South of the wire? |
| Answer» SOLUTION :VERTICALLY UPWARDS, vertically DOWNWARDS | |
| 42017. |
A child is sitting on a swing. Its minimum and maximum heightsfrom the groundare 0.75 m and 2m respectively. Its maximum speed willbe : |
|
Answer» 10 m/s `v=sqrt(2g(2-0.75))=sqrt(2xx10xx1.25)=5" ms"^(-1)` CORRECT CHOICE is ( c ). |
|
| 42018. |
A galvanometer of resistance 150 ohm is shunted such that only 1/11 of the main current flows through the galvanometer. The resistance of the shunt is, (in ohm) |
|
Answer» 5 |
|
| 42019. |
AC = CO = D , S_(1) C = S_(2) C = d ltlt D A small transparent slab containing material of mu = 1.5 is placed along AS_(2). What will be the distance from O of the principal maxima |
|
Answer» `D/4` `therefore ` For principal maxima `2d sin theta + 0.5 l = 0` `sin theta_(0) = (-l)/(4d) = (-1)/(16)(because l = (d)/(4))` `therefore` OP = D `TAN theta_(0) = -(D)/(16)` |
|
| 42020. |
Resistance of platinum wire in one platinum resistance thermometer at ice point and at steam point are respectively 10 Omega and 10.78 Omega. When this thermometer is kept in one heat bath, its resistance is found to be 10.123 Omega. Find temperature of this heat bath in degree Fahrenheit (""^(@)F). |
| Answer» SOLUTION :`THETA = 23.34 " "^(@)F ` | |
| 42021. |
The range of ground wave transmission can be increased by |
|
Answer» INCREASING the power of transmitter with the USE of HF |
|
| 42022. |
A bob is suspended from an ideal string of length 'l'. Now it is pulled to a side through 60^(@) to vertical and whirled along a horizontal circle. Then its period of revolution is |
|
Answer» `PI sqrt((L)/(g))` |
|
| 42023. |
Newton's second law for translation motion in the xy plane is sumvec(F) = mvec(a) ,Newton's second law for rotation is sumT_(x) = lalpha_(x) . Consider the case of a particle moving in the x-y plane under the influence of a single force. |
|
Answer» Both `vec(F) = m vec(a) ` and `T_(X) = I alpha_(x)` MUST be USED to analyze the motion of this PARTICLE . |
|
| 42024. |
Equations a stationary and a travelling waves are as. follows y_(1) = a sin kx omega tand y_(2) = a sin(wt - kx) . The phase difference between two pojnt x_(1) = pi/(3k) and x_(2) = (3pi)/(2k) are phi_(1) and phi_(2)respectively for the two waves. The ratio phi_(1)/phi_(2) is: |
|
Answer» 1 |
|
| 42025. |
A particle of mass W is projected with a velocity V making an angle of 30° with the horizontal. The magnitude of angular momentum of the projectile about the point of projection when the particle is at its maximum height H is: |
|
Answer» zero `L=pr=mvcostheta.H` `=mvcos30^@xx(v^(2)sin^(2)30^@)/(2g)` `mv^(3)xxsqrt(3)/2XX1/(4xx2g)=(sqrt(3)mv^(3))/(16g)` |
|
| 42026. |
An air parallel plate capacitor having a capacitance C is charged by connecting it to a battery . Now it is disconnected from the battery and a dielectric constant K is inserted between its plates so as to completely fill the space between the plates compare : (i) Initial and final capacitance . (ii) Initial and final charge. (iii) Initial and final potential difference. (iv) Initial and final electric field between the plates . (v ) Initial and final energy stored in the capacitor |
|
Answer» Solution :(i) Initial capacitance = C Final capacitance = KC ( after INSERTING dielectric ) `implies (C_(1))/(C_(i))= K` (ii) Charge on isolated capacitor remains same therefore `(Q_(t))/(Q_(i))` =1 (iii) As `Q= CVimplies V = (Q)/(C ) implies (V_(t))/(V_(t))= (C_(i))/(C_(t))= (1)/(K)` (iv) `E=(V)/(d) implies (E_(1))/(E_(i))=(V_(t))/(V_(i))=(1)/(K)` `U= (Q^(2))/(2C) implies (U_(r))/(U_(t))=(C_(i))/(C_(r))=(1)/(K)` |
|
| 42027. |
Explain Young's double slit-experiment. |
Answer» Solution :Young.s DOUBLE slit apparatus consists of a narrow rectangular slit S. It is illuminated by a monochromatic light. The light emerging from S illuminates the two identical close SLITS `S_1` and `S_2` whichacts as coherent SOURCES . The wave emerging from `S_1` and `S_2`get superposed and interference fringes are produced as SHOWN on the observation screen. Bright fringes are formed on the screen due to the superpositionof crests of two waves or troughs of two waves. Dark friges are formed due to the superposition of crest and trough of two waves. At the CENTRE of the screen always bright fringe is formed. This is because , all the waves meeting at the centre of the screen have the zero path difference and zero phase difference. 
|
|
| 42028. |
How much positive and negative charge is there in a cup of water ? |
|
Answer» SOLUTION :Mass of water in a cup can be taken approximately 250 g (which actually should havebeen given in the statement). In one molecule of water, there are 2 hydrogenatoms and 1 oxygen atom. Hence, in one molecule of water there are 2 + 8 = 10 protons and 2 + 8 = 10 ELECTRONS. Let it be x. If there are N no. of water molecules in a given mass then magnitude of its positive charge (or NEGATIVE charge) would be, Q = Nxe ... (1) If no. of moles of water molecules is \i then wehave, `mu = M/M_(0) = N/N_(A) rArr N = (MN_(A))/M_(0)`.......(2) where M = given mass of water = 250g `M_(0)` = molar mass of `H_(2)O` molecules (`2 xx` molar mass of H-atoms) + (molar mass of O-atom) = 2(1) + 16 = 18 g/mol N= TOTAL no. of water molecules `N_(A)`= Avogadro number From equation (1) and (2) `Q = (MN_(A))/M_(0).xe` `therefore Q =(250 xx 6.02 xx 10^(23) xx 10 xx 1.6 xx 10^(-19))/18` `therefore Q = 1.338 xx 10^(7)` C |
|
| 42029. |
At what angle with the magnetic meridian will a magnetic needle rest if it is subjected to a magnetic field of induction0.6 xx 10^(-4)T perpendicular to the magnetic meridian? (B_H=0.2 xx 10^(-4)T) |
| Answer» SOLUTION :`71^(@) 34^(1)` | |
| 42030. |
During a nuclear fusion reaction : |
|
Answer» A heavy nucleus breaks into TWO fragments by itself |
|
| 42031. |
Figure shows a plot of where V is the accelerating potential. The de-Broglie wavelength 'λ' in the case of two particles having same charge 'q' but different masses m, and mz. Which line (A or B) represents a particle of larger mass ? |
|
Answer» Solution :`LAMBDA=(h)/(sqrt2meV)` `lambda_(A)=(h)/(sqrt2m_(A)qV_(A))` `lambda_(B)=(h)/(sqrt2Me_(B)eV_(B))=(h)/(sqrt2M_(B)qV_(B))` `SQRT((2m_(B)qV_(B))/(2m_(A)qV_(A)))=sqrt((m_(B)V_(B))/(m_(A)V_(A)))` `(lambda_(A))/(sqrtV_(A))=(lambda_(B))/(sqrtV_(B))` `m_(A)< m_(B)` |
|
| 42032. |
In the above question, if the string C is strucjed slowly then: |
|
Answer» The PORTION AB of the STRING will BREAK |
|
| 42033. |
A ray of light parallel to the principal ads of a spherical mirror falls at a point M as shown In the figure.If the mirror is immersed in water its focal length will be |
|
Answer» LESS than 10cm |
|
| 42034. |
How is the Shehnai different from the Pungi? |
|
Answer» SHEHNAI has a BETTER sound |
|
| 42035. |
A sperical capacitor composed of two concentric metal spheres one having a radius twice as large as the other. The region in which the energy is stored has a volume of |
|
Answer» `1/4c^3/(pi^2epsilon_0^2)` |
|
| 42036. |
Mahavira is said to have lived here for |
|
Answer» 14 years. |
|
| 42037. |
An alpha-particle with kinetic energy T_(alpha)= 7.0MeV is scattered elastically by an initially stationary Li^(6) nucleus. Find the kinetic energy of the recoil nucleus if the angle of divergence of the two particle is Theta= 60^(@). |
|
Answer» Solution :Initial momentum of the `alpha` particle is `sqrt(2mT_(alpha)) hat(i)` (where `hat(i)` is a unit vector in the incident direction.) Final momenta are RESPECTIVELY `vec(p)_(alpha)` and `vec(p_(LI)`. Conservation of momentum reads `vec(P)_(a)+vecP_(Li)= sqrt(2mT_(alpha))hat(i)` Squarting `p_(alpha)^(2)+p_(Li)+2p_(alpha)p_(Li)COS Theta= 2mT_(alpha)` (1) where `Theta` is the angle between `vec(p)_(alpha)` and `vec(p)_(Li)`. ALSO by energy conservation `(p_(alpha)^(2))/(2m)+(p_(L)^(2))/(2M)=T_(alpha)` (`m & M` are respectively the masses of `alpha` particle and `Li^(6)`.)So `p_(alpha)^(2)+(m)/(M)p_(Li)^(2)= 2mT_(alpha)` (2) Substituting (2) from (1) we see that `P_(Li)[(1-(m)/(M))p_(Li)+2p_(alpha)cos Theta]=0` Thus if `p_(Li) ~~ 0` `p_(alpha)= -(1)/(2)(1-(m)/(M))p_(Li)sec Theta`. Since `p_(alpha), p_(Li)` are both positive number (being magnitudes of vectors) we must have `-le cos Theta lt 0 if m lt M` This being understood, we write `(P_(Li)^(2))/(2M)[1+(M)/(4m)(1-(m)/(M))^(2) sec^(2)Theta]=T_(alpha)` Hence the recoil energy of the `L_(i)` nucleus is `(P_(Li)^(2))/(2M)=(T_(alpha))/(1+((M-m)^(2))/(4mM)sec^(2)Theta)` As we pointed out above `Theta ~~ 60^(@)`. If we take `Theta= 120^(@)`, we get recoil energy of `Li= 6MeV`. |
|
| 42038. |
A calorimeter of negligible heat capacity contains 100 gm water at 40^(@)C. The water cools to 35^(@)C. in 5 minutes. If the water isnow replaced bya liquid ofsame volume as that of water at same initial temperature, it cools to 35^(@)C in 2 mintues. Given specific heats of water and that liquid are 4200J//Kg""^(@)C. and 2100J//Kg""^(@)C respectively. Findthe density of the liquid. |
|
Answer» Solution :Using average form of Newton's law of cooling, we USE For water `(40-35)/(5) =(K)/(0.1 XX 4200)((40+35)/(2)-T_(s))`…(1) For liquid `(40-35)/(2) =(k)/(m xx 2100)((40+35)/(2)-T_(s))` ..(2) `((1))/((2))` gives `(2)/(5) = (mxx 2100)/(0.1 xx 4200)` `rArr m =(2 xx 420)/(5 xx 2100) = 0.08 kg = 80 gm` As the volume of liquid is same that of water `100 cm^(3)`, then density of liquid is `P =(m)/(V) =(80 xx 10^(-3))/(100 xx 10^(-6)) = 800 kg//m^(3)` |
|
| 42039. |
A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field (a) outside the toroid, (b) inside the core of the toroid, and (c) in the empty space surrounded by the toroid. |
| Answer» Solution :B for a toroid is given by the same formula as for a SOLENOID: `B = mu_0 nI`, where n in this CASE is given by `n = (N)/(2pi r)` . The field is non-zero only inside the core surrounded by the windings. (a) Zero, (b) `3.0 x× 10^(-2)` T, (c) zero. Note, the field varies SLIGHTLY across the cross-section of the toroid as r varies from the inner to outer radius. Answer (b) corresponds to the mean radius r = 25.5 CM. | |
| 42040. |
Two bodies having the same mass 2kg each have different surface areas 50m^2 and 100 m^2 in contact with a horizontal plane. If the coefficient of friction is 0.2, the forces of friction that come into play when they are in motion will be in the ratio |
| Answer» ANSWER :A | |
| 42041. |
In the following circuit, 5 Omegaresistor develops 45 J/s due to current flowing through it. The power developed across 12 Omegaresistor is |
| Answer» Answer :B | |
| 42042. |
Figure shows a small block suspended vertically using an ideal spring. Initially spring is in natural length nad the mass is 1 mm above the principal axis of a concave mirror whose focal length is 20cm. Given that mass m=10 grams, k=100N//m, g=10m//s^(2). the amplitude of the image of the block formed by concave mirror is A millimetres, find the integer value 'A' |
|
Answer» `1/v+(1/(-30))=(-1)/20` `impliesv=-60cm` Magnification `m=-v/u=-2` This, amplitude of image `=2MM`. |
|
| 42043. |
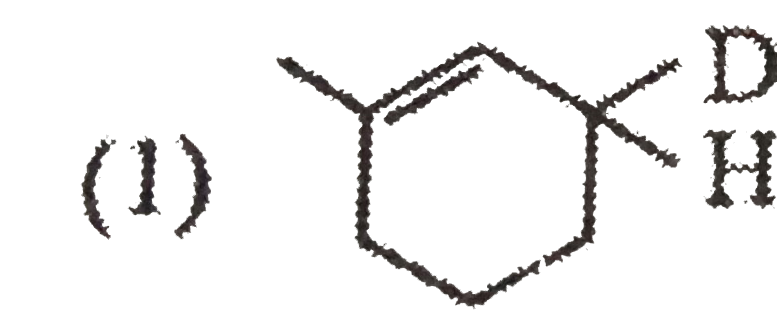
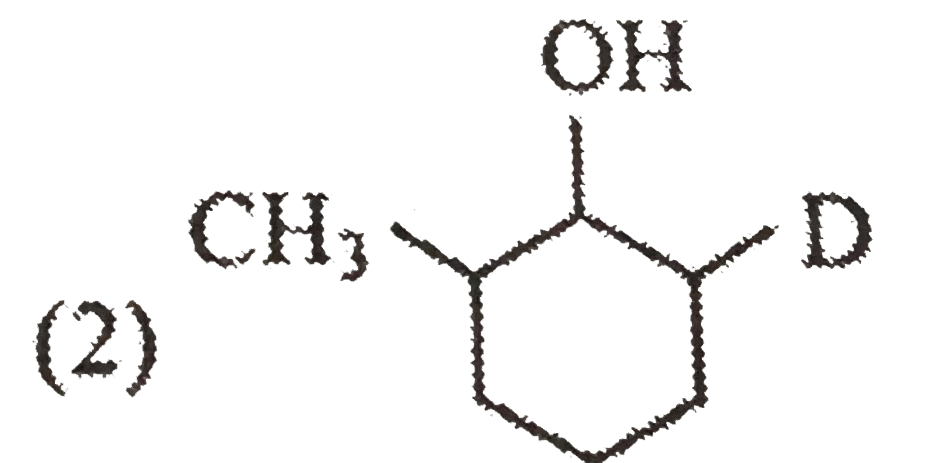
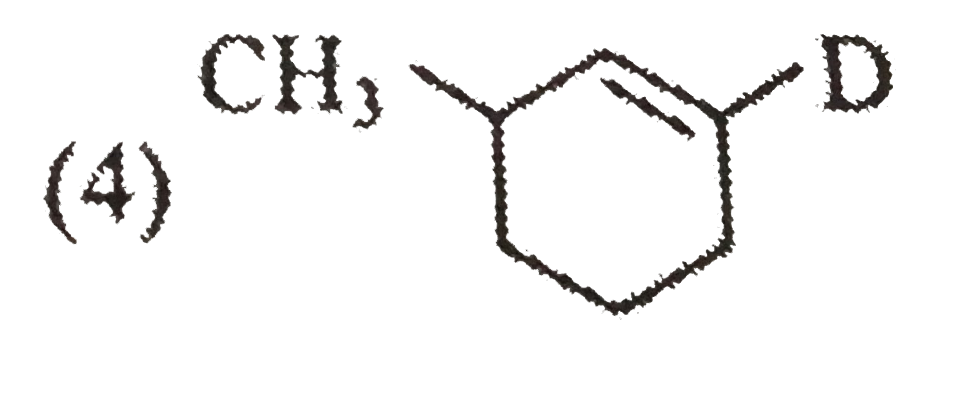
Major product of this reaction is : |
|
Answer»
|
|
| 42044. |
We know that magnetic substances follow curie- weiss Law. In the given table, Column I shows the type of attraction with magnets of magnetic substances, Column II shows the example of magnetic substances and Column III shows the three figures- figure (I) shows direction of magnetic momentum of each electron when there is no magnetic field inside magnetic substance, figure (II) shows the direction of magnetic momentum of electron when there is magnetic field inside magnetic substance and figure (III) shows the curve between M and H inside magnetic substance. Which combination is characteristic of paramagnetic materials ? |
|
Answer» (I)(II)(L) |
|
| 42045. |
Find the potential difference between the points A and B in the circuit shown in Fig. 4.66. Internal resistances of the cells are negligible. |
|
Answer» |
|
| 42046. |
The spectral line in the spectrum of light from a star is found to be shifted by 0.032% from its normal position towards the red end of the spectrum . Compute the velocity of the star. |
|
Answer» |
|
| 42047. |
The binding energy per nucleon is maximum at A=56 and its value is around ____ Mev/ Nucleon |
|
Answer» 8.4 |
|
| 42048. |
We know that magnetic substances follow curie- weiss Law. In the given table, Column I shows the type of attraction with magnets of magnetic substances, Column II shows the example of magnetic substances and Column III shows the three figures- figure (I) shows direction of magnetic momentum of each electron when there is no magnetic field inside magnetic substance, figure (II) shows the direction of magnetic momentum of electron when there is magnetic field inside magnetic substance and figure (III) shows the curve between M and H inside magnetic substance. Which combination is characteristic of diamagnetic materials ? |
|
Answer» (III)(i)(L) |
|
| 42049. |
A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 9.4 cm. What is the refractive index of water? If water is replaced by a liquid of refractive index 1.63 up to the same height, by what distance would the microscope have to be moved to focus on the needle again? |
|
Answer» `mu=1.33,d=1.7 CM` |
|
| 42050. |
For given metal plate threshold frequency is V_(0). When radiation of 2V_(0) is incident on metal surface ,maximum velocity of photoelectron emitted is V_(1) when frequency of incident radiation is charged to 5V_(0) ,maximum velocity of photoelectron emitted is v_(2).Ration of v_(1) and v_(2) is ..... |
|
Answer» Solution :From Einstein equation `(1)/(2)mv_(1)^(2)=h(2v_(0))-hv_(0)` `therefore (1)/(2)mv_(1)^(2)=hv_(0)`…..(1) and `(1)/(2)mv_(1)^(2)=h(5v_(0))-hv_(0)` `(1)/(2)mv_(2)^(2)=4hv_(0)`……..(2) `therefore` TAKING ratio of (1) and (2) , `((v_(1)^(2))/(v_(2)^(2)))=(1)/(4)` `therefore (V_(1))/(v_(2))=SQRT((1)/(4))=(1)/(2)` `therefore` Ratio of `v_(1)` and `v_(2)` is 1:2 |
|