Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 6201. |
SI Unit of Solid angle is- |
|
Answer» Degree |
|
| 6202. |
The length of a second's pendulum is 1 m on the earth. If the mass and diameter of a planet than that of earth, then the length of the second's pendulum on the planet will be |
|
Answer» 4m `THEREFORE 2 = 2pi sqrt((l)/(g))` on the surface of the earth `""` …….(1) On the planet `2=2pi sqrt((l')/(g'))""` …….(2) `therefore (l)/(g)=(l')/(g') "" therefore ""l'=l((g')/(g))""`......(3) But `g=(GM)/(R^(2)) "" therefore ""(g')/(g)=(GM')/(R'^(2))xx(R^(2))/(GM)""` `= 2xx((1)/(2))^(2)=(1)/(2)""` .....(4) `therefore l'=l xx (1)/(2)=(1)/(2)m = 0.5 m` |
|
| 6203. |
The perpendicular of the vector vecF=4hati-3hatj is |
|
Answer» 4i+3j |
|
| 6204. |
A semiconductor diode designed to operate in breakdown region is called : |
|
Answer» tunnel DIODE |
|
| 6205. |
The flux linked with each turn of coil is 0.1 Wb and total number of turns is 1000. If current passing through coil is 10 amp, then self inductance of coil is ...... mH |
|
Answer» 0.1 `THEREFORE L=(NPHI)/I` `=(1000xx0.1)/10` =10H `=10xx1000x10^(-3)` H `therefore L=10^4` mH |
|
| 6206. |
Dimensional formula of capacity is : |
|
Answer» `[ML^2T^4A]` |
|
| 6207. |
Whom we call conductor ? |
| Answer» Solution :The solids having high conductivity are called CONDUCTORS. Ex. FE, Cu, AGETC. | |
| 6208. |
There are two concentric metallic shells of negligible thickness of radii 5 cm and 20 cm. The region between the two shells is filled with a medium of thermal conductivity k. The temperature of inner and outer sphere is maintained at 5^(@)C and 10^(@)C respectively. If the heat current flowing from inner to outer sphere is 100 W, find the value of k. |
|
Answer» |
|
| 6209. |
Define the term 'dielectric constant of a medium in terms of capacitance. |
| Answer» Solution :Dielectric constant of a MEDIUM is defined as the ratio of the capacitance of a given parallel PLATE capacitor in the presence of dielectric to its capacitance in the ABSENCE of dielectric. | |
| 6210. |
The field intensities of two points on the axial line of a bar magnet at distances of 10xx 10^(-2) m and 15 xx 10^(-2) m are in the ratio 5.8:1. Find the distance between the two poles of the magnet. |
| Answer» SOLUTION :`12 XX 10^(-2)m` | |
| 6211. |
When the voltage applied to an X-ray tube increased from V_(1) =10 KV to V_(2)=20 KV, the wavelength interval between the K_(a)-line and the short wavelength cut-off of the continuous X-ray spectrum increases by a factor of 3. Find the atomic number of the element of the target. |
|
Answer» |
|
| 6212. |
A parallel beam of light of wavelength 500nm falls on a narrow slit and resulting diffraction pattern is observed on a screen 1m away. It is observed that the first minimum is at a distance of 2.5 mm from the centre of the screen. Find the width of the slit. |
|
Answer» Solution :The distance of the `N^(TH)` minimum from the centre of the screen is, `x_(n)=(nDlambda)/(a)`, where, `D=` distance of SLIT from screen, `lambda=` wavelength of the LIGHT, `a=` width of the slit. `n=1` (For first minimum) Thus, `2.5xx10^(-3)=(1xx1(500xx10^(-9)))/(a)` `impliesa=2xx10^(-4)m` `=0.2mm` |
|
| 6213. |
A transmitter transmits the message in original |
|
Answer» TRUE |
|
| 6214. |
In Fig.(i), a lens of focal length 10 cm is shown. It is cut into two parts and placed as shown in Fig.(ii). An object AB of light 1 cm is placed at a distance of 7.5 cm. The height of the image will be |
|
Answer» SOLUTION :`1/F=1/(f_1)+1/(f_2)=1/10+1/10` `:. F=5 cm` `1/v-1/-7.5=1/(+5)` `:. V=+15 cm` `m=v/u=(+15)/(-7.5)=-2` `I=mO=(-2)(1CM)` `=-2 cm` |
|
| 6215. |
Four very long straight wires carry equal electric currents in the +z direction. They intersect the xy plane at (x,y)=(-a,0),(0,a),(a,0), and (0,-a). The magnetic force exerted on the wire at position (-a,0) is along |
|
Answer» `+y- "AXIS" ` |
|
| 6216. |
Curved surface of a vessel has shape of a truneated cone having semivertex angle 37^(@) Vessel is full of water (density rho=1000 kg//m^(3)) upto a height of 13 cm and is placed on a smooth horizontal plane. Upper surface is opened to atmosphere. A hole of 1.5 cm^(2) is made on curved wall at a height of 8 cm from bottom as shown in figure. Area of water surface in the vessel is large as compared to the area of hole |
|
Answer» Initial velocity of efflux is 1m//sec Rang e `=0.8xx1/10=8` cm :.Rangefrom B `=8cm-8cmxx3/5=3.2cm` `vcostheta t=1/2 G t^(2)=-0.08` `0.6t-5t^(2)=-0.08` `t=(0.6pmsqrt(0.36+4xx5xx0.08))/(2xx10)=(0.6pm1.4)/20=1/10` Horizontal force required `=mvcos37^(@)=rhov^(2)cos37^(@)=1.5xx10^(-4)xx1000xx2xxgxxDeltahxx(4//5)` `=1.5xx2xx(0.05)/100xx4/5=0.12` N 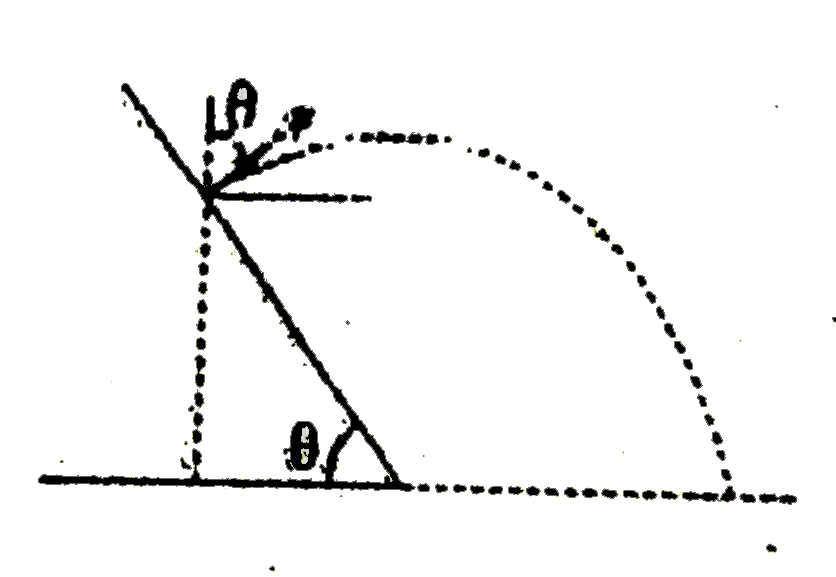
|
|
| 6217. |
Aconvex mirror and a concave mirror each of focal length 10 cm are placed coaxially. The are separated by40 cm and their reflecting surfaces face each other. A point object is kept on the principle axis at a distance x cm from the concave mirror such that final image after two reflections, first on the concave mirror, is on the object itself. Find integer next to x . |
|
Answer» `U=-x` `f=-f` `(1)/(V)=(1)/(f)-(1)/(u)=-(1)/(f)+(1)/(x)rArrv=(fx)/(f-x)` `therefore` Distance of the image from the convex mirror `=4f+(fx)/(f-x)=(4f^(2)-3fx)/((f-x))` `u=-((4f^(2)-3fx))/((f-x))` `f=f` By the question, `v=-(4f-x)``therefore``(1)/(v)=(1)/(f)-(1)/(u) gives` , `(1)/(-(4f-x))=(1)/(f)+((f-x))/((4f^(2)-3fx))` on solving, we GET, `x^(2)-6fx+6f^(2)=0` which gives, `x=(3+-sqrt3)f` But `xlt4f` Hence, `x=(3-sqrt3)10 cm=12.68 cm` 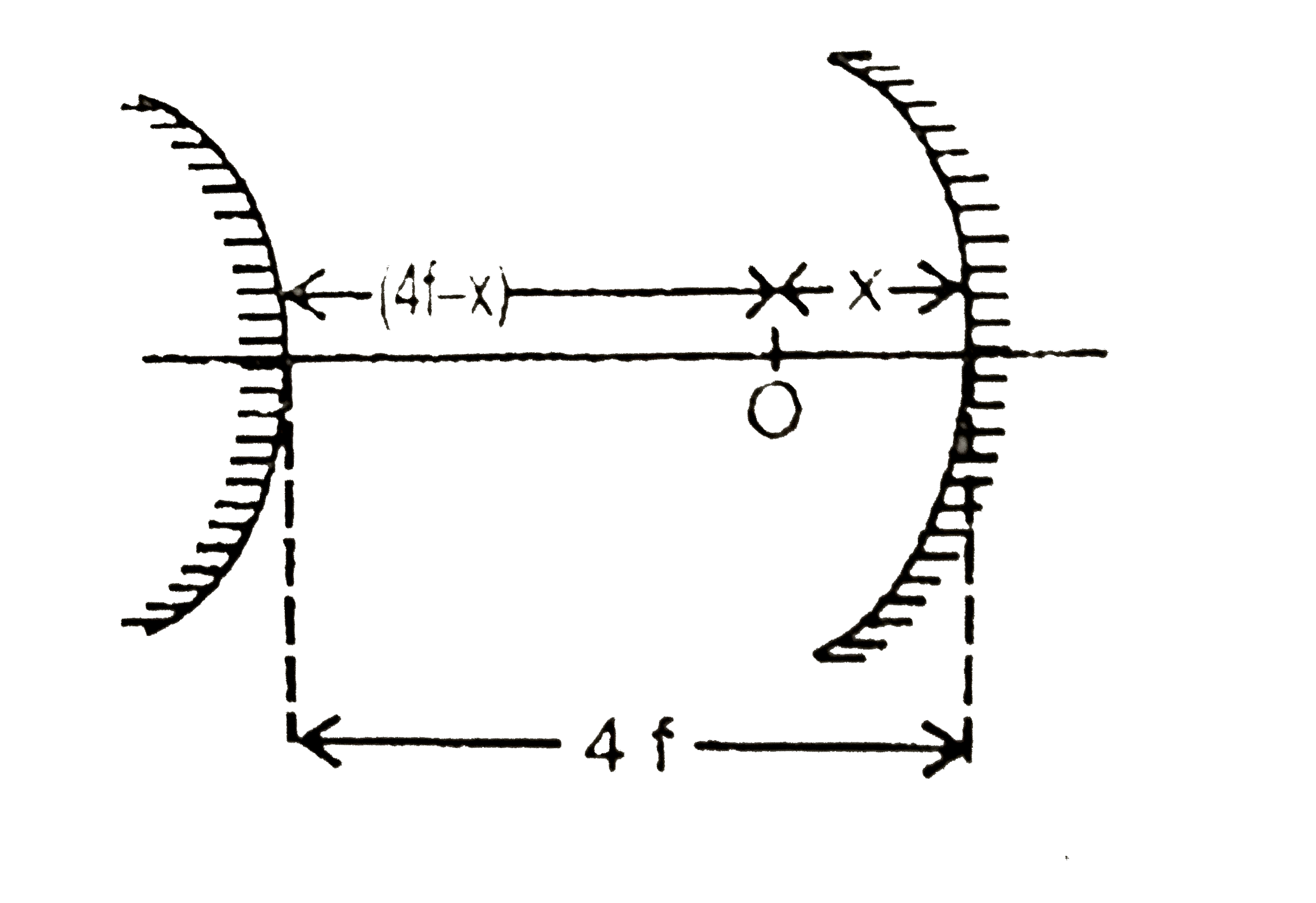
|
|
| 6218. |
A bullet fired into a target loses half of its velocity after penetrating 36 cm. Further distance covered by it before coming to rest will be |
|
Answer» 18 cm `:.`During retarded MOTION. `x_1:x_2=3:1implies(x_1)/(x_2)=(3)/(1)impliesx_2(36)/(3)=12cm` |
|
| 6219. |
Two bodies begin to fal from the same height.The second body begins to fall 'tau' s after the first.After what time from the beginning of first body dose the distance between the bodies equals to l? |
|
Answer» Solution :Let the time of fall of the 1ST body be t seconds. Time of fall of SECOND body=`t-tau`. Distances of free fall of the bodies in the above time intervals RESPECTIVELY are `H_(1)=("gt"^(2))/(2),H_(2)=(g(t-tau)^(2))/(2)` Therefore `L=H_(1)-H_(2)="gt"tau-(1)/(2)gtau^(2) thereforet=(l)/("gt"au)+(tau)/(2)` |
|
| 6220. |
A metebridge is used to determine the resistance of an unknown wire by measuring the balance point length l. If the wire is replaced by another wire of same material but with double the length and half the thickness the balancing point is expected to be |
| Answer» Answer :C | |
| 6221. |
A particle of mass 1 mg has the same wavelength as an electron moving with a velocity of 3xx10^(6)ms^(-1). The velocity of the particle is (mass of electron =9.1xx10^(-31)kg) |
|
Answer» `2.7xx10^(-21)ms^(-1)` `implies v=(m_(e)v_(e))/(m)=((9.1xx10^(-31)kg)(3xx10^(6)ms^(-1)))/((1MG))=(9.1xx10^(-31)xx3xx10^(6))/(1xx10^(-6))=2.7xx10^(-18)ms^(-1)`. |
|
| 6222. |
A ray of light undergoes refraction when it enters from air to glass. A picture is painted with blue, green and red colours. A glass slab is placed on this picture. Will the imagesof all these colours lies in the same plane in the slab when viewed from the top of the glass ? Why ? |
| Answer» SOLUTION :No, DUE to REFRACTION. | |
| 6223. |
A long one- layer solenoid tightly would of wire with resistivity rho has n turns per unit length. The thickness of the wire insulation is negligible. The cross- sectional radius of the solenoid is equal to a. Find the phase difference betweencurrent and alternating voltagefed to the solenoid with frequency v. |
|
Answer» Solution :The current lags behind the voltage by the phase angle `varphi=tan^(-1)((omegaL)/( R))` Now `L=mu_(0)n^(2) pi a^(2)l, l=` LENGTH of the solenoid `R=(rho. 2PI a n .l)/( pi b^(2)), 2B=`diameter of the wire But `2 b n =1 :. B=(1)/(2n)` Then `varphi=tan^(-1)((mu_(0)n^(2)l pi a^(2). 2piv)/( rho. 2pi a n l ))xxpi(1)/( 4n^(2))` `=tan^(-1)((mu_(0)pi^(2) a v)/(4 rhon))` |
|
| 6224. |
Find the force experienced by a chloride ion having 4 electrons remover, when laced in an electric field of intensity 2 NC^(-1) |
|
Answer» SOLUTION :The force experienced by CHLORIDE ION is `F=qE = +(4 xx 1.6 xx10^(-19)) xx(2)` ` = +12.8 xx 10^(-19) N.` |
|
| 6225. |
The energy of H-atom in its ground state is -13.6 eV. Find the energy for energy levels having quantum number as 5. |
|
Answer» `E=-(13.6)/(N^(2))eV` For `n=5, E=-(13.6)/(5^(2))=-(13.6)/(25)=-0.54` eV. |
|
| 6226. |
When light falls on a metal surface, the maximum kinetic energy of the emitted photoelectrons depends upon : |
|
Answer» The time for which LIGHT falls on the metal |
|
| 6227. |
A chock coil has negligible resistance. The alternating p.d. across it, is 220V and the current is 5 mA. The power consumed is ……. |
|
Answer» <P>`220xx5/1000` W `delta=pi/2`, `P=(V_mI_m)/2 "cos" pi/2=0 "" [because "cos" pi/2=0]` |
|
| 6228. |
Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C_1 and C_2 with their capacitances in the ratio 1 : 2 so that the energy stored in the two cases becomes the same. |
|
Answer» Solution :Let `C_1 = C`, then as per QUESTION `C_2 = 2C_1=2C` In SERIES COMBINATION EQUIVALENT capacitance `C_s = (C_1 C_2)/(C_1 +C_2) = (Cxx 2C)/(C + 2C) = (2C)/3 ` and in PARALLEL differences applied across the series and parallel combinations be `V_s and V_p` respectively such that the energy stored in the two cases are same i.e., `u_s = u_p`. Since `u = 1/2 CV^2`. `:. 1/ 2 C_s V_s^2 = 1/2 C_pV_p^2` `rArr V_s/V_p = sqrt(C_p/C_s) = sqrt((3C)/((2C)/3)) = 3/sqrt2 rArr V_s : V_p = 3 : sqrt2` |
|
| 6229. |
Statement-I : sound waves of frequency less than 20Hz is not audiable to human beings. Statement-II : infra sonic waves are produced during earthquakes. |
|
Answer» STATEMENT -I is true, Statement -II is true and |
|
| 6230. |
(A) : A portable AM radio set must be kept horizontal to receive the signals properly. (R) : Radio waves are polarised electromagnetic waves. |
|
Answer» Both 'A' and 'R' are TRUE and 'R' is the CORRECT EXPLANATION of 'A'. |
|
| 6231. |
Iron (z = 26) emits k_(alpha) line of wavelength 1.96A^(@). For an element of unknown atomic number the wavelength of k_(alpha) line is 0.49A^(0) The atomic number of the unknown element is |
|
Answer» 51 |
|
| 6232. |
A convex lens is in contact with a concave lens. The magnitude of the ratio of their focal lengths is (2)/(3). Their equivalent focal length is 30 cm. What are their individual focal lengths? |
|
Answer» `-75CM, 50cm` As `(1)/(f)=(1)/(f)+(1)/(f_(2))`, hence `(1)/(30)=(1)/(f_(1))+(1)/((-(3)/(2)f_(1)))=(1)/(f_(1))-(2)/(3f_(1))=(1)/(3f_(1))RARR f_(1)=10 cm and f_(2)=-15cm`. |
|
| 6233. |
in the above given three particle system if two particles are kept fixed and third particle is relased Then speed of the particle when it reaches to the mid-point of the side connecting other two masses . |
|
Answer» `SQRT((2Gm)/(a))` |
|
| 6234. |
According to Bohr's theory the possible value of angular momentum of an electron orbiting in hydrogen atom is |
| Answer» Answer :B | |
| 6235. |
If n_i, n_e and n_h represents the number of intrinsic charge carrier, number of free electrons and number of holes respectively in semiconductor, then relation n_h n_e=n_i^2 is true for |
|
Answer» INTRINSIC semiconductor |
|
| 6236. |
Pick out the longest wavelength from the following types of radiations |
|
Answer» BLUE LIGHT |
|
| 6237. |
किसी माध्यम की आपेक्षिक परावैद्युता (relative permittivity) epsilon_r बराबर होती है, जहाँ epsilon माध्यम की निरपेक्ष परावैद्युता (absolute permittivity) तथा epsilon_0 मुक्त आकाश (free space) की परावैदयुता है । |
|
Answer» `epsilon/epsilon_0` |
|
| 6238. |
In an n-type silicon, which of the following statement is true. |
|
Answer» Electrons are MAJORITY carriers and TRIVALENT at- OMS are the dopants. |
|
| 6239. |
A storage battery of emf 80V and internal resistance 0.5Omega is being charged by a 120 V dc supply using a series resistor of 15.5Omega. What is the terminal voltage of the battery during charging ? What is the purpose of having a series resistor in the charging circuit ? |
| Answer» Solution :81.25 V, the series resistor LIMITS the CURRENT DRAWN from the external source. In its absence, the current will be dangerously high | |
| 6240. |
Find the angle between two plane mirrors such that a ray of light incident on the first mirror and parallel to the second mirror is reflected from the second mirror, parallel to the first mirror. |
|
Answer» SOLUTION :In TRIANGLE BOC, we have `3 theta=180^@` `theta=60^@` |
|
| 6241. |
A magnet NS is suspended from a spring and while oscillates, the magnet moves in and out of the coil C. The coil is connected to a galvanometer G. Then as the magnet oscillates |
|
Answer» G shows deflection to the LEFT and RIGHT with constant AMPLITUDE |
|
| 6242. |
If a p-n junction diode is not connected to any circuit, |
|
Answer» the potential is the same everywhere |
|
| 6243. |
माना R वास्तविक संख्याओ का समुच्चय है तथा f:RrarrR एक फलन |
|
Answer» एकैकी |
|
| 6244. |
A particle of mass m = 0.1 kg and having positive charge q = 75 mu C is suspended from a point by a thread of length l = 10 cm. In the space, a uniform horizontal electric field E = 10^4 NC^-1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g = 10 ms^-2). |
Answer» SOLUTION :Weight mg of the particle acts vertically downward and force q E horizontally. Therefore, in equilibrium position, the thread is inclined to the vertical. Let, in static equilibrium of the particle, inclination of the thread with the vertical be q and tension be `T_0`.  . . Considering free body diagram, `T_0 sin theta = q E and T_0 cos theta = q E` `rArr tan theta = (q E)/(mg) or theta = 37^(@)` The particle moves along a circle with costant speed. This possible only when the thread traces the surface of a cone whose AXIS is inclined at an angle `theta` with the vertical. This arrangement is now called conical pendulum. Note: The axis a conical perndulum is always along the thread when the particle is in stanic equilibrium position. Horozontal velocity impared to the particle must be perpendicular to the direction of electric FIELD. Radius of circular path is `r = l sin theta = 6 cm`. Now considering free body diagram of the revolving particle and resolving the forces NORMAL to the direction of resultant force (centripetal force), `T cos theta = mg cos theta + qE sin theta` =`1.5625 N` Now resolving the forces along the direction of resultant force, `qE cos theta + T sin theta - mg sin theta = (m v^2)/(r)` or `v = 0.75 ms^-1`. |
|
| 6245. |
Unpolarised light of intensity 32 watt m^(-2) passes through three polarises such that the transmission axes of the first and second polarises makes an angle 30^(@) with each others the transmission axes of the second and third polarises makes an angle 60^(@) with each other. The intensity of final emerging light will |
|
Answer» 32 watt `m^(-2)` `I=(I_(0))/(2)cos^(2)30^(@)""cos^(2)60^(@)=3` watt `m^(-2)` |
|
| 6246. |
The equation of a projectile is y=sqrt(3)x-g/2x^(2) the angle of its projection is : |
|
Answer» `THETA=tan^(-1)1/sqrt(3)` `X=ucosthetaxxt or t=x/(ucostheta)` `y=ucostheta.x/(ucostheta)-1/2gxxx^(2)/(U^(2)cos^(2)theta)` `=x.tantheta-1/2(GX^(2))/(u^(2)cos^(2)theta)` compairing with given equation `y-sqrt(3)x-(gx^(2))/2` we have `tantheta=sqrt(3)` or `theta=tan^(-1)sqrt(3)` |
|
| 6247. |
Assertion : When a particle moves in a circle with a uniform speed its acceleration is constant but the velocity changes. Reason : Angular displacement is not a axial vector. |
|
Answer» Both ASSERTION & REASON are TRUE & the Reason is a CORRECT EXPLANATION of the Assertion. |
|
| 6248. |
Who is credited with the discovery of photon? |
|
Answer» Chadwick |
|
| 6249. |
A tuning fork A produces 4 beats with tuningfork B of frequency 256 Hz. When A is filed beats are found to occur at shorter intervals. What was its original frequency? |
|
Answer» SOLUTION :As tuning fork Aproduces 4 beats with B of FREQUENCY `(f_B =256 Hz)`, the frequency of A, `f_A` will be `f_A = f_b pm 4 = 256 pm 4, i.e., f_A =252 Hz or 260 Hz` Now on filing due to decrease in inertia frequency of A will increase and occurrence of beats at shorter duration means increase in BEAT frequency, so if `f_A= 252 Hz, 256 - f_A = 4Hz` and so with increase in `f_A` beat frequency will decrease. If `f_A =260 Hz, f_A -256 = 4 Hz`and so with increase in `f_A` beat frequency will increase and as on filing frequency increases. `:.` The frequency of A before filing was 260 Hz |
|
| 6250. |
The energy of an electron in an excited hydrogen atom is -3.4eV. The angular momentum of electron, according to Bohr's theory is |
|
Answer» `(H)/(2PI)` |
|