Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 6101. |
A plane of thickness t madeof a materialof refractiveindex mu ispalced is frontof one of the slits ina doubleslitexperiment(a) . Findthe changein the optical path dueto introduction of the plate (b) Whatshouldbe the minimumthickness t whichmakethe intensityat the centre of the fringe patternzero ? Wavelength of the light used is lambda.Neglect any absorption of light in the palne . |
|
Answer» `(mu-1)t, LAMBDA/(2(mu-1))` |
|
| 6102. |
(a) In Fig. 32-19a, a beam of monochromatic light reflects and refracts at point A on the interface between material 1 with index of refraction n_(1)= 1.33 and material 2 with index of refractionn_(2) =1.77. The incident beam makes an angle of 50^(@)) with the interface. What is the angle of reflection at poinl A ? What is the angle of refraction there? |
|
Answer» Solution : (1) The angle of reflection is equal to the angle of incidence, and both angles are measured relative to the normal to the surface at the point of reflection. (2) When light reaches the interface between two materials with different INDEXES of refraction ( call them `n_(1)` and `n_(2)` ), part of the light can be refracted by the interface according to Snell.s law, Eq. 33-35: `n_(2) sin theta_(2) =n_(1) sin theta_(1)` where both angles are measured relative to the normal at the point of refraction. Calculations: In Fig. 32-19a, the normal at point A is drawn as a dashed line through the point. Note that the angle 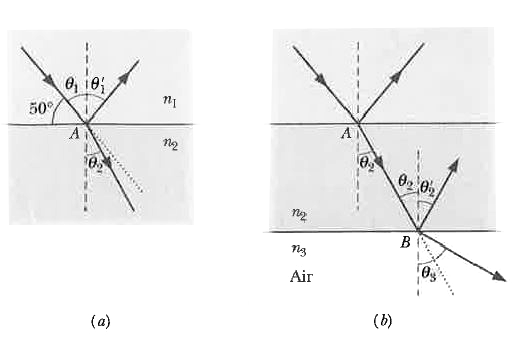 of incidence `theta` , is not the given `50^(@)`but is `90^(@)-50^(@) = 40^(@)`. Thus, the angle of reflection is `theta_(1) = theta_(1) = 40^(@)` . The light that passes from material 1 into material 2 undergoes refraction at point A on the interface between the two materials. Again we measure angles between light rays and a normal, here at the point of refraction. Thus, in Fig. 32-19a, the angle of refraction is the angle marked `theta_(2)`Solving Eq. 32-37 for `theta_(2)` , GIVES us `theta_(2) = sin^(-1) ((n_(1))/(n_(2))sintheta_(1))=sin^(-1)((1.33)/(1.77)sin 40^(@))` `=28.88^(@)~~29^(@)` . This result means that the beam swings toward the normal (it was at `40^(@)` to the normal and is now at `29^(@)`.) The reason is that when the light travels across the inter face, it moves into a material with a greater index of refraction. Caution: Note that the beam does not swing through the normal so that it appears on the left side of Fig. 32-194. (b) The light that enters material 2 at point A then reaches point B on the interface between material 2 and material 3, which is air, as shown in Fig. 32-19b. The interface through B is parallel to that through A. At B, some of the light reflects and the rest enters the air. What is the angle of reflection? What is the angle of refraction into the air? Calculations: We first need to relate one of the angles at point B with a known angle at point A. Because the ntertace through point B IS parallel to that through point A, the incident angle at B must be equal to the angle of refraction `theta_(2)`as shown in Fig. 32-19b. Then for reflection we again use the law of reflection. Thus, the angle of reflection at B is `theta_(2) = theta_(2) = 28.88^(@)~~29^(@)` . NEXT, the light that passes from material 2 into the air undergoes refraction at POINTB, with refraction angle `theta_(3)`Thus, we again apply Snell.s law of refraction, but this time we write Eq. 32-35 as `n_(3) sin theta_(3) =n_(2) sin theta_(2)`. Solving for `theta_(3)` then leads to `theta_(3) =sin^(-1)((n_(2))/(n_(3))sintheta_(2))=sin^(-1)((1.77)/(1.00)sin28.88^(@))` `=58.75^(@)~~59^(@)`. Thus, the beam swings away from the normal (it was at `29^(@)`to the normal and is now at `59^(@)`) because it moves into a material (air) with a lower index of refraction |
|
| 6103. |
A large drop of mercury of radius 1.0 mm splits into 1000 small droplets. If S.T. of mercury is 500 dyne/cm, the amount of energy |
|
Answer» `180 piergs` is released |
|
| 6104. |
A railway carriage has it's C.G at a height of 1 m above the rail which are also 1 m apart. The maximum safe speed at which it can travel round unbaked curve of radius 80m is |
|
Answer» 1.98 m/s |
|
| 6105. |
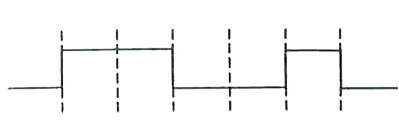
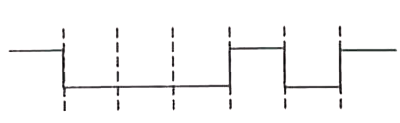
The logic circuit shown below has the input waveform 'A' and 'B' as shown . Pick out the correct output waveform . output is : |
|
Answer»
ACCORDING to Demorgan.s THEOREM, `Y = bar(A).bar(B) = A.B` |
|
| 6106. |
A small ball of conducting material having a charge +q and mass m is thrown upward at and angle theta to horizontal surface with an initial speed nu_(0) as shown in the figure. There exists an uniform electric field E downward along with the gravitational field g . Calculate the range maximum height and time of flight in the motion of this charged ball. Neglect the effect of air and treat the ball as a point mass . |
|
Answer» Solution :If the conductor has no net CHARGE then its motion is the same as usual projectile motion of a mass m . Here in this problem in additionto downward gravitational force the charge also will experience a downward uniform electronstatic force. The acceleration of the charged ball due to gravity =-g `HATJ` The acceleration of the chargedball due to uniform ELECTRIC field = `-(qE)/(m)hatj` The total acceleration of charged ball in downward direction `vec=-(g+(qE)/(m))hati` It is important here to note that the acceleration depends on the mass of the OBJECT . Galileo conclusion that all objects fall at the same rate towards the Earth is true only in a unifrorm gravitational field . When a uniform electric field is included the acceleration of a charged object depends on both mass and charge . But still the acceleration a = `(g+(qE)/(m))` is constant through the motion. Hence we use kinematic equations to calculate the range maximum height and time of flight. In fact we can simply replace g by `g+(qE)/(m)` in the usual expressions of range maximum height and time of flight of a projectile .  Note that the time of flight maximum height range are all inverselyproprotional to the acceleration of object . Since `(g+(qE)/(m)) gt g` y for charge +q the quantities T, `h_("max")` and R will decrease when compared to the motion of an object of mass m and zero net charged. Suppose the charges is then `(g-(qE)/(m))lt g ` and the quantities T `h_("max")` and R will increase . Interestingly the trajectory is still parabolic as shown in the FIGURE . 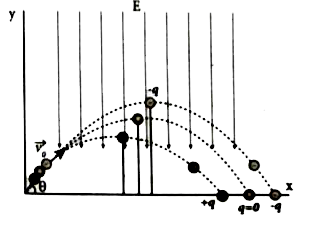
|
|
| 6107. |
Due to which phenomenon, the colour of sky seems to be blue ? |
|
Answer» REFLECTION |
|
| 6108. |
A train is moving with a uniform speed of 33 m/s and an observer is approaching the train with the same speed. If the train blows a whistle of frequency 1000 Hz and the velocity of sound is 333 m/s, then the apparent frequency of the sound that the observer hears is |
|
Answer» 1220 HZ `u =((v+v_(0))/(v-v_(0)))v_(0)` Here, `v_(0) = 1000 Hz, v_(0) = v_(s) = 33 MS^(-1)` `v = 333 ms^(-1), v=?` `v=((333 + 33)/(333-33)) xx 1000 = 366/300 xx 1000 = 1200` Hz |
|
| 6109. |
A 0.5kg block slides from the point A on a horizontal track with an initial speed 3 m//s towards a weightless horizontal spring of length 1m and force constant 2N//m. The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as '0.22' and0.20 respectively. If the distances AB and BD are 2m and 2.14m respectively, find total distance through which the block moves before it comes to rest completely. (g=10 m//s^(2) ). |
|
Answer» point north - WEST |
|
| 6110. |
What are the reasons to believe that light is a wave motion ? |
| Answer» Solution :LIGHT undergoes INTERFERENCE, diffraction and polarisation. These phenomena ESTABLISH that light is a wave MOTION. | |
| 6111. |
One of the surfaces of a biconvex lens of focal length 10 cm is silvered as shown in figure. Radiusof curvature of silvered surface is 10 cm. At a given instant, if speed of object is 1 m/s, then the speed of image at that instant is (10 +alpha) m/s. What will be the value of alpha ? (mu =1.5) |
|
Answer» |
|
| 6112. |
In Fig. 27-38, two batteries with an emf epsi= 12.0 V and an internal resistance r=0.500 Omega are connected in parallel across a resistance R. (a) For what value of R is the dissipation rate in the resistor a maximum? (b) What is that maximum? and (c) what is the total dissipation rate in the batteries? In terms of r, what are (d) the effective R (internal) resistance of the two-battery system and (e) the resistance R that is required to maximize the dissipation rate? This is a general result. |
|
Answer» |
|
| 6113. |
For the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s How long does it take for the mechanical energy to drop to one-half its initial value? |
|
Answer» Solution :From Eq. 15.35 the mechanical energy at time t is `1//2kx_(m)^(2) e^(-bt//m)` Calculations: The mechanical energy has the value `1//2kx_(m)^(2)` at t=0, Thus, we must find the value of t for which `(1)/(2) kx_(m)^(2) e^(-bt//m) = (1)/(2) ((1)/(2) kx_(m)^(2))`. If we divide both sides of this equation by `1//2kx_(m)^(2)` and solve for t as we did above, we find `t= (-m In (1)/(2))/(b) = (-(0.25kg) (In (1)/(2)))/(0.070kg//s) = 2.5s`. This is exactly half the time we calculated in (b), or about 7.5 periods of OSCILLATION. FIGURE 15.21 was drawn to ILLUSTRATE this sample problem. |
|
| 6114. |
In the given LC circuit,if initially capacitor C has charge Q on it and 2C has charge 2Q. The polar ar as shown in figure. Then after closing switch S and t=0 |
|
Answer» energy will get EQUALLY distributed in both the capacitors UST after closing the switch |
|
| 6115. |
When a bar magnet is placed at 90^(@) to a uniform magnetic field, it is acted upon by a couple which is maximum. For the couple to be half of the maximum value, at what angle should the magnet be inclined to the magnetic field (B)? |
|
Answer» SOLUTION :We know that , `TAU = MB sin theta ` If ` theta = 90^(@) " then " tau_("max")=MB`........... (1) From equation (1) and (2) `2 = (1) sin thetaor sin theta = (1)/(2) or theta = 30^(@)` |
|
| 6116. |
The contrast between the fringes in any interference pattern depends on |
|
Answer» FRINGE width |
|
| 6117. |
In Q.No. 6-9 |
|
Answer» Wave velocity is `(omega)/(K)` |
|
| 6118. |
Calculate the resultant capacitances for each of the following combinations of capacitors . |
Answer» Solution :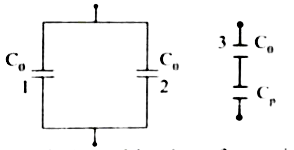 Parallel COMBINATION of capacitor 1 and 2 `C_(p)= C_(0)+C_(0)=2C_(0)` Series combination of capacitor `C_(p)` and 3 `(1)/(C_(s))=(1)/(C_(p))+(1)/(C_(3))=(1)/(2C_(0))+(1)/(C_(0))" (or)" (1)/(C_(s))=(3)/(2)C_(0)" " "(or)" " "C_(s)=(2)/(3) C_(0)` (b) 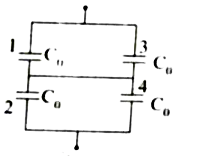 Capacitor 1 and 2 are series combination `(1)/(C_(s_(1)))=(1)/(C_(1))+(1)/(C_(2))=(1)/(C_(0))+(1)/(C_(0))=(1)/(C_(0))" (or)" (1)/(C_(s_(1)))=(2)/(C_(0))"(or)" C_(s_(1))=(C_(0))/(2)` Similarly 3 and 4 are series combination `(1)/(C_(s_(1)))=(1)/(C_(3))+(1)/(C_(4))+(1)/(C_(0))+(1)/(C_(0))=(2)/(C_(0)) "(or)" C_(s_(2))=(C_(0))/(2)` `C_(s_(1)) ` and `C_(s_(2))` are in parallel combination 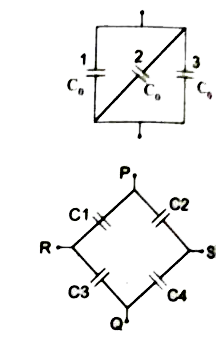 `C_(P)= C_(s_(1))+C_(s_(2))=(C_(0))/(2)+(C_(0))/(2) "(or)" C_(P)= (2C_(0))/(2) "" C_(P)=C_(0)` (c ) Capacitor 1,2 and 3 are in parallel combination `C_(P)=C_(0)+C_(0)+C_(0)=3C_(0)` `C_(P)=3C_(0)` (d) Capacitar `C_(1)` and `C_(2)` are in combination `(1)/(C_(s_(1)))=(C_(1)+C_(2))/(C_(1)C_(2))` `C_(s_(1))= (C_(1)C_(2))/(C_(1)+C_(2))` 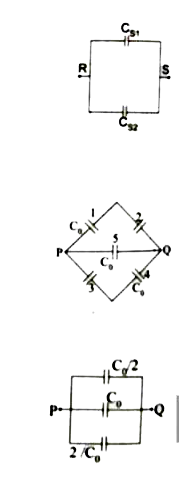 Similarly `C_(3)` and `C_(4)` are in series combination `(1)/(C_(s_(2)))=(1)/(C_(3))+(1)/(C_(4))=(C_(3)+C_(4))/(C_(3)C_(4))` `C_(s_(2))= (C_(3)C_(4))/(C_(3)+C_(4))` `C_(s_(1)) ` and `C_(s_(2))` are in parallel combination ACROSS R.S: `CP = C_(s_(1))+ C_(s_(2))` `=(C_(1)C_(2))/(C_(1)+C_(2))+(C_(3)C_(4))/(C_(3)+C_(4))=(C_(1)C_(2)(C_(3)+C_(4))+C_(3)C_(4)(C_(1)+C_(2)))/((C_(1)+C_(2))(C_(3)+C_(4)))` `C_(P)=(C_(1)C_(2)C_(3)+C_(1)C_(2)C_(4)+C_(3)C_(4)C_(1)+C_(3)C_(4)C_(2))/((C_(1)+C_(2))(C_(3)+C_(4)))` (e) Capacitor 1 and 2 are series combination `(1)/(C_(s_(1)))=(1)/(C_(1))+(1)/(C_(2))=(1)/(C_(0))+(1)/(C_(0))=(1)/(C_(0))` `(1)/(C_(s_(1)))=(2)/(C_(0)) "(or)" C_(s_(1)) = (C_(0))/(2)` Similarly 3 and 4 are series combination `(1)/(C_(s_(2))=(2)/(C_(0)) "(or)" C_(s_(2))= (C_(0))/(2)` Three CAPACITORS are in parallel combination |
|
| 6119. |
Assertion (A) : Eventhough forward bias is known to be more (mA) than the current in the reverse bias (mu A), photodiodes are still used in reverse bias. Reason ( R) : The fractional change in majority charge carriers woulb be much less than that in minority charge carriers due to photo-effects so that minority carrier reverse bias current is more easily to measure with photo diodes than majority carrier forward current. |
|
Answer» |
|
| 6120. |
A mixture of light, consisting of wavelength 590 nm and an unknown wavelength, illuminates Young's double-slit and gives rise to two overlapping interference patterns on the screen. The central maximum of both lights coincide. Further, it is observed that the third bright fringe of known light concides with the 4th bright fringe of the unknown light. from this data, the wavelength of the unknown light is |
|
Answer» 885.0 nm `THEREFORE lamda.=(3)/(4)lamda=(3)/(4)xx590nm=442.5nm`. |
|
| 6121. |
A body of mass 1 kg is rotating in a verticle circle of radius 1 m .What will be the difference in its kinetic energy at the top and bottom of the circle ? (g=10m//s^(2)) |
|
Answer» 10 J |
|
| 6122. |
Two bodies are thrown form the same pointwith the same velocity of projection , angles of projected 30^(@) and 60^(@). If R_(1) and R_(2)are the ranges and h_(1)andh_(2)are maximum height respectively , then find the relationsamong them. |
| Answer» Solution :`R_(1) = R_(2) = (U^(2))/(G),h_(1) + h_(2) = (u^(2))/(2G)` | |
| 6123. |
According to Curie's law ..... |
|
Answer» `chi_(m) prop T` `THEREFORE chi_(m) prop (1)/(T)(mu_0 and C` are constant `)` |
|
| 6124. |
If a flywheel of mass 20 kg and diameter 1 m is rotation at 300 rpm.What is its kinetic energy? |
|
Answer» 1234 J |
|
| 6125. |
Two identical charged spheres suspended from a common point by two masses strings of length l are initially at a distance d (d lt lt 1) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate. As a result the charge approaches each other with a velocity v. Then as a function of distancex between them |
|
Answer» `V prop x^(-1)` `F = T sin theta` Weight of each sphere = `MG = T cos theta` `:. Tan theta = F/(mg) or x/(2l) = (1/(4PI epsilon_0)(q^2)/(x^2))/(mg) or (x^3)/(2l) = 1/(4 pi epsilon_0) cdot (q^2)/(mg)` `or q prop^(3//2)` 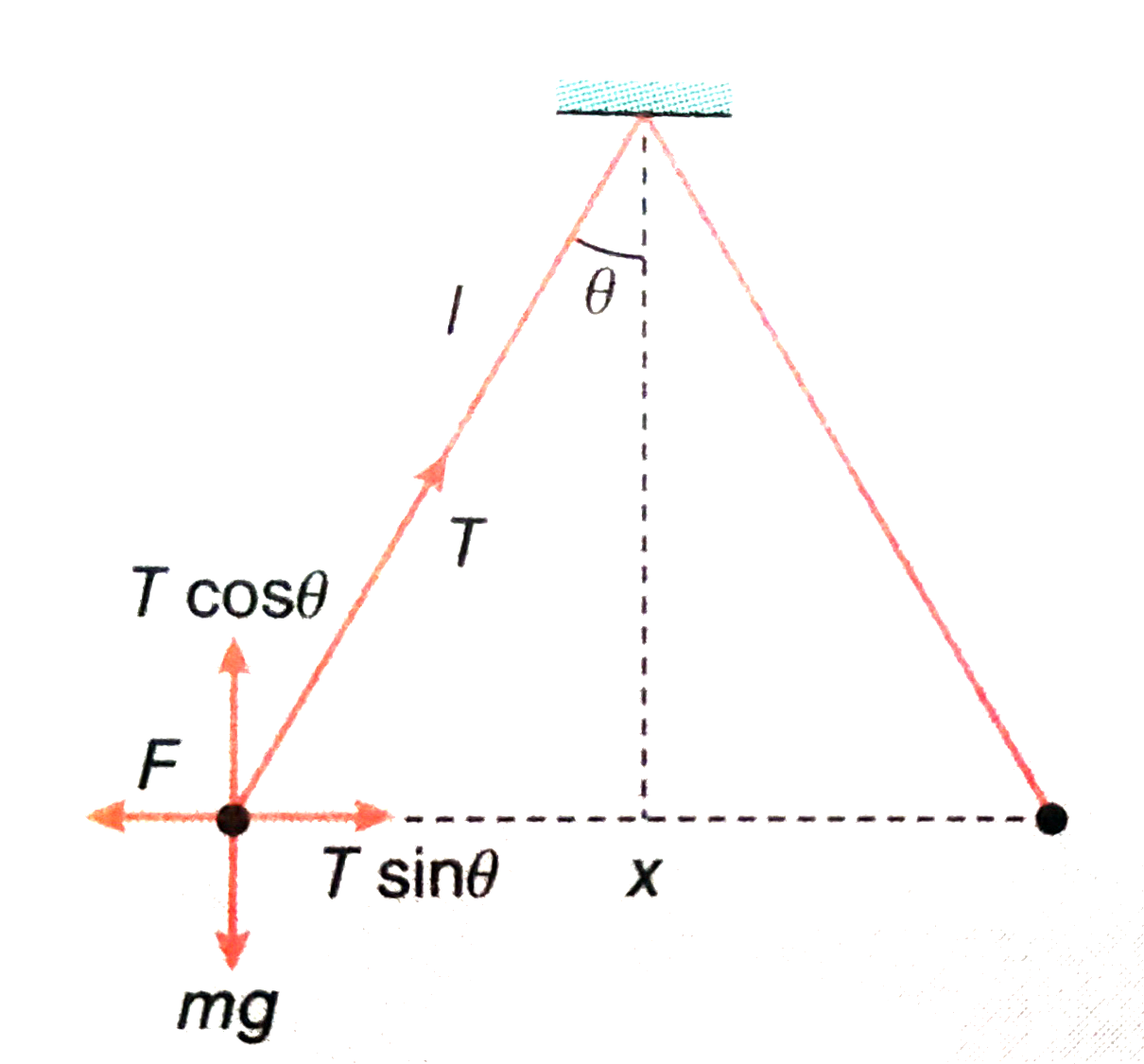 Difference with respect to t, `(dq)/(dt) prop 3/2 x^(1/2) (DX)/(dt) or, v prop x^(-1/2) [ :' (dq)/(dt)` = constant]. |
|
| 6126. |
A man of 55 kg is holding a bucket of mass 25 kg. He walks 50 m on a level road at a constant speed of 3 ms" and then climbs up a hill of height 20 m. What is the work done by the man ? |
|
Answer» 16 KJ `:.` work is done in climbing the hill. `W=(M+m)gh=(55+25)xx10xx20=16000 J` = 16 J |
|
| 6127. |
In a solid, oxide ions are arranged in ccp, cations 'A' occupy one sixth of tertrahedral voids and cations 'B' occupy one third of the octaherdral voids .Which of the following is the correct formula of the oxide? |
|
Answer» `ABO_(3)` Cation `B = 1/3xx4=4/3` `O^(2-)=8xx1/8+6xx1/2=4` `A:B:O^(2-)=4/3:4/3:4=1:1:3` |
|
| 6128. |
What are dimensions of electrical conductivity ? |
|
Answer» SOLUTION :The reciprocal of RESISTIVITY `(rho)` is called electrical conductivity `(SIGMA)` i.e. `sigma=1/rho,sigma=1/rho=(n e^2tau)/m=(L^(-3)(AT)^(-2)XXT)/M` `M^(-1)L^(-3)T^3A^2` |
|
| 6129. |
Charges of upquark and downquark are ...... and......respectively. |
|
Answer» `-2/3e, -1/3 E` |
|
| 6130. |
Thegravitational forceon a bodyof mass1.5kg situatedat a pointis 45 M . The gravitationalfield intensityat thatpoint is . |
|
Answer» Potentialenergywill INCREASE |
|
| 6131. |
The length of potentiometer wire is 1m and its resistance is 4 Omega .A current of 5mA is flowing in it. An unknown emf is balanced on 40cm length of this wire. The unknown emf is |
|
Answer» 8v |
|
| 6132. |
Mention any three properties of diamagnetic substance. |
|
Answer» Solution :The properties of diamagnetic are These substances which have tendency to move, from stronger to the weaker region of the EXTERNAL magnetic field. OR these substances which are weakly repelled by the magnetic field. Their magnetic susceptibility `(chi)` is small and negative VALUE `(- 1 lt chi lt 0)` Their relative permeability is less than one `(0 lt mu_(R ) lt 1)` Their permeability is less than absolute permeability `(mu lt mu_(0))` Their susceptibility `(chi)` is independent of TEMPERATURE. |
|
| 6133. |
Two balls are dropped from heights h and 2h respectively. The ratio of time taken by these balls to reach the earth is |
|
Answer» `1: sqrt(2)` Here a= G , Initial velocity ` u= 0 , s_(1) = (1)/(2) "gt"_(1)^(2), s_(2)=(1)/(2)"gt"_(2)^(2)` `(s_(1))/(s_(2))=(t_(1)^(2))/(t_(2)^(2)) :. (t_(1))/(t_(2))= sqrt(s_(1)/s_(2))=sqrt((H)/(2h))=(1)/(sqrt(2))` |
|
| 6134. |
A body is kept moving with uniform speed in a circle by a centripetal force acting on it. However the work done by this force is zero. Is it true ? Explain.. |
| Answer» Solution :WORK done by a force `W=Fs cos theta`. As centripetal force is ALWAYS at right angles to DISPLACEMENT `cos theta =cos 90=0`.HENCE, work done is ZERO. | |
| 6135. |
Select the correct statement (s) from the following |
|
Answer» A fusion reactor requires a very high temperature , of the ORDER of `10^(7)` K , while a fission reactor does not require such high temperatures . |
|
| 6136. |
a. Determine the 'effective focl length ' of the combination of the two lenses in Exercise 9.10, if they are placed 8.0 cm apart with their principal axes coincident . Does the answer depend on which side of the combination a beam of parallel lightis incident? in the notion of effective focal length of this system useful at all ? |
|
Answer» 0.98 cm |
|
| 6137. |
Locomotory organs not found in protozoans are |
|
Answer» parapodia |
|
| 6138. |
Two long parallel wires separated by a distance r, carries equal current I exert a force F per unit length. The distance r is reduced to r/2 and the current in each wire is I/4. Now the force between them is |
|
Answer» `F/8` |
|
| 6139. |
A metal rod of resistance 20Omegais fixed along a diameter of a conducting ring of radius 0.1m and lies on x-y plane. There is a magnetic field vecB = (50T)hatk. The ring rotates with an angular velocity omega= 20rad /s about its axis. An external resistance of 10Omegais connected across the centre of the ring and rim. The current through external resistance is |
Answer» Solution : `e = 1/2 Bl^2 omega = 1/2 xx 50 xx 0.1 xx 0.1 xx 20` ` therefore e = 5V` HENCE the current through the external RESISTANCE is `i = e/R therefore i = 5/15 = 1/3 `AMP 
|
|
| 6140. |
If the distance between two point particles is doubled, then the gravitational force between them |
|
Answer» decreases by a FACTOR of 4 |
|
| 6141. |
A vertical capillary of radius r is brought in constant with water of density rho and surface tension S. If the angle of contact is zero, then the amount of heat liberated while the water rises along the capillary, is |
|
Answer» `(2PI S^(2))/(rhog)` |
|
| 6142. |
If .b. represents the size of object interacting with Light L representsthe distance betweenobject and screen , X is the wavelength of light then , matchthe followinglists: |
|
Answer» |
|
| 6143. |
A square shaped plane coil of area 100 cm^(2) turns a carries a steady current of 5 A . It is placed in a uniform magnetic field of 0.2 T acting perpendicular to the plane of the coil. Calculate the torque on the coil when its when makes an angle of 60^@ with the direction of the field. In which orinetation will the coil be in stable equilibrium? |
|
Answer» Solution :Here area of coil `A = 100 cm^2 = 10^(-2) m^2, ` number of turns N = 200, current I = 5 A, MAGNETIC FIELD B = 0.2 T. As plane of coil makes an angle of `60^@` with the direction of the field hence angle between `vecA and VECB` is `theta = 90^@ - 60^@ = 30^@` `:.` Torque `tau = NA IB sin theta = 200 xx 10^(-2) xx 5 xx 0.2 xx sin 30^@ = 1 N-m` The coil will be in stable EQUILIBRIUM when plane of the coil is perpendicular to the direction of magnetic field B so that `vecA and vecB` are parallel and torque `tau = 0`. |
|
| 6144. |
Te magnetic induction field at the centroid or an equilateral triangle of side 'I' nnd canying a current 'i' is |
|
Answer» `(2sqrt2mu_(0)i)/(PIL)` |
|
| 6145. |
A cylindrical rod is having temperature T_(1) and T_(2) ate its ends. The rate of flow of heat is Q_(1) cal/sec. If all the linear dimensions are doubled keeping temperatures constant, then rate of flow of heat Q_(2) will be : |
|
Answer» `4Q_(1)` When linear DIAMENSION are doubled then A becomes 4 times and d becomes 2 times. `:.(dQ)/(dt)` becomes 2 times Correct choice is (c ). |
|
| 6146. |
The electric field at a distance (3R)/2 from the centre of a charged conducting spherical shell of radiu R is E. The electric field at a distance R/2 from the centre of the sphere is: |
|
Answer» zero |
|
| 6147. |
Consider the situation shown in figure. The two slits S_1 and S_2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength lamda. The separation between the slits is d. The light transmitted by the slits falls on a screen Sigma_1 placedat a distance D from the slits. The slit S_3 is at the placedcentral line and the slit S_4, is at a distance z from S_3. Another screenSigma_2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Sigma_2 if z is equal to a. z=(lamdaD)/(2d) b. (lamdaD)/d c. (lamdaD)/(4d) |
|
Answer» minimum intensilty OCCURS, (dark fringe) `RARR Amplitude =0` At `S_3` path differenc e=0` rarr maximum intensity occurs. rarr Amplitude =2r So on `Sigma^2` screen, `l_(max)/l_(min)=((2r+0)^2)/((2r-0)^2)=1` ii. When z=(lamdaD)/d ` As `S_4` maximum intensity occurs `rarr Amplitude =sqrt2r` At `S_3` also maximum intensity occurs. `l_(max)/l_(min)=((2r+2r)^2)/((2r-2r)^2)=oo` iii When `z=(lamdaD)/(4d), at S_4` intensity =l_(max)/2` `rarr Amplitude=sqrt2r` `:. At S_3` Intensilty is minimum `rarr Amplitude =2r `l_(max)/l_(min)=((2r+sqrt(2r))^2)/((2r-sqrt(2r))^2)=34` |
|
| 6148. |
Generally, we consider that during slowing of a moving automobile, its retardation is constant, but in practice this is seldom the case. Under many circumstances, especially at high speed, we usually apply the brakes slowly at first and then more strongly as the car slows. The braking force therefore depends on the time during the interval over which the car is slowing and acceleration changes with time. a_(x)(t)=(v_(A)-v_(x))/(dt) =(F_(x)(t))/(m) int_(v_(0_(x)))^(v_(x))dV_(x)=int_(0)^(1)(F_(x)(t))/(m)dt therefore V_(x)=V_(0x)+(1)/(m) int_(0)^(1)F_(x) (t) dt x(t)=x_(0)+int_(0)^(1) V_(x) (t) dt An example for the same is discussed here. A car of mass m = 1000 kg is moving with 25 m/s. The driver begins to apply the brakes so that the magnitude of the braking force increases linearly with time at a rate of 2000 N/s. Read the above passage carefully and answer the following questions. Find the velocity of the car at t= 10 sec. |
|
Answer» ZERO |
|
| 6149. |
A long charged cylinder of linear charge density lambda is surrounded by a hollow co-axial conducting cylinder. What is electric field in the space between the two cylinders? |
|
Answer» Solution :CHARGE density `=lambda`. The flux calculated for a cylinderical surface of RADIUS r, over a length l is E. `2PI rl`. By Gauss THEOREM, `E.2pi rl=(l lambda)/(epsi_(0))` `E=lambda/(2pi epsi_(0)) or vecE=(lambda)/(2pi epsi_(0)) hatn` 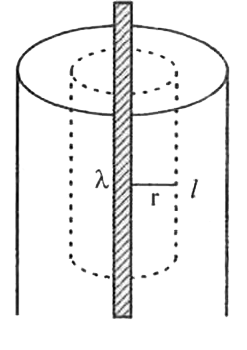
|
|
| 6150. |
If a disc slides from top to bottom of an inclined plane, it takes time t_(1). If it rolls, it takes time t_(2). Now, (t_(2)^(2))/(t_(1)^(2)) is |
|
Answer» `(1)/(2)` Also the rolling time `t_(2)=sqrt((3l)/(gsintheta))` `THEREFORE (t_(2)^(2))/(t_(1)^(2))=(3)/(2)` |
|