Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

37401.

The magentic field B at the centre O in fig. shown is

Answer»

`(mu_0I)/(4)[(1)/(R_1) - 1/(R_2)]`
`(mu_0I)/(4)[(1)/(R_1) + 1/(R_2)]`
`(mu_0I)/(4)(R_1 - R_2)`
`(mu_0I)/(4)(R_1 + R_2)`

ANSWER :B
Discussion
37402.

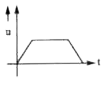
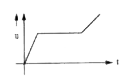
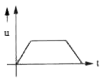
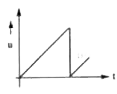
Figure shows the acceleration time graph of a particle. Which of the following represents the corresponding velocity-time graph ?

Answer»




ANSWER :B
Discussion
37403.

Choose the correct alternative from the clues given at the end of the each statement: In the ground state of .......... electrons are in stable equilibrium, while in .......... electrons always experience a net force. (Thomson’s model/ Rutherford’s model.)

Answer»

SOLUTION :THOMSON’s MODEL, RUTHERFORD’s model
Discussion
37404.

A 20 a.m.u. atom emits photon of 6.6Å while making a transition from excited state to ground state. The recoil energy of the atom will be :

Answer»

<P>`1.5xx10^(-23)J`
`3.5xx10^(-23)J`
`5.1xx10^(-23)J`
`7.5xx10^(-23)J`

Solution :`:.p=(H)/(LAMBDA)`
Discussion
37405.

A parallel plate capacitor is to be designed with a voltage rating 1kV, using a maeterial of dielectric constant 3 and dielectric strength about 10^(7) Vm^(-1), (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i.e, without starting to conduct electricity through partial ionisation.) For safety, we should like the field never to exceed say 10% of the dielectric strength. What minimum area of the plates is required to have a capacitance of 50pF?

Answer»

Solution :`V=10^(3)V, epsi_(r)=3, ""E_(de)=10^(7)VM^(-1),""E=(10)/(100) xx 10^(7) =10^(6)Vm^(-1)`
`A=? C=50pF =50 xx 10^(-12)F`
`E=V/d, therefore d=V/E=(10^(3))/(10^(6))=10^(-3)m`
`C=(epsi_(0)epsi_(r)A)/(d)`
`A=(C.d)/(epsi_(0) epsi_(r))= (50 xx 10^(-12) xx 10^(-3))/(8.85 xx 10^(-12) xx 3)=1.9 xx 10^(-3) m^(2)=19 xx 10^(-4) m^(2)=19CM^(2)`
Discussion
37406.

Obtain Einstein's photoelectric equation with necessary explanation.

Answer»

Solution :When a photon of energy HV is incident on a metal surface, it is completely absorbed by a single electron and the electron is ejected.
In this process, a part of the photon energy is used for the EJECTION of the electrons from the metal surface (PHOTOELECTRIC work function `phi_(0)`) and the remaining energy as the kinetic energy of the ejected electron. From the law of conservation of energy.
`h upsilon = phi_(0) + (1)/(2) mv^(2)""...(1)`
where m is the mass of the electron and `upsilon` its velocity

If we reduce the frequency of the incident light, the speed or kinetic energy of photo electrons is also reduced. At some frequency `v_(0)` of incident radiation, the photo electrons are ejected with almost zero kinetic energy. Then the equation (1) becomes
`h upsilon_(0) = phi_(0)`
where `v_(0)` is the THRESHOLD frequency. By rewriting the equation (1), we get
`h upsilon = h upsilon_(0) + (1)/(2) mv^(2)""...(2)`
The equation (2) is known as Einstein.s Photoelectric equation.
If the electron does not lose energy by internal collisions, then it is emitted with maximum kinetic energy `K_(max)`. Then
`K_(max) = (1)/(2) mv_(max)^(2)`
where `upsilon_(max)` is the maximum velocity of the electron ejected. The equation (1) is rearranged as follows :
`K_(max) = h upsilon - phi_(0)`
Discussion
37407.

A uniform rod of mass M and lengthL is suspended in vertical position as shown in figure. A uniform horizontal electric field of strength E is present in the region. The rod undergoes small oscillation for different cases. Select correct statement (s)

Answer»

if a POINT CHANGE `Q` is placed at the centre of mass of rod the TIME period becomes
`2pisqrt((2L)/(3[g^(2)+((QE)/(M))^(2)]^(1//2)))`
the time period for small oscillation of rod is if rod is uncharged is `2pisqrt((2L)/(3g))`
if the point charge Q is place a the lower edge of the rod the time period becomes `2pisqrt((2L)/(3[g^(2)+((QE)/(M))^(2)]^(1//2)))`
if the charge Q is uniformly distributed over the rod the time period
becomes `2pisqrt((2L)/(3[g^(2)+((QE)/(M))^(2)]^(1//2)))`

Solution :
(a). `T=2pisqrt((T)/(Mgd))=sqrt((2L)/(3g))`
(b). `g_(eff)=sqrt(g^(2)+((QE)/(M))^(2)),T=sqrt((I)/(MG_(eff)d))`
Discussion
37408.

The value of angle r in figure below is (##AAK_MCP_36_NEET_PHY_E36_017_Q01.png" width="80%">

Answer»

`r=sin^-1 (1/2)`
`r=sin^-1 (sqrt3/2)`
`r=sin^-1 (8/15)`
`r=sin^-1 (4/15)`

ANSWER :C
Discussion
37409.

The magnetic flux through a circuit of resistance R changes by an amount Adg in time At. The total quantity of electric charge Q, which is passing during this time through any point of the circuit is given by

Answer»

`Q = (Deltaphi_(B))/(DELTAT)`
`Q=(Deltaphi_(B))/(Deltat).R`
`Q=-(Deltaphi_B))/(Deltat).1/R`
`Q=-(Deltaphi_(B))/R`

ANSWER :A::B::D
Discussion
37410.

A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire

Answer»

Solution :`4 XX 10^(-6) ` , VERTICAL up
Discussion
37411.

Obtain the equation of resistivity of metal .

Answer»

Solution :`rArr ` Due to electric field there is unidirectional FLO of charge through cross-section normal t electric field`vec(E)` .

`rArr` Consider plance cross-section A inside conductor. Here `vec(A)` and `vec(E)` are PARALLEL.
`rArr` Due to drift in `Delta` t time interval, electrons RESIDING in`|v_(d) |Delta t` length will be passing through cross-section.
`rArr` Let number density of free electron be n (PER `m^(3)` ).
`rArr` Number of electron passing through areaA in `Delta`t time interval will be N = `nA|v_(d)|Delta`t.
`rArr` If charge of one electron be (- e), then in At time charge passing in area A,
q = - nAe `|v_(d)|Delta` t
`THEREFORE` Charge passing in direction of electric field ,
`(E)/(Delta Q) = + ` nAe `|v_(d)| Delta t `
`I = (Delta Q)/(Delta t) = "ne" Av_(d) "" `...(1)
`rArr` (But `"" v_(d) = (e|E|tau)/(m) `
I ` = "neA" [ (e |E| tau)/(m) ] `
I = `("ne"^(2) A|vec(E)| tau)/(m)`
`|vec(j)| = (I)/(A) = ("ne"^(2) A|vec(E)|tau)/(m) `
Direction of J and `vec(E)` is same hence, it can be considered as scalar,
`j = ("ne"^(2))/(m) tau `E
Comparing with equation obtained by Ohm.s law, (j = `sigma` E)
`sigma E = ("ne"^(2) tau E)/(m)`
`sigma= (1)/(rho)`
`(1)/(rho) = ("ne"^(2) tau)/(m)`
`therefore rho = (m)/("ne"^(2) tau)`
Which represent equation of resistivity of metal (conductor).
Discussion
37412.

A hollow spherre is released from rest on a rough inclined plane as shown in the figure. Find the velocity of point of contact as a function of time. ( m = mass of hollow sphere, R = radius of sphere )

Answer»

2t
4t
6t
8t

Answer :A
Discussion
37413.

A source S_(1) produces 10^(15) photon every second having wavelength of 5000Å .Another source S_(2) produce 1.02xx10^(15) photon every second with wavelength 5100 Å product [Power of S_(1)]xx[Power of S_(2)]=….

Answer»

`1.00`
`1.02`
`1.04`
`0.98`

Solution :Energy produced every second by `S_(1)` (power)
`P_(1)=n_(1)(HC)/(lambda_(1))`
Energy produced every second by `S_(2)` (Power)
`P_(2)=n_(2)(hc)/(lambda_(2))`
`THEREFORE (P_(2))/(P_(1))=(n_(2))/(n_(1))xx(lambda_(1))/(lambda_(2))`
`=(1.02xx10^(15))/(10^(15))xx(5000)/(5100)=1.0`
Discussion
37414.

A , B and C are three points in a uniform electric field. The electric potential is

Answer»

a) MAXIMUM at A
b) maximum at B
c) maximum at C
d) same at all the three POINTS A, B and C

Solution :The POTENTIAL decreases in the direction of the FIELD. THEREFORE `V_(B) gt V_(C) gt C_(A)`.
Discussion
37415.

If the magnitude of the vector product is sqrt(3) times the magnitude of the scalar product, the angle between the two vectors is :

Answer»

`pi/2`
`pi/6`
`pi/3`
`pi/4`

SOLUTION :Here `AB=sintheta=sqrt(ABcostheta`
`:. Tantheta=sqrt(3)`
`theta=60^@=pi/3`RAD
Discussion
37416.

The following table gives the reactance and rms voltage across the elements of a series RCL circuit : {:("Circuit element","Reactance","Voltage across element"),("Resistor", 2.00xx10^2 Omega, 86V),("Inductor",3.77xx10^2 Omega,162V):} What is the impedance of the circuit ?

Answer»

11 `OMEGA`
349 `Omega`
22 `Omega`
486 `Omega`

ANSWER :B
Discussion
37417.

The following table gives the reactance and rms voltage across the elements of a series RCL circuit : {:("Circuit element","Reactance","Voltage across element"),("Resistor", 2.00xx10^2 Omega, 86V),("Inductor",3.77xx10^2 Omega,162V):} What is the rms current in the circuit?

Answer»

0.25 A
0.50 A
0.43 A
0.86 A

Answer :C
Discussion
37418.

A thin converging lens is placed between a fixed object and a screen. There are two positions of thelens for which a sharp image is formed on the screen. The height of one of the images is 2 cm while the magnification of the other image is 3. What is the height of the object?

Answer»

6cm
9cm
10cm
4cm

Answer :A
Discussion
37419.

The radius of a circular coil is R. The distance on the axis fromthe centre of the coil where the intensity of magnetic field is (1)/sqrt(2) times that at the centre, will be:

Answer»

`x=2R`
`x=3R//2`
`x=R`
`x=R//2`

ANSWER :C
Discussion
37420.

The binding energy of a H-atom, considering an electron moving around a fixed nuclei (proton), is B=-(me^(4))/(8n^(2)epsi_(0)^(2)h^(2))(m=electron mass). If one decides to work in a frame of reference where the electron is at rest, the proton would be moving around it. By similar arguments, the binding energy would be B=-(Me^(4))/(8 n^(2)epsi_(0)^(2)h^(2))M= proton mass) thsi last expression is not correct because.

Answer»

would not be INTEGRAL
Bohr-quantisation applies only to electron
the frame in which the electron is at rest is not inertial
the motion of the proton would not be in circular orbits, even approximately.

Solution :If an electron, performing orbital motion is observed from an ACCELERATED frame of reference (i.e. non inertial frame of reference) with an acceleration equal to that of electron, then it will be found at rest by an observer in this fram of reference. But same observer will find protoi in a circular motion. Centripetal force require for this pseudo motion is also IMAGINARY because it does not exist. Here proton does no POSSESS any binding energy due to such imaginary force. Because, to possess bindin energy, centripetal force must be real forci which is exerted in inertial frame of reference
Discussion
37421.

A beam of red light (lambda_(r) = 800 nm) is made up of a stream of photons. In the diagram shown the size of dots represent the photon energy and the spacing represents the spatial distribution of photons. Copy the diagram in your notebook, and just below it draw a similar diagram representing a beam of blue light (lambda_(b) = 400 nm) having same intensity.

Answer»


ANSWER :`(##IJA_PHY_V02_C15_E01_001_A01##)`
Discussion
37422.

Distinguish between nuclear fission and nuclear fusion.

Answer»

SOLUTION :
OR
any other RELEVANT COMPARATIVE DIFFERENCE
Discussion
37423.

If the equation of a progressive wave is given by Y = 4 sin [pi(t/5 -x/9) + pi/6] m

Answer»

9.0 m and 5 sec
18m and 10 sec.
4.5 m and 2.5 sec.
20 m and 36 sec.

Answer :B
Discussion
37424.

In amplitude modulation, sinusoidal carrier frequency used is denoted by omega_( c) and the signal frequency is denoted by omega_(m). The bandwidth (Delta omega_(m)) of the signal is such that Delta omega_(m) lt lt omega_( c). Which of the following frequencies is not contained in the modulated wave?

Answer»

`omega_(m)`
`omega_(c )`
`omega_(m) + omega_(c)`
`OMEGA - omega_(m)`

Solution :The RANGE of frequency of the modulated wave `= omega_(c) pm omega_(m)" " because" " omega_(c) gt gt Delta omega_(m)`, the frequency `omega_(m)` will not be contained in the modulated wave.
`therefore ` The OPTION A is CORRECT.
Discussion
37425.

Yellow light is used in a single slit diffraction experiment with a slit of width 0.6 mm. If yellow light is replaced by X-rays, then the observed pattern will reveal:

Answer»

that the CENTRAL MAXIMUM is narrower
more NUMBER of fringes
less number of fringes
no DIFFRACTION pattern

Answer :A
Discussion
37426.

Are we safer inside a house than under a tree during lightening?

Answer»

Solution :Yes, we are safer inside the HOUSE than under a TREE during LIGHTENING.
Discussion
37427.

The radius of ""_(29)Cu^(64) nucleus in Fermi is : ("given "R_(0)=1.2 xx 10^(-15)m)

Answer»

9.6
4.8
1.2
7.7

Solution :`R=R_(0) A^(1//3) =1.2 xx 10^(-15) xx (64)^(1//3)`
`=4.8 xx 10^(-15) m`
`=4.8" FERMI"`
Discussion
37428.

The capacity of a vessel is 31. It contains 6g O_2,8g N_2 and 5g CO_2 mixture at 27^@C. If R = 8.31 J/mol K, then the pressure in the vessel in N/m2 will be (approx.)

Answer»

`5 XX 10^5 `
`5 xx 10^4`
`1 xx 10^6`
`1 xx 10^5`

ANSWER :A
Discussion
37429.

Two charged capacitors have their outer plates fixed and inner plates connected by a spring of force constant 'K'. The charge on each capacitor is q. find the extension in the spring at equilibrium

Answer»

`(Q^(2))/(2 A epsilon_(0) K)`
`(q^(2))/(4 A epsilon_(0)K)`
`(q^(2))/(A epsilon_(0) K)`
zero

Answer :A
Discussion
37430.

A star is moving towards the earth with a speed of 9.0 xx10^(6) ms^(-1) . If the wavelength of a particularspectral line emitted by it si 6000 Å , then find the apparent wavelength.

Answer»


ANSWER :`5820Å`
Discussion
37431.

A cell of 1.5V is connected across an inductor of 2mH in series with a 2 Omegaresistor What is the rate of growth of current immediately after the cell is switched on.

Answer»

Solution :`E = L(DI)/(dt)+IR ` , Therefore,`(dI)/(dt) = (E-IR)/(L)`
E=1.5 VOLT, `R=2Omega , L=2mH = 2xx10^(-3)`
When the CELL is switched on, I = 0
Hence `(dI)/(dt) = (1.5)/(2 xx 10^(-3)) As^(-1) = 750 As^(-1)`
Discussion
37432.

Proj.j. Prakash asked Vijit whether the average energy density of the electric field and magnetic field are equal or not ? Viji said ''yes''. Justify the answer.

Answer»

Solution :Velocity, `C=(1)/(SQRT(mu_(0)epsilon_(0)))` and `B_(0)=(E_(0))/(c )`
Amplitude of oscillating electric field `= E_(0)`
Amplitude of oscillating MAGNETIC field `= B_(0)`
Average energy density in E field `= (1)/(2)epsilon_(0)E_(0)^(2)`
Average energy density in B field `= (1)/(2mu_(0))B_(0)^(2)`
`((1)/(2mu_(0)))B_(0)^(2)=(1)/(2mu_(0))(E_(0)^(2))/(c^(2))=((1)/(2mu_(0)))mu_(0)epsilon_(0)E^(2)=(1)/(2)epsilon_(0)E^(2)`
`therefore V_(B)=V_(E )`
HENCE the proof.
Discussion
37433.

Calculate the energy released by fission from 2 gm of ""_(92)U^(235) in KWH. Given that the energy released per fission is 200 Mev.

Answer»

Solution :No. of atoms in 1 GM of
`""_(92)U^(235) = ("Avagadro number")/("mass number") = (6.023xx10^(23))/(235)`
Energy released per fission = 200 MEV = `200xx10^(6)xx1.6 xx10^(-19)J`
Total energy released per gm,
`E=(6.023xx10^(23))/235xx200xx10^(6)xx1.6 xx10^(-19)J`
`=(6.023xx200xx1.6)/(235xx36xx10^5)xx10^(10)KWH = 0.2278xx10^5` KWH
Total energy released from 2 gm of `""_(92)U^(235)` is `0.4556xx10^5` KWH
Discussion
37434.

A packet is released from a satellite by simply detaching it from the outer wall of the satellite. What will happen to the packet:

Answer»

it will CONTINUE moving along with the SATELLITE in the same orbit with same velocity.
it will fall to EARTH.
the packet GOES to the space and is lost.
it continues moving along the satellite with half the velocity.

Solution :When packet is released from the satellite then it will continue moving along with the satellite in the same orbit with same velocity.
THUS correct choice is (a).
Discussion
37435.

In a liquid medium of dielectric constant K and of specific gravity 2, two identically charged spheres are suspended from a fixed point by threads of equal lengths. The angle between them is 90^(@). In another medium of unknown dielectric constant K^(1), and specific gravity 4, the angle between them becomes 120^(@). If density of material of spheres is 8gm/cc then find K^(1).

Answer»

SOLUTION :`F= W Tan THETA`
(i) `(1)/(4pi in_(0))(q^(2))/(K(2l^(2)))= mg (1-(2)/(8)) Tan 45^(@)`
(II) `(1)/(4pi in_(0))(q^(2))/(K^(1)(3l^(2)))=mg (1-(4)/(8))Tan 60^(@)`
(iii) gives `K^(1) = (K)/(sqrt3)`
Discussion
37436.

Draw suitable graphs to show the variation of photoelectric current with collector plate potential for (i) a fixed frequency but different intensities I_(1) gt I_(2) gt I_(3) of radiation. (ii) a fixed intensity but different frequencies v_(1) gt v_(2) gt v_(3) of radiation.

Answer»

Solution :Graph showing variation of photoelectric CURRENT `i` with collector PLATE potential V for
(i) a fixed frequency but DIFFERENT intensities of radiation are shown in figure (a), and
(ii) a fixed INTENSITY but different frequencies are shown in figure (b).
Discussion
37437.

When electromagnetic waves enter the ionised layer of ionosphere , then the relative permittivityi.e., dielectric constant of the ionised layer

Answer»

does not change
APPEARS to INCREASE
appears to decrease
SOMETIMES appears to increase and sometimes to decrease

Answer :C
Discussion
37438.

A string when stretched with a weight of 9 kg weigth produces a note of frequency 256. Calculate the weight to produces an octave of the note.

Answer»

36 kg wt
9/4 kg wt
18 kg wt
4 kg wt.

Solution :For stretched string v = `(1)/(2l ) sqrt((T)/(m)) rArr v prop sqrt(T)` .
one OCTANE higher means to double the frequency.
`THEREFORE (v_(2))/(v_(1)) = sqrt((T_(2))/(T_(1))) "" rArr "" (2 xx 256)/(256) = sqrt((T)/(9 "kg wt"))`
`therefore T_(2) = 36 ` kg wt.
Hence correct choice is (a).
Discussion
37439.

If the magnitude of the vector product is sqrt3 times the magnitude of the scalar product, The angle between the two vectors is :

Answer»

`pi/2`
`pi/4`
`pi/3`
`pi/6`

ANSWER :C
Discussion
37440.

Initially switch S is opened and energy stored between the plates of capacitor is E. Now the switch S is closed. Work done by battery after the switch S is closed is W. Find (2E)/W.

Answer»


Solution :`E=1/2(C/2)V^(2) Q_(i)=(CV)/2 Q_(F)=(2CV)/3`
`Q_(f)-Q_(i)=(2CV)/3-(CV)/2=(CV)/6`
`E/W=(CV^(2)//4)/(CV^(2)//5)=3/2 implies(2E)/W=3`
Discussion
37441.

A magnet suspended at30^@ with magnetic meridian makes an angle of45^@ with the horizontal . What shall be the actual value of the angle of dip ?

Answer»

Solution :Here , `theta = 30^@`
Apparent value of DIP ,` delta_1 = 45^@`
Actual value of dip ` delta=?`
If H is horizontal component of earth.s magnetic fieldin the MAGNETICMERIDIAN , then `tan delta=(V)/(H)`
LET `H_1` be component of H at ` 30^@` to magnetic meridian , then ` tan delta_1 = (V)/(H_1) = (V)/(H cos theta ) = ( tan delta)/( cos theta )`
` or tan delta = tan delta_1xx cos theta =tan 45^@ xx cos 30^@`
` = 1 xx (sqrt(3))/(2) = (1.732)/(2) = 0.866`
Discussion
37442.

Draw ouput waveform of a half wave rectifer.

Answer»

SOLUTION :
Discussion
37443.

Assuming the radius of a nucleus to be equal to R= 0.13 root(3)(A) pm, where A is its mass number, evalulate the density of nuclei and the number of nucleons per unit volume of the nucleus.

Answer»

Solution :This problem has misprint. Actually the radius `R` of a nucleus is given by
`R=1.3root(3)(A)FM`
where `fm= 10^(-15)m`
Then the number of nucleous per unit VOLUME is
`(A)/((4 pi)/(3)R^(3))=(3)/(4PI)XX(1.3)^(-3)xx10^(+39)CM^(-3)= 1.09xx10^(38)`per cc
The corresponding mass density is
`(1.09xx10^(38)xx"mass of nucleon") per c c =1.82xx10^(11)kg//c c`
Discussion
37444.

Correct mathc is :

Answer»

(A-S),(B-Q),(C-P),(D-R)
(A-P),(B-R),(C-Q),(D-S)
(A-S),(B-P),(C-Q),(D-R)
(A-R),(B-S),(C-Q),(D-P)

ANSWER :C
Discussion
37445.

In Searle's method for finding conductivity the temperature gradient along the bar is :

Answer»

greater near the hot end
greater near the COLD end
the same at all POINTS
INCREASES as we go from hot end to the cold end.

Solution :In steady state temperature GRADIENT is same at all points along the rod.
Hence correct choice is (C ).
Discussion
37446.

What is AND gate ? Draw its truth table.

Answer»

Solution :AND gate is a LOGIC gate having TWO (or ,more) inputs and one OUTPUT which is AVAILABLE only when all inputs are available.
Discussion
37447.

How does a current loop behave like a magnetic dipole? Draw the magnetic field lines for a current loop to support your answer.

Answer»

Solution :When a current is passed through a closed LOOP , a magnetic field is produced along the axis of the loop and it behaves like a magnetic dipole of moment m = IA. On looking through the axis, if current flows clockwise that FACE will be the south POLE and the other face will be the NORTH pole.
Discussion
37448.

The de-Broglie wavelength of an electron in the first Bohr orbit is equal to

Answer»

the circumference of FIRST ORBIT
(1/2) `XX` (circumference of first orbit )
(1/4) `xx` (circumference of first orbit )
(3/4) `xx` (the circumference of first orbit )

ANSWER :B
Discussion
37449.

The total intensity of the magnetic field of the earth at equator is 6.5 unit. What is its value a pole ?

Answer»

2
4.5
6.5
0

Solution :At MAGNETIC POLE,
`B_V = B SIN PHI = B sin 90^(@) = B = 6.5` UNIT.
`therefore B_(V) = B therefore B_(V) = 6.5` Unit.
Discussion
37450.

A point is situated at certain distance along a line making an angle of 30^@ with the magnetic induction at that point will be :

Answer»

`40^@54'`
`40^@45'`
`40^@32'`
`40^@44'`

Answer :A
Discussion