Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

28701.

The molal freezing point constant of water is -1.86 K molality^(-1). If 171g of cane sugar (C_12H_22O_11) are dissolved in 500 g of water, the solution will freeze at:

Answer»

`-1.86^@C`
`1.86^@C`
`-3.92^@C`
`2.42^@C`

ANSWER :A
Discussion
28702.

The main source of bromine is

Answer»

SILVER BROMIDE ore
sea-water
the Frasch process
phosphate rock

Answer :B
Discussion
28703.

The molar conductivity of the complex CoCl_(3).4NH_(3).2H_(2)O is found to be same as that of 3:1 electrolyte. What is the structural formula. Name and number of geometrical isomer of the complex.

Answer»

SOLUTION :As coordination number of Co is 6 and complex should be `A_(3)B`or`AB_(3)` type, formula is`[Co(NH_(3))_(4)(H_(2)O)_(2)]Cl_(3)`.
Name: Tetraaminediaqua cobalt(III) chloride
GEOMETRICAL isomer: 2(cis and trans)
Discussion
28704.

The molar conductivity of NH_(4)Cl at infinite dilution is 149.7" S "cm^(2) and the ionic conductivities of OH^(-) and Cl^(-) and are 198 and 96.3 S cm^(2) respectively. Calculate the molar conductivity of NH_(4)OH at this dilution.

Answer»


Solution :`wedge_(m)^(@)(NH_(4)OH)=lamda_(m)^(@)(NH_(4)Cl)-lamda_(m)^(@)(Cl^(-))+lamda_(m)^(@)(OH^(-))`
Discussion
28705.

The molar elevation constant for water is 0.52^(@). The elevation caused in the boiling point of water by dissolving 0.25 mole of a non-volatile solute in 250 g of water will be

Answer»

`0.52^(@)C`
`0.052^(@)C`
`5.2^(@)C`
`52^(@)C`

SOLUTION :MOLALITY of solution `=(0.25)/(250)xx1000=1`
`DeltaT_(B)=K_(f)xx m = 0.52xx1=0.52^(@)C`
Discussion
28706.

The main role of oil and fats as constituents in our foods is to:

Answer»

ACT as stored source of energy
To meet IMMEDIATE energy NEEDS of body
To catalyse BIOCHEMICAL process
Form the structural material of tissues

Answer :B
Discussion
28707.

The molar conductivity of the complex CoCl_(3).4NH_(3).2H_(2)O is found to be same as that of 3 : 1 electrolyte. What is the structural formula of the compelx ?

Answer»

Solution :The complex should be of the type `A_(3)B or AB_(3)`. As coordination NUMBER of Co is 6, hence its structure formula will be `[Co(NH_(3))_(4)(H_(2)O)_(2)]Cl_(3)`.
Discussion
28708.

The molar conductivity of solution of a weak acid HX (0.01 M)is ten times smaller than the molar conductivity of a solution of a weak. acid HY (0.1 M). If lambda_(x^(-))^(@) =lambda_(y^(-))^(@), the difference in their pK_(a) values, {pK_(a)(HX) - pK_(a)(HY)} is ..... . (Consider degree of dissociation of both acids to be lt lt 1.

Answer»


Solution :`(Lambda_(HX))/(Lambda_(HY)) = (1)/(10) = (alpha_(HX)//Lambda_(HX)^(@))/(alpha_(HY)//Lambda_(HY)^(@)) because alpha = (Lambda_(c))/(Lambda^(@))`
As`OVERSET(@)(lambda)_(X^(-)) = overset(@)(lambda)_(y^(-)), overset(@)(Lambda)_(HX) therefore (alpha_(HX))/(alpha_(HY)) = (1)/(10)`
`((K_(a))_(HX))/((K_(a))_(HY)) = (0.01 alpha_(HX)^(2))/(0.1 alpha_(HX)^(2))`
Discussion
28709.

The molar conductivity of KCl solutions at different concentrations at 298K are given below: Show that a plot between Lamda_(m) and c^((1//2)) is a straight line. Determine the values of Lamda_(m)^(@) and A for KCl.

Answer»

Solution :Taking the square root of concentration, we obtain:

Graph of `lamda_(m)=sqrt(c) ` vs `c^(1//2)` is as GIVEN below:

It is nearly a straight line.
A=slope=-87.46 S `cm^(2)mol^(-1)("mol "L^(-1))^(1//2)`
From the intercept `(c^(1//2)=0)`, we find that
`Lamda_(m)^(@)=150.0" S "cm^(2)mol^(-1)`.
Discussion
28710.

The main role of DNA in a living system is

Answer»

It is the structural material of CELL walls
It is an enzyme
It carries the HEREDITARY characteristics of the organism
It participates in CELLULAR respiration 

Answer :C
Discussion
28711.

The molar conductivity of KCl solution at different concentrations at 298K are given below: {:(c//mol" "L^(-1),wedge//S" "cm^(2)mol^(-1),c//mol" "L^(-1),wedge//S" "cm^(2)mol^(-1)),(0.000198,148.61,0.000521,147.81),(0.000309,148.29,0.000989,147.09):} Show that the plot between wedge and c^(1//2) is a straight line. determine the values of wedge^(@) and A for KCl.

Answer»

Solution :Taking the SQUARE root of concentration, we obtain
`{:(c^(1//2)(mol" "L^(-1))^(1//2),wedge_(m)//S" "CM^(2)mol^(-1)),(0.01407,148.61),(0.01758,148.29),(0.02283,147.81),(0.03154,147.09):}`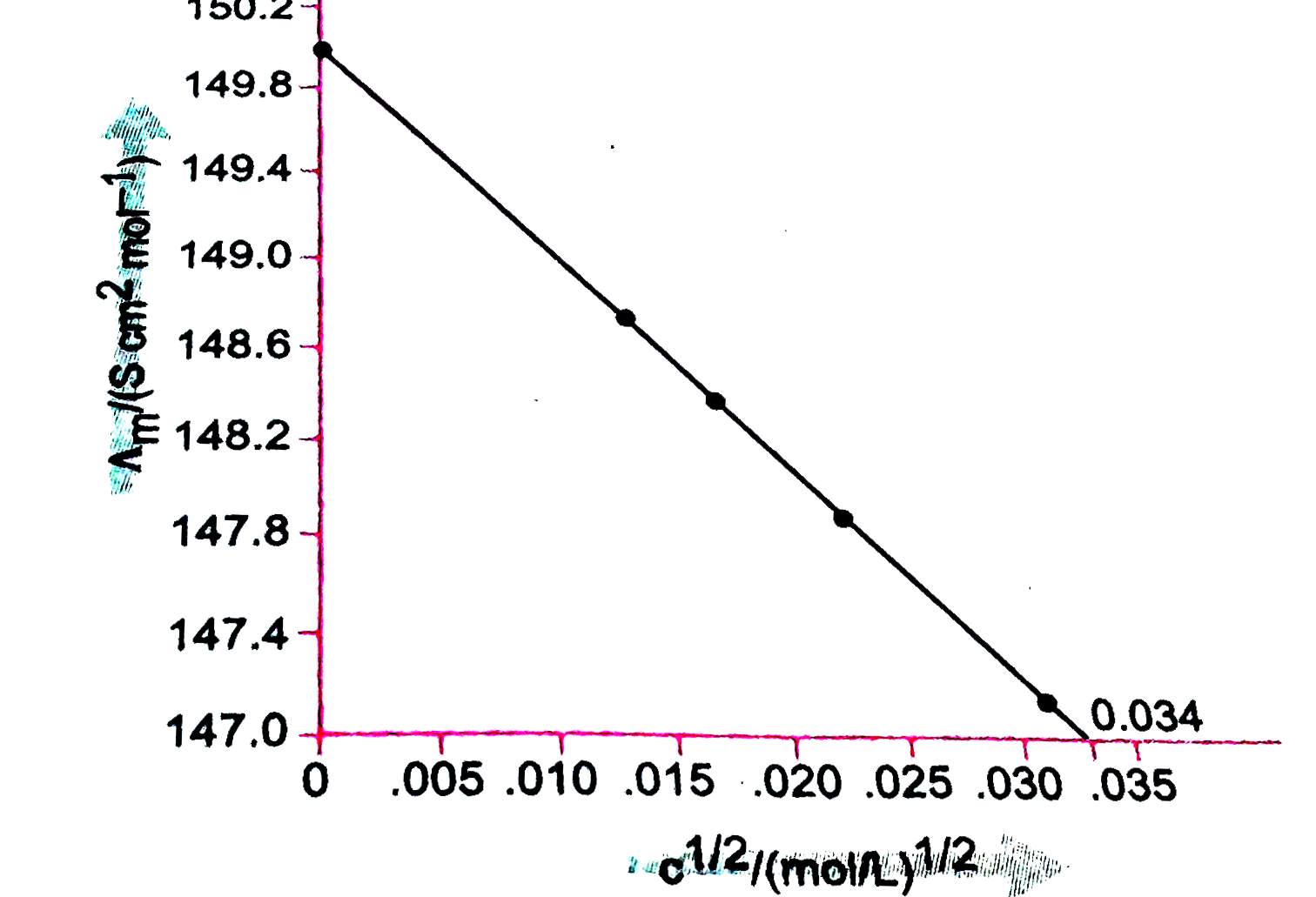

A plot of `wedge_(m)` (y-axis) and `c^(1//2)` (x-axis) is shown in the ADJOINING fig:
It can be seen that it is nearly a straight LINE. from the intercept (i.e., when `c^(1//2)=0`), we find that
`wedge_(m)^(@)=150.0" S "cm^(2)mol^(-1)`
and `A=-"slope"=(Deltay)/(Deltax)=(150.0-147.0)/(0.034)`
`=88.23" S "cm^(2)mol^(-1)//(mol//L^(-1))^(1//2)`.
Discussion
28712.

The molarconductivity of KCl soluitons at difference concentrations at 298 K are given below : {:("c/mol"L^(-1) ,^^_(m)//S cm^(2) " mol"^(-1)),(0.000198,148.61),(0.000309,148.29),(0.000521,147.81),(0.000989,147.09):} Show that a plot betweenE_(m) and c^(1//2) isa straightline . Determie the values of E_(m)^(@) and Afor KCl.

Answer»

Solution :Taking the square root of concentration we obtain:
`{:(c^(1//2)"/"(molL^(-1))^(1//2) ,^^_(m)//S cm^(2) " MOL"^(-1)),(0.01407,148.61),(0.01758,148.29),(0.02283,147.81),(0.03145,147.09):}`
A plotof `^^_(m)` (y - axis ) and `c^(1//2)` (x-axis ) is shownin (fig 3.7)
It can be seen that isnearly a STRAIGHTLINE . From the intercept `(c^(1//2) = 0)`
we find that `E_(m)^(@) = 150.0 S cm^(2) mol^(-1)` andA = - Slope `=87.46 S cm^(2) mol^(-1)// (mol//L^(-1))^(1//2)`
Discussion
28713.

The main reason that SiCl_4 is easily hydrolysed as compared to C Cl_4is that

Answer»

`SI - CL` bond is WEAKER than C - Cl bond
`SiCl_4` can form hydrogen bonds
`SiCl_4` can form hydrogen bonds
`Si` can extend its coordination number beyond four.

Solution :Silicon has GOT vacant .d. orbital but CARBON doesn.t have that. Silicon, also has got larger size than carbon. Hence, silicon can have extended valency rather extanded coordination number.
Discussion
28714.

The molar conductivity of cation and anion of salt BA are 180 and 220 mhos cm^(2) "mol"^(-1) respectively. Themolar conductivity ofsalt BA at infinite dilution is -

Answer»

`90 Omega^(-1)CM^(2)*"mol"^(-1)`
`110Omega^(-1)cm^(2)*"mol"^(-1)`
`200Omega^(-1)cm^(2)*"mol"^(-1)`
`400OMEGA^(-1)cm^(2)*"mol"^(-1)`

ANSWER :A::B::C::D
Discussion
28715.

The main reason that SiCl_(4) is easily hydrolysed as compared to C Cl_(4) is that

Answer»

`Si-Si` bond is weaker
`SiCl_(4)` can form hydrogen bonds
`Si` can EXTEND its coordination NUMBER BEYOND four.
`SiCl_(4)` is ionic.

Answer :C
Discussion
28716.

The molar conductivity of cation and anion of salt BA are 180 AND 220 mhos respectively. The molar conductivity of salt BA at infinite dilution is-

Answer»

90 mhos. `CM^(2). Mol^(-1)`
`110 mhos.cm^(2). Mol^(-1)`
200 mhos. `cm^(2). Mol^(-1)`
400 mhos. `cm^(2). Mol^(-1)`

Answer :D
Discussion
28717.

The main reason for not using a mercury electrolytic cell in NaOH manufacture is that:

Answer»

HG is TOXIC
`Na^+` is discharged at cathode
Hg has a high VAPOUR pressure
Hg is a good CONDUCTOR of electricity

Answer :B
Discussion
28718.

The molar conductivity of acetic acid at infinite dilution is 387omega^(-1)cm^(2)mol^(-1). At the same temperature, but at a concentration of 1 mole in 1000 litres, it is 55 Omega^(-1)cm^(2)mol^(-1). What is the % age dissociation of 0.001 M acetic acid?

Answer»


SOLUTION :1 mol in 1000 litres `=0.001` mol `L^(-1)=0.001M`.
Discussion
28719.

The main reason for the high acidic nature of carbocylic acids : R-COOHhArrR-COO^(-)+H^(+)is

Answer»

greater resonance STABILIZATION of carbocy -lic acid
greter resomance stabilization of carboxy late ION .
greater basic nature of conjugate base , `RCOO^(-)`
EQUAL resonance stabilization of both car boxylic acid and carboxylate ion .

ANSWER :B
Discussion
28720.

The molar conductivity of acetic acid solution at infinite dilution is 390.7 Omega^(-1)cm^(2)mol^(-1). Calculate the moalr conductivity of 0.01M acetic acid solution, given that the dissociation of acetic acid is 1.8xx10^(-5)

Answer»

Solution :`UNDERSET(C(1-alpha))(CH_(3)COOH)hArrunderset(calpha)(CH_(3)COO^(-))+underset(calpha)(H^(+))`
`K_(eq)=calpha^(2)"or"alpha=sqrt((K_(eq))/(c))=(wedge_(m)^(c))/(wedge_(m)^(OO))`
`THEREFORE(wedge_(m)^(c))/(390.7)=sqrt((1.8xx10^(-5))/(0.01))=sqrt(18xx10^(-4))=4.243xx10^(-2)` or `wedge_(m)^(c)=16.57Omega^(-1)cm^(2)`.
Discussion
28721.

The molar conductivity of a solution of a weak acid HX (0.01M) is 10 times smaller than the molar conductivity of a solution of a weak aid HY (0.10M). If lamda_(x^(-))^(0)=lamda_(y-)^(0), the difference in their pK_(a) values, pK_(a)(HX)-pK_(a)(HY), is (consider degree of ionization of both acids to be ltlt1).

Answer»


SOLUTION :`lamda_(x-)^(0)=lamda_(y-)^(0)`
`implieslamda_(H^(+))^(o)+lamda_(X^(-))^(o)=lamda_(H^(+))^(o)+lamda_(Y^(-))^(o)implieslamda_(HX)^(o)=lamda_(HY)^(o)` . . . (i)
Also `(lamda_(m))/(lamda_(m)^(o)=alpha,` so `lamda_(m)(HX)=lamda_(m)^(o)alpha_(1) and lamda_(m)(HY)=lamda_(m)^(o)alpha_(2)`
(where `alpha_(1)` and `alpha_(2)` are degrees of dissociation of HX and HY respectively).
Now, GIVEN that `lamda_(m)(HY)=10lamda_(m)(HZ)implieslamda_(m)^(o)alpha_(2)=10xxlamda_(m)^(o)alpha_(1)`
`alpha_(2)=10alpha_(1)` . . . (ii)
`K_(a)=(Calpha^(2))/(1-alpha)`, but `alpha ltlt 1`, THEREFORE, `K_(a)=Calpha^(2)`
`implies(K_(a)(HX))/(K_(a)(HY))=(0.01alpha_(1)^(2))/(0.1alpha_(2)^(2))=(0.01)/(0.1)xx((1)/(10))^(2)=(1)/(1000)`
`implieslog(K_(a)(HX)-pK_(a)(HY))=-3`
`impliespK_(a)(HX)-pK_(a)(HY)=3`
Discussion
28722.

The main reason for the fact that carboxylic acids can undergo ionization is:

Answer»

ABSENCE of `alpha-H`atom
Resonance STABILIZATION of carboxylate ion
High REACTIVITY of `alpha-H` atom
Hydrogen bonding

Answer :B
Discussion
28723.

The molar conductivity of a solution of a weak acid HX (0.01M) is 10 times smaller than the molar conductivity of a solution of weak acid HY (0.10M). If lamda_(X^(-))^(@)=lamda_(Y^(-))^(@), the difference in their pK_(a) values, pK_(a)(HX)-pK_(a)(HY) is (consider degree of ionization of both acids to be lt lt1).

Answer»


Solution :Suppose `wedge_(m)(HX)` is represented by `wedge_(m_(1))` and `wedge_(m)(HY)` by `wedge_(m_(2))`
Then given that `wedge_(m_(1))=(1)/(10)wedge_(m_(2))`
`HX hArr H^(+)+X^(-),K_(a)=([H^(+)][X^(-)])/([HX])`
Representing `K_a` of HX by `K_(a_(1))`, then as
`K_(a)=Calpha^(2)` and `alpha=(wedge_(m))/(wedge_(m)^(@))`, we have
`K_(a_(1))=C_(1)((wedge_(m_(1)))/(wedge_(m_(1))^(@)))^(2)`. . . (i)
Similarly, `HYhArrH^(+)+Y^(-),K_(a)=([H^(+)][H^(-)])/([HY])`
Representing `K_(a)` of HY by `K_(a_(2))`, we have
`K_(a_(2))=C_(2)((wedge_(m_(2)))/(wedge_(m_(2))^(@)))^(@)`. . . (II)
As `lamda_(X^(-))^(@)=lamda_(Y^(-))^(@),wedge_(HX)^(@)=wedge_(HY)^(@)` or `wedge_(m_(1))^(@)=wedge_(m_(2))^(@)`
From eqns. (i) and (ii)
`(K_(a_(1)))/(K_(a_(2)))=(C_(1))/(C_(2))(wedge_(m_(1)))/(wedge_(m_(2)))^(2)=(0.01)/(0.1)((1)/(10))^(2)` LTBRGT `=0.001=10^(-3)`
or `logK_(a_(1))=logK_(a_(2))=log^(10^(-3))=-3`
or `-logK_(a_(1))-(-logK_(a_(2)))=3`
or `pK_(a_(1))-pK_(a_(2))=3`
Discussion
28724.

The molar conductivity of a 0.5 mol/dm^(3) solution of AgNO_(3) with electrolytic conductivity of 5.76xx10^(-3)" S "cm^(-1) at 298 K is

Answer»

`2.88" S "CM^(2)//mol`
`11.52" S "cm^(2)//mol`
`0.086" S "cm^(2)//mol`
`28.8" S "cm^(2)//mol`

Solution :`wedge_(m)=(kappaxx1000)/("Molarity")`
`=((5.76xx10^(-3)" S "cm^(-1))(1000cm^(3)L^(-1)))/(0.5" mol "L^(-1))`
`=(5.76)/(0.5)=11.52" S "cm^(2)mol^(-1)`.
Discussion
28725.

The main reactions occurring in blast furnace during extraction of iron from heamatite are……………..

Answer»

`Fe_(2)O_(3) +3CO to 2Fe+3CO_(2)`
`FeO +SiO_(2) to FeSiO_(3)`
`Fe_(2)O_(3) +3C to 2Fe+3CO`
`CAO + SiO_(2) to CaSiO_(3)`

Answer :A::D
Discussion
28726.

The molar conductivity of a 0.5 mol dm^(-3) solution of AgNO_3 with electrolytic conductivity of 5.76 xx 10^(-3)S cm^(-1) at 298 K is ………….. .

Answer»

`2.88 S cm^2 mol^(-1)`
`11.52 S cm^2 mol^(-1)`
`0.086 S cm^2 mol^(-1)`
`28.8 S cm^2 mol^(-1)`

SOLUTION :`LAMBDA = k/M xx 10^(-3) mol^(-1) m^(3)`
`= (5.76 xx 10^(-3) S cm^(-1) xx 10^(-3))/(0.5) mol^(-1) m^(3) = (5.76 xx 10^(-3) xx 10^(-3) xx 10^(6))/(0.5) S cm^(-1) mol^(-1) cm^3`
`= 11.52 cm^(2) mol^(-1)`.
Discussion
28727.

The molar conductivity of 0.025 mol L^(-1) methanoic acid is 46.1 S cm^(2)mol^(-1). Calculate its degree of dissociation and dissociation constant. Given lamda^(@)H^(+)=349.6"S "cm^(2)" mole"^(-1) and lamda^(@)(HCO O^(-))=54.6" S "cm^(2)mol^(-1).

Answer»

Solution :(i) Calculation of `lamda-(m)^(@)(HCOOH)`:
`underset("methanoic acid")(HCOOH) to HCOO_((aq))^(-)+H_((aq))^(+)`
`therefore lamda_(m)^(@)(HCOOH)=lamda_(m)^(@)(H^(+))+lamda_(m)^(@)(HCOO^(-))`
`=(349.6+54.6)" S "CM^(2)mol^(-1)`
`=404.2" S "cm^(2)mol^(-1)`
(ii) Calculation for degree of dissociation `(alpha)`:
`alpha=("Molar CONDUCTIVITY")/("LIMITED molar conductivity")|"Where, "lamda_(m)(HCOOH)""=46.1" S "cm^(2)mol^(-1)`
`=(Lamda_(m)(HCOOH))/(Lamda_(m)^(@)(HCOOH))`
`=(46.1" S "cm^(2)mol^(-7))/(404.2" S "cm^(2)mol^(-1))`
`=0.1141`
Percentage of dissociation=`100alpha`
`=100xx0.1141`
`=11.41%`
(iii) Calculation for dissociation constant `K_(a)` :
`therefore K_(a)=(cxxalpha^(2))/((a-alpha))"Where, "c=0.25mol" "L^(-1)`
`=(0.025xx(0.1141)^(2))/((1-0.1141))""alpha=0.1141`
`=(0.025xx(0.1141)^(2))/(0.8859)`
`=0.0003673`
`=3.673xx10^(-4)`.
Discussion
28728.

The main reactions occurring in blast furnace during extraction of iron from haematite are....

Answer»

`Fe_(2)O_3 + 3CO to 2Fe + 3CO_2` 
`FeO + SiO_2 to FeSiO_3`
`Fe_2O_3 + 3C to 2Fe + 3CO` 
`CaO + SiO_2 to CaSiO_3`

SOLUTION :`CO` is reducing agent in extraction of iron and CaO formed by THERMAL DECOMPOSITION of `CaCO_3`, acts as a flux to remove silica IMPURITY as slag
Discussion
28729.

The molar conductivity of 0.025 mol L^(-1) methanoic acid is 46.1 S cm^(2)mol^(-1). Calculate its degree of dissociation and dissociation constant. Given lamda^(@)(H^(+))=349.6" S "cm^(2)mol^(-1) and lamda^(@)(HCO O^(-))=54.6" S "cm^(2)mol^(-1).

Answer»

Solution :`wedge_(m)^(@)(HCOOH)=lamda^(@)(H^(+))+lamda^(@)(HCOO^(-))=349.6+54.6"S "cm^(2)MOL^(-1)=404.2"S "cm^(2)mol^(-1)`
`wedge_(m)^(c)=46.1" S "cm^(2)mol^(1)` (GIVEN)
`thereforealpha=(wedge_(m)^(c))/(wedge_(m)^(0))=(41.1)/(404.2)=0.114`
`{:(,HCOOH,hArr,HCOO^(-),+,H^(+)),("Initial conc.","c mol "L^(-1),,,,),("Conc. at eqm.",c(1-alpha),,calpha,,calpha):}`
`thereforeK_(a)=(calpha.calpha)/(c(1-alpha))=(calpha^(2))/(1-alpha)=(0.025xx(0.114)^(2))/(1-0.114)=3.67xx10^(-4)`
Discussion
28730.

The molar conductivity of a 0.5 mol dm^(-3) solution of AgNO_(3) with electrolytic conductivity of 5.76 times 10^(-3)" S "cm^(-1) at 298 K is

Answer»

2.88 S `CM^(2)MOL^(-1)`
11.52 S `cm^(2)mol^(-1)`
0.086 S `cm^(2)mol^(-1)`
28.8 S `cm^(2)mol^(-1)`

ANSWER :B
Discussion
28731.

The molar conductivity of 0.1 M CH_3COOH solution is 4.6 S cm^2 "mole"^(–1). What is the specific conductivity and resistivity of the solution?

Answer»


ANSWER :A::B::C::D
Discussion
28732.

The main reason as the why C Cl_(4) is not hydrolysed is :

Answer»

ABSENCE of d - ORBITALS of low energy
COVALENT BONDING in `C Cl_(4)`
`C Cl_(4)` is insoluble in WATER.
`C Cl_(4)` has zero dipole moment.

Answer :A
Discussion
28733.

The molar conductivity of 0.05 M BaCl_(2) solution at 25^(@)C is 223 Omega^(-1)"cm"^(2) mol^(-1). What is its conductivity?

Answer»


Solution :Molarconductivity `=^^_(m) =223 Omega^(-1) CM^(2) mol^(-1)`
Concetration= C= 0.05 M `BaCI_(2)`
CONDUCTIVITY = k = ?
`^^_(m) = (k xx 1000)/(C )`
`:. K =(^^_(m) xx C)/(1000)= (223 xx 0.05)/(1000)= 0.01115 Omega^(-1) cm^(-1)`
Discussion
28734.

The molar conductivity of 0.025 mol L^(-1)methanoic acid is 46.1 S cm^(2) mol L^(-1) . Calculate its degree of dissociation and dissociation constant. Given lambda^(@)(H^(+)) = 349.6 S cm^(2) mol^(-1) and lambda^(@) (HCOO^(-)) = 54.6S cm^(2) mol^(-1).

Answer»

Solution :`Lambda_(m)^(@)(HCOOH) = lambda^(@)(H^(+)) + lambda^(@)(HCOO^(-)) = (349.6 + 54.6) S CM^(2) mol^(-1) = 404.2 S cm^(2) mol^(-1)`
`Lambda_(m)^( C) = 46.1 cm^(2) mol^(-1)`
`therefore alpha = (Lambda_(m)^( c))/(Lambda_(m)^(@)) = 46.1/404.2 = 0.114`
To find out dissociation CONSTANT, proceed as follows:
`HCOOH `therefore K_(a) =(Calpha-Calpha)/(C(1-alpha)) =(Calpha^(2))/(1-alpha) =(0.025 xx (0.114)^(2))/(1- 0.114) = 3.67 xx 10^(-4)`
Thus, the dissociation constant `=3.67 xx 10^(-4)`.
Discussion
28735.

Themainreactionsoccuringinblastfurnaceduringextractionofironfromhaematiteare ..........

Answer»

` Fe_ 2 O_3+COto2Fe+3CO _2 `
` FE O+Si O _2toFeSiO _ 2`
`Fe _2 O_3+3C to2Fe +3CO`
`CaO+Si O_ 2 toCaSiO_ 3`

SOLUTION : ` Fe_2 O_3+3 C to2 Fe+3CO`reactiondoesoccurin theblastfurnace attemperaturesabove1123 Kwhen almostall the`Fe _ 2 O _ 3` has alreadybeen reducedto Fe.Therefore,it is notthe mainreaction. Further,` CaCO_3`decomposesaround1123 K TOGIVE CaO. Since,belowthistemperature, FeOhasalreadybeen reducedtoFe,therefore ,`SiO_2`doesnotcombinewithFeOtoform` FeSiO _ 3`SLAG. Thus,themainreactionswhichoccur inthe blastfurnaceare(a) and(d).
Discussion
28736.

The molar conductivity of 0.025 M methanoic acid (HCOOH) is 46.15" S "cm^(2)mol^(-1). Calculate its degree of dissociation and dissociation constant. Given lambda_((H^(+)))^(@)=349.6" S "cm^(2)mol^(-1) and lambda_((HCOO^(-)))^(@)=54.6" S " cm^(2)mol^(-1).

Answer»

Solution :`Lambda_(m)^(@)(HCOOH)=Lambda_(m)^(@)+Lambda_(m)^(@)(HCOO^(-))`
`=349.6+54.6" S cm"^(2)" mol"^(-1)="404.2 S cm"^(2)" mol"^(-1)`
`Lambda_(m)^(@)="46.1 S cm"^(2)" mol"^(-1)` `alpha=(Lambda_(m)^(C ))/(Lambda_(m)^(@))=(46.1)/(404.2)=0.114`
`{:("INITIAL CONC.","C mol L"^(+),0,0),("At equil.",C(1-alpha),Calpha,Calpha):}`
`K_(4)=(Calpha^(2))/(1-alpha)=(0.025xx(0.114)^(2))/(1-0.114)`
`=3.67xx10^(-4)`
Discussion
28737.

The main products of the reaction between C_6 H_5 CHO and formaldehyde in 50% NaOH are

Answer»

Benzyl alcohol and sodium formate
Benzene and HCOONa
CH(3)OH and sodium benzoate
BENZOIN

Solution :Cannziro reaction
`C_(6)H_(5)CHO+HCHO overset(NaOH)to`
`C_(6)H_(5)CH_(2)OH+HCO O Na`
Discussion
28738.

The molarconductivityat zeroconcentrationofNH_(4) CI NaOHand NaCIare respectively 149.7Omega^(-1) cm^(2) mol^(-1) 248.1 Omega^(-1) cm^(2) mol^(-1)and 126.5 Omega^(-1) cm^(2) mol^(-1). Whatis themolarconductivityof NH_(4)OH atzeroconcentration ?

Answer»


SOLUTION :`^^_(o_((NH_(4)C1)) = 149.1 Omega^(-1) CM^(2) mol^(-1)`
`^^_(o_((NAOH)))=248.1 Omega^(-1) cm^(2) mol^(-1)`
`^^_(o_((NaCI)))=126.5 Omega^(-1) cm^(2) mol^(-1)`
By Kohlrausch's law
`^^_(o_((NH_(4)OH)))= lambda_(NH_(4))^(0) + lambda_(OH^(-))^(0)""......(I)`
`^^_(o_((NH_(4)C1)))=lambda_(NH_(4))^(0) + lambda_(C1)^(0)""......(i)`
`^^_(o_((NaOH)))=lambda_(Na^(+))^(0) + lambda_(OH^(-))^(0) ""......(ii)`
`^^_(0_((NaC1)))=lambda_(Na^(+))^(0) + LAMBDA _(C1^(-))^(0)""......(iii)`
Addingequations(i) and (ii) and subtractingequation (iii) wegetequation I.
`:. ^^_(o_((NH_(4)OH))) = ^^_(o_((NH_(4)C1))) + ^^_(0_((NaOH))) ^(-) ^^_(0_((NaC1)))`
`=149.7 + 248 .1- 126. 5`
`=271.3 Omega^(-1)cm^(2) mol^(-1)`
Discussion
28739.

The main product X formed in the following reaction is

Answer»




ANSWER :B
Discussion
28740.

The molar conductivities ofwedge_(NaOAc)^(@) and wedge_(HCl)^(@) at infinite dilution in water at 25^(@)Care 91.0 and 426.2 S cm^(2)//mol respectively. To calculate wedge_(HOAc)^(@), the additional value required is :

Answer»

`wedge_(H_(2)O)^(@)`
`wedge_(KCL)^(@)`
`wedge_(NaOH)^(@)`
`wedge_(NACL)^(@)`

Solution :According to Kohlrausch's LAW:
`Lambda_(CH_3COOH)^(0)=Lambda_(CH_3COONa)^(0)+Lambda_(HCL)^(0)-Lambda_(NaCl)^(0)`
Discussion
28741.

The molar conductivity (Lambda_(m)) of KCl solutions at different concentrations at 298 K is plotted as shown in the figure below: Determine the value of Lambda_(m)^(@) and A for KCl.

Answer»

Solution :On extrapolating the STRAIGHT line to y-axis, it MEETS at `Lambda_(m) = 150 S cm^(2) MOL^(-1)`
`Lambda_(m)^(@) = 150 S cm^(2) mol^(-1)`
A=- SLOPE, Taking points (1) and (2)
`A = (-(148.2-149.1) S cm^(2) mol^(-1))/((0.02 - 0.01)(mol L^(-1))^(1//2)) = 90 S cm^(3) mol^(-1)//(mol L^(-1))^(2)`
Discussion
28742.

The main product when n-butane reacts with Br_(2) at 130^(@)C is:

Answer»

`CH_(3)CH(Br)-CH_(2)CH_(3)`
`CH_(3)CH_(2)CH_(2)CH_(2)Br`
`(CH_(3))_(3)CBR`
None of these

Solution :Secondary H atom is abstracted more EASILY than primary H atom with bromine.
Discussion
28743.

The molar conductivity is maximum for the solution of concentration………………. .

Answer»

`0.001 m`
`0.005 m`
`0.002 m`
`0.004 m`

Solution :MOLAR CONDUCTANCE `PROP 1/("molarity")`
Discussion
28744.

The main product of the reaction CH_(3)CONH_(2)+NaOBr rarr ........ Is

Answer»

`CH_(3)Br`
`CH_(4)`
`CH_(3)OBR`
`CH_(3)NH_(2)`

Solution :`CH_(3)CONH_(2)+NAOBR rarr CH_(3)NH_(3)+NaBr+CO_(2)`
Discussion
28745.

The molar conductivities of H^(+) and HCOO^(-) ions at infinite dilution are 34.7 and 5.4 mSm^(2) " mol"^(-1) respectively. The molar conductivity of 0.25 M HCOOH is 4.0 mSm^(2) mol^(-1). Then pK_(a) of formic acid is

Answer»

3.6
4.2
4.8
1.8

Solution :`ALPHA = (^^_M)/(^^_(M)^(0)) = (4)/(34.6 + 5.4) = (4)/(210) = 0.1 , K_a = C alpha^(2) = 0.025 XX (0.1)^(2) = 25 xx 10^(-5)`
`P^(Ka) = - log(25 xx 10^(-5)) = 5 - log 5^(2) = 5 = 2 log 5 = 5 -2 xx 0.7 = 5 - 1.4 = 3.6`
Discussion
28746.

The main product of the reaction of (C_2H_5)_2CHCHOHCH_3 with conc. H_2SO_4 is

Answer»

`(CH_3CH_2)_2CH-CH=CH_2`
`CH_3-CH(C_2H_5)CH=CH-CH_3`
`(C_2H_5)_2C = CH-CH_3`
both 'a' and 'b'

SOLUTION :It is OBTAINED according to SAYTZEFF RULE `(C_2H_5)_2CHCHOHCH_3 underset(-H_2O)overset(conc. H_2SO_4)to (C_2H_5)_2C=CH-CH_3`
Discussion
28747.

The molar conductivities Lambda_(NaOAc)^@ and Lambda_(HCI)^@ at infinite dilution is watter at 25^@C are 91.0 and 426.2 S cm^@ //mol respectively. To calculate Lambda_(HOAc,)^2 the additional value required is:

Answer»

`^^_(H_(2)O)^(@)`
`^^_(KCL)^(@)`
`^^_(NAOH)^(@)`
`^^_(NaCl)^(@)`

ANSWER :D
Discussion
28748.

the main product of the reaction

Answer»

Nitrobenzene
o- dinitrobenzene
m-dinitrobenzene
p-dinitrobenzene

Answer :C
Discussion
28749.

The main product of the given reaction: But-2-ene + chloroform overset(NaOH)underset("Hydrolysis")to is:

Answer»

BUTANOIC acid
2-methylbutanoic acid
2-methylbutanoic acid
butane-1,4-diol

Solution :N//A
Discussion
28750.

The molarconductivites wedge_(NaOAc)^(@) and wedge_(HCI)^(W)at infinitedilutionin water at 25^(@)Care 91.0 and 426.2 cm^(2)//"mol"respecitvely Tocalculatewedge_(HoAc)^(@)the additional valuerequiredis

Answer»

`wedge_(H_(2)O)^(@)`
`wedge_(KCI)^(@)`
`wedge_(NaOH)`
`wedge_(NACI)`

SOLUTION :Accordingto KOHLRAUSCH 'slaw
`wedge_(CH_(3)COOH)^(@)=wedge_(CH_(3)COOH_(-))^(@) +wedge_(H^(+))^(@)`
`wedge_(HCI)^(@)=wedge_(H^(+))^(@) +wedge_(CI_(-))^(@)`
To calculate`wedge_("GOAC")^(@) =wedge_("HCI")+wedge_(NaOAC)^(@)-wedge_(NaCI)^(@)`thusadditoinal valuerequired is `wedge_(NaCI)^(@)`
Discussion