94420 + Interview Questions in Chemistry in Class 12 Page 1840 InterviewSolution

91951.	5g of Nacl is dissolved in 1000g of water. If the density of the resulting solution is 0.997 g per "cc", calculate the molality, molality, normality and mole fraction of the solute.
Answer» Solution :Mole of NaCl `=(5)/(58.5)=0.0854` (mol.wt.of `NaCl=58.5`) By definition : Molality `=("moles")/("wt.of solvent in grams")xx1000` `=(0.0854)/(1000)xx1000=0.0854m` VOLUME of the solution `=("wt in grams")/("density in grams"//"cc")=(1005)/(0.997)"cc"` `=1008mL=1.008` litres Again by definition molarity `=("moles")/("volume of solution in litres")=(0.0854)/(1.008)=0.085M` `:.` normality = `0.085N` (for NaCl, eq.wt.=mol.wt.) Further, `underset(("PER"1000g))("moles of" H_(2)O)=(1000)/(18)=55.55` (Supposing 1mL=1g for water having density `1g//mL`) TOTAL moles = moles of NaCl `+` moles of `H_(2)O` `=0.0854+55.55=55.6409` Mole fraction of NaCl=`("moles of" NaCl)/("total moles")=(0.0854)/(55.6409)` `=1.53xx10^(-3)`

Discussion

91952.	9*65D C of electric current is passed through fused anhydrous magnesium chloride. The magnesium metal thus, obtained is completely converted into a grignard reagents. What is the number of moles of grignard reagent obtained?
Answer» Solution :`MgCl_(2)overset((AQ))(to)MgCl^(2)+(aq)+2Cl^(-)(aq)` `Mg^(2+)(aq)+UNDERSET((2xx96500C))(2e)^(-)toMg(s)` (At cathode) `2xx29500C` of charge deposite MG metal =1mol `965C` of charge deposite Mg metal `=((1mol))/((2xx96500C))xx(965C)=5xx10^(-5)mol` `R-X+underset(1mol)(Mg)("Anhyd. ether")toR-underset(1mol)(MG)-X` `therefore` No of moles of GRIGNARD REAGENT obtained `=5xx10^(-5)`mol.

Discussion

91953.	5g of a sample of bleaching powder is treated with excess acetic acid and KI solution. The liberated I_(2) required 50 mL of N/10 hypo. The % of available chlorine in the sample.
Answer» Solution :MEQ of bleaching POWDER = meq of `Cl_(2) = ` meq of hypo`W/35.5 XX 1000 = 50 xx 1/10` `W_(Cl_(2))` = 0.1775 g `% Cl_(2) = 0.1775 xx 100 = 3.55%`

Discussion

91954.	5g H_(2) is allowed to react with 14 g N_(2) for the following reaction. N_(2)(g)+3H_(2)(g)rarr2NH_(3)(g) What mass of H_(2) will be left unreached at the end of reaction?
Answer» Solution :`N_(2)` OS ,o,otomg reactamt. THUS `14 g N_(2)` will give 17g `NH_(3)` and xg `H_(2)` REMAINS unreacted. Mass before reaction =Mass after reaction `(5+14)=(17+x)` x=2g

Discussion

91955.	96500C electricity is passed through CuSO_(4) the amount of copper precipitated is
Answer» 0.25 mole 0.5mole 1.0mole 2.00mole Solution :`UNDERSET(1"mole")(CU^(2+))+underset(2"Faraday"=2xx96500C)(2e^(-))rarrCu` 2xx96500C deposits 1 mole of COPPER 96500C deposits 0.5 mole of copper.

Discussion

91956.	5f-level is successively filled up in :
Answer» Lanthanides Actinides RARE gases Transition ELEMENTS ANSWER :B

Discussion

91957.	5Br_((aq))+BrO_(aq)^(-)+6H_((aq))^(+)to3Br_(2(aq))+3H_(2)O_(l) in this reaction (Delta[br^(-)])/(Deltat)=4.2xx10^(-3) mol L^(-1)S^(-1) so calculate (Delta[Br_(2)])/(Deltat) i.e. rate of foramtion of Br_(2)
Answer» SOLUTION :`(5)/(3)xx4.2xx10^(-3) mol L^(-1) S^(-1)`

Discussion

91958.	5A to Product In above reaction, half-life period is directly proportional to initial concentration of reactant. The initial rate of reaction is 400 mol lit^(-1)" min"^(-1).
Answer» ANSWER :3

Discussion

91959.	96500 coulombs deposit 107.9 g of Ag from its soluton. If e = 1.6 xx 10^(-19) coulomb, calculate the number of electrons per mole of electrons
Answer» 96500 `1.6 XX 10^(-19)` `6.02 xx 10^(23)` `6.02 xx 10^(-23)` ANSWER :C

Discussion

91960.	96500 Coulomb will deposite "…………………." of metal.
Answer» SOLUTION :ONE GRAM EQUIVALENT MASS

Discussion

91961.	5.85 g of NaCl are dissolved in 90 g of water, the mole fraction of NaCl is :
Answer» 0.1 0.01 0.2 0.0196 Solution :Moles of NACL`=(5.85)/(58.5)=0.1` Moles of water `=(90)/(18)=5` MOLE fraction of NaCl `=(0.1)/(5+0.1)=0.0196`

Discussion

91962.	96500 coulombs corresponds to the charge on how many electrons-
Answer» `1.6 XX 10^(19)` `6.022 xx 10^(20)` `6.022 xx 10^(23)` `6.022 xx 10^(24)` Answer :C

Discussion

91963.	5.85 g of NaCl is dissolved in 90 g water what is the mole fraction of NaCl ?
Answer» SOLUTION :MOLE fraction , X =( 5.85/ 8.5)/(90/ 18)+( 8.85/58.5) = 0.1/6 + 0.1 = 0.02

Discussion

91964.	9.65C of electric current is passed through fused anhydrous magnesium chloride. The magnesium metal thus, obtained is completely converted into a Grignard reagent. The number of moles of the Grignard reagent obtained is
Answer» `5xx10^(-4)` `1xx10^(-4)` `5xx10^(-5)` `1xx10^(-5)` Solution :96500 COULOMBS of electric current deposits 12 g to Mg. 9.65 coulombs of electric current deposits `(9.65)/(96500)=1.2xx10^(-3)` g of Mg `THEREFORE` No. of moles of GRIGNARD reagent obtained `=(1.2xx10^(-3))/(24)=5xx10^(-5)` moles

Discussion

91965.	58.5 g of NaCl and 180 g of glucose were separately dissolved in 1000 mL of water. Identify the correct statement regarding the elevation of boiling point (b.pt.) of the resulting solutions.
Answer» NACL solution will show HIGHER elevation of b.pt. Glucose solution will show higher elevation of b.pt. Both the solutions will show equal elevation of b.pt The b.pt. of elevation will be shown by NEITHER of the solutions. Solution :`Delta TB = i Kbm` For water `rArr 1000 mL = 1000 g` Molality of `NaCl =(w//M.W)/(W(Solvent) xx 1000` `= (58.5 // 58.5)/(1000) xx 1000 =1m` Molality of gulcose `=(180//180)/(1000) xx 1000 =1m` if For `NaCl =2` , i for glucose = 1 `Delta T_b` for `NaCl GT Delta T_b` for glucose

Discussion

91966.	9.65 C of electric current is passed through fused anhydrous magnesium chloride. The magnesium metal thus obtained is completely converted into a Grignard reagent. The number of moles of Grignard reagent formed is :
Answer» `5XX10^(-4)` `1xx10^(-4)` `5XX10^(-5)` `1xx10^(-5)` Solution :(c ) `Mg^(2+)+underset(2F)2e^(-) to underset(1MOL)Mg` `2xx96500" C"` of CHARGE form Mg =1 mol 9.65C of charge form Mg `=((1mol)xx(9.65" C"))/(2xx(96500" C"))=5xx10^(-5)mol` `Mg-=RMgX` MOLES of Grignand reagent formed `=5xx10^(-5)mol`.

Discussion

91967.	58.5 g of NaCl and 180 g of glucose were separately dissolved in 1000 mL of water. Identify the correct statement regarding the elevation of boiling point (b.pt.) of the resulting solutions
Answer» NaCl solution will show higher ELEVATION of b.pt. GLUCOSE solution will show higher elevation of b.pt. Both the soltuions will show equal elevation of b.pt. The b.pt. of elevation will be shown by neither of the solutions Solution :`Delta T_(b) = i K_(b) m` For water `rarr 1000 ML = 1000 G` Molality of `NaCl=(w//M.W.)/("W(SOLVENT)")xx1000` `=(58.5//58.5)/(1000)xx1000=1m` Molality of glucose `=(180//180)/(1000)xx1000=1m` i for NaCl = 2, i for glucose = 1 `Delta T_(b)` for `NaCl gt Delta T_(b)` for glucose

Discussion

91968.	9.65 C of electric current is passed through fused anhydrous MgCl_(2) .The magnesium metal thus obtained is completely converted into a Grignard reagent. The number of moles of Grignard reagent obtained is
Answer» `5 xxl0^(-4)` MOLES `1 xxl0^(-4)` moles `5 xxl0^(5)` moles `1 xxl0^(5)` moles Answer :A

Discussion

91969.	5.85 g of NaCI is dissoloved in water and the solution is made upto 0.5 litre. The molarity of solution is:
Answer» 1 M 2 M 0.1 M `BaCI_(2)` 0.2 M Solution :`"Molarity of solution (M)"=("Mass of NaCI/Molar Mass")/("Volume of solutin in liters")` ` =((5.85g)//(58.5g MOL^(-1)))/((0.5 L))` `=((0.1 mol))/((0.5 L))=0.2 mol L^(-1)=0.2 M`

Discussion

91970.	5.85 g NaCl is dissovled in 1L water. The number of ions of Na^(+) and Cl^(-) in 1 mL of this solution will be:
Answer» `6.02xx10^(19)` `1.2xx10^(22)` `1.2xx10^(20)` `6.02xx10^(20)` Solution :Number of MOLES of NaCl `=("Mass")/("MOLAR mass")=(5.95)/(58.5)=0.1` Number of ions `(Na^(+)+Cl^(-))` in 1L `=2xx01xx6.023xx10^(23)` `=12.046xx10^(22)` Number of ions in 1mL `=(12.046xx10^(22))/(1000)=1.2xx10^(20)`

Discussion

91971.	9.65 C electric current is passed through fused anhydrous magnesium chloride. The magnesium metal thus obtained is completely converted into a Grignard reagent. The number of moles of the grignard reagent obtained is
Answer» `5xx10^(-4)` `1xx10^(-4)` `5xx10^(-5)` `1xx10^(-5)` SOLUTION :`MG^(2+)+2e^(-)toMg` 2F, i.e., `2xx96500C` deposit Mg=1mole `therefore9.65C` will deposit Mg `=(1)/(2xx96500)xx9.65=5xx10^(-5)` MOLE `RX xx MgtoRMgX` 1 mole of Mg forms G.R.=1 mole `therefore5xx10^(-5)` of Mg will FORM G.R. `=5xx10^(-5)` mole.

Discussion

91972.	58 ml of N/5 H_(2)SO_(4) are used to neutralize ammonia given by 1 g of organic compound. Percentage of nitrogen in the compoundis
Answer» `34.3` `82.7` `16.2` `21.6` SOLUTION :`%` of `N = (1.4 XX " Normality of acid" xx " VOLUME of acid")/(" Mass of substance")` `= (1.4 xx 1 xx 58)/(1 xx 5)= 16.2`

Discussion

91973.	965 amp current is passed through molten metal chloride for one minute and 40 seconds during electrolysis. The mass of metal deposited is 9 gm at the cathode. The valency of metal atom (at. wt = 27) is
Answer» 4 3 2 1 Answer :B

Discussion

91974.	9.65 amp current is passed through moltenAlCl_(3) for one minute forty seconds during electrolysis. The mass of Aldeposited is 0.09g at the cathode. What is the valency of Al
Answer» ANSWER :3

Discussion

91975.	._(95)Am^(241) and ._(90)Th^(234) belongs respectively to
Answer» `4n + 4n +1` radioactive disintegration series `4n + 1 and 4n + 2` radioactive disintegration series `4n + 1 and 4n + 3` radioactive disintegration series `4n + 1 and 4n` radioactive disintegration series Solution :In `._(90)Th^(234)` the MASS no. DIVISION by four gives a residue of 1. In `._(90)Th^(234)` the massno. Division by four gives a residue of 2.

Discussion

91976.	5.8 g of non - volatile, non - electrolyte solute was dissolved in 100 g of carbon disuiphide (CS_(2)). The vapour pressure of the solution was found to be 190 mm of Hg. Calculate molar mass of the solute. Given : Vapour of pure CS_(2) is 195 mm of Hg and molar mass of CS_(2) is 76g//mol.
Answer» Solution :MASS of SOLUTE`(W_(B))=5.8 g`. Mass of solvent i.e., `CS_(2)` is `(W_(A))=100g` Vapour pressure of solution `(RHO)=190` mm of Hg. Vapour pressure of pure solvent `(P_(A))=195` mm of Hg Molar mass of pure solvent`CS_(2)(M_(A))=76 gmol^(-1)`. `M_(B)(p_(A)-p)/(p_(A)^(0))=(W_(B)M_(A))/(M_(B)W_(A))` `(195-190)/(195)=(5.8xx76)/(M_(B)xx100)` `(5)/(195)=(5.8xx76)/(M_(B)xx100)` `M_(B)=(5.8xx76xx195)/(5xx100)=1719 gmol^(-1)`

Discussion

91977.	9.5g of MgCl_(2) is dissolved in 100 g of water . The freezing point of the solution is -4.836^(@)C Then .
Answer» Degree of dissociation of `MgCl_(2)` is `80%` The BOILINGPOINT of the solution is `100.96^(@)C` VANT Hoff FACTOR is 2.6 Osmatic pressure of the solution considering molality and molarity are same is 24.63 atm at `27^(@)C`. Answer :A::C

Discussion

91978.	56g of N_(2) ( molar mass = 28) are mixed with 44g of CO_(2) ( molar mass = 44) and the pressure of the resulting gaseous mixture is 3 atm. The partial pressure of N_(2) in the mixture is :
Answer» i. 1 atm ii. 1.5 atm iii. 2 atm iv. 3 atm Solution :Moles of `N_(2) = ( 56)/( 28) =2 ` Moles of `CO_(2) = ( 44)/( 44) = 1 ` Mole fraction of `N_(2) = ( 2)/( 2+1) = ( 2)/(3)` Partial PRESSURE of `N_(2) = ( 2)/(3) xx 3 = 2 atm`

Discussion

91979.	9.5 g of CH_2 FCOOHis dissolved in 500 g of water. The depression in the freezing point observed is 1.0^@C . Calculate the van't Hoff factor and dissociation constant of fluroacetic acid.
Answer» Solution :Given `w_2 = 19.5 , w_1 = 500 g, K_f = 1.86 K kg "mol"^(-1) ,(Delta T_f)_(OBS) = 1.0^@C` ` therefore M_2 `(OBSERVED ) `= (1000K_f w_2)/(w_1 Delta T_f) = (1000 XX 1.86 xx 19.5)/(500 xx 1.0) = 72.54 g "mol"^(-1)` `M_2`(calculated) for `CH_2FCOOH = 14 + 19 + 45 = 78 g "mol"^(-1)` van.t hoff factor (i)` = ((M_2)_(cal))/((M_2)_(obs)) = (78)/(72.54) = 1.0753` Calculation of dissociation constant : suppose degree of dissociation at the given concentration is `alpha` 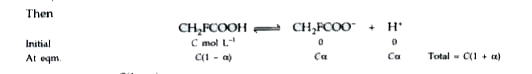` therefore i = (C(1+alpha))/(C ) =1 + alpha` or ` alpha = i-1 = 1.0753 -1=0.0753` Dissociation constant of the ACID is calculated as under : `K_alpha = ([K_2FCOO^(-)][H^+])/([CH_2FCOOH]) =(Calpha.Calpha)/(C(1-alpha)) = (C.alpha^2)/(1- alpha)` Concentration `C = (19.5)/(78) xx 1/500 xx 1000 = 0.5M` ` therefore K_alpha = (C alpha^2)/(1- alpha) = ((0.5)(0.0753)^2)/(1-0.0753) = 3.07 xx 10^(-3)`

Discussion

91980.	56g of gaseous nitrogen and 64g of gaseous sulphur dioxide are mixed together in a 6L vessel. If the total pressure of the mixture is 3 atm, what will be the partial pressure of nitrogen in the mixture ?
Answer» 3 atm 1 atm 1.5 atm 2 atm Answer :D

Discussion

91981.	95% ethyl alcohol can be converted to 100 % ethyl alcohol by the following
Answer» MAGNESIUM chloride Calcium oxide Magnesium phosphate Magnesium sulphate Answer :B

Discussion

91982.	5600 ml of O_(2) is obtained by electrolysis at STP, then how much Ag is obtained by same electricity ? (atomic mass of Ag=108)
Answer» `5.4gm` `10.8gm` `54.0gm` `108.0gm` SOLUTION :`n_(O_(2))=(5600)/(22400)=(1)/(4)` MOL `O_(2)` `(W_(Ag))/(108)xx1=(W_(O_(2)))/(M_(O_(2)))xx4""(2H_(2)O to O_(2)+4H^(+)+4e^(-))` `(W_(Ag))/(108)xx1=(W_(O_(2)))/(M_(O_(2)))xx4` `(W_(Ag))/(108)=(1)/(4)xx4""therefore W_(Ag)=108gm`.

Discussion

91983.	._(92)U^(235) + n rarrfission product + neutron + 3.20 xx 10^(-11) J. The energy released when 1g of ._(92)U^(235) undergoes fission is
Answer» `12.75 xx 10^(8) kJ` `18.60 xx 10^(9) kJ` `8.21 xx 10^(7) kJ` `6.55 xx 10^(6) kJ` Solution :`1g U-235 = (6.023 xx 10^(23))/(235)` ATOMS `:.` ENERGY released `= 3.2 xx 10^(-11) xx (6.023 xx 10^(23))/(235) J` `= 8.21 xx 10^(1) J = 8.2 xx 10^(7) kJ`

Discussion

91984.	._(92)U^(235) belongs to group III B of periodic table. If it loses one alpha-particle, the new element will belong to group
Answer» I B I A III B V B Solution :ELEMENTS 89 to 103 are placed in III GROUP. These are ACTINIDES.

Discussion

91985.	5.6 litres of methane (CH_(4)) gas are ignited in oxygen gas. Calculate the number of moles of CO_(2) formed.
Answer» ANSWER :0.25 MOLE

Discussion

91986.	""_(92)U^(235) belongs IIIB of the periodic table. If it losses one alpha particle, the new element will belong to group
Answer» I B I A III B V B Solution :III B is group 3. On LOSING `alpha`- PARTICLE, the NEW element will be in group 1 i.e. I A.

Discussion

91987.	56 g of nitrogen and 8 g of hydrogen gas are heated in a closed vessel. At equilibrium 34 gof ammonia are present. The equilibrium number of moles of nitrogen, hydrogen and ammonia are respectively
Answer» 1, 2,2 2,2,1 1, 1, 2 2, 1, 2 ANSWER :C

Discussion

91988.	""_(92)U^(235)belong to group IIIB to periodic table. If it loses one alpha particle, the new element will belong to the group
Answer» VB IA IIA IIIB Answer :C

Discussion

91989.	56 g of nitrogen and 8 g of hydrogen gas are heated in a cloed vessel. At equilibrium, 34 g of ammonia are present. The equilibrium number of moles of nitrogen, hydrogen and ammonia are respectively
Answer» 1, 2, 2 2, 2, 1 1, 1, 2 2, 1, 2 Solution :56 g of `N_(2)` = 56/28 = 2 moles, 8 g of `H_(2)` = 8/2 = 4 moles, 34 g of `NH_(3)` = 34/17 = 2 moles. `{:(,N_(2),+,3H_(2),iff,2NH_(3)),("INITIAL","2 moles",,"4 moles",,),("At eqm.","2 - 1 mole",,"4 - 3 moles",,"2 moles"),(,"= 1 mole",,"= 1 mole",,):}`

Discussion

91990.	5.6 g of but-2-ene is taken ina 250 mL round bottom flask. 3.7 g of conc, HCl is added to it and the resultant mixture is stirred till the reaction is complete . The practical yield of the reaction is 50% , Calculate the mass of the product formed.
Answer» 0.35 g 5.6 g 0.35 g 9.25 g Answer :B

Discussion

91991.	""_92^238Uis radioactive and it emits alpha and beta particles to form ""_82^206Pb . Calculate the numberof alpha and betaparticles emitted in this conversion. An ore of ""_92^238Uis found to contain ""_92^238U and""_82^206Pbin the weight ratio of 1:0.1. The half-life period ""_92^238U is 4.5 xx 10^9 years. Calculate the age of the ore.
Answer» SOLUTION :`8, 6, 7.098 XX 10^8 ` YEARS

Discussion

91992.	5.6 g of an organic compound on burning with excess of oxygen gave 17.6g of CO_(2) and 7.2 g H_(2)O. The organic compound is:
Answer» `C_(6)H_(6)` `C_(4)H_(8_` `C_(3)H_(8)` `CH_(3)COOH` Answer :B

Discussion

91993.	._(92)^(238)U emits 8 alpha-particles and 6-beta-particles. The neutron/proton ratio in the product nucleus is
Answer» 60/41 61/40 62/41 61/42 Solution :`._(92)U^(238) underset(-6beta)overset(-8alpha)rarr ._(82)X^(2-6)` Number of protons = 82, Number of neutrons = 124 Neutron/proton RATIO in the PRODUCT nucleus `= (124)/(82) = (62)/(41)`

Discussion

91994.	5.6 g of a steel sample containing sulphur impurity was burnt in oxygen. SO_2 , so produced, was then oxidised to sulphate by H_2O_2solution to which 30 mL of 0.004 M NaOH solution had been added. 22.48 mL of 0.024 M HCl was required to neutralize the base remaining after oxidation reaction. Calculate percentage of S in the given sample of steel.
Answer» Solution :`SO_2 + H_2O_2 + 2OH^(-) = SO_4^(2-) + 2H_2O` m mol of S = MMOL of `SO_2 = 1/2 XX ` m mol of `OH^(-)= (30 xx 0.04) - 22.48 xx 0.024)`

Discussion

91995.	._(92)^(238)U by successive radioactive decay changes to ._(82)^(206)Pb. A sample of uranium ore was analysed and found to contain 1.0g of .^(238)U and 0.1g of .^(206)Pb. Assuming that all .^(206)Pb hasaccumulated due to decay of .^(238)U, find the age of the ore (half life of .^(238)U=4.5xx10^(9) yrs).
Answer» SOLUTION :Number of MOLES of `.^(238)U = (1)/(238)` Number of moles of `.^(206)Pb = (0.1)/(206)` Applying the relationship, `t = (2.303/(lambda) log [1 + (.^(206)Pb)/(.^(238)U)]` `= (2.303)/(0.693) xx 4.5 xx 10^(9) log [1 + ((0.1)/(206))/((1)/(238))] = 7.098 xx 10^(8)` YEARS

Discussion

91996.	5.6 amp
Answer» 7.2 AMP 8.85 amp 11.2 amp Answer :C

Discussion

91997.	""_(92)^(238)U by successive radioactive decay changes to ""_(82)^(206)Pb. A sample of uranium ore was analysed and found to contain 1.0 gm of .^(238)U and 0.1gm of .^(206)Pb. Assuming that all the .^(206)Pb has accumulated due to decay of .^(238)U, find the age of the ore (half-life of .^(238)U=4.5xx10^(9)years).
Answer» ANSWER :`7.098xx10^(8)` YEARS

Discussion

91998.	5.5 mg of nitrogen gas dissolves in 180 g of water at 273 K and one atm pressure due to nitrogen gas.The mole fraction of nitrogen in 180 g of water at 5 atm nitrogen pressure is approximately
Answer» `1XX10^(-6)` `1xx10^(-5)` `1xx10^(-3)` `1xx10^(-4)` Solution :Solubility of a gas `PROP` mole fraction `n_(N_(2))=(5.5xx10^(-3))/(28)=1.96xx10^(-4)` at 1 atm Now,p `prop` mole fraction then at 5 atm, the mole fraction will increase 5 TIMES. HENCE, `5xx1.96xx10^(-4)= 9.8xx10^(-4)~~10xx10^(-4)= 1.0xx10^(-3)`

Discussion

91999.	""_(92)^(238) U is the element of III B group , it undergoes decay as follows , ""_(92) ^(238) U overset(- alpha)(to) A overset(-alpha)(to) B overset(-beta)(to) C Which of the following statements is/are correct ?
Answer» A will be of III B group A will be of 1 B group B will of II A C is the isotope of `""_(92)^(238) U` SOLUTION :`""_(92) U^(238) overset(- (""_(2) He^(4)))(to) ""_(90) TH^(234) overset(- (""_(2) He^(4)))(to) ""80 Ra^(230) overset(- (""_(1) beta^(0)))(to) ""_(89) Z^(230)`

Discussion

92000.	5.39of a mixture of FeSO_(4). 7H_(2)Oand anhydrous ferricsulphaterequires80 mL of 0.125 N permangnatesolution for complete conversion to ferricsulphate. Calculate the individual weights of eachcomponentof the original mixture .
Answer» Solution :FERRUS ulphatepresentin the mixtureto oxidisedto ferricsulphate by permagnate solution . LET the weight of ferrous sulphatebe x gram . m.e of `FeSO_(4).7H_(2)O`= m.e of permagnate solution ` = 0.125 xx 80 = 10 ` ` :. ` eq. of `FeSO_(4) . 7H_(2) O = 10/1000 ""...(EQN . 3)` ` :. ` WT . of `FeSO_(4) .7H_(2)O = eq xx eq.wt ` ` = 10/1000 xx 278` ` = 2.78 g` and wt. of `Fe_(2) (SO_(4))_(3) = (5.39 - 2.78 ) g ` ` = 2.61 g `

Discussion

Explore topic-wise InterviewSolutions in .

5g of Nacl is dissolved in 1000g of water. If the density of the resulting solution is 0.997 g per "cc", calculate the molality, molality, normality and mole fraction of the solute.

9*65D C of electric current is passed through fused anhydrous magnesium chloride. The magnesium metal thus, obtained is completely converted into a grignard reagents. What is the number of moles of grignard reagent obtained?

5g of a sample of bleaching powder is treated with excess acetic acid and KI solution. The liberated I_(2) required 50 mL of N/10 hypo. The % of available chlorine in the sample.

5g H_(2) is allowed to react with 14 g N_(2) for the following reaction. N_(2)(g)+3H_(2)(g)rarr2NH_(3)(g) What mass of H_(2) will be left unreached at the end of reaction?

96500C electricity is passed through CuSO_(4) the amount of copper precipitated is

5f-level is successively filled up in :

5Br_((aq))+BrO_(aq)^(-)+6H_((aq))^(+)to3Br_(2(aq))+3H_(2)O_(l) in this reaction (Delta[br^(-)])/(Deltat)=4.2xx10^(-3) mol L^(-1)S^(-1) so calculate (Delta[Br_(2)])/(Deltat) i.e. rate of foramtion of Br_(2)

5A to Product In above reaction, half-life period is directly proportional to initial concentration of reactant. The initial rate of reaction is 400 mol lit^(-1)" min"^(-1).

96500 coulombs deposit 107.9 g of Ag from its soluton. If e = 1.6 xx 10^(-19) coulomb, calculate the number of electrons per mole of electrons

96500 Coulomb will deposite "…………………." of metal.

5.85 g of NaCl are dissolved in 90 g of water, the mole fraction of NaCl is :

96500 coulombs corresponds to the charge on how many electrons-

5.85 g of NaCl is dissolved in 90 g water what is the mole fraction of NaCl ?

9.65C of electric current is passed through fused anhydrous magnesium chloride. The magnesium metal thus, obtained is completely converted into a Grignard reagent. The number of moles of the Grignard reagent obtained is

58.5 g of NaCl and 180 g of glucose were separately dissolved in 1000 mL of water. Identify the correct statement regarding the elevation of boiling point (b.pt.) of the resulting solutions.

9.65 C of electric current is passed through fused anhydrous magnesium chloride. The magnesium metal thus obtained is completely converted into a Grignard reagent. The number of moles of Grignard reagent formed is :

58.5 g of NaCl and 180 g of glucose were separately dissolved in 1000 mL of water. Identify the correct statement regarding the elevation of boiling point (b.pt.) of the resulting solutions

9.65 C of electric current is passed through fused anhydrous MgCl_(2) .The magnesium metal thus obtained is completely converted into a Grignard reagent. The number of moles of Grignard reagent obtained is

5.85 g of NaCI is dissoloved in water and the solution is made upto 0.5 litre. The molarity of solution is:

5.85 g NaCl is dissovled in 1L water. The number of ions of Na^(+) and Cl^(-) in 1 mL of this solution will be:

9.65 C electric current is passed through fused anhydrous magnesium chloride. The magnesium metal thus obtained is completely converted into a Grignard reagent. The number of moles of the grignard reagent obtained is

58 ml of N/5 H_(2)SO_(4) are used to neutralize ammonia given by 1 g of organic compound. Percentage of nitrogen in the compoundis

965 amp current is passed through molten metal chloride for one minute and 40 seconds during electrolysis. The mass of metal deposited is 9 gm at the cathode. The valency of metal atom (at. wt = 27) is

9.65 amp current is passed through moltenAlCl_(3) for one minute forty seconds during electrolysis. The mass of Aldeposited is 0.09g at the cathode. What is the valency of Al

._(95)Am^(241) and ._(90)Th^(234) belongs respectively to

5.8 g of non - volatile, non - electrolyte solute was dissolved in 100 g of carbon disuiphide (CS_(2)). The vapour pressure of the solution was found to be 190 mm of Hg. Calculate molar mass of the solute. Given : Vapour of pure CS_(2) is 195 mm of Hg and molar mass of CS_(2) is 76g//mol.

9.5g of MgCl_(2) is dissolved in 100 g of water . The freezing point of the solution is -4.836^(@)C Then .

56g of N_(2) ( molar mass = 28) are mixed with 44g of CO_(2) ( molar mass = 44) and the pressure of the resulting gaseous mixture is 3 atm. The partial pressure of N_(2) in the mixture is :

9.5 g of CH_2 FCOOHis dissolved in 500 g of water. The depression in the freezing point observed is 1.0^@C . Calculate the van't Hoff factor and dissociation constant of fluroacetic acid.

56g of gaseous nitrogen and 64g of gaseous sulphur dioxide are mixed together in a 6L vessel. If the total pressure of the mixture is 3 atm, what will be the partial pressure of nitrogen in the mixture ?

95% ethyl alcohol can be converted to 100 % ethyl alcohol by the following

5600 ml of O_(2) is obtained by electrolysis at STP, then how much Ag is obtained by same electricity ? (atomic mass of Ag=108)

._(92)U^(235) + n rarrfission product + neutron + 3.20 xx 10^(-11) J. The energy released when 1g of ._(92)U^(235) undergoes fission is

._(92)U^(235) belongs to group III B of periodic table. If it loses one alpha-particle, the new element will belong to group

5.6 litres of methane (CH_(4)) gas are ignited in oxygen gas. Calculate the number of moles of CO_(2) formed.

""_(92)U^(235) belongs IIIB of the periodic table. If it losses one alpha particle, the new element will belong to group

56 g of nitrogen and 8 g of hydrogen gas are heated in a closed vessel. At equilibrium 34 gof ammonia are present. The equilibrium number of moles of nitrogen, hydrogen and ammonia are respectively

""_(92)U^(235)belong to group IIIB to periodic table. If it loses one alpha particle, the new element will belong to the group

56 g of nitrogen and 8 g of hydrogen gas are heated in a cloed vessel. At equilibrium, 34 g of ammonia are present. The equilibrium number of moles of nitrogen, hydrogen and ammonia are respectively

5.6 g of but-2-ene is taken ina 250 mL round bottom flask. 3.7 g of conc, HCl is added to it and the resultant mixture is stirred till the reaction is complete . The practical yield of the reaction is 50% , Calculate the mass of the product formed.

5.6 g of an organic compound on burning with excess of oxygen gave 17.6g of CO_(2) and 7.2 g H_(2)O. The organic compound is:

._(92)^(238)U emits 8 alpha-particles and 6-beta-particles. The neutron/proton ratio in the product nucleus is

5.6 amp

5.5 mg of nitrogen gas dissolves in 180 g of water at 273 K and one atm pressure due to nitrogen gas.The mole fraction of nitrogen in 180 g of water at 5 atm nitrogen pressure is approximately

""_(92)^(238) U is the element of III B group , it undergoes decay as follows , ""_(92) ^(238) U overset(- alpha)(to) A overset(-alpha)(to) B overset(-beta)(to) C Which of the following statements is/are correct ?

5.39of a mixture of FeSO_(4). 7H_(2)Oand anhydrous ferricsulphaterequires80 mL of 0.125 N permangnatesolution for complete conversion to ferricsulphate. Calculate the individual weights of eachcomponentof the original mixture .